二分类响应变量下判别分析与Logistic回归比较

董小刚, 刘新蕊

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

在日常生活及科学研究中,经常会遇到将问题的结果用类别表示的情况。在研究此分类问题时,最常用的方法是线性判别分析与Logistic回归。这两种方法简单实用,易于计算,应用广泛。两种方法理论基础的差异使得它们各有优势，Logistic回归在给出具体分类的同时,还能描述影响分类结果的因素,而判别分析则仅对样本进行分类。线性判别分析对数据进行了特殊假设，它假设响应变量类间相互独立,同类样本服从多元正态分布,且具有相同的类内协方差阵。

这两种方法都具有很高的实用价值,如张晓东等[1]通过判别分析探讨了肺癌细胞核的有关体视学参数在肺癌诊断分型方面的意义;易尚辉等[2]对因大肠癌而住院的病历按治愈和未愈分两组进行了非条件多因素Logistic回归分析;王浩等[3]基于Logistic回归探讨了进展期胃癌淋巴结的转移规律;张立军等[4]以我国沪市 A 股上市公司为研究对象,利用判别分析研究上市公司财务危机预警;张成虎等[5]基于个人消费信贷数据,建立了个人信用评分的线性判别模型;朱燕波等[6]对 18 805例中国成年人建立Logistic回归，分析了中医体质类型与超重和肥胖的关系;李洪等[7]基于Logistic回归构建了北京市水库湿地演变的驱动因子指标体系;杨秀玮等[8]探讨了Bayes判别分析应用于输卵管妊娠早期诊断中的临床效果。因此,对两种方法的拟合效果进行比较是有意义的。

将研究对象分为两类，称为二分类问题。鉴于二分类问题的代表性和广泛性，文中主要讨论二分类问题，此方法也可以推广到多分类的情况。

1 二分类下的线性判别分析与Logistic回归

线性判别分析(LDA)也称Fisher线性判别,是统计学上一种经典的分析方法,在医学中的患者疾病分级、经济学的市场定位等领域有广泛的应用。

假设R0和R1分别表示两个类别,p维样本数据集X={xi|i=1,2,3,…,n}中属于R0的样本个数为n0,属于R1的样本个数为n1,n0+n1=n。Ω=R0∩R1表示两个总体的并集,包含所有的研究对象。w为一向量,那么x到w上的投影为y=wTx,表示投影到w上的点到原点的距离。

类别i(i=0,1)的类内样本均值

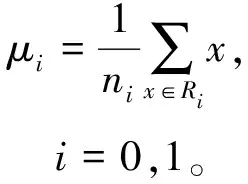
(1)

类别i在投影后的类内均值

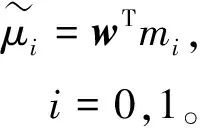
(2)

由式(1)和式(2),投影后的均值即样本中心点的投影,使投影后的两类样本中心点尽量分离的直线定量表示为

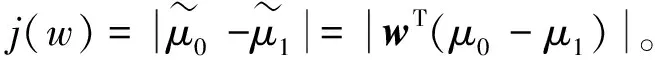
(3)

j(w)越大,分类直线的效果较好,但是两个类别的投影之间很容易有重叠,因此,还需要考虑样本类内点之间的距离够小。投影后,类内点之间的分离程度,即类内方差为

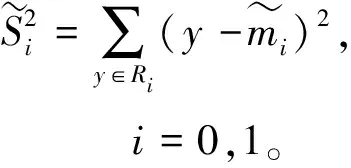
(4)

由式(4)可以看出,该值越大效果越好。因此最终的度量公式为

找到使得J(w)最大的w即可,这就是Fisher在1936年提出的线性判别分析。只有每一类都服从多元正态分布且类间协方差矩阵相同时,才能够得到线性的分界线。

为了得到最优分类,引入后验概率πk，它表示类k(k=0,1)的先验概率,且π0+π1=1。线性判别函数

k=0,1,

是判定规则的等价描述。

Logistic回归模型是广义线性模型的一个特例,是对定性变量建立回归模型时的一种常用方法。与线性判别分析不同,Logistic回归对于数据的分布不做任何假设,并且得到的模型形式也不是线性的。

回归通过x的线性函数对K个类别建立模型,而同时确保它们的和为1,并且都在[0,1]中。该模型具有如下形式

i=1,2,…,K-1。

当K=2时，就是我们要研究的模型,此时的模型形式简单,只要一个线性函数，因此被广泛应用于二分类响应变量下的分类问题。

将Logistic回归模型与线性判别分析的模型进行对比,它们的模型形式较为相似,仅参数估计方法有差异,但线性判别分析要求样本来自多元正态总体,且不同类的协方差阵相同,而Logistic回归对于数据没有任何要求。

2 比较指标

为了直观地比较两种方法,文中选取了4个比较指标,分别为回判错误率、指标B、C、Q。它们从不同方面如预测精度、组间分离程度,展示了两种方法的表现。

回判错误率(CE)是指模型或者判别准则建立后,对原有样本进行分类,在分类结果中判断错误的对象所占百分比，即

式中：n----所有观测个数；

nr----回判错误观测个数。

这是一个简单直观,易于理解的比较指标,然而在实际应用中,它却往往并不敏感,我们能从中得到的信息非常少,因此仅仅利用回判错误率来衡量这两种方法的好坏是不够严谨的[9]。Harrel和Lee[10]提出了三种不同的比较这两种方法判别能力的指标,分别为B、C和Q。这三个指标能够更好、更高效的对两种方法进行对比,提供更多的信息。

指标B以估计值与实际值之差平方的均值来衡量预测结果准确性，计算式为

式中：Pi----观测i的预测分组情况(0或1)；

Yi----实际分组情况(0或1)；

n----总样本容量。

指标B的取值在区间[0,1],当预测结果越准确时,指标B的值越接近于1。

指标C用来判别模型的组间分离能力,计算式为

式中：Pk----线性判别分析和Logistic回归的后验概率Pr(1|Xk)的估计值；

I----示性函数；

n0----判别为0组的观测个数；

n1----判别为1组的观测个数。

指标C的值不受实际分组情况的影响,因此它只是一个表示组间分离情况的指标,并不能衡量预测精度。当组间的分离程度越大时,指标C的值越大,接近于1，当C为0.5时,为一个随机预测模型。

指标Q与B类似,用来衡量预测精度,Q的计算式为

式中：Pi----线性判别分析和Logistic回归的后验概率Pr(1|Xk)的估计值；

Yi----实际分组情况(0或1)；

n----总样本容量。

当预测精度越大时,指标Q的值越接近于1;当指标Q的值为0时,表示模型是随机预测。

3 数值模拟

为了明确两种方法的适用范围,分别在不同的类内均值间距离、解释变量个数、解释变量间相关性、样本容量、类间样本差值、协方差阵下对两种方法进行比较。

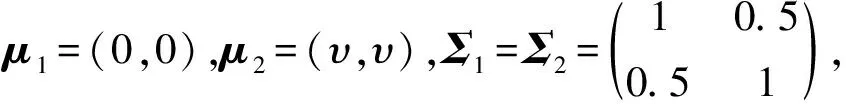
模拟2:G1～N(μ1,Σ1),G2～N(μ2,Σ2),样本容量n1=n2=50,固定μ1为各分量均为0的p维向量,μ2为各分量均为1.5的p维向量,Σ1和Σ2对角线元素为1,其余元素为0.5的p维方阵,分别取p=2,3,4,5。

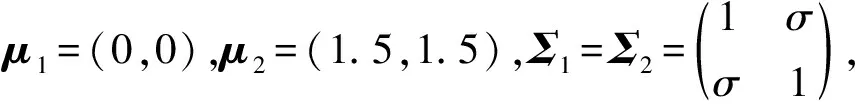
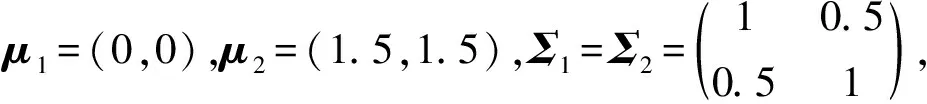
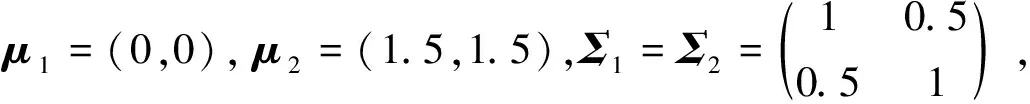
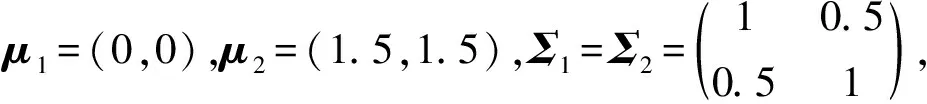
类内均值间距离大小(υ)、解释变量(p)个数、解释变量间相关性(σ)、类样本容量(n)、类样本容量间差距(Δ)及非正态的影响分别见表1～表6。

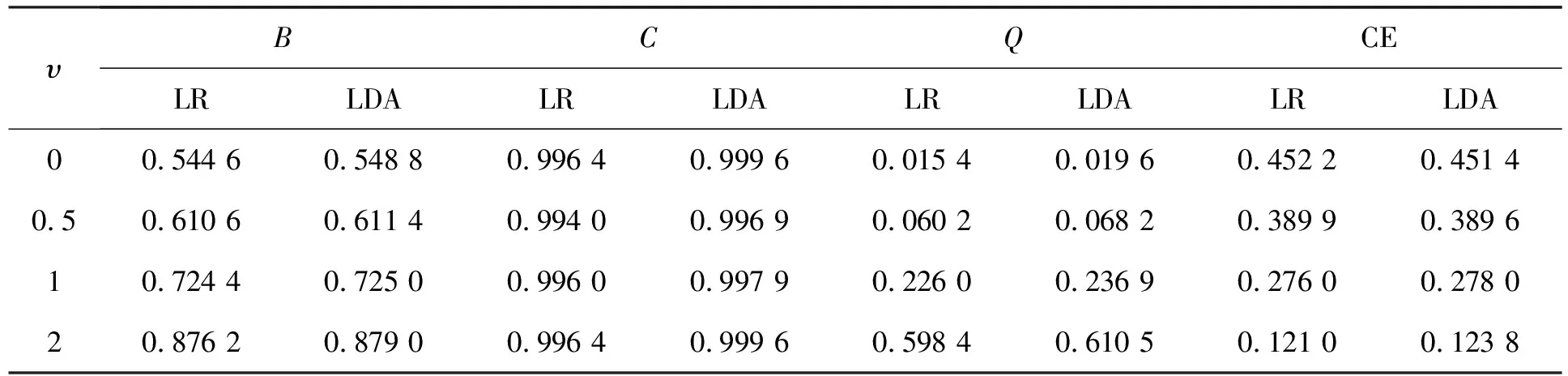
表1 类内均值间距离大小(υ)的影响

表2 解释变量(p)个数的影响

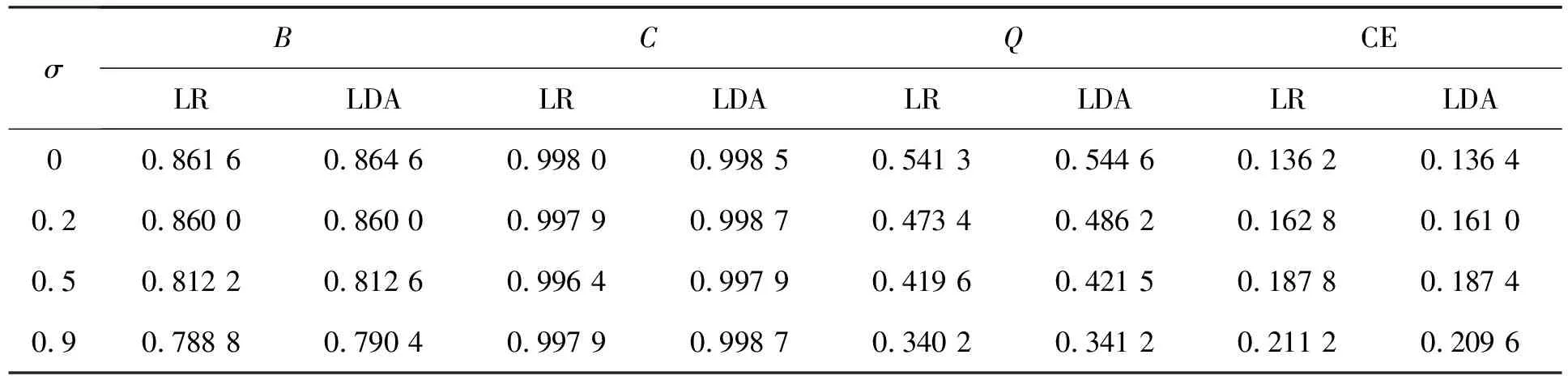
表3 解释变量间相关性(σ)的影响

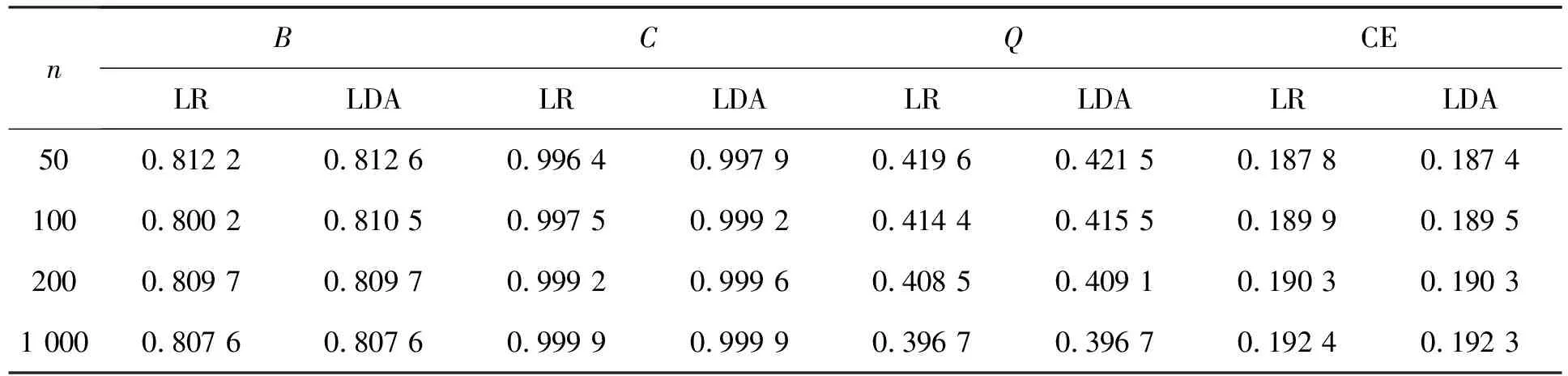
表4 类样本容量(n)的影响

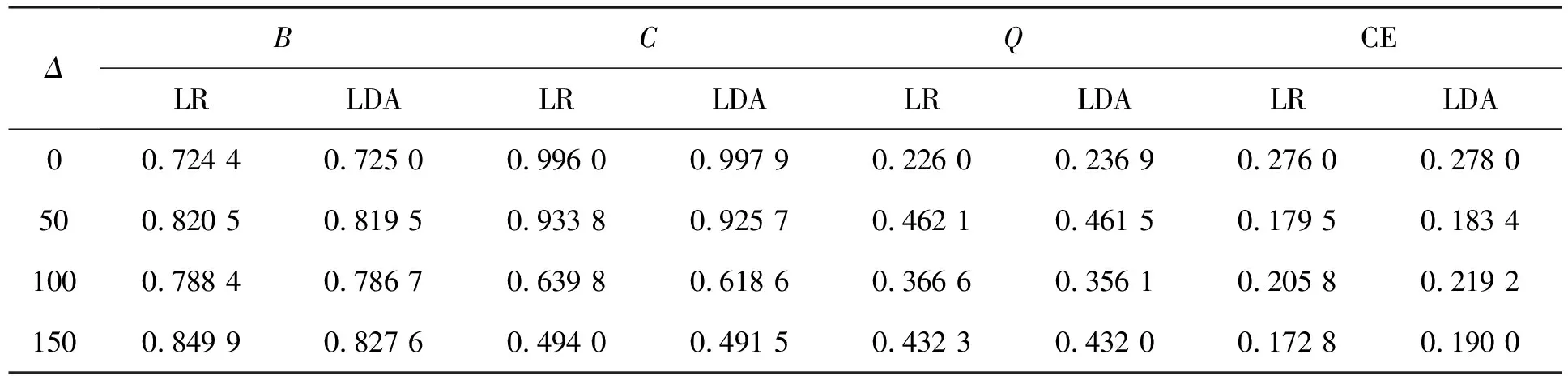
表5 类样本容量间差距(Δ)的影响

表6 非正态的影响

根据表1～表6,当数据符合正态假设时,类内均值间距离对两种方法都有影响,当距离较小时，两种方法都近乎失效,当距离增大后,线性判别分析的四种指标显示其效果更好;解释变量个数的变化几乎对模型没有任何影响,优于数据满足正态性假设,线性判别分析优于Logistic回归;变量间相关性增大时,两种方法的效果都变差,线性判别分析的四个指标仍普遍优于Logistic回归;随着样本量增大,Logistic回归和线性判别分析表现越来越相近,在类样本容量达到 1 000时,Logistic回归的C指标优于线性判别分析;当两类样本容量不同时,Logistic回归的预测精度明显优于线性判别分析。而当数据不再满足正态性假设时,明显Logistic回归的四个指标优于线性判别分析,此时Logistic回归效果更好。

4 结 语

针对二分类响应变量下的线性判别分析和Logistic回归进行了比较,目的在于给出不同情况下如何对两种方法进行选择。

为了方便比较三种方法,选定了四种指标值,分别是回判错误率CE和指标B、C、Q。模拟结果显示,大部分情况下,回判错误率不够灵敏,指标C的值变换幅度也不大,所以更关注指标B和Q的值。

首先在符合线性判别分析假设下,对两种方法进行比较,这时线性判别分析的效果普遍较好。但是随着样本量的增大,判别分析和Logistic回归的效果越来越相近,而当样本总量足够大时,Logistic回归的效果较好。另外,当两个类别的样本量不相等时,它们之间的差距越大,Logistic回归的效果越好。在不符合线性判别分析假设的情况下,Logistic回归大部分优于线性判别分析。

综上,当数据不符合正态性假设时,一般选择Logistic回归。当数据符合正态性假设时,如果样本量很大,或者两类样本量差距较大,此时Logistic为更优选择,其余情况下,线性判别分析效果更好。