Survey on cloud model based similarity measure of uncertain concepts

Shuai Li, Guoyin Wang ✉, Jie Yang

Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications,No. 2 Chongwen Street, Nan‘an District, Chongqin g, People’s Republic of China

Abstract:It is a basic task to measure the similarity between two uncertain concepts in many real-life artificial intelligence applications,such as image retrieval,collaborative filtering,public opinion guidance,and so on.As an important cognitive computing model, cloud model has been used in many fields of artificial intelligence. It can realise the bidirectional cognitive transformation between qualitative concept and quantitative data based on the theory of probability and fuzzy set. The similarity measure of two uncertain concepts is a fundamental issue in cloud model theory. Popular similarity measure methods of cloud model are surveyed in this study. Their limitations are analysed in detail.Some related future research topics are proposed.

1 Introduction

With the huge growth of available data, many artificial intelligence algorithms have surpassed human beings in some domains(e.g. image processing, natural language processing). However,the mechanism of processing information of human brain needs to be further studied. Cognitive science, which aims to reveal this mechanism, is the key issue of artificial intelligence. As the basic ability of cognition, to measure the similarity of concepts has become an important component in many applications. For example, it plays a crucial role in semantic information retrieval systems [1–3], sense disambiguation [1, 4], and information extraction [3, 5]. The present similarity measure of concepts can be roughly classified into two classes: (i) the methods based on structure use ontology hierarchy structure to compute the semantic similarity between concepts [2, 6–8], (ii) the methods based on information content use the information derived from concepts to measure the similarity. It is well known that uncertainty is an important property of semantic concept. Therefore, processing uncertain information of concepts is the inherent ability of human cognition. Researchers have devised many cognitive models to process uncertain concepts: probability models for randomness[9], fuzzy set models for vagueness [10], and rough set models for inconformity and incompleteness [11], but the reality is often more complex. On the one hand, a cognitive process often includes different forms of uncertainty simultaneously. On the other hand,different people have various cognitive results for an identical concept. Uncertainty is a challenge for artificial intelligence,because it is difficult to be defined precisely. However, it does not affect people’s communication [12–16]. Human cognition is more sensitive to qualitative concept than quantitative data. For example, people have no exact concept about 40°C water, but they can feel whether the water is hot or not. It means that data make no sense without special semantic. In human cognitive process,people can receive, store, and deal with plentiful uncertain information for identification, reasoning, decision making, as well as abstracting. Hence, it requires to study the uncertainty of human cognition in order to make that the artificial intelligence algorithms equip understanding and judgment like human, especially, the formal representation of knowledge [17–20].

Although some performances of artificial intelligence methods are excellent,the mechanism of these methods remains unclear entirely,which is considered as a challenge in the interpretability of some artificial intelligence methods. For implementing human cognitive process, cloud model (CM) [18] proposed by Li and Du describes the uncertainty of concept in human language, and reflects the unity of subjective cognition and objective world in human cognitive mechanism. There is a big gap between human cognitive mechanism and computer processing information mechanism.Computer merely processes information from samples, but human cognitive mechanism employs bidirectional cognition between knowledge and data. Human can abstract the uncertain knowledge from complex information under various backgrounds; also can generate new instances according to this knowledge. By utilising forward cloud transformation (FCT) and backward cloud transformation (BCT), CM realises transformation between qualitative knowledge and quantitative data, and implements bidirectional cognition between extension and intension of a concept, which simulates human cognitive process. CM reflects the uncertainty of qualitative concept itself. Meanwhile, it reveals the objective relationship between probability and fuzzy in uncertain concept. Furthermore, CM can be used to represent different cognitive results among various people for an identical concept. These differences are resulted by uncertainty of cognitive process and various experience of different people. Generally speaking, different people will have similar cognitive results which are not identical for the same concept. In [21], CM is naturally used to simulate the uncertain concept drift after diffusing among various people.

Since the above advantages of CM,it is an active study in various fields of artificial intelligence. For instance, in image process, after frequency of grey-scale values of pixels are transformed by BCT,image will be segmented into many parts induced by distance of CM [22–25]. In collaborative filtering, the system will calculate a score from the several nearest users according to similarity measure of CM [26–28]. In system performance evaluation, after local results conveniently transform to CM, aggregation of several close CM will form a global assessment [29–33]. Since similarity measure of CM plays a critical role in many fields, it has become a key issue for present research. Currently, many researchers devise various similarity measures for special problems, and have excellent performances [21, 26, 34–40]. Unfortunately, there is no uniform framework of similarity measure of CM, hence its criterions are absent in practice. Generally speaking, a suitable similarity measure of CM requires to distinguish the difference between two concepts and assures correct similarity conclusion under the background.Besides,it should be stable and high efficient,and have good interpretability in many situations.Current similarity measures defined by subjective methods dissatisfy the criterions above more or less. This paper surveys the popular similarity measures of CM and systematically analyses their distinctions and limitations. Therefore, to resolve current deficiencies, the relative solutions and future work directions are suggested.

The remainder is organised as follows.The relative definitions of CM and algorithms of FCT/BCT are introduced in Section 2.There are elaborate surveys and systematical analyses about similarity measure of CM in Section 3. Section 4 points out problems of current similarity measures of CM. Future perspectives and relative research topics are discussed in Section 5. Finally, we have some conclusions in Section 6.

2 Basic concepts of CM

In this section, we introduce the relative definitions of CM and algorithms of FCT/BCT.

Since the universality of Gaussian distribution and its wide applications, Gaussian CM (GCM) is a crucial model in diverse CMs, and its relative properties are merely discussed in this paper. GCM introduces three numerical characteristics including Ex, En, He which denote mathematical expectation, entropy, and hyper-entropy, and just accords with human thought [18–20, 32,33, 41, 42]. It depicts a unified framework of randomness and vagueness in human cognitive process, wherein the expectation represents the basic determinate domain of qualitative concept, the entropy represents the uncertainty for qualitative concept, and the hyper-entropy represents uncertainty for entropy.

Definition 1: [18]: Let U be a non-empty infinite set, and C (E x,En,He). If there is a number x ∈U, which is a random realisation of the concept C and satisfies x ～RNEx,y, where y ～RN(En,He) and the certainty degree of x on U is μ( x)=exp, then the distribution of x on U is a Gaussian cloud or normal cloud, and each x is defined as a Gaussian cloud drop.

Drops from various regions make different contributions to the CM. Due to distribution property of Gaussian distribution, 99.7%of cloud drops fall into interval [Ex-3En, Ex+3En]. It means that we can neglect the drops out of this interval which is called core region of CM. This is the ‘3σ’ principle of the Gaussian cloud.In the same way, 99.7% certainty degree value μ(x ) range from curve y1=which is called the inner envelope, towhich is called the outer envelope. We also call curve y=exp-(x-Ex)2/2En2expectation curve. Fig. 1 shows the shape and the characteristic curves of C (20,6,1). If 0 ＜He ＜drops aggregate to an explicit CM, otherwise, CM is atomised, and drops are scattered. Fig. 2 shows atomisation of C (20,6,4). GCM is closely related to Gaussian distribution [43]. Two Gaussian kernel,inner envelope and outer envelope,form boundaries of GCM, GCM degrade into Gaussian kernel when He=0. In other words,Gaussian kernel is an extreme situation of GCM.

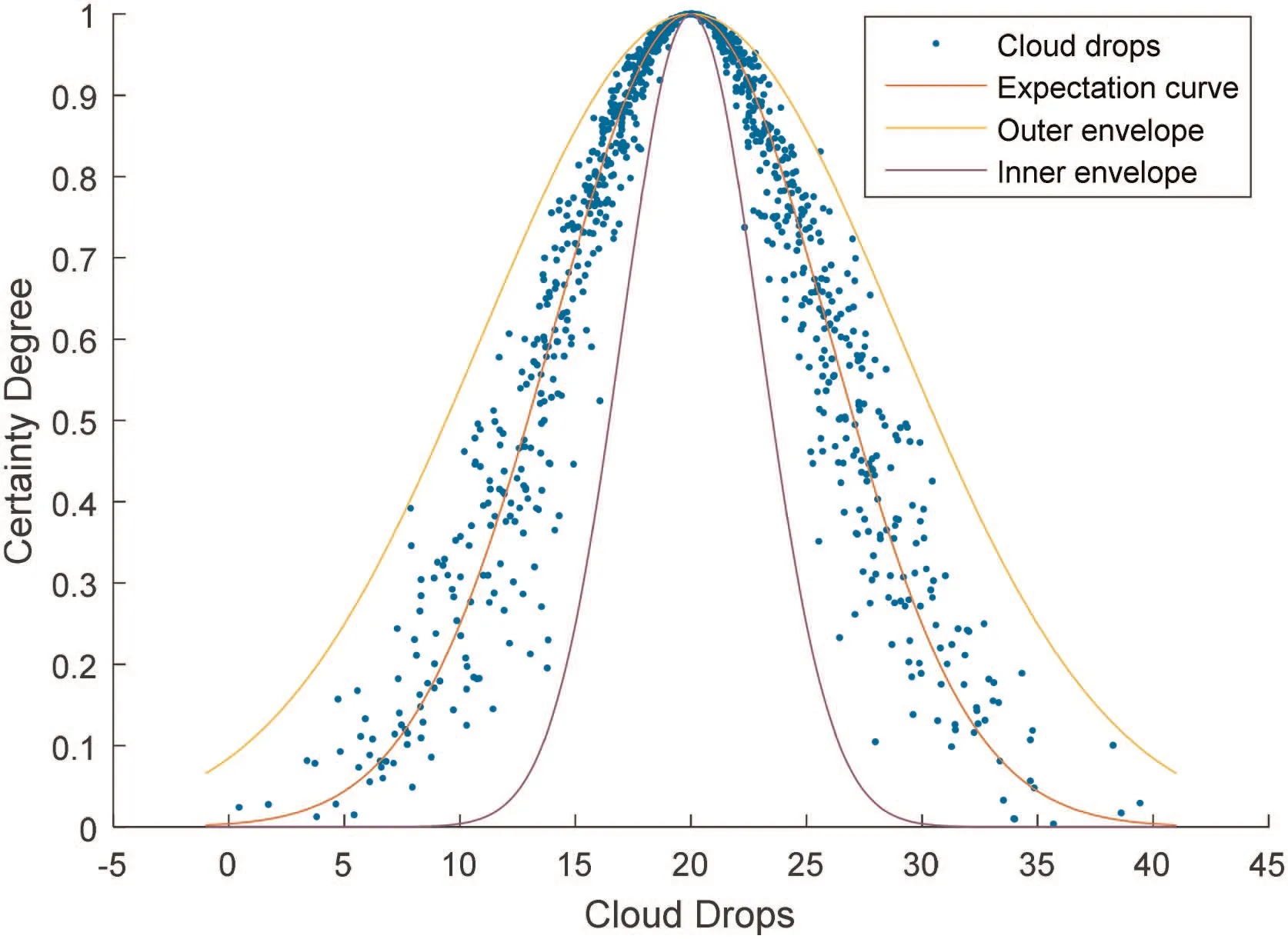
Fig. 1 Characteristic curves of C (20,6,1)

Transformation from conceptual extension to intension is more complex than FCT (Algorithm 1 in Fig. 3). There are many algorithms,which are called BCT algorithms[18,43],to realise this transformation in different situations, such as BCT-1stM, BCT-4thM,MBCT-SR. BCT requires calculability and low complexity, and minimises the computational error. The popular BCT is introduced as follows (Algorithm 2 in Fig. 4).

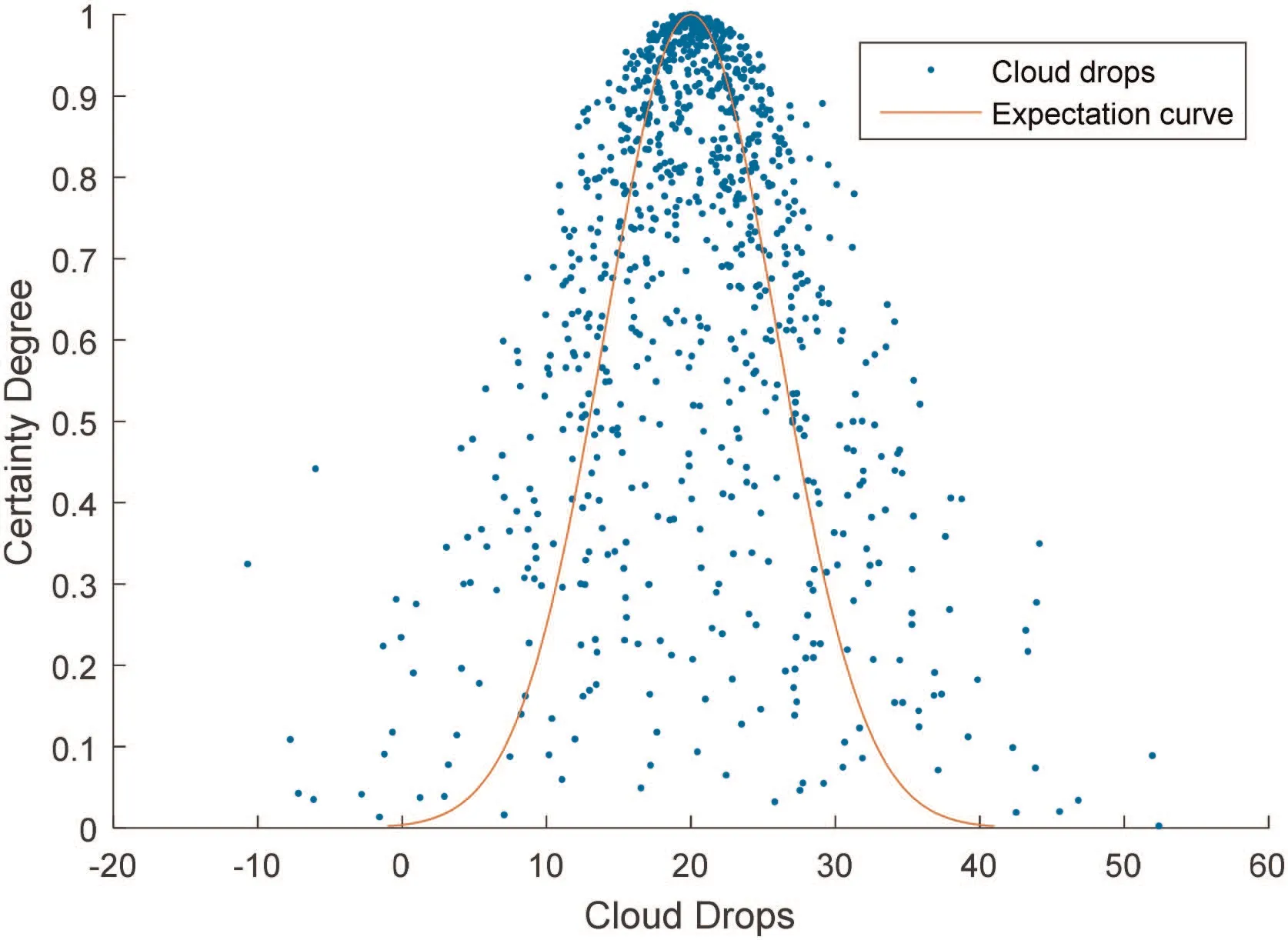
Fig. 2 Atomisation of C (20,6,4)

Fig. 3 Algorithm 1 [18]: FCT algorithm

Fig. 4 Algorithm 2 [18]: BCT based on the first-order absolute central moment (BCT-1stM)

3 Similarity measure of CM

It is a great challenge to deal with uncertain problems in big data era. Although information transmission and storage technology have developed to promote the ability of big data processing,it is impossible to acquire the complete and consistent knowledge from huge amount data generated every second. Besides, since human cognition is an uncertain process, it is a problem to design reasonable and objective method to quantify uncertainty in various tasks. Different people have similar (but not the same) cognitive results for an identical concept, owing to uncertainty of bidirectional cognition between extension and intension. In the multi-granularity cognitive computing, it is a key issue to merge similar knowledge from low granularity level into a high granularity knowledge. This process is called inter-transformation of granularity layers in multi-granularity space. Hence, a reasonable similarity measure of concepts should be required in many artificial intelligence fields. Since CM simultaneously describes vagueness and randomness, and conveniently transforms between extension and intension in human cognition. Researchers have proposed many similarity measures of CM under various backgrounds.

Currently, similarity measure of CM is primarily described in three aspects: conceptual extension, numerical characteristics, and characteristic curves, respectively. In extension aspect, Zhang et al.[44] first proposes calculating average distance of the extension to judge whether two CMs are similar. Many researchers define similarity based on numerical characteristics of CM. Likeness comparing method based on CM (LICM) [26] employs included angle cosine of vectors which are composed by numerical characteristics to calculate the similarity. Compared with numerical characteristics, characteristic curves include richer connotation than numerical characteristics. Thus, many researchers study the similarity of CM by characteristic curves. Li et al. [36] proposes expectation based on CM (ECM) and max boundary based on CM(MCM), which define similarity measure by overlapping area of characteristic curves. Inspired by the relationship between Gaussian distribution and GCM, researchers utilise distance of probability distributions, i.e. Kullback–Leibler divergence (KLD)[23], earth movers distance (EMD) [40], square root of the Jensen-Shannon divergence [45], to describe the concept drift which is reflected by distance between two CMs. In this section,we introduce primary similarity measures of CM, and analyse their merits and demerits.

3.1 Similarity measure based on concept extension

CM is composed by abundant drops and their certainty degree. Although a single drop is insignificant in CM, abundant drops can express a concept due to stable some statistical characteristics. Distribution of drops is non-uniform. They focus on the top of cloud, while are sparse on the bottom. These statistical characteristics are used to define the similarity measure of CM.

Calculating distance of cloud drops is intuitionistic to understand and implement. It is crucial step to calculate the Distance （j ）from step 2 to step 3 in Algorithm 3 (Fig. 5). The algorithm prefers judging whether two CMs are similar rather than similarity value itself, because that Distance （j）is affected by the sample size n and other random factors. Meanwhile, the threshold δ is subjective value. Various thresholds will lead to different results of similarity measure. Furthermore,is a very huge number even if n1and n2are small. For instance,=497503 for=996 and n =998, complexity of the algorithm is very high. Cai et al. [39] introduces fuzzy cut to reduce the drop scale, and then decreases the complexity of algorithm. But it still cannot overcome the defect of instability. In addition, similarity measure based on cloud drops distance is not equal to 1 of two identical concepts, because drops are generated with random. It violates human cognition. To address these defects, it is necessary to study stable similarity measure of CM which conforms to human cognition.

Fig.5 Algorithm 3:concept extension based similarity measure(CS)[44]

3.2 Similarity measure based on numerical characteristics

Uncertain information is involved in conceptual intension and is expressed by numerical characteristics of CM. In collaborative filtering, LICM denotes CM by a 3D-vector which is composed by numerical characteristics. Similarity measure is defined by included angle cosine of these vectors.

Definition 2: [26]: Let v1and v2be two 3D-vectors composed by numerical characteristics with respect to two CMsThe similarity measure of them is defined by included angle cosine, i.e.

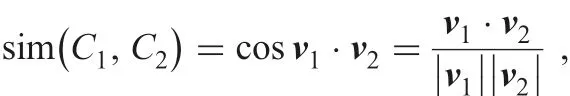
The value of similarity ranges from 0 to 1. When two CMs are identical, the similarity value equals to 1. It is more stable and has higher efficiency than Algorithm 3. However, it does not reflect the relationships among numerical characteristics. It will violate human cognition in some situations. For example,it is obvious that two CMs are not identical.

3.3 Similarity measure based on characteristic curves

Conceptual intension also can be denoted by characteristic curves which illustrate the variation range of the certainty degree of cloud drops. The area under the characteristic curve indicates the uncertain information of a concept. It is obvious that larger overlapping area under characteristic curves of two CMs indicates higher similarity between them. Similarity measure based on characteristic curves, ECM and MCM, are initiatively introduced in [36], and are systematically analysed from properties and algorithm complexity. Since they include inter-connections among numerical characteristics, they obtain higher classifying precision than LICM. It is verified in [36] by classification of time series.

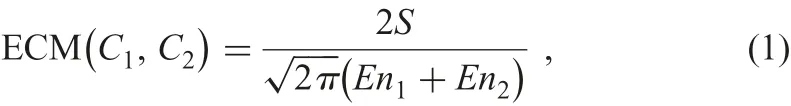
where S (blue area in Fig. 6) is overlapping area under expectation curves. The value of this similarity measure also ranges from 0 to 1, sinceandequal to the area of region under expectation curve of C1and C2, respectively. It equals to 1 with two identical CMs and equals to 0 if no intersection in core region of C1and C2. Following algorithm is ECM, and MCM can be calculated analogously by replacing expectation curves with outer envelopes.

Fig. 6 Overlapping area under expectation curves of C1 (2 2,5,0.5) and C2 (1 5,4,0.45)

Fig. 7 Algorithm 4 [36]: ECM

Algorithm 4(Fig.7)is efficient,stable,and explicable. It depicts similarity on geometrical perspective that reflects the relationship between mathematical expectation and entropy, but it neglects hyper-entropy. Although hyper-entropy is considered in MCM, it will fail when hyper-entropy is very large. Based on this work,researchers propose improved methods to Algorithm 4. Restricted hyper-entropy expectation method-based CM (RHECM) [46]utilises an area ratio of ‘soft conjunction’ to ‘soft disjunction’. The ratio is determined by combination of entropy and hyper-entropy.Similarity is defined by overlapping area under characteristic curves, whether ECM, MCM or RHECM tend to 0 when a concept is clear due to their small area under characteristic curves.For two concepts C1(15,0.01,0.001) and C2(15,5,1), it is obvious that C1is more accurate than C2. It violates human cognition that their similarity is approximately 0 by ECM. To solve this problem, concept skipping indirect approach of CM[47], which is inspired by concept skipping in multi-granularity space, uses area ratio of basic concepts to a synthetical concept to define the similarity indirectly. Mutual membership degree based similarity measurement between CMs [48] calculate proportion of mutual overlapping area under expectation curve and average the proportion to determine similarity.

Wang et al. [43] indicate that there is close relationship between Gaussian distribution and GCM. Many researchers use distance of probability distributions to define the dissimilarity. Concept drift means the distance of two concepts in knowledge space, and smaller distance indicates higher similarity of them. Xu and Wang[21] initially employ KLD of outer envelope of CM to calculate the drift. With EMD applied to describe distance of multi-granular knowledge space [49, 50] successfully, Yang et. al. [40] propose

the multi-granularity similarity measure. These methods are stable,

efficient, explicable but have low discriminability. For example,=1 where C1(5,9,1) and C2(5,6,2) in [51], it is obvious they are not identical.

Table 1 shows the comparisons among similarity measures mentioned above on discriminability, efficiency, stability, and interpretability perspectives. Discriminability means that the similarity measure can distinguish the difference between two concepts if they are not identical.Efficiency means the time complexity of computing similarity between two concepts. Stability means that the value of similarity is invariant in multiple computation. Interpretability means that the computing process of similarity measure is interpretable. As analysed above, CS can distinguish any two concepts if they are not identical, but it has high time complexity. Although it is very intuitionistic to compute similarity by conceptual extension,the results are different every time for two invariant concepts.LICM has high efficiency and stability, but it does not distinguish the difference between two concepts which have the same proportion of numerical characteristics.Besides,considering numerical characteristics as a vector does not reflect the relationships among the numerical characteristics, which lacks interpretability of computing process.MCM, ECM, KLCM, EMDCM are all similarity measures based on characteristic curves. They have high efficiency and stability like LICM,but they do not find the difference between two different concepts in some special situations due to neglecting the variation of hyper-entropy. Moreover, they only have partial interpretability due to the absence of relationship between entropy and hyper-entropy.

Fig.8 shows properties on similarity measures of the three categories.There are four colours to represent different properties.If a kind of similarity measure lacks some properties, then these properties are denoted as light colour and are separated from entirety. In summary,similarity measures based on extension have the highest discriminability and interpretability,but they are unattainable in practice due to their lowest efficiency and instability. Although methods based onnumerical characteristics have high efficiency and stability,considering numerical characteristics as a vector results in restricting these methods in some situations. Characteristic curves based methods try to compute the similarity in intension aspect,and have high efficiency,stability,and medium interpretability.However,it has low discriminability in some extreme cases.

Table 1 List of similarity measures of CM

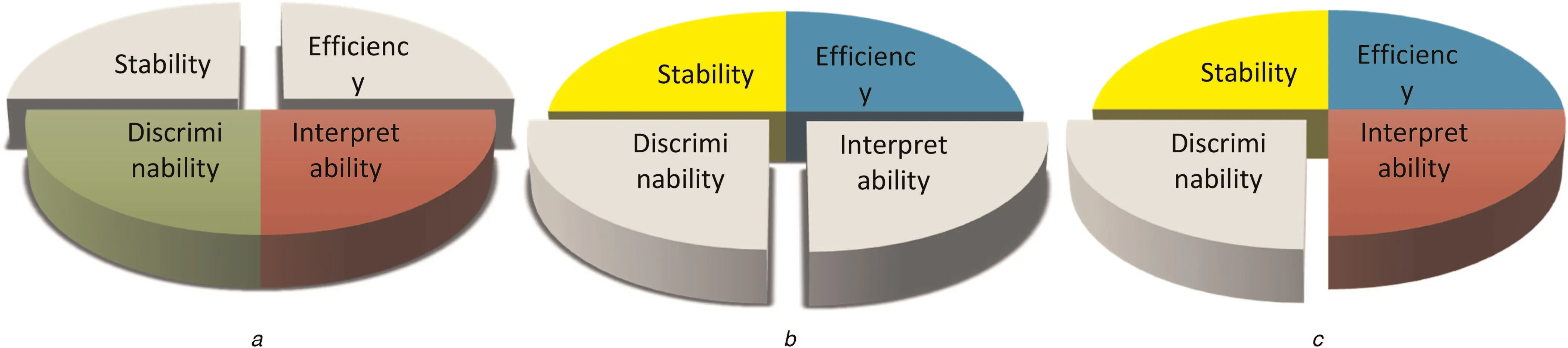
Fig. 8 Properties of similarity measures based on three aspects

4 Problems of current similarity measures

4.1 Absence of domain-specific

Similarity measure of CM is studied based on extension (cloud drops, uncertainty degree) and intension (numerical characteristics,characteristic curves), but domain-specific is barely noticed, which leads to incorrect results in certain situations sometimes. Extension reflects similarity of CM directly, but it is incapable for applications due to the complexity of algorithm from analyses above. Although three numerical characteristics indicate stable tendency of cloud drops, their meanings are different. Hence, they should be computed by a reasonable method in various situations.In fact, similarity measure is used to evaluate similarity extent of CM, it deserves to study that the same value of similarity measure expresses different similarity extent under various backgrounds. In other words, different concepts have different sensitivity to the value of similarity measure.

Example 1:In the task of time series anomaly detection,similarity is major impacted by distribution of data and variation of tendency.Two-dimensional normal cloud representation has been proposed to dimensionality reduction for time series [52–54]. On the raw date-time, expectation Ex equals to mean of raw date, which is related to the statistics of time series in the time window t.Entropy En and hyper-entropy He reflect the range of variation,which are small changes in different time windows. The changing of tendency over time is focused on the residual time. Expectation Ex reflects macro-tendency of variation, and entropy En,hyper-entropy He describe uncertainty of the tendency. Tendency changes little in different time windows, so similarity on residual time should be more sensitive to value of similarity measure than it on raw time. For example, for2,4.8,1.2) and C2(10,6,2) on raw time, although there is a gap between expectations, the difference of variation is little. They are regarded as distribution of same time series in different time windows.However, they are considered as an anomalous time series on residual time owing to the gap of expectations, even though the same value of similarity measure is regarded as normal on raw time.

4.2 Absence of unified evaluation criterion

Current similarity measures lack reliable theoretical basis from analyses of previous section. It absents stability based on extension and interpretability base on intension. Various meanings of three numerical characteristics are a universal objective fact. As the most representative and typical sample of the qualitative concept, mathematical expectation Ex is most significant for similarity measure of CM. However, when similarity measure is only related with data distribution rather than other attributes, the value of expectation is unimportant. For example, in image processing, similarity measure is only related with its distributions,but irrelated with its position. Similarity is not simple combination among numerical characteristics but should equip with the clear physical meaning or reliable theoretical supporting.

Example 2:In shooting training,athletes A,B,C are evaluated by ten shooting results. Scores of them are transformed to CM C1(7.9,0.1,0.03), C2(8.0,1.0,0.08), C2(7.5,0.1,0.01) by BCT.A has stable performance fluctuating around 7.9, and scores are more concentrated.Mean scores of B fluctuates around 8.0 is higher than A, but his performance is instable due to sharp variance.While, C shows the most stable, but has lowest mean scores. Now we try to evaluate their similarity of shooting abilities. There are three different results: from shooting accuracy, similarity(A,B)＞similarity(B,C)＞similarity(A,C); on psychological quality perspective, similarity( A,C)＞similarity( A,B)＞similarity(B,C); in comprehensive assessment, similarity(A,C)＞similarity(B,C)＞similarity(A,B). However, a unified evaluation criterion is absent in similarity.Hence,three numerical characteristics should be given different weights to measure similarity in various situations.

4.3 Absence of suitable similarity measure for extensive situations

From analyses above,we know that a suitable similarity measure of CM should be equipped with stability, efficiency, discriminability and interpretability. Section 3 shows that current methods dissatisfy some criterions above. It is hard to establish a suitable similarity measure on theory perspective. This will cause inconformity in some applications.

Example 3: For CMs C1(10,5,1), C2(5 ,2.5,0.5), C3(1 0,5,0.4),and C4(10,2,2), Table 2 shows their similarity values of LICM,ECM, and MCM. Fig. 9 shows the shapes of C1, C2, C3, and C4.They are four CMs to represent different concepts by Definition 1.Based on LICM, similarity of C1and C2is equal to 1. They have same proportion of numerical characteristics. Due to significant differences between expectations of them, similarities of C1and C2are equal to 0.48 and 0.57 calculated by ECM and MCM,respectively. ECM-based similarity of C1and C3equals to 1 because they have same expectation curves. C1and C3are indistinguishable by ECM. MCM-based similarity of C1and C4equals to 1 because they have same outer envelopes, but there are tremendous differences between them. From Fig. 9, it is easy to find that C1is an explicit concept, but C4is a chaotic concept.

Table 2 Similarity values of LICM,ECM and MCM

Fig. 9 Shapes of different CMs in Example 3

Table 2 illustrates that the discriminability of ECM and MCM surpass LICM. However, ECM and MCM are useless to distinguish concepts in extreme situations, e.g. C1, C3and C1, C4.In a word, since these similarity measures have low discriminability, similarity values of two CMs are various by different methods. These similarity measures will cause inconformity results in applications. In other words, there is an absent suitable similarity measure to extensive situations.

5 Future perspectives

Based on semantic relationship, similarity measure of concepts is a key issue on knowledge acquisition. It is important to reveal the complex relationship of aggregated multi-granularity concepts from data in high-dimensional space. Similarity measure of CM deserves research, because the semantic interpretation of uncertainty of knowledge is described by CM on probability and fuzziness perspectives. By analysing problems of current similarity measures in Section 4, due to complex uncertainty of concepts,current methods reflect similarity on partial uncertain information.For example, characteristic curves based similarity measures only consider uncertainty of concepts, i.e. the relationship between expectation Ex and entropy En, but neglect the other uncertainty,i.e. the relationships between entropy and hyper-entropy.Hyper-entropy is often fixed as special value in these methods. In Example 3, because hyper-entropy of C1and C3are fixed as 0,they are indistinguishable in ECM. From Section 4, there are two aspects of research in the future. (i) We study similarity measures in specific situations. These situations only consider partial uncertain information, e.g. to aggregate the similar parts of image,we only consider uncertainty of entropy En and hyper-entropy He in image segmentation. It tolerates more generalised similar pixels clustering. So, similarity measures of high discriminability are unnecessary in this task. (ii) In some classifying or clustering task,we require high discriminability to distinguish two concepts.Similarity measures of CM mentioned above are no longer inapplicable. A method with high discriminability should be study in the future.

In current works, similarity measures in specific situations are widely studied in various domains. We only discuss the second problem. It is obvious that neglecting the uncertain information causes low discriminability in similarity measures. Next, we try to propose the formalised definition of similarity measure of CM,then discuss the uncertainty based similarity of CM.

5.1 Similarity measure of CM based on axiomatisation

Although there are plenty of similarity measures of CM, a unified framework is required to interpret the similarity on theory perspective. Based on the distinction of elements, researchers have defined distance between two sets. Distance of fuzzy sets can be defined by this way, merely replacing membership relation by membership function [55–57]. Although random and fuzzy are entirely different in essence, uncertainty measures and distances have unified forms. For example, information entropy originated from coding theory is used to measure uncertainty of fuzzy sets.KLD originated from the similarity measure between two random variables, which is also used to measure the distance between two fuzzy sets. Axiomatisation of similarity of fuzzy sets is given as follows.

Definition 3:Let X be the universal set,and F (X )be the class of all fuzzy sets of X. s:F (X )×F (X )→R+is a similarity measure on F (X ) if it satisfies the axioms as follows:

(S1) s(A,B)=s(B,A), ∀A,B ∈F (X ) (Symmetric),

(S2) s(A,B)=1 iff A=B (Reflexivity),

(S3) If A ⊂B ⊂C, then s(A,B)≥s(A,C) and s(B,C)≥s(A,C),∀A,B,C ∈F (X ) (Transitivity).

Related to the similarity, distance of CM is a measure that indicates dissimilarity between CM. It is obvious that the similarity and distance are two dual measures. Formalised definition of distance of fuzzy sets is defined as follows:

Definition 4:Let X be the universal set,and F (X )be the class of all fuzzy sets of X.d:F (X )×F (X )→R+is a similarity measure on F (X ) if it satisfies the axioms as follows:

(D1) d (A,B)=d (B,A), ∀A,B ∈F (X ) (Symmetric),

(D2) d (A,B)=0 iff A=B (Reflexivity),

(D3) If A ⊂B ⊂C, then d (A,B)≤d (A,C) and d (B,C)≤d (A,C),∀A,B,C ∈F (X ) (Transitivity).

Inspired by similarity measure and distance of fuzzy sets, it deserves to research the similarity measure of CM satisfying the axiomatisation based on the distinction of common elements in future.

5.2 Similarity measure of CM based on uncertainty

From analyses in Section 4,we require a rational criterion to measure similarity. As an important feature of concept, uncertainty reflects essential difference between human cognition and computer processing. A suitable similarity measure of CM should reflect the similarity based on uncertainty. Unlike probability and fuzzy set, it is intractable that CM includes more complex uncertainty. To deal with complex uncertain problems, many extended fuzzy models,which approximate to the crisp degree of membership by an interval, such as interval-value fuzzy sets [58], intuitionistic fuzzy sets [59] and vague sets [60], have been proposed. Both type-2 fuzzy sets [61] and CM employ more complex uncertain degree membership to characterise qualitative concepts. There are many different between type-2 fuzzy sets and CM [62–64]. Type-2 fuzzy sets study the fuzziness of membership value, which is considered as second-order fuzziness, and CM studies the uncertainty of membership value, which is considered as fuzziness, randomness,and the connection of them. The membership degree of type-2 fuzzy sets can be represented by a certain function or clear boundary on interval [0,1]. But based on probability measure space, membership of CM is generated by random process (FCT).Hence, its membership degree has neither certainty nor boundary,but has a stabilisation tendency. Furthermore, type-2 fuzzy sets always have consecutive uncertain region (Fig. 10a), nevertheless the uncertain region of CM composed of discrete points which is generated by a random process (Fig. 10b). In other words, the different uncertain regions are formed by FCT for an identical cloud concept every time. Although many differences of them are mentioned above, this approach to quantify similarity can be introduced in CM. As they involve two-order uncertainties. It will improve present quantified methods of uncertainty, which only consider relationship between expectation and entropy. Inspired by this, it is valuable to research similarity measure of CM based on two-order uncertainties.

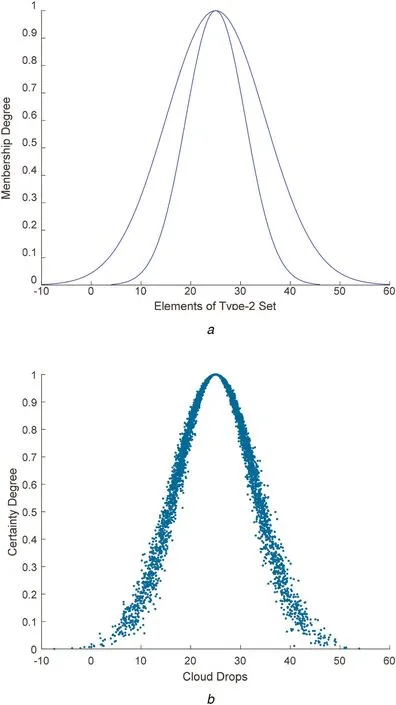
Fig. 10 Interval type-2 fuzzy sets and CM

6 Conclusion

The theory of CM is a useful tool to describe uncertain problems and has been gradually matured. CM also plays a significant role in uncertain artificial intelligence due to its strong ability for describing fuzziness, randomness and their connection. It realises the bidirectional cognition between data and knowledge by using FCT and BCT. As an important method, similarity measure of CM has been widely applied in many domains. In this paper, we have divided present similarity measures of CM into three categories: conceptual extension based similarity,numerical characteristics based similarity, and characteristic curves based similarity. Moreover, we have analysed their merits and deficiencies in four aspects, i.e. discriminability, efficiency,stability, and interpretability. Then, we discuss some problems of current similarity measures in applications. Finally, we propose some future perspectives which can help us to address the problems of similarity measures in theory and application. This work will provide some valuable references for researchers in the future and will promote the studies on CM in artificial intelligence.

7 Acknowledgments

This work is supported by the National Natural Science Foundation of China (no. 61572091, no. 61772096).

8 References

[1] Budanitsky, A., Hirst, G.: ‘Evaluating WordNet-based measures of lexical semantic relatedness’, Comput. Linguist., 2006, 32, (1), pp. 13–47

[2] Nguyen,H.A.,Al-Mubaid,H.:‘New ontology-based semantic similarity measure for the biomedical domain’. IEEE Int. Conf. on Granular Computing, Atlanta,Georgia, USA, May 2006, pp. 623–628

[3] Sim,K.M.,Wong,P.T.:‘Toward agency and ontology for web-based information retrieval’, IEEE Trans. Syst. Man Cybern. C, Appl. Rev., 2004, 34, (3),pp. 257–269

[4] Rus, V., Niraula, N., Banjade, R.: ‘Similarity measures based on latent dirichlet allocation’. Computational Linguistics and Intelligent Text Processing,Samos, Greece, March 2013, pp. 459–470

[5] Laza, R., Pavón, R., Reboirojato, M., et al.: ‘Assessing the suitability of MeSH ontology for classifying medline documents’. Int. Conf. on Practical Applications of Computational Biology & Bioinformatics, Salamanca, Spain,April 2011, pp. 337–344

[6] Fellbaum, C., Miller, G.: ‘Combining local context and wordnet similarity for word sense identification’, WordNet: An Electron. Lexical Database, 1998, 49,(2), pp. 265–283

[7] Rada,R.,Mili,H.,Bicknell,E.,et al.:‘Development and application of a metric on semantic nets’, IEEE Trans.Syst. Man Cybern., 1989, 19, (1), pp. 17–30

[8] Wu, Z., Palmer, M.: ‘Verbs semantics and lexical selection’. Proc. of the 32nd annual meeting on Association for Computational Linguistics Las Cruces, New Mexico, USA, June 1994, pp. 133–138

[9] Li, D.Y., Liu, C.Y., Du, Y., et al.: ‘Artificial intelligence with uncertainty’,J. Softw., 2004, 15, (11), pp. 1583–1594

[10] Zadeh, L.A.: ‘Fuzzy sets’, Inf. Control, 1965, 8, (3), pp. 338–353

[11] Pawlak, Z.: ‘Rough set’. Int. J. Comput. Inf. Sci., 1982, 11, (5), pp. 341–356

[12] Chen,G., Xu, Y.:‘Special issue on dealing with uncertainty in data mining and information extraction’, Inf. Sci., 2005, 173, (4), pp. 277–279

[13] Hsu, M., Bhatt, M., Adolphs, R., et al.: ‘Neural systems responding to degrees of uncertainty in human decision-making’, Science, 2005, 310, (5754),pp. 1680–1683

[14] Montero, J., Da, R.: ‘Modelling uncertainty’, Inf. Sci., 2010, 180, (6),pp. 799–802

[15] Sabahi, F., Akbarzadeh, T.M.R.: ‘A qualified description of extended fuzzy logic’, Inf. Sci., 2013, 244, pp. 60–74

[16] Yager, R.R.: ‘Modeling uncertainty using partial information’, Inf. Sci., 1999,121, (3–4), pp. 271–294

[17] Alexandridis, K., Maru, Y.: ‘Collapse and reorganization patterns of social knowledge representation in evolving semantic networks’, Inf. Sci., 2012, 200,pp. 1–21

[18] Li, D.Y., Du, Y.: ‘Artificial intelligence with uncertainty’ (Chapman & Hall/CRCPress, Boca Raton, 2008)

[19] Li,D.Y.,Liu,C.,Gan,W.Y.:‘A new cognitive model:cloud model’,Int.J.Intell.Syst., 2009, 24, (3), pp. 357–375

[20] Liu, C., Li, D.Y.: ‘Study on the universality of the normal cloud model’, Eng.Sci., 2004, 6, (8), pp. 28–34

[21] Xu, C.L., Wang, G.Y.: ‘Excursive measurement and analysis of normal cloud concept’, Comput. Sci., 2014, 41, pp. 9–14

[22] Li,W.S.,Wang,Y.,Du,J.,et al.:‘Synergistic integration of graph-cut and cloud model strategies for image segmentation’,Neurocomputing,2017,257,pp.37–46

[23] Xu, C.L., Wang, G.Y.: ‘A novel cognitive transformation algorithm based on Gaussian cloud model and its application in image segmentation’, Numer.Algorithms, 2017, 76, (4), pp. 1039–1070

[24] Li, W.S., Li, F.Y., Du, J.: ‘A level set image segmentation method based on a cloud model as the priori contour’, Signal. Image. Video. Process., 2019, 13,(1), pp. 103–110

[25] Vahid, B., Jahangiri, A., Machiani, S.G.: ‘Multi-class US traffic signs 3D recognition and localization via image-based point cloud model using color candidate extraction and texture-based recognition’, Adv. Eng. Inf., 2017, 32,pp. 263–274

[26] Zhang, G.W., Li, D.Y., Li, P., et al.: ‘A collaborative filtering recommendation algorithm based on cloud model’, J. Softw., 2007, 18, (10), pp. 2403–2411

[27] Xiao, Y.P., Sun, H.C., Dai, T.J., et al.: ‘A rating prediction method based on cloud model in social recommendation system’, Acta Electron. Sin., 2018, 46,(7), pp. 1762–1776

[28] Jin-Gang, S., Li-Rong, A.I.: ‘Collaborative filtering recommendation algorithm based on item attribute and cloud model filling’, J. Comput. Applic., 2012, 32,(3), pp. 658–660

[29] Zhang, H.Y., Ji, P., Wang, J.Q., et al.: ‘A neutrosophic normal cloud and its application in decision-making’, Cogn.Comput., 2016, 8, (4), pp. 649–669

[30] Gao, H.B., Zhang, X.Y., Zhang, T.L., et al.: ‘Research of intelligent vehicle variable granularity evaluation based on cloud model’, Acta Electron. Sin.,2016, 44, (2), pp. 365–373

[31] Wu,A.Y.,Ma,Z.G.,Zeng,G.P.:‘Set pair fuzzy decision method based on cloud model’, Chin. J. Electron., 2016, 25, (2), pp. 215–219

[32] Wang, J.Q., Peng, L., Zhang, H.Y., et al.: ‘Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information’, Inf. Sci., 2014, 274, pp. 177–191

[33] Wang,J.Q.,Peng,J.J.,Zhang,H.Y.,et al.:‘An uncertain linguistic multi-criteria group decision-making method based on a cloud model’, Group Decis. Negot.,2015, 24, (1), pp. 171–192

[34] Wu, L., Zuo, C., Zhang, H.: ‘A cloud model based fruit fly optimization algorithm’, Knowl.-Based Syst., 2015, 89, pp. 603–617

[35] Liu,H.C.,Xue,L.,Zhiwu,L.,et al.:‘Linguistic Petri nets based on cloud model theory for knowledge representation and reasoning’, IEEE Trans. Knowl. Data Eng., 2018, 30, (4), pp. 717–728

[36] Li,H.L., Guo,C.H.,Qiu,W.R.:‘Similarity measurement between normal cloud models’, Acta Electron. Sin., 2011, 39, (11), pp. 2561–2567

[37] Zhang, Y., Zhao, D.N., Li, D.Y.: ‘The similar cloud and the measurement method’, Inf. Control, 2004, 33, (2), pp. 129–132

[38] Zhang, J.J., Wang, H.B., Chen, J.L., et al.: ‘An improved algorithm for determining membership conception based on cloud model’, Comput. Technol.Dev., 2007, 17, (10), pp. 65–68

[39] Cai,C.B.,Fang,W.,Zhao,J.,et al.:‘Research of interval-based cloud similarity comparison algorithm’, J. Chin. Comput. Syst., 2011, 32, (12), pp. 2456–2460

[40] Yang, J., Wang, G.Y., Li, X.K.: ‘Multi-granularity similarity measure of cloud concept’. Int. Joint Conf. on Rough Sets, Santiago de Chile, Chile, October 2016, pp. 318–330

[41] Li, D.Y., Meng, H.J., Shi, X.M.: ‘Membership clouds and membership cloud generators’, J. Comput. Res. Dev., 1995, 6, pp. 15–20

[42] Yang, X., Yan, L., Zeng, L.: ‘How to handle uncertainties in AHP: the cloud delphi hierarchical analysis’, Inf. Sci., 2013, 222, pp. 384–404

[43] Wang, G.Y., Xu, C.L., Li, D.Y.: ‘Generic normal cloud model’, Inf. Sci., 2014,280, (280), pp. 1–15

[44] Zhang, Y., Zhao, D.N., Li, D.Y.: ‘The similar cloud and measurement method’,Inf. Control, 2004, 33, (2), pp. 129–132

[45] Yang, J., Wang, G.Y., Zhang, Q.H., et al.: ‘Similarity measure of multi-granularity cloud model’, Pattern Recognit. Artif. Intell., 2018, 31, (8),pp. 677–692

[46] Yan, Y., Tang, Z.M.: ‘Pertinence measurement of cloud model by using expectation-entropy curves’, Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2012, 40, (10), pp. 95–100

[47] Zha,X.,Ni,S.H.,Xie,C.,et al.:‘Indirect computation approach of cloud model similarity based on conception skipping’, Syst. Eng. Electron., 2015, 37, (7),pp. 1676–1682

[48] Fu, K., Xia, J.B., Wei, Z.K., et al.: ‘Similarity measurement between cloud models based on mutual membership degree’, Trans. Beijing Inst. Technol.,2018, 38, (4), pp. 405–411

[49] Yang, J., Wang, G.Y., Zhang, Q.H.: ‘Knowledge distance measure in multigranulation spaces of fuzzy equivalence relations’, Inf. Sci., 2018,448-449, pp. 18–35

[50] Yang, J., Wang, G.Y., Zhang, Q.H., et al.: ‘Optimal granularity selection based on cost-sensitive sequential three-way decisions with rough fuzzy sets’,Knowl.-Based Syst., 2019, 163, pp. 131–144

[51] Wang, J.Q., Wang, P.J., Wang, H.Y., et al.: ‘Atanassov’s interval-valued intuitionistic linguistic multicriteria group decision-making method based on the trapezium cloud model’,IEEE Trans.Fuzzy Syst.,2015,23,(3),pp.542–554

[52] Chen, S.H., Sun, W.Y.: ‘A one-dimensional time dependent cloud model’,J. Meteorol. Soc. Japan. Ser. II, 2002, 80, (1), pp. 99–118

[53] Deng, W.H., Wang, G.Y., Xu, J.: ‘Piecewise two-dimensional normal cloud representation for time-series data mining’, Inf. Sci., 2016, 374, pp. 32–50

[54] Peng,H.G.,Wang,J.Q.:‘A multicriteria group decision-making method based on the normal cloud model with zadeh’s Z-numbers’,IEEE Trans.Fuzzy Syst.,2018,26, (6), pp. 3246–3260

[55] Chen, S.M.: ‘Similarity measures between vague sets and between elements’,IEEE Trans. Syst. Man Cybern. Part B Cybern. A Publ. IEEE Syst. Man Cybern. Soc., 1997, 27, (1), pp. 153–158

[56] Chen, S.M., Chang, C.H.: ‘A novel similarity measure between atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition’, Inf. Sci., 2015, 291, pp. 96–114

[57] Hung, W.L., Yang, M.S.: ‘Similarity measures of intuitionistic fuzzy sets based on hausdorff distance’, Pattern Recognit. Lett., 2004, 25, (14), pp. 1603–1611

[58] Gorzałczany, M.B.: ‘A method of inference in approximate reasoning based on interval-valued fuzzy sets’, Fuzzy Sets Syst., 1987, 21, (1), pp. 1–17

[59] Atanassov, K.T.: ‘Intuitionistic fuzzy sets’, Fuzzy Sets Syst., 1986, 20, (1),pp. 87–96

[60] Bustince, H., Burillo, P.: ‘Vague sets are intuitionistic fuzzy sets’, Fuzzy Sets Syst., 1996, 79, (3), pp. 403–405

[61] Mendel,J.M.,John,R.I.B.:‘Type-2 fuzzy sets made simple’,IEEE Trans.Fuzzy Syst., 2002, 10, (2), pp. 117–127

[62] Wu, T., Qin, K.: ‘Comparative study of image thresholding using type-2 fuzzy sets and cloud model’, Int. J. Comput. Intell. Syst., 2010, 3, (sup01), pp. 61–73

[63] Qin, K., Li, D.Y., Wu, T., et al.: ‘Comparative study of type-2 fuzzy sets and cloud model’. Int. Conf. on Rough Sets and Knowledge Technology, Beijing,China, October 2010, pp. 604–611

[64] Liu,C.,Gan,W.Y.,Wu,T.:‘A comparative study of cloud model and extended fuzzy sets’. Int. Conf. on Rough Sets and Knowledge Technology, Beijing,China, October 2010, pp. 626–631