物流配送中多车多点路径规划算法研究
李淑飞 骆剑锋


摘 要: 物流配送中常用的Dijkstra、Floyd、A*等最短路径算法只能计算两点之间的最短路径,没有带约束条件和回程规划。多车多点路径规划算法利用神经网络对收送货地点进行分区,用百度地图API计算各点之间的最短路径,通过绕行遍历思想计算绕行贡献值,利用贪婪思想在车辆限载重、限路程的情况下组合回程,从而形成最优路径方案。该算法已用在物流企业的多车多点路径规划云平台上,大大提高了物流配送效率。
关键词: 多车多点;最短路径;绕行贡献值;规划算法;物流配送
【Abstract】: The Shortest path algorithms such as Dijkstra, Floyd, and A* commonly used in logistics distribution can only calculate the shortest path between two points, without constraints and backhaul planning. The multi-vehicle multi-point path planning algorithm uses neural network to partition the receiving and delivering places, and uses Baidu Map API to calculate the shortest path between the points,and the detour contribution is calculated by detour traversal idea, and the greedy idea is used to combine the backhaul under the condition of Limited vehicle load and distance, thus forming the optimal path scheme. This algorithm has been used in multi-vehicle multi-point path planning cloud platform of logistics enterprises, which greatly improves the efficiency of logistics distribution.
【Key words】: Multi-vehicle multi-point; Shortest path; Detour contribution value; Planning algorithm; Logistics distribution
0 引言
在物流配送活動中,物流配送路径的最优化问题,是物流配送系统优化中关键的一环。随着配送路网的日趋复杂,配送成本日益增大[1],在物流配送中规划合理的配送路线,避免迂回运输与重复运输,有利于节省配送费用,降低物流成本,提高物流配送的效率和经济效益。
物流配送问题是典型的组合寻优问题[2],常用的路径最优算法有Dijkstra[3]、Floyd、A*等算法[4]。Dijkstra算法是经典的广度优先算法,该算法的主要特点是以起始点为中心搜索所有与其连接的点,从中心向外层延展,直到延展到终点为止,因此能够有效解决单源最短路径问题[5]。Floyd算法是经典的深度优先算法,该算法利用动态规划思想,寻找给定的加权图中多源点之间最短路径,因此能够有效解决任意两点之间最短距离[6]。A*算法是基于启发式的最短路径算法,是一种静态路网中求解最短路径最有效的直接搜索方法,通过计算函数的慢相对最优解来筛选出发点周围的后继点[7]。这些算法都是求两顶点之间的最短路径,并且没有带约束条件,也没有规划回程。
现实物流配送中,可能有不同的收送货地点、不同的收送货重量,车辆也有限重、限程、限时等多条件的限制,如何合理安排车辆,使得车辆在限制负载、限制行程的情况下遍历所有客户,并且规划回程的路径方案最优,本文提出了多车多点路径规划算法。
1 多车多点路径规划算法思想
1.1 绕行遍历思想
多车多点路径规划算法主要是对多车辆在限制负载、限制行程的情况下遍历所有客户,而且还能规划回程的最短路径方案,其核心是绕行遍历思想。
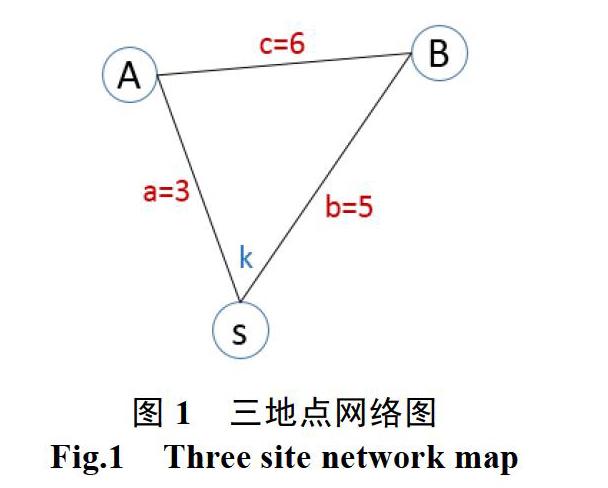
假设由S点为起始点,现在要去A、B两个地点去收送货,两地间的距离单位为km,如图1所示,求要规划回程的最短路径。
从起始点出发,要遍历所有点,并且返回起始点,路径的走法有四种:
①广播方式:S→A→S→B→S,即从S点出发到A,返回S,再从S点到B,返回S。
②往返方式:S→A→B→A→S,由S点出发,经过所有点A、B,再沿路返回。
③往返方式:S→B→A→B→S,由S点出发,经过所有点B、A,再沿路返回。
④绕行遍历方式:S→A→B→S,环绕一周,遍
历所有点,回到起始点。
表1求出了每种走法的距离及绕行贡献值。根据三角形两边之和大于第三边,可知第四种走法(绕行遍历方式)是最短路径,是最佳走法。假设把前三种走法与第四种走法的距离差称为绕行贡献值,绕行贡献值越大,越值得绕行,这是本算法的一个核心思想。
此外,还要根据S点的夹角K来判断采用广播方式、往返方式还是绕行遍历方式。当S点的夹角K为锐角,才采用绕行遍历,钝角则不绕行。
1.2 贪婪思想
本算法中,先要计算出最短距离矩阵SM、绕行贡献值矩阵RX。RX值根据筛选公式筛选出来后形成队列,并按降序存放到JXDL队列中,再逐条路径从JXDL堆栈中出栈,进入累加堆栈,累加路程值及重量值,一旦路程累加值超过限程值、重量累加值超过限重值就出栈,剔除刚进栈的路径,在网络图上按照贪婪思想连接已经出栈的路径,形成一条回程路径。
1.3 靠近原则
在组成回程时,根据收送货点是否靠近来组合回路,把相对较远的路径推后处理。是否靠近采用模糊神经网络来处理,如图2所示,假设E点与组成的回程成锐角时,可以把该地点加入回程,如果是钝角,则考虑和后面的回程组成回路。
2 多车多点路径规划算法的实现
2.1 多车多点路径规划算法的实现流程
多车多点路径规划算法具体的实现流程如下:
(1)先从数据库中读取各个收送货地点的经纬度、客户收送的货物重量以及车辆载重、车辆最大行程信息。
(2)利用模糊神经网络根据收货点与送货点的远近进行分区。
(3)利用百度地图API计算出各个地点的最短路径,再算出所有路径的绕行贡献值。
(4)对绕行贡献值筛选后形成降序路径队列,再出队,路径进入累加堆栈,入栈的时候,累加重量值及路程值;一旦路程累加值超过路程值和重量值就出栈,并剔除刚进栈的路径。
(5)利用贪婪思想根据路径是否靠近,对路径作连接处理形成回路。
(6)把规划好后的结果存储到数据库中,并且用百度地图API显示出来。
2.2 多车多点路径规划算法的实现
以物流货车收货为例,假设现有A至J的10个收货地点是在同一组,每个地点的货物重量(kg)为网络图上的结点值,L为起始点S到每个节点的矩离,D为节点间的距离。现有两种货车,分别是载重30 kg与50 kg,且货车一次行驶路程为40公里以内,图中的边权为路程(公里)。
(1)收送貨地点进行分区
根据收货点与送货点是否靠近进行分区,如果靠近,则把它们归为一类区,如果不靠近,则把收货点归成另外一类区,送货点归成第三类区。对于两点之间是否靠近的判断,则可以训练神经网络来处理。接下来对第一类的客户点进行分组,使用背包问题的解决方法进行分组:假设有n个客户点,客户点j要收货或送货的货物重量为wj(收货时wj为正值,送货时wj为负值),价格为pj(pj都为1,因为货物价格与路径规划无相关)。车辆所能承受的最大重量为W。如果限定每种货物只能选择0个或1个,用xj表示,使得。
(2)计算最短距离矩阵SM
在数据库中得到这些地点的经纬度、车辆载重和行程后,利用百度地图API算出所有结点间的最短路径,现把收送货点地图(图3)抽象成网络图(图4)。结合百度地图API和Floyd 算法[8]计算出网络图中S起点到各收货点、收货点与收货点的距离,得出收货线路最短距离矩阵SM(图5)。
(3)计算绕行贡献值RX
计算完各结点间最短路径之后,接下来就要求出哪一条路径最适合绕行,根据绕行遍历思想,用绕行公式RX(i,j)=SM(i,0)+SM(j–1,0)–SM(i,j)求出绕行贡献值[9](图6),绕行贡献值越大,路径越短,越值得绕行。
(4)对绕行值RX进行筛选
每组成一个回程,则对第二类客户点与现有的回程作是否靠近的判断,如果靠近的话,则用插入路径方法,插入经过此客户点的路径。重复此操作,直到所有结点访问完毕。这样根据绕行思想和贪婪思想,逐步组合好了规划路径,最后通过百度地图API把这些路径显示在地图上。
3 结语
本算法是针对多辆车到多个地点的最短路径问题,在算法中利用神经网络对地点按远近进行分区,利用百度地图API计算出各个地点的最短路径,根据绕行遍历思想算出所有路径的绕行贡献值,再用贪婪思想把路径组合起来,最后把规划好后的结果存储到数据库中,并且用百度地图API显示出来,使得在物流配送中能够满足车辆不超重、不超程并规划回程的路径最短。该算法已用在物流企业的多车多点智能路径规划云平台,也可以广泛应用在物流企业、公交路线规划、旅游规划、无人驾驶等各个行业。
参考文献
[1]钮亮, 张宝友. 基于云计算求解城市物流配送最短路径研究[J]. 科技通报, 2015(5): 184-188.
[2]李晶, 闫军. 基于Dijkstra算法和Floyd算法的物流运输最短路径研究[J]. 科技信息, 2012(2): 575-576.
[3]王华. 基于Dijkstra算法的物流配送最短路径算法研[J]. 计算机与数字工程, 2011(3): 48-50.
[4]高小芳. 物流配送最优路径规划[D]. 福建: 华侨大学, 2016.
[5]叶颖诗, 魏福义, 蔡贤资. 基于并行计算的快速Dijkstra算法研究[J]. 计算机工程与应用, 2019, 7.
[6]吴海峰. 最短路径算法——Dijkstra及Floyd算法[J]. 中国新通信, 2019, 21(02): 32-33.
[7]魏为民, 陆致静, 叶语. 一种基于A*算法改进的最短路径搜索方法[J]. 上海电力学院学报, 2018, 34(02): 180-184.
[8]张陈翔. 基于Floyd算法的校园导航应用程序开发[J]. 软件, 2018, 39(4): 83-85.
[9]骆剑锋, 陈俞强, 郑东瀚. 智能交通通信同心游程路由算法[J]. 控制工程, 2016, 6(06): 975-978.

