一种改进的数据场聚类算法

郜丽鹏，沙作金

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

在现代电子战中，随着科学技术的不断更新应用，新的雷达体制和信号调制样式相继出现在日益复杂的电磁环境中[1]。雷达信号分选作为衡量侦察系统是否仍能适应当前电子对抗环境的标志[2]，面临着日益严峻的挑战。如何在现在这种复杂的电磁环境中正确地分选出雷达信号，一直是分选工作中的重点和难题。

目前电磁环境中的雷达脉冲数量已经超过了每秒百万个的量级，而雷达分选算法需要进行处理的数据量和雷达数目的平方呈正比例关系，而分选设备处理速度的提升受限于硬件设备[3]，因此有必要减轻主分选算法的负担，将聚类作为雷达信号的预处理过程可以很好地达到这个目的。K−means聚类算法作为一种经典的聚类算法，原理简单，收敛速度快，因而被广泛应用[4]，不过该算法的缺点也较多，对噪声敏感、需要人工设置K值大小、聚类效果受初始聚类中心的选取影响等。李德毅[5]院士在传统物理场的思想上提出了数据场这一概念之后，数据场被应用到雷达信号聚类算法中，能够克服K−means聚类算法的这几个缺点，具有良好的应用性能。因此，本文提出一种基于数据场的雷达信号聚类算法，计算每个数据对象在数据场中的势值，根据势值的极值点求出势心，势心就是雷达信号的参数中心。作为聚类的聚类中心，势心的数量则是聚类的类别个数，因此无需人工设置聚类数目的值以及选取初始聚类中心。此外设置数据点的势值阈值可以将孤立的噪声点剔除出去。针对聚类过程中出现的增批现象，将数据场的场强函数的形式进行改进，取得了良好的效果。

1 数据场聚类

1.1 数据场

将数据对象的集合映射到数域空间中，依照物理学中的稳定有源场，将数据对象视为源点，在源点周围产生场，对周围其他的数据对象产生影响，能够影响的范围所构成的空间就成为数据场[6]。

1.2 场强函数

为了能够准确描述数据场是如何对周围的数据对象产生影响、相互之间进行作用的，参考物理中的牛顿万有引力定律和库伦定律公式[7]，数据场也应该存在一种方式可以衡量数据场中的源点对周围其他数据对象的影响强弱的函数公式，则定义这个公式为场强函数。数据场的场强函数是描述以源点为中心的周围空间中的数据场的变化规律的函数，考虑到高斯分布的普遍适用特性，概率密度分布函数的形式以及短程场作用更方便表达数据对象分布的聚簇的特性，场强函数一般定义为[8]

1.3 势函数

一个数据对象的场强函数描述的是以其为源点的数据场的变化规律，但是数据挖掘面对的是大量的数据对象，只研究单个数据对象的数据场变化规律对整个数据集合并没有什么实际意义，需要研究的是所有数据对象的数据场的共同作用下的空间中的点的场强值的变化规律。定义此点处的所有数据场的场强值的和为势值，根据这个定义和场强函数可以得到势函数的公式为[10]

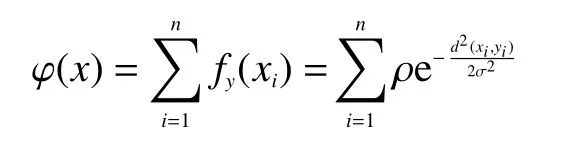
式中n表示为数据的数量。

1.4 辐射因子

图1 辐射因子不同时势值变化

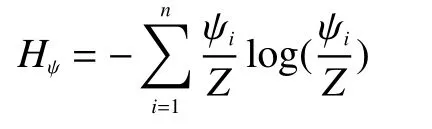
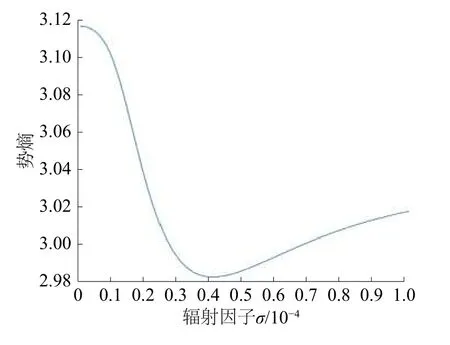
图2 辐射因子与势熵的关系曲线

1.5 剔除孤立噪声点

孤立噪声点距离实际的聚类中心有相对很大的距离，这个距离已经远远超出了单个数据点的数据场所能有效辐射的范围，即距离远远大于[13]。根据数据场的场强函数可以得知，在这个距离下，其他脉冲点辐射给它的场强的大小的数量级远远小于这个数域空间中存在的脉冲个数的数量级，所以孤立脉冲点的势值大小应该大于并且十分接近1。因此可以设置阈值，将势值小于阈值的数据对象视为噪声剔除掉。

2 改进的数据场聚类

除了要满足场强函数的导数值在近距离时比高斯函数要小之外，还要满足场强函数的其他特点：场强函数是一个连续光滑的函数、在距离为0时，场强值为0；距离趋于无穷大时，场强值趋于0。根据上述几个条件，最先想到的就是指数函数。

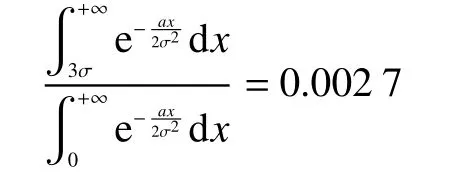
解这个方程，得到：

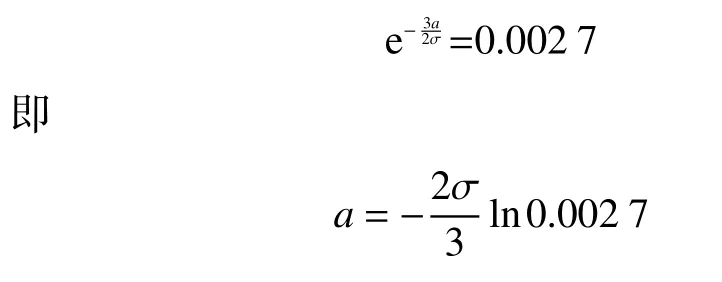
在实际中，a的值可以根据情况进行调整。

综上所述，改进的的场强函数的表达式为

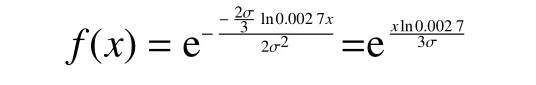
改进的数据场聚类的步骤为：

1）对提取聚类所用的3个参数脉宽(PW)、载频(RF)、到达角(DOA)进行归一化处理；

2）将脉冲序列按照到达时间排序，依次计算各个脉冲点之间的欧式距离，得到一个n×n的距离矩阵；

3）将所求得的距离矩阵代入数据场的场强函数，得到各个脉冲点的场强值，按列求和得到每个点的势值。

4）根据设置的阈值剔除孤立噪声点，找到局部势值最大的数据样本作为聚类中心，局部势值最大的数据样本的个数作为聚类数目；

5）根据之前求得的距离矩阵，将雷达脉冲序列中的数据样本依次划分到距离此数据样本最近的一个聚类中心的那一类中[14]。

3 算法仿真

3.1 求解聚类中心

本文仿真了12部雷达脉冲信号，参数如表1所示。表中序号1~5为常规雷达信号，序号6、7为抖动雷达信号，序号8~10为参差雷达信号，序号11、12为捷变频雷达信号，分别是脉间捷变和脉组捷变雷达信号。雷达信号脉宽精度为1 μs，载频精度为1 MHz，方位角精度为1°，10%的干扰脉冲。图3为仿真的12部雷达信号在以载频−脉宽−到达角为参数的的三维空间中的分布。

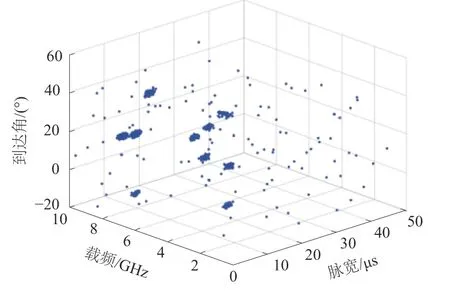
图3 待聚类雷达信号

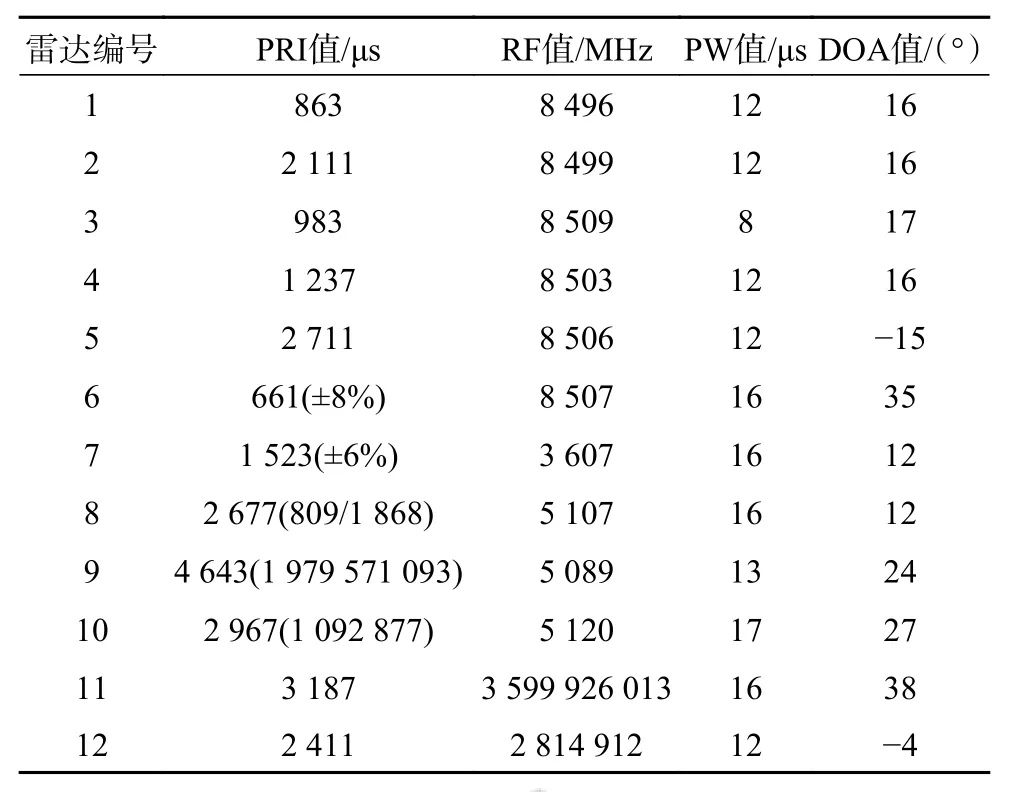
表1 雷达参数表

计算所有雷达脉冲信号的势值，可以得到雷达脉冲信号的脉宽、载频、到达角和势值的关系图如图4~6所示。

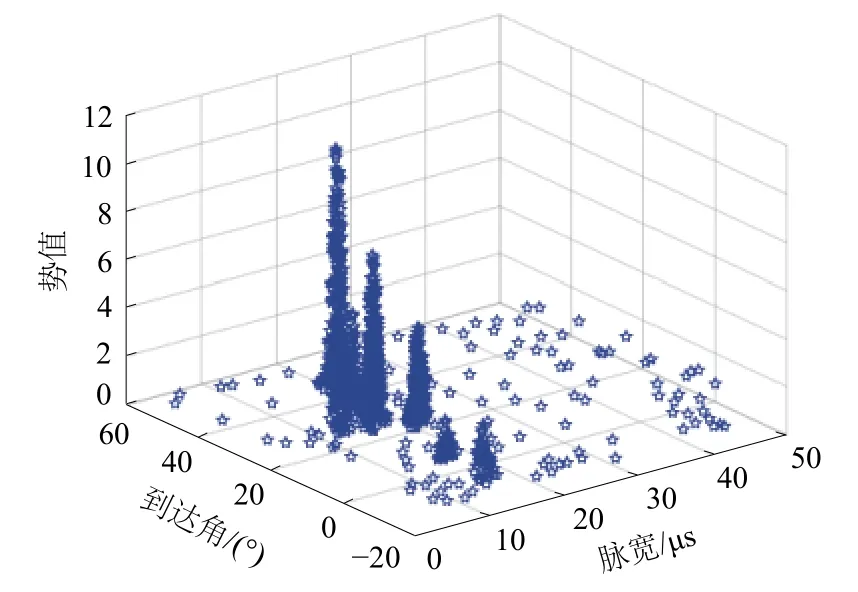
图4 脉宽−到达角−势值关系

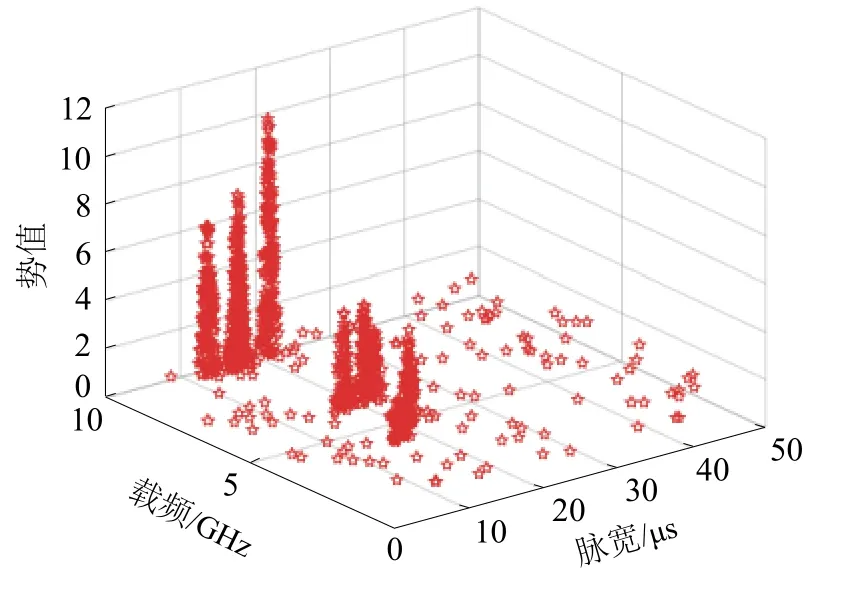
图5 脉宽−载频−势值关系

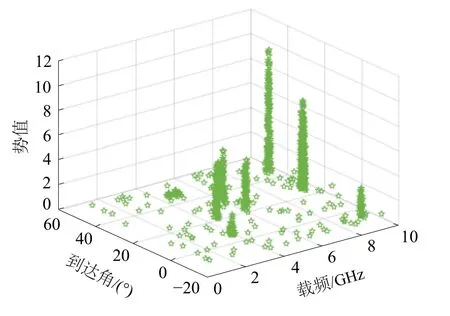
图6 载频−到达角−势值关系

使用剔除势心法得到的聚类中心如表2所示。

表2 聚类中心参数表

3.2 改进前后的数据场聚类对比

将改进前后的数据场聚类求得的聚类中心与理论的雷达信号中心进行误差值的计算，并进行1 000次的蒙特卡洛实验，仿真结果如图7所示。

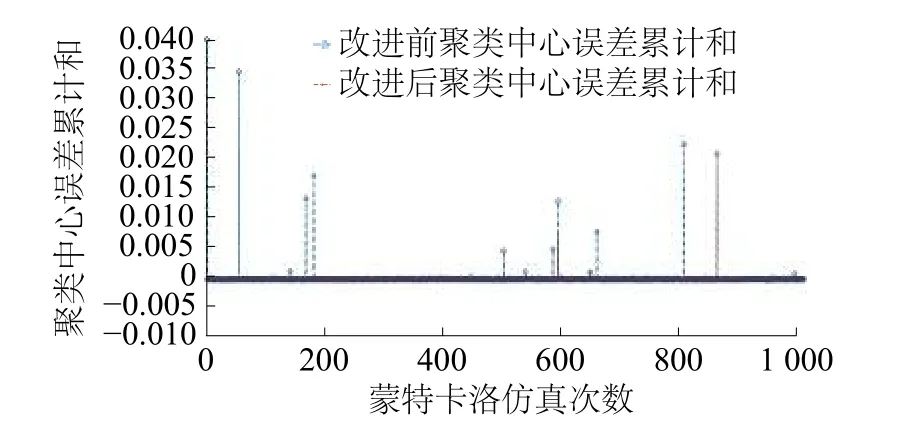
图7 改进前后的聚类中心误差曲线

可以看到改进前的数据场聚类会出现多次求得的聚类中心与理论值的误差很大的情况，而改进之后的数据场所求得的聚类中心与理论值的误差的平均值和方差都要比改进前小。分析出现误差大的情况是因为出现了增批的现象，改进的数据场聚类有效地抑制这种增批现象的出现。

4 结论

本文提出了一种改进的数据场聚类算法，通过重新分配数据场内场强值和距离的关系变化情况，即对场强函数进行改进这一方式达到改善聚类结果的目标。

1）改进后的数据场聚类求得的聚类中心与理论值的误差和方差更小，说明求得的聚类中心更准确；

2）改进后的数据场聚类出现增批现象的次数大大减少。

经仿真实验表明，本文提出的算法能够很好地完成聚类，具有良好的聚类性能。关于如何减少出现的漏批现象还需要进一步的深入研究。