A Parametric Study of Mesh Free Interpolation Based Recovery Techniques in Finite Element Elastic Analysis

Mohd.Ahmed,Mohamed Hechm i El OuniDevinder Singh and Nabil Ben Kahla

1College of Engineering,Main Campus,Gregar,K.K.University,Abha,61421,KSA.

2Minitry of Information,Soochan Bhavan,CGO Complex,Delhi,110003,India.

Abstract:The paper presents a parametric study on interpolation techniques based postprocessed error estimation in finite element elastic analysis by varying important parameters of recovery,interpolation scheme and type of patch construction.The quality of error estimation with recovery parameters is compared in terms of local and global effectivity of error estimation,rate of error convergence,and adaptively refined meshes.A mesh free moving least square interpolation technique with proven reliability and effectivity is introduced for improving the recovery of finite element solution errors.The post-processed finite element solutions of elastic problems are presented for performance study under different parameters of recovery technique.The study concludes that recovery parameters of interpolation method have pronounced effect on the recovery of finite element solution error and analysis in adaptive environment.

Keywords:Effectivity,error norm,moving least square interpolation,least square interpolation,recovery techniques.

1 Introduction

The finite element method yields approximate solutions for the problems and the errors are inherent in the method.The finite element error is of two types namely,discretization and elemental error [Dow (1999)].Elemental errors arise from modeling deficiencies in individual elements.They depend upon the algorithm employed for solving system equations and the method employed for computing derivatives of state variables.Elemental error can produce serious error in the computed solution unless special care is taken.The discretization errors are produced because the sub regions are not capable of representing the full range of behavior of the continuum.The discretization errors manifest themselves as discontinuities or jumps in components of stress or strain between elements and as misrepresentation of the actual boundary stresses.The magnitude of the jumps is indicative of the size of the local discretization error.The latter can be identified by whether the finite element solution satisfies equilibrium conditions at every point of the problem domain.The discretization error can be reduced by increasing the number of elements.The discretization error can be assessed by various developed estimation techniques.However,interpolation techniques based error estimation is most popular that rely upon the so-called “recovery” of a higher order approximation of the computed variable of interest.The development of recovery of solution errors,a-priori and aposteriori-error estimation techniques are underway for the last several years.An extensive survey of a-posteriori error estimation is due to Ainsworth et al.[Ainsworth and Oden (1997);Gratsch and Bathe (2005);Ainsworth and Oden (1997);Gratsch and Bathe (2005)].Mirzaei [Mirzaei (2015)] provides a comprehensive analysis of error estimation considering moving least square approximation.An error estimation method based on side curvature has been presented by Xing et al.[Xing,Wang and Makinouchi (1999)].It was used to estimate the accuracy of finite element discretization of a deformed sheet,especially one with sharp or quasi-sharp corners.Liu et al.[Liu and Elmaraghy (1992)] discussed discretized errors,and their estimation in conjunction with quadrilateral finite element meshes which are generated by an intelligent mesh generator.Zienkiewicz et al.[Zienkiewicz and Zhu (1987)] proposed an error estimator which is not only accurate but whose evaluation is computationally so simple that it can be readily implemented in existing finite element codes.The estimator computes energy norm of error on global as well as local levels.Liu et al.[Liu,Nguyen and Lam (2008)] have proposed technique to obtain the exact finite solution to mechanics problem using the alpha finite element method (αFEM).Kim et al.[Kim and Lee (2010)] applied the equilibrated residual method with set of Neumann data for nonconforming elements to improve the finite element linear elasticity solution.Ullah et al.[Ullah,Coombs and Augarde (2013)] proposed a coupled finite element method (FEM) and the element-free Galerkin method (EFGM) error estimation based on local maximum entropy shape functions,for linear and nonlinear problems.Many different post-processing techniques can be employed to improve the quality of the derivatives of the finite element approximations such as averaging [Bramble and Schatz (1977)],local or global projections [Hinton and Campbell (1974)],and those exploring the super-convergence phenomenon.The nodal average method is a simple technique that leads to optimal convergence rates when only linear elements are considered.A general recovery technique has been developed by Zienkiewicz et al.[Zienkiewicz and Zhu (1992)] for determining the derivatives.The implementation of the recovery technique is simple and cost effective.The technique has been tested for a group of linear,quadratic and cubic elements for both one and two dimensional problems.Numerical experiments demonstrate that the recovered nodal values of the derivatives with linear and cubic elements are super-convergent.One order higher accuracy is achieved by the procedure with linear and cubic elements but two order higher accuracy is achieved for derivatives with quadratic elements.In particular,an O(h4) convergence of the nodal values of the derivatives for a quadratic triangular element is reported.Zienkiewicz et al.[Zienkiewicz and Zhu (1992)] derived a theorem on dependence of the effectivity index for the Zienkiewicz-Zhu error estimator and the convergence rate of a recovered solution.They found that with super-convergent recovery,the effectivity index tends asymptotically to unity.Numerical tests on various element types illustrate the effectivity of their error estimator in the energy norm and pointwise gradient (stress) error estimation.Li et al.[Li and Wiberg (1994)] presented a post-processing technique for obtaining a-posteriori error estimators both in the energy and L2norms,an element patch that represents the union of the considered element and its neighbours is introduced.The post-processing for determining more accurate solutions is made by fitting a higher order polynomial expansion to the computed solution at super-convergent points in the patch.The element error estimate norms are calculated directly from the improved solutions.The recovery by equilibrium in patches (REP) and the recovery by compatibility in patches (RCP) to obtain the improved stresses to the computed stress are due to Ubertini [Ubertini (2004)].Parret et al.[Parret-Fréaud,Rey,Gosselet et al.(2016)] propose a moving least squares (MLS) recovery-based procedure to obtain post- processed smoothed stresses field in which the continuity of the recovered field is provided by the shape functions of the underlying mesh.Sharma et al.[Sharma,Zhang,Langelaar et al.(2018)] propose a stress recovery procedure for low-order finite elements in 3D in which the recovered stress field is obtained by satisfying equilibrium in an average sense and by projecting the directly calculated stress field onto a conveniently chosen space.More recently,Ahmed et al.[Ahmed,Singh and Deshmukh (2018)] has effectively implemented the element free Galerkin based recovery technique in finite element analysis of elastic problems with super-convergent properties.The researchers also present the improvement in the finite element method.Bathe et al.[Bathe and Zhang (2017)] has proposed a new finite element solution scheme with overlapping elements and present its complete formulation for twodimensional problems.Aragon et al.[Aragon and Simone (2017)] proposes a Discontinuity-Enriched Finite Element Method (DEFEM) for modeling problems with both weak and strong discontinuities independently of the finite element discretization and which adds enriched degrees of freedom only to nodes created at the intersection between a discontinuity and edges of elements in the mesh.

The finite element analysis coupled with post-processing technique is influenced by several recovery parameters (i.e.,parameters affecting the post-processed results) including meshing scheme,post-processed field variable,error norm,interpolation type for post processing,shape and size of influence domain,dilation parameter,order of polynomial expansion in basis function,weighting function,etc.There are only a few published works on the role of recovery parameters in interpolation based post-processed finite element procedures.Rajendran et al.[Rajendran and Liew (2003)] have proposed best-fit approach for predicting optimal stress sampling points for the patch recovery of nodal stresses.Wang et al.[Wang and Liu (2002);Kanber,Bozkurt and Erklig (2013);Wang and Liu (2002);Kanber,Bozkurt and Erklig (2013)] have propose optimal shape parameters in uniform grids while Perko et al.[Perko and Sarler (2007)] proposes shape parameters optimization in non-uniform grids.Neil et al.[Neil,Atluri and Zuo (2006)] propose a practical mathematics model for obtaining the optimal radius of support of radial weights used in MLS methods.Onate et al.[Onate,Perazzo and Miquel (2001)] have discussed the completeness,robustness,continuity and accuracy aspect of moving least squares (MLS) interpolation procedure.The present work deals with the study of influence of parameters on interpolation recovery based finite element elastic analysis.The moving least squares (MLS) interpolation technique is introduced very recently for post-processing of finite element solutions,it will be interesting to quantify the effect of various factors of MLS interpolation on the error recovery process,Moreover,presently post-processed techniques use mesh reliant patches for recovery of discretization error in the finite element solution.The meshes less patches for interpolation are investigated in the present study.The discretization error at element and global levels in the finite element solution are presented in energy norm and elemental error in the solution is assumed constant with insignificant effect.The linear and quadratic triangular elements schemes are used for problem domain discretization.The four recoveres parameter namely,interpolation type for post-processing,shape of support domain,dilation parameter and order of polynomial expansion in basis function are selected for the parametric investigation.The effect of application of error estimation techniques under different recovery parameters are also explored for finite element analysis in adaptive environment.

2 Least square interpolation technique (Zienkiewicz-Zhu (ZZ) Recovery)

In ZZ super-convergent patch recovery technique [Zienkiewicz and Zhu (1992)],the nodal values of stress belong to a polynomial expansion of the same complete order as that present in the basis function and is valid over a patch of nodes surrounding the particular given node.Following polynomial expansiosn may be used for each co mponent of stress.

σ*(X) = P(X).a in which P(X) is the basis of the assumed polynomial,X = (x1,x2),the spatial variable and a the vector of the unknown parameters.

A least square fit of σshvalues over the nodal patches may be made by minimizing the functional

On simplification,it results into the following equation.

3 Moving Least Squares (MLS) interpolation recovery technique

The interpolation recovery technique derived the approximate functions using a set of nodes distributed over a domain,without depending on the meshing scheme,in least square sense.The Moving Least Square (MLS) approximation,uh(x),can be defined as,uh(x) =whereφ(x) is shape function and m is the total number of terms in the basis function P(x).In the present study,m is taken as six for linear and nine for quadratic elements.PT(x) = [1,x,y,x2,xy,y2]is taken for linear element andPT(x) = [1,x,y,x2,xy,y2,x2y,xy2,x2y2]is taken for for quadratic element.Theφ1 (x)is given as,φi(x)=PT(x)a-1(x)P(xi)w(x-xi).The vector of coefficients a(x) can be obtained by minimizing a weighted residual as,xi)[PT(xi)a(x)-uiℎ]2where n is the number of nodes i and w(x-xi) is a weight function in 2-D associated to each node (domain of influence of that node) which is usually built in such a way that it takes a unit value in the vicinity of the point where the function and its derivatives are to be computed and vanishes outside a region Ωi surrounding the point xi.The support of the shape function φ1(x) is equivalent to the support of the weight function.The following cubic spline weight function with circular or rectangular domain of influence is considered in the present study.

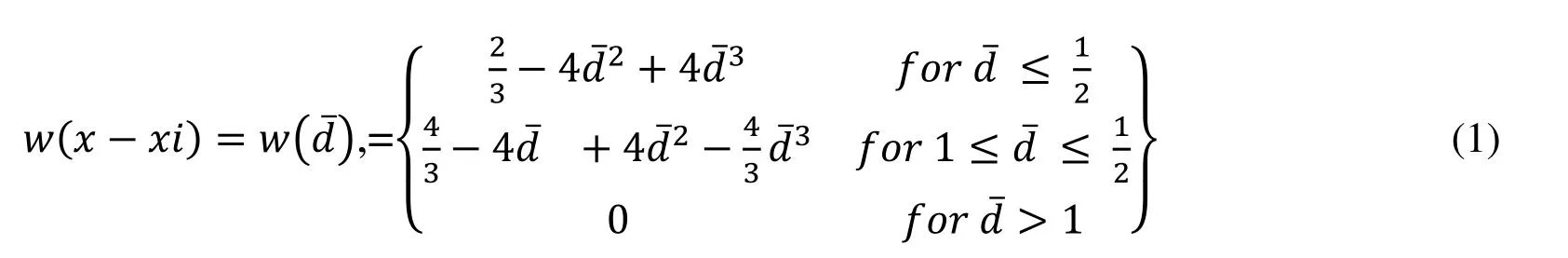
Minimization of weighted residual leads to φ (x)=PT(x)a-1(x)B(x)w(x-xi)φℎwhere a(x)=and B(x)=[wi(xxi)P(xi),……,….wn(x-xn)P(xn)]

By putting MLS shape function into the well-known form of shape function equation,we get,φ (x)=NT(x)φℎin which NT(x)=PT(x)a-1(x)B(x)w(x-xi)φℎ.

4 Error evaluations

The error in computed stress (σ),eσ*(σ- σh) is defined as the difference between the exact or (recovered) values (σ) and respective finite element solution value (σh).

The errors can be quantified in appropriate norms.The error in energy norm (E) may be defined as,‖e‖E=[eσ∗TDeσ∗dΩ]1/2An estimator is asymptotically exact for a particular problem if the global and local (element) effectivity indexi.e.,ratio of the exact error (‖eex‖) and the evaluated error estimate (‖e‖) in energy norm,converges to one when the mesh size approaches to zero.

The accuracy (η) of a finite element solution may be defined as,The solution is acceptable if η ≤ ηallow where ηallowis the allowable accuracy.If not,h-refinement i.e.,reduction of element size is needed.

5 Parametric study of interpolation recovery technique

Numerical experiments on plate problems using finite element method were carried out to study the effect of the recovery parameters (i.e.,parameters affecting the post-processed results) in terms of effectivity,rate of convergence and adaptively refined mesh.The plate domain is discretized using linear and quadratic triangular elements.The error at element and global levels in the finite element solution are computed in energy norm.The effect on the performance of interpolation recovery based post processed technique is studied by varying four parameters namely,interpolation type for post-processing,support domain shape,dilation parameter and number of terms in basis function.The mesh free circular and rectangular support domain shape is used in MLS interpolation recovery technique.The mesh dependent node patch is also used for least square and MLS interpolation.Six different dilation parameters namely,2.4,3.0,4.0,4.5,5.5 and 6.5,are selected for the moving least square interpolation formulation with consideration to order of element.Two set of number of basis function terms namely,3,6,9 and 6,9 10 are selected for fitting the derivatives of field variable over the nodes in support domain to recover the solution error in linear and quadratic element respectively.

5.1 Elastic analysis of plate problem

The square elastic plate problem subjected to body loads (bx,by) is tested to study the effect of recovery parameters on post-processed finite element analysis of the problem.The body force of the plate is in the form of polynomials and close form displacements solution (u,v) due to body load are given in Eqs.(2) to (4) [Zienkiewicz and Zhu (1992)].The plate domain discretized with linear and quadratic triangular elements is employed in the analysis (Fig.1).

where constants α and β are α=[E.ν/((1- 2.ν) .(1+ ν))],β=[E/(2.(1+ ν))],and E and ν are Modulus of elasticity and Poisson’s Ratio respectively with a value of 1.0 N/mm2and 0.3.

Figure 1:Plate problem discretized with triangular elements

5.1.1 Recovery parameter:interpolation technique type and patch construction

Two types of interpolations formulation namely,least square (ZZ recovery) interpolation and moving least square (MLS) interpolation,for fitting the field variable or its derivatives over the mesh reliant and mesh free patch of nodes,are used in recovery based finite element parametric study.The mesh dependent node patch for interpolation is the patch of nodes surrounding the particular given node of the mesh as shown in Fig.2.The mesh dependent node patch is considered for MLS and least square interpolation.The MLS interpolation technique uses mesh free patch,i.e.,support domain in circular and rectangular shape.The interpolation formulation effect on post processed results is investigated keeping dilation parameter constant with a value of 3.0 and 4.5 for linear elements and quadratic elements respectively.The number of terms in polynomial basis is taken as 6 for linear elements while the number of terms is 9 for quadratic elements in MLS interpolation technique.Tabs.1-4 give the error convergence and effectivity obtained in post processed finite element elastic analysis using least square (ZZ) interpolation and MLS interpolation based recovery for linear elements.The finite element elastic analysis results with node patch and support domain constructed from the meshes of quadratic elements are given in Tabs.5 to 8.

From the tables,Tabs.1-8,it is clear that recovery parameter,interpolation techniques and,types of element and patch construction significantly affect the performance of postprocessing based finite element analysis.The tables depict that order of error obtained employing recovery procedures is much lower than FEM solution error and error convergence is also manifold as compared to the FEM solution error with reduction of mesh size.The effect on error order and convergence is further enhanced for higher order elements.The MLS interpolation recovery performs better over least square interpolation recovery with different elements and patch types giving higher error convergence and effectivity converging nearly to one with increase in mesh fineness.As far as the performance of element and patch type is concerned,the overall performance of lower order element and mesh free node patch (support domain) is superior.When comparing the support domain shape effect on the post-processed analysis,the rectangular support domain construction has better performance as compared to circular shape of support domain for both lower and higher order element.The convergence rate is higher and the effectivity is closer to one in case of rectangular support domain.Though,the order of error in energy norm obtained is higher in rectangular support domain.

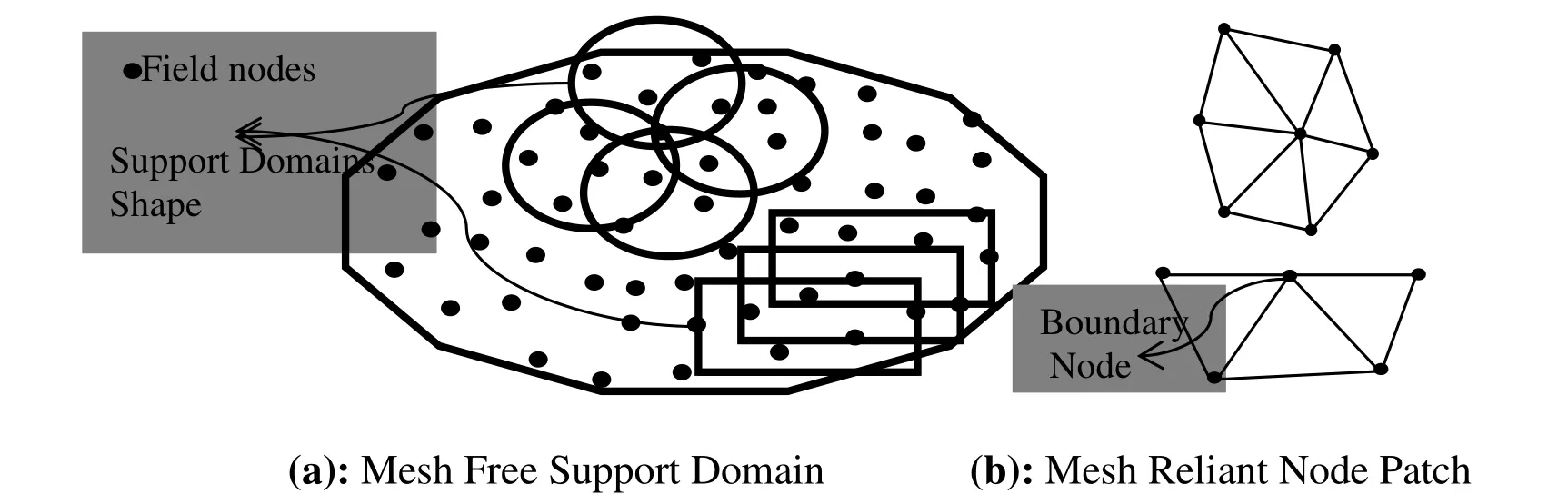
Figure 2:Support domains and node patch for interpolation based recovery technique

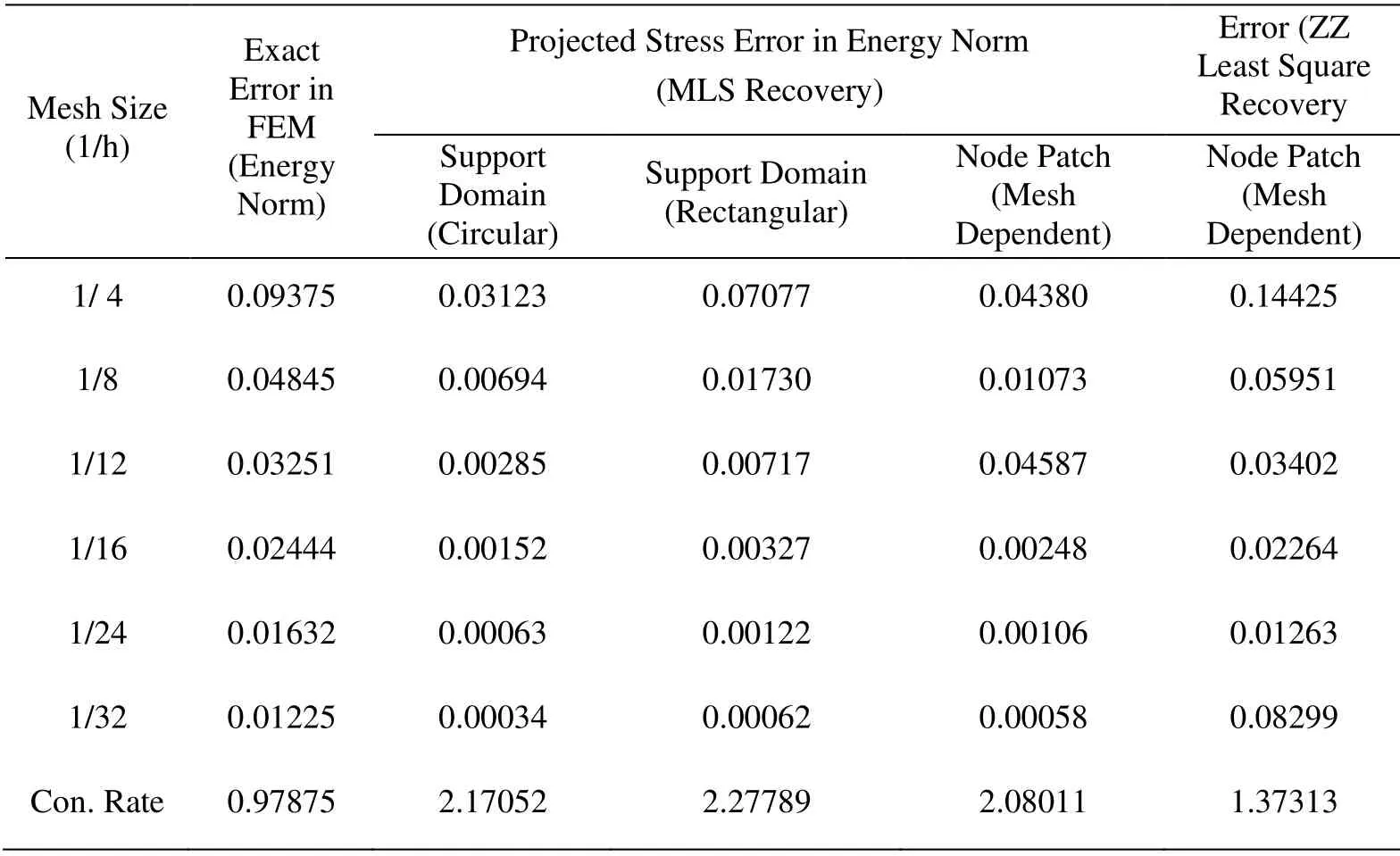
Table 1:Predicted errors for square plate problem with interpolation type and node patch in post-processing techniques (linear structured)

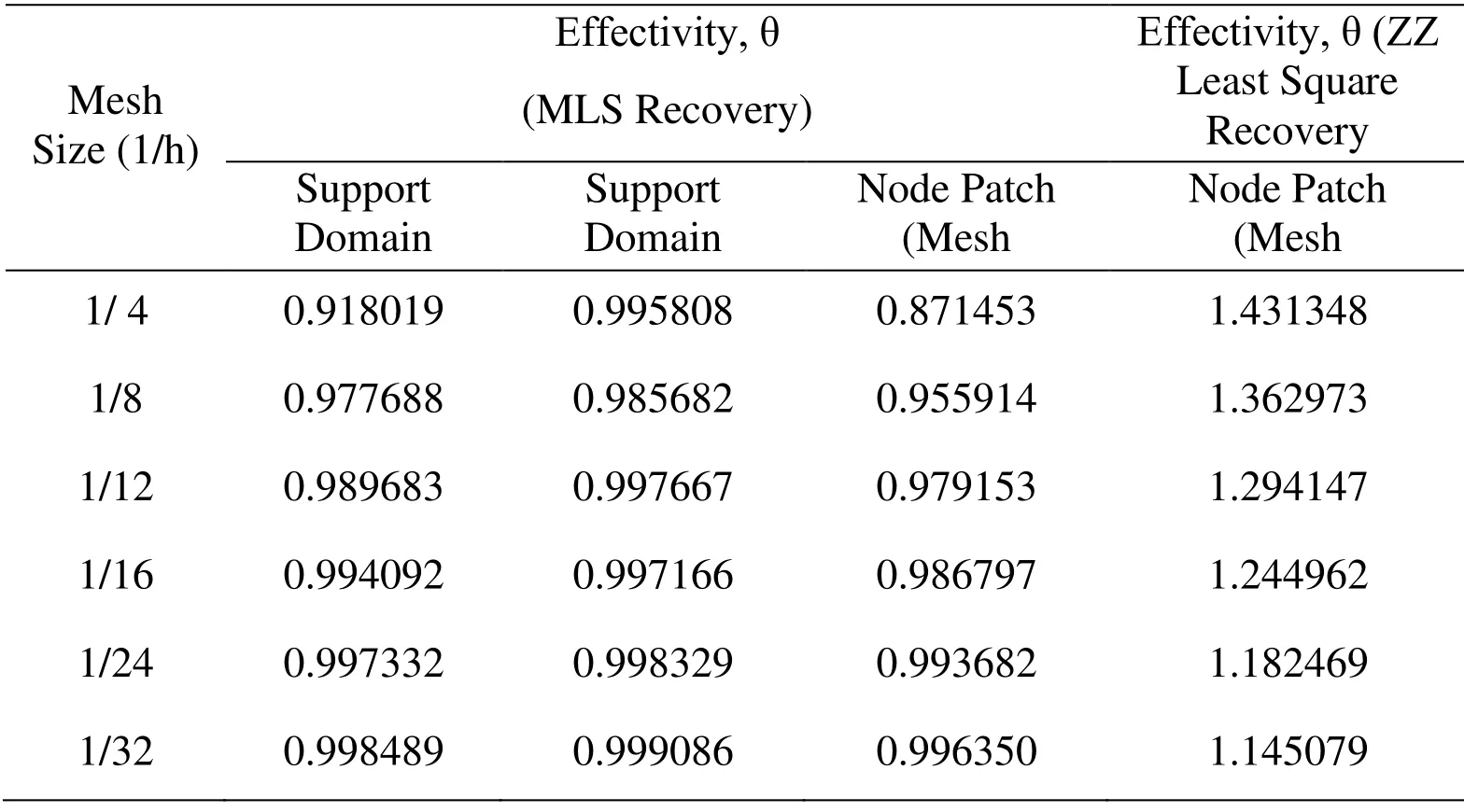
Table 2:Global effectivity for square plate problem with interpolation type and node patch in post-processing techniques (linear structured)

Table 3:Predicted errors for square plate problem with interpolation type and node patch in post-processing techniques (linear unstructured)

Table 4:Global effectivity for square plate problem with interpolation type and node patch in post-processing techniques (linear unstructured)

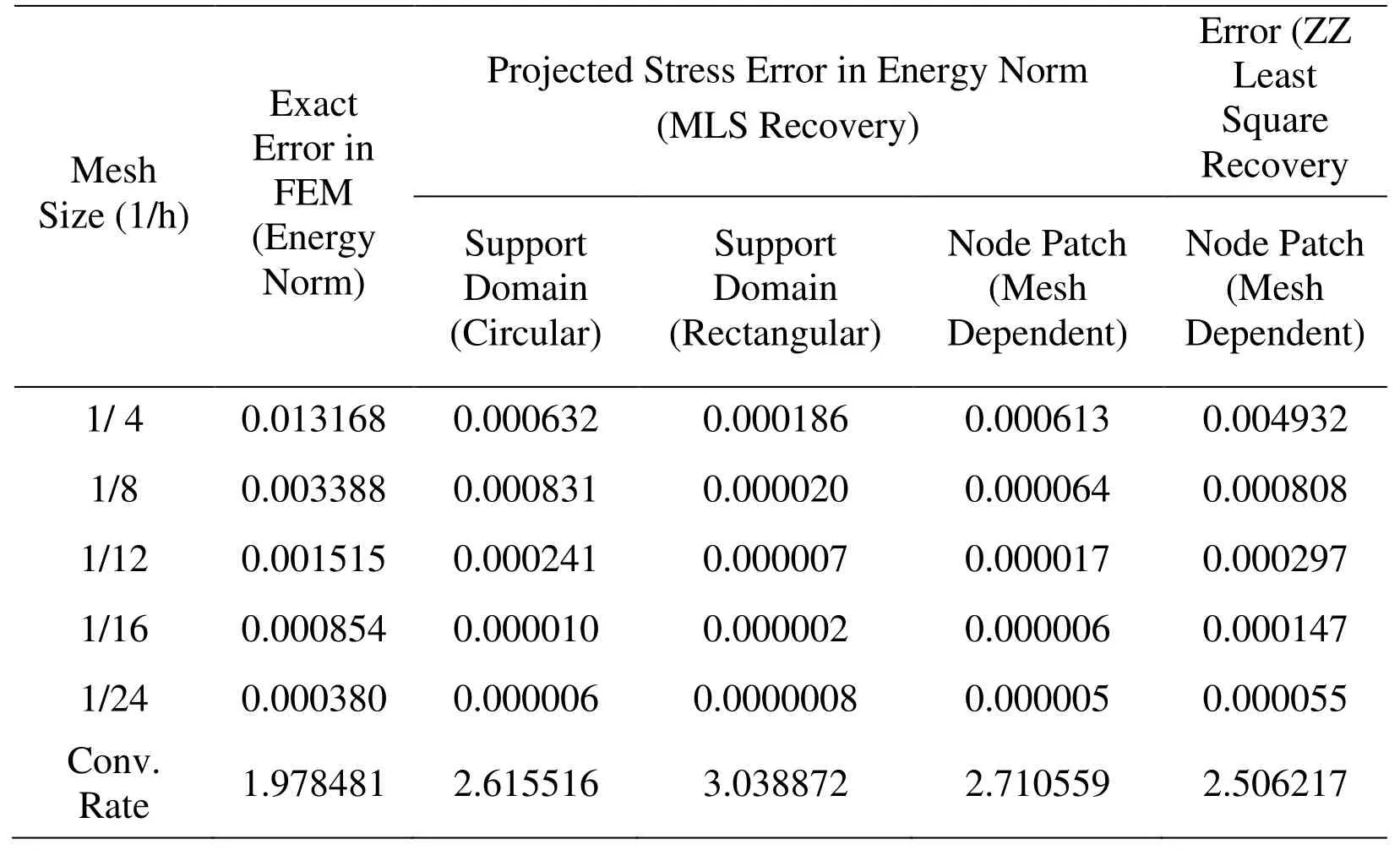
Table 5:Predicted errors for square plate problem with interpolation type and node patch in post-processing techniques (quadratic structured)

Table 6:Global effectivity for square plate problem with interpolation type and node patch in post-processing techniques (quadratic structured)

Table 7:Predicted errors for square plate problem with interpolation type and node patch in post-processing techniques (quadratic unstructured)

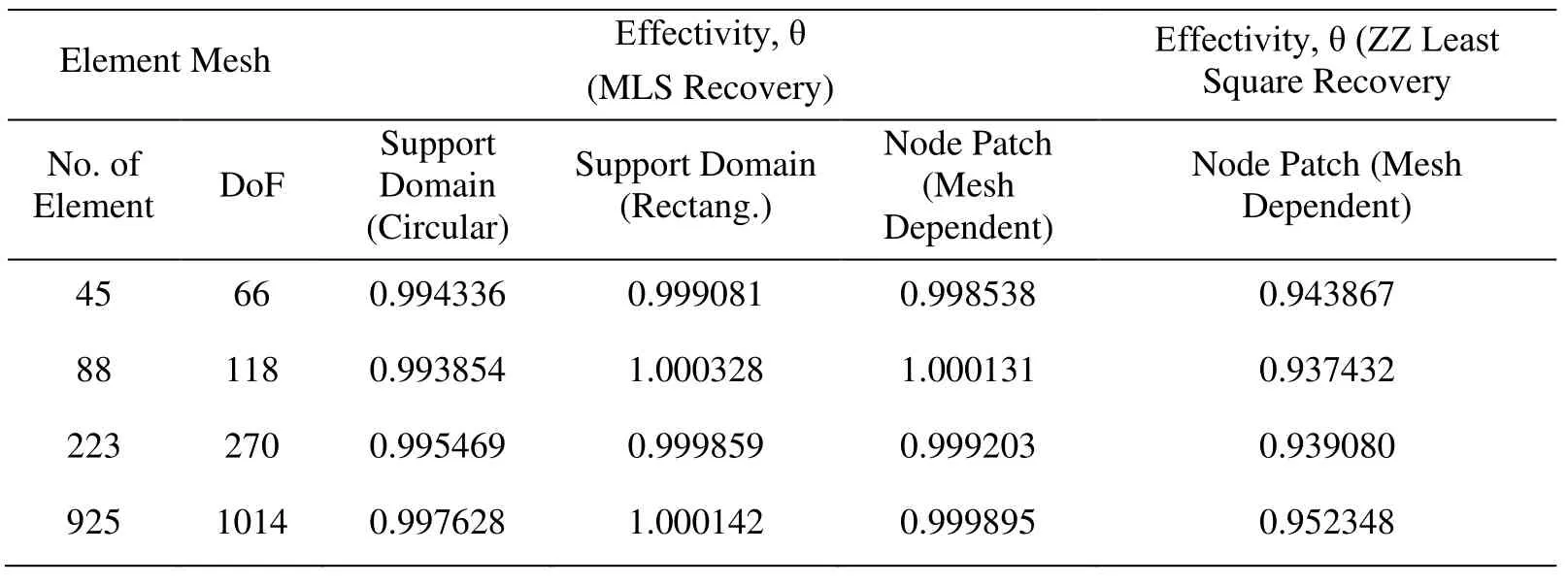
Table 8:Global effectivity for square plate problem with interpolation type and node patch in post-processing techniques (quadratic unstructured)

The element effectivity frequency and stress error distribution in plate problem domain obtained with different recovery parameters is also plotted.The element effectivity frequency for linear and quadratic elements for support domain shape used in MLS interpolation based recovery technique is plotted in Fig.3 at last refinement level considered.The effectivity frequency plots using mesh reliant patch ZZ recovery,mesh reliant patch MLS recovery and mesh free patch (support domain) based MLS recovery technique in recovery based finite element analysis are shown in Fig.4.The Fig.3 and Fig.4 depicts that unstructured discretization with higher order elements is more sensitive to patch construction type in comparison to low order elements as the effectivity results for the analysis is similar for lower order elements.The least square interpolation recovery using mesh dependent patch using higher order element perform better than MLS interpolation recovery.

The stress error distribution obtained with interpolation based recovery in plate domain using different patch construction type and structured/unstructured mesh are plotted in Fig.5 and Fig.6.It is evident that the error pattern over problem domain is clearly distinct for different patch construction type and structured/unstructured mesh.The error distribution using recovery considering unstructured mesh seems to be more evenly distributed than error distribution using structured mesh.Also,error recovery using higher order element become further smooth and problem domain is divided two separate zone of lower and higher order error.The error distributions plots for different recovery parameters show that the error distribution patterns for exact and recovered error distributions in plate domain are in good agreement.However,the order of errors is different with different recovery parameters.

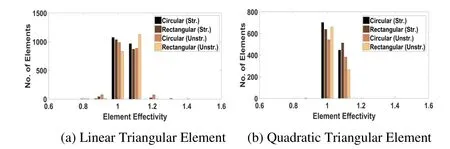
Figure 3:Histogram-element effectivity vs. number of elements for plate problem using different shape of support domain in mls interpolation based post-processed finite element analysis

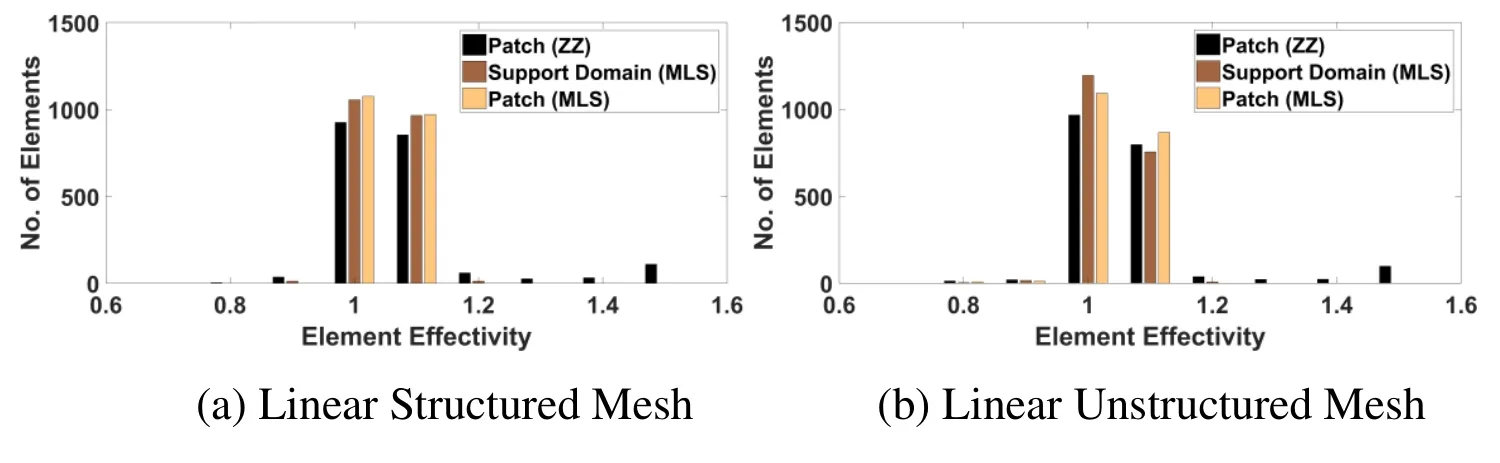
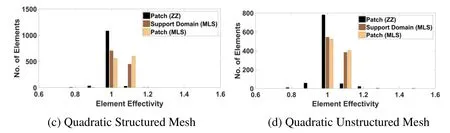
Figure 4:Histogram-element effectivity vs. number of elements for plate problem using different interpolation and patch construction type in recovery based FE analysis [structured mesh at size =1/32 &unstructured mesh at 1978 elements]

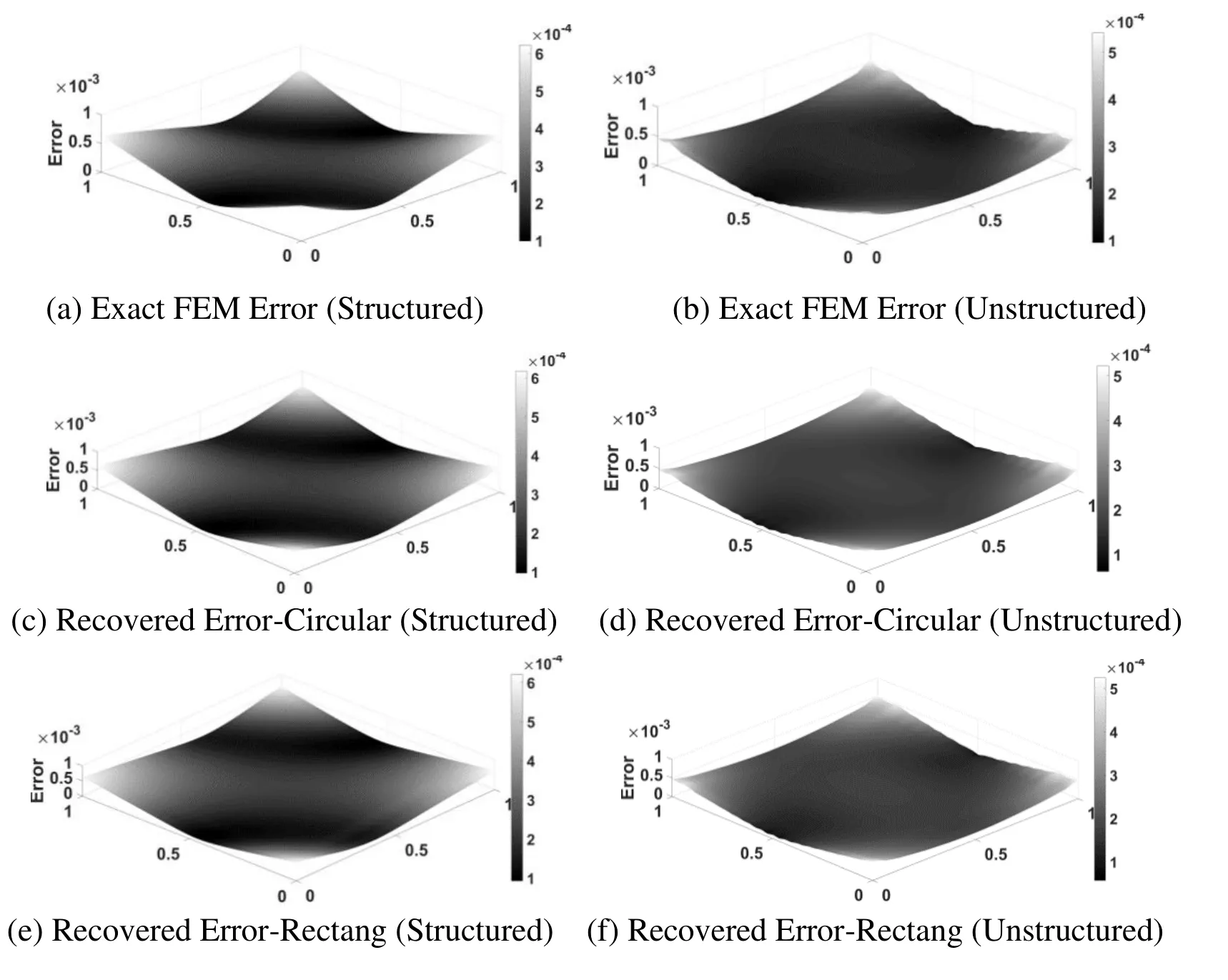
Figure 5:Error distribution in plate problem using different support domain shape in recovery based analysis [linear elements,structured mesh at size =1/32 &unstructured mesh at 1978 elements]

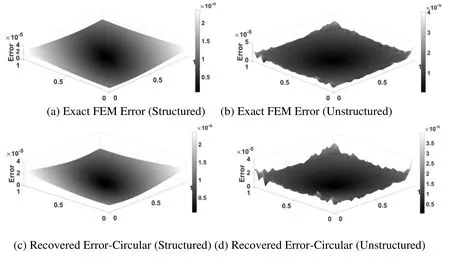
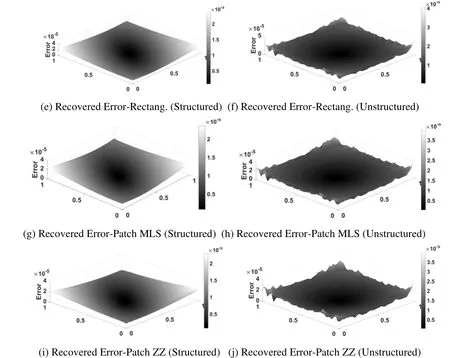
Figure 6:Error distribution in plate problem using different support domain shape in recovery based analysis [quadratic elements,structured mesh at size =1/32 &unstructured mesh at 1978 elements]

Adaptive analysis of the plate problem guided through the error estimation using interpolation based post processing technique for specified accuracy limit is also carried out.Adaptive results are obtained for mesh based patch ZZ recovery,mesh based patch MLS recovery and support domain based MLS recovery technique.Tab.9 and Tab.10 show global errors,the number of element and DOF in refined meshes,obtained from the linear and quadratic elements initial mesh,to bring the accuracy level at target accuracy.The global error in energy norm of higher order element is much lower than global error of lower order elements.The target error of 10% is selected for adaptive finite element analyses employing linear elements discretization and a target error of 1% is fixed for adaptive analyses employing quadratic elements.The computed global error for linear elements is highest for ZZ patch recovery and minimum is for MLS patch recovery technique.For quadratic elements,global error is highest for recovery technique using MLS rectangular support domain.The adaptively refined meshes with target error using least square and MLS interpolation based error estimation are given in Figs.7-10.The initial meshes are adaptively refined to bring the solution error within the prescribed limit.The number of elements required to achieve target accuracy is lesser in MLS interpolation based error estimation as compared to least square based error estimation for linear elements discretization.However,for quadratic element discretization,number of elements required to achieve target accuracy are more in MLS interpolation.It infers that MLS based recovery technique is more efficient than the ZZ recovery technique for linear elements discretization.The refined mesh plots show that the meshes become finer in areas of high local error and become coarser in area of lesser error to get a uniform accuracy throughout the domain.The error distribution patterns and zone of fine mesh in plate domains show good agreement.It concludes that the interpolation techniques based adaptive analysis may predict the high errors zones and control the solution error effectively.

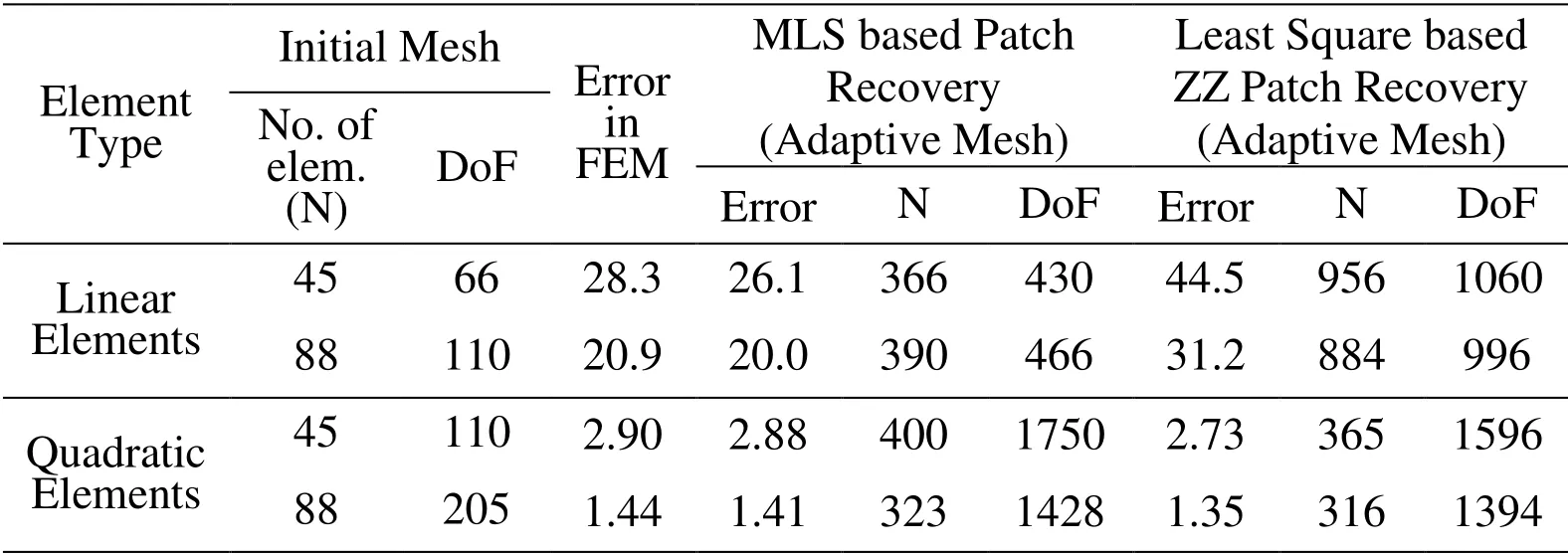
Table 9:Global Errors in Energy Norm and Number of element (N) with DOF of adaptively refined mesh in Recovery Based Adaptive Analysis with different Interpolation types (10% Target Error for linear and 1% Target Error for Quadratic Elements)

Table 10:Global Errors in Energy Norm and Number of element (N) with DOF of adaptively refined mesh in Recovery Based Adaptive Analysis with different support domain (10% Target Error for linear and 1% Target Error for Quadratic Elements)

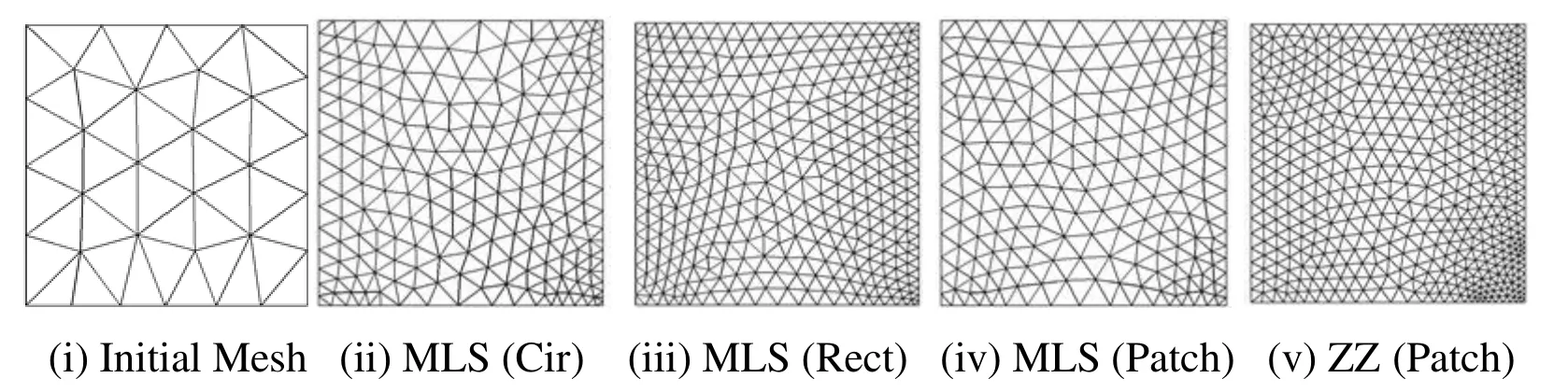
Figure 7:Adaptively refined mesh in Plate Problem Domain using Patch based MLS and ZZ recovery,and Support Domain (SD) based MLS Recovery in Adaptive Analysis [Linear Elements Initial Mesh =45,10% Target Error]

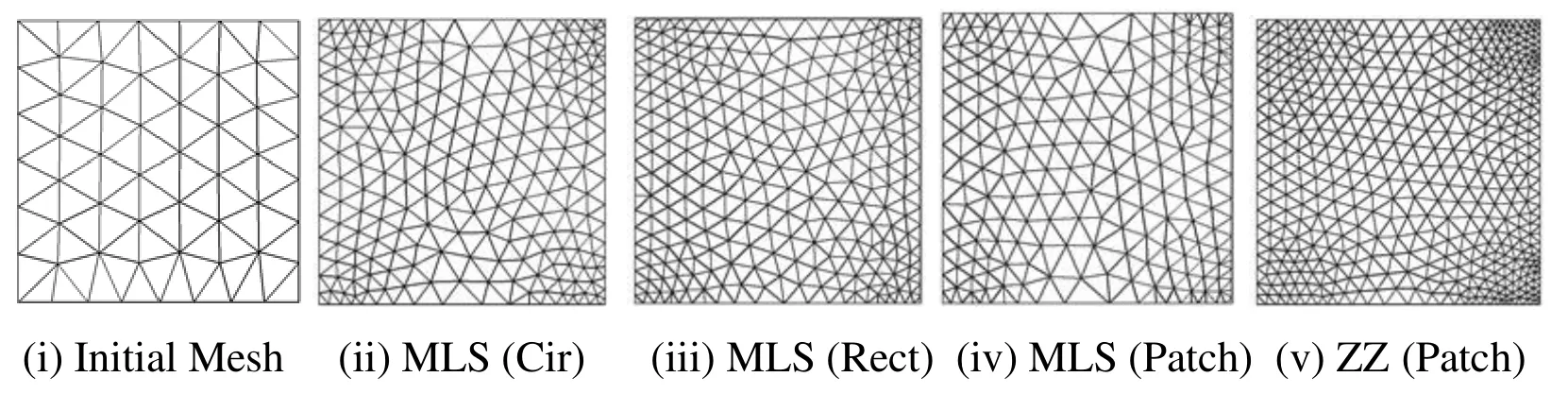
Figure 8:Adaptively refined mesh in Plate Problem Domain using Patch based MLS and ZZ recovery,and Support Domain (SD) based MLS Recovery in Adaptive Analysis [Linear Elements Initial Mesh =88,10% Target Error]

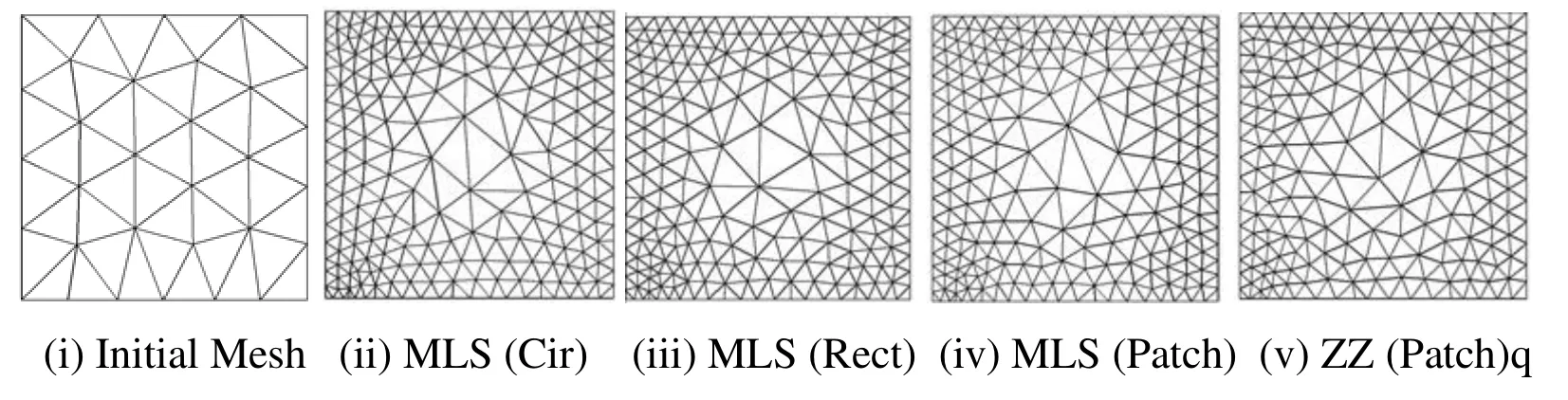
Figure 9:Adaptively refined mesh in Plate Problem Domain using Patch based MLS and ZZ recovery,and Support Domain (SD) based MLS Recovery in Adaptive Analysis [Quadratic Elements Initial Mesh =45,1% Target Error]

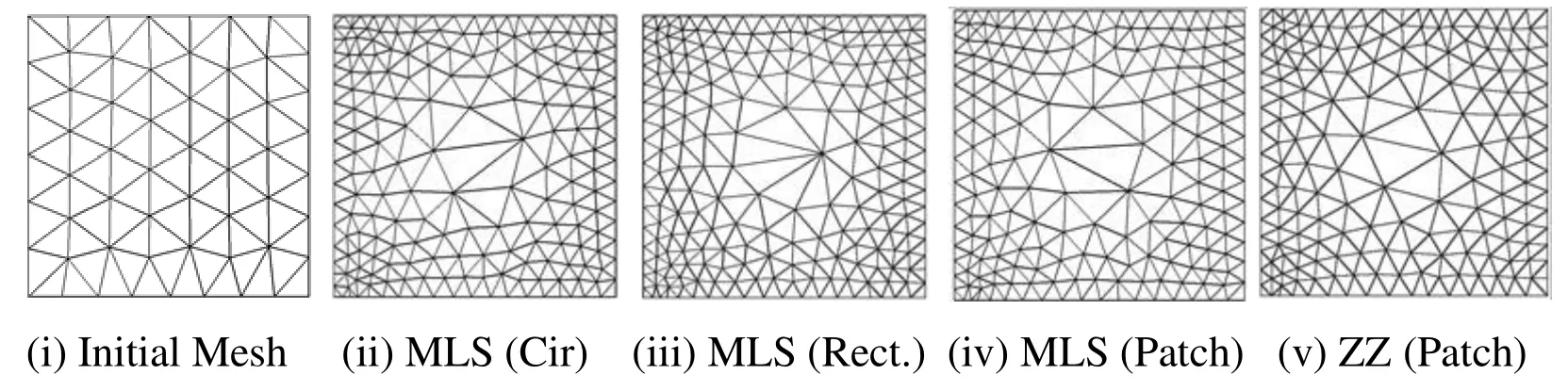
Figure 10:Adaptively refined mesh in Plate Problem Domain using Patch based MLS and ZZ recovery,and Support Domain (SD) based MLS Recovery in Adaptive Analysis [Quadratic Elements Initial Mesh =88,1% Target Error]

5.1.2 Recovery parameter:dilation parameter of MLS interpolation technique

The dilation parameter regulates the density of the particle distribution in support domain.The suitable dilation parameter supports the MLS interpolation function to automatically satisfy its completeness condition.The dilation parameters values with linear element meshing considered in the study are 2.5,3.0 and 4.0.For quadratic element meshing,the dilation parameters values are 4.5,5.5 and 6.5.The convergence rate of error and effectivity of error estimation with different dilation parameter values with increasing fineness order of mesh in MLS interpolation based post-processed finite element analysis are given in Tab.5 and Tab.6.The tables show that the order of error in energy norm increases with the increase of dilation parameter and effectivity of error estimation decreases with increase of the dilation parameter and,the rate of convergence is not significantly affected by the higher value of dilation parameter in case linear element meshing.For higher order element,the order of error decreases and convergence rates increase with increase of dilation parameter and the finite element analysis with quadratic element shows improved performance under different dilation parameters.However,it is observed that there will be a particular value of dilation parameter to provide an optimal performance.The local (element) effectivity frequency using linear and quadratic elements for dilation parameter is plotted in Fig.5 at last refinement level considered,to study the effect on recovery of finite element solution.The figure depicts that the errors using linear elements is not much affected by increasing the dilation parameter value as the number of element effectivity with value about one,is more or less same with different dilation parameter.However,number of elements of effectivity with values nearly to one are shown to increase in analysis using quadratic elements mesh.

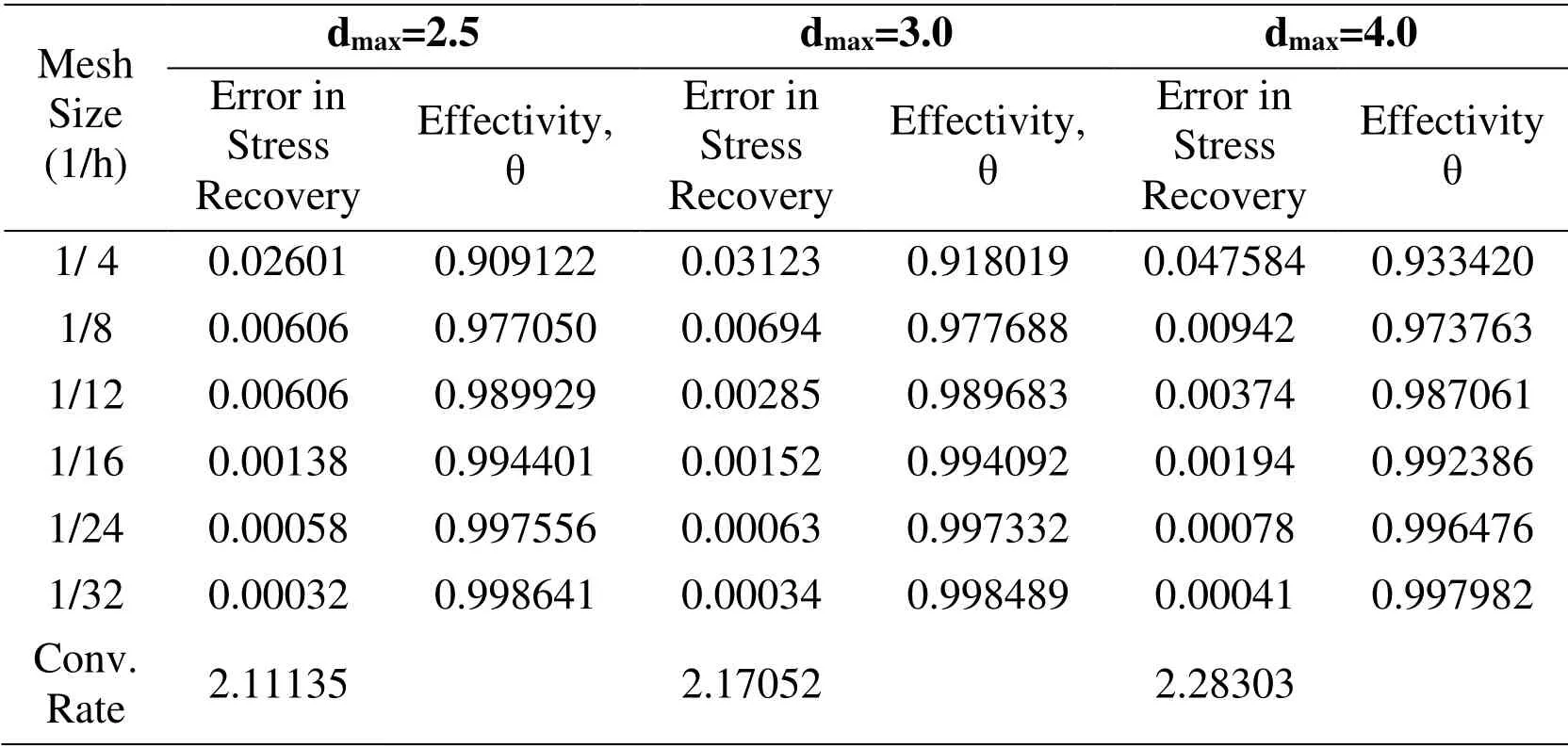
Table 11:Predicted Errors and Global Effectivity for Square Plate problem with Dilation parameter (dmax) in Post-processing Techniques (Linear Elements)

Table 12:Predicted Errors and Global Effectivity for Square Plate problem with Dilation parameter (dmax) in Post-processing Techniques (Quadratic Elements)

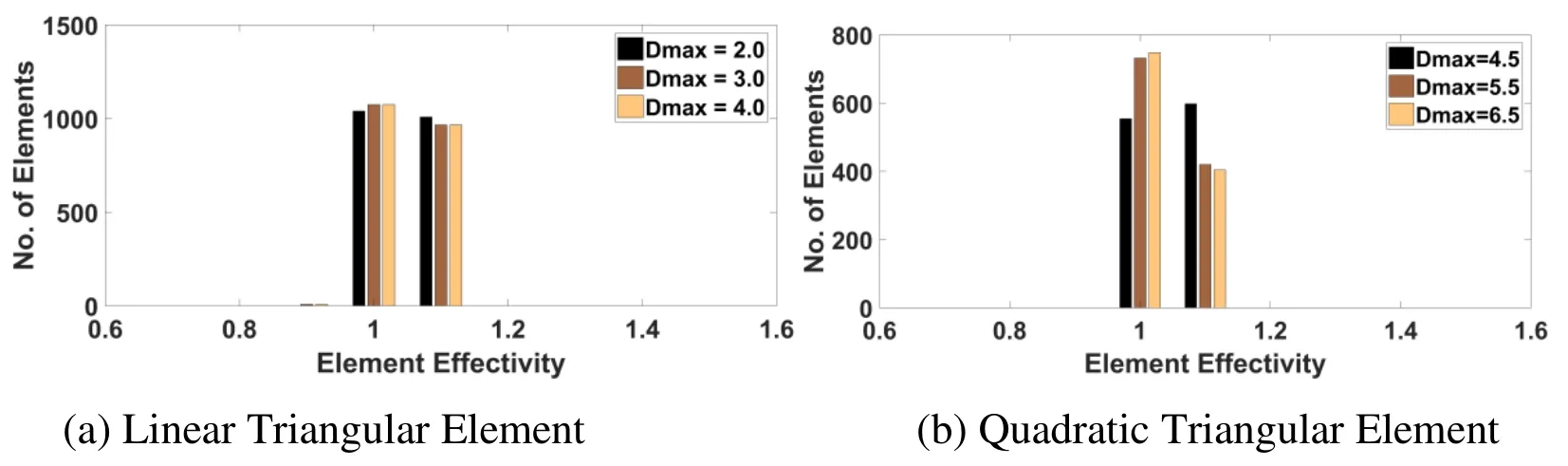
Figure 11:Histogram-Element Effectivity vs. Number of Elements for plate problem using different dilation parameters in Recovery based Finite Element Analysis

5.1.3 Recovery parameter:number of basis function terms

In the post-processing technique,field variable or its derivative is assumed to belong to polynomial expansion of the same complete order or higher order polynomial as that present in the basis function.According to so-called ZZ super-convergent patch recovery technique [Zienkiewicz and Zhu (1992)],the nodal values of stress belongs to a polynomial expansion of the same complete order as that present in the basis function.According to Ahmed and Singh [Ahmed and Singh (2008)] for element patch,the nodal values of field variables belong to a higher order polynomial expansion.For order of polynomial expansion in the basis function effect study,two set of number of basis function terms namely,3,6,9 and 6,9,10 are used,for fitting the derivatives of field variable over the mesh independent node patches (support domain),for linear and quadratic elements respectively.The convergence rate of error and effectivity of error estimation with set of number of basis function terms at different element fineness in MLS interpolation based post-processed finite element analysis are given in Tab.7 and Tab.8.From the tables,it can be concluded that moving least square based postprocessed analysis,for the field variable derivative interpolation requires polynomial expansion of the one order higher as that present in the basis function.The local (element) effectivity frequency using linear and quadratic elements for various number of basis function terms is shown in Fig.6 at last refinement level considered.The figure depicts that performance of recovery based finite element analysis will not improve by taking higher number of basis function terms for lower order elements as the number of element of effectivity with value nearly one are not significantly increased by using more number of basis function terms.

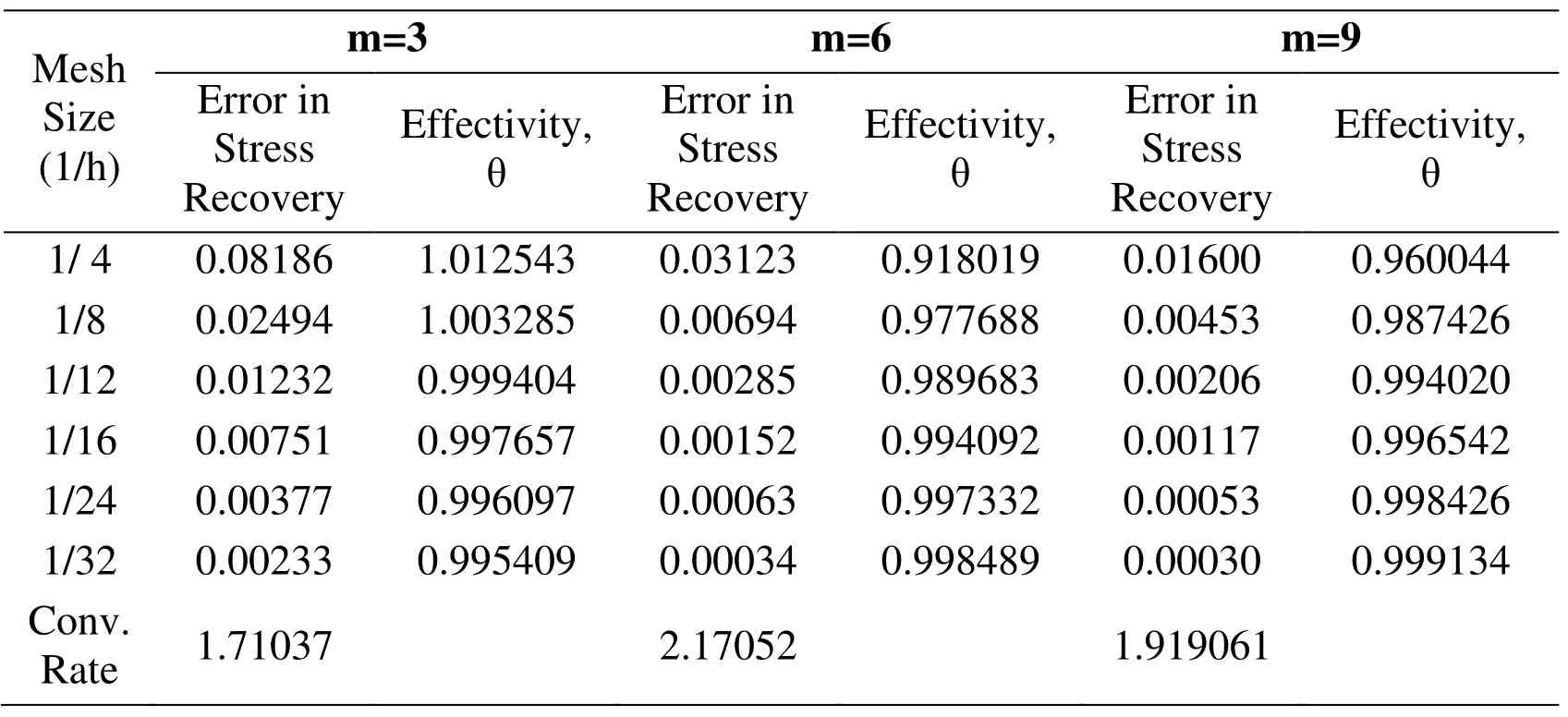
Table 13:Predicted Errors and Global Effectivity for Square Plate problem with number of basis function terms (m) in Post-processing Techniques (Linear Triangular Meshing)

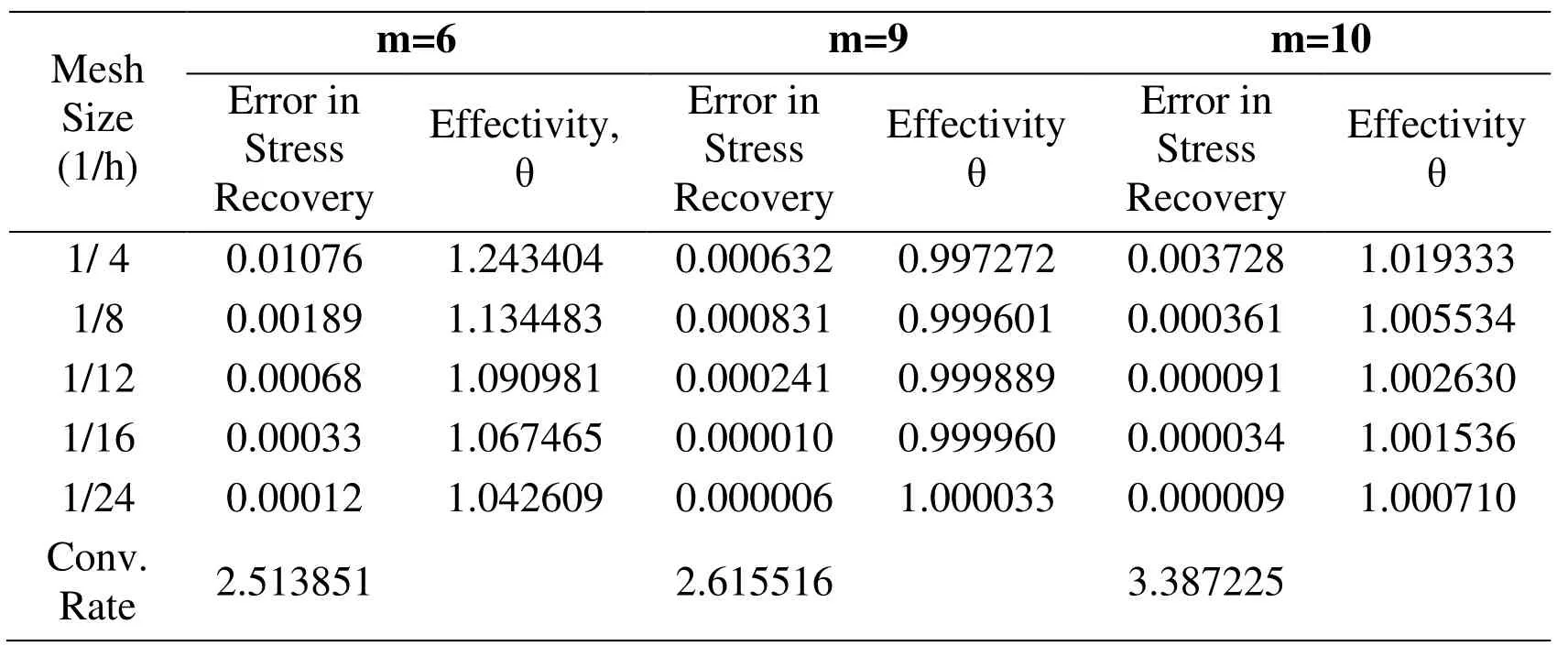
Table 14:Predicted Errors and Global Effectivity for Square Plate problem with number of basis function terms (m) in Post-processing Techniques (Quadratic Triangular Meshing)

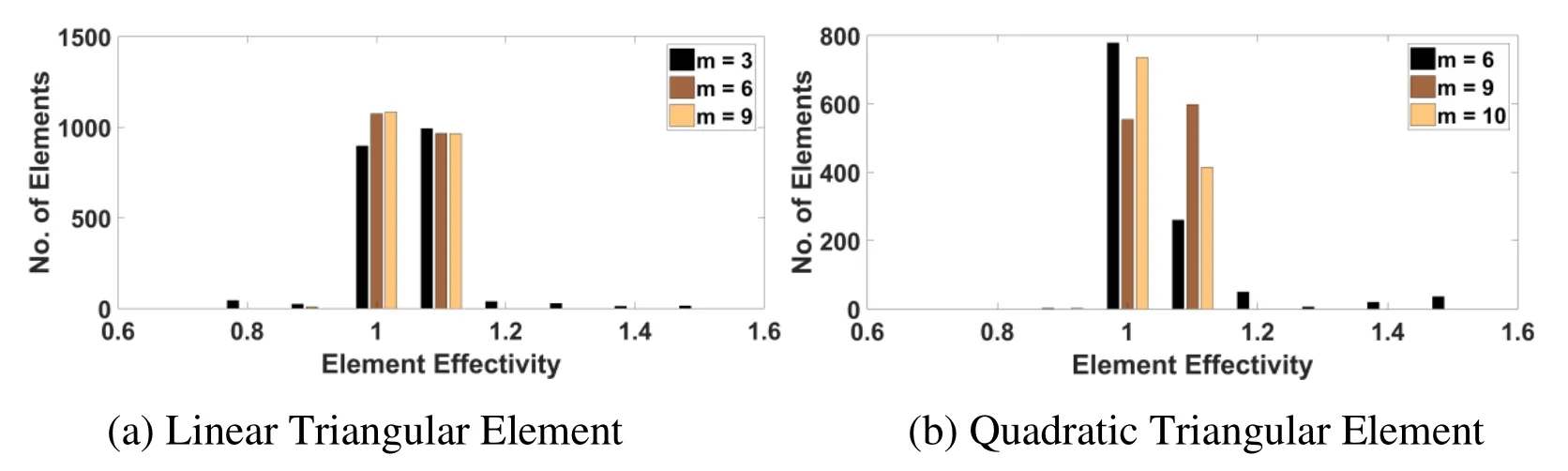
Figure 12:Histogram-Element Effectivity vs. Number of Elements for plate problem using different order of basis function in Recovery based Finite Element Analysis

5.2 Elastic plate problem with central hole

The elastic square plate with central circular opening,a typical stress concentration problem,is also selected for error recovery quality study of interpolation based recovery method under different interpolations and patches construction type.The side of the square plate is 5 unit with hole radius of one unit.The normal and vertical displacement components are zero along the circular arc boundary.The normal displacement component and shear stress are zero over the line of symmetry.Static boundary conditions are imposed from the given traction equations.The plate stress field are given in Eqs.(5) to (7) [Zienkiewicz and Zhu (1992)].The discretized domain for plate problem with circular opening is shown in Fig.13 (one quarter due to symmetry).

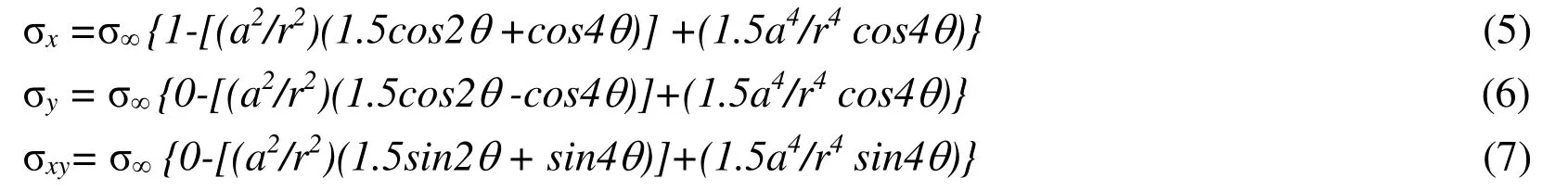
wherer= y2 + x2and σ∞is the uniaxial traction applied at infinity.

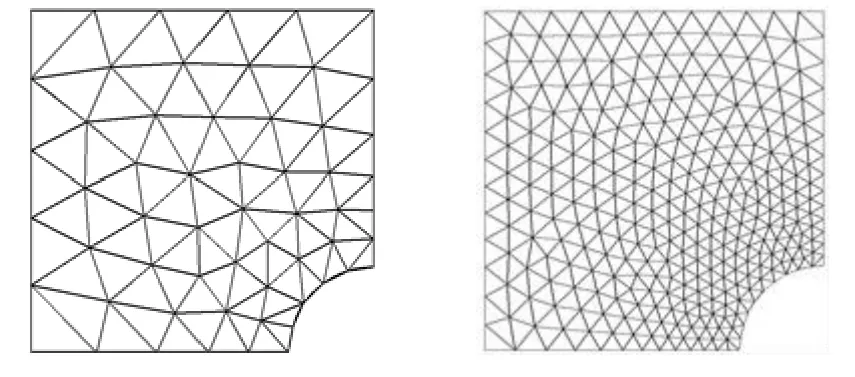
Figure 13:Central hole plate discretized with triangular elements

5.2.1 Recovery parameter:interpolation technique and patch construction

The recovery parametric study of interpolation based recovery method for the interpolation technique and patch construction considers dilation parameter value as 3.5 for linear elements and 4.0 for quadratic elements.The number of terms in polynomial basis is taken as 6 and 9 respectively for linear and quadratic elements.The quality of error estimation of the recovery analysis using least square and moving least square techniques,linear and quadratic element meshing to form circular and rectangular support domain error are presented in terms of convergence and effectivity in Tab.15-Tab.18.The tables show that least square interpolation method give better quality of error estimation as compared to MLS interpolation method for plate problem with central opening.The lower order elements perform better as compared to higher order element for analysed stress concentration problem with post-processed based finite element analysis using interpolation based recovery techniques.The rectangular support domain has better performance as compared to circular shape of support domain in MLS interpolation based recovery analysis.The order of error in energy norm obtained is higher in rectangular support domain as compared to the other patch construction type used in interpolation based recovery analysis.

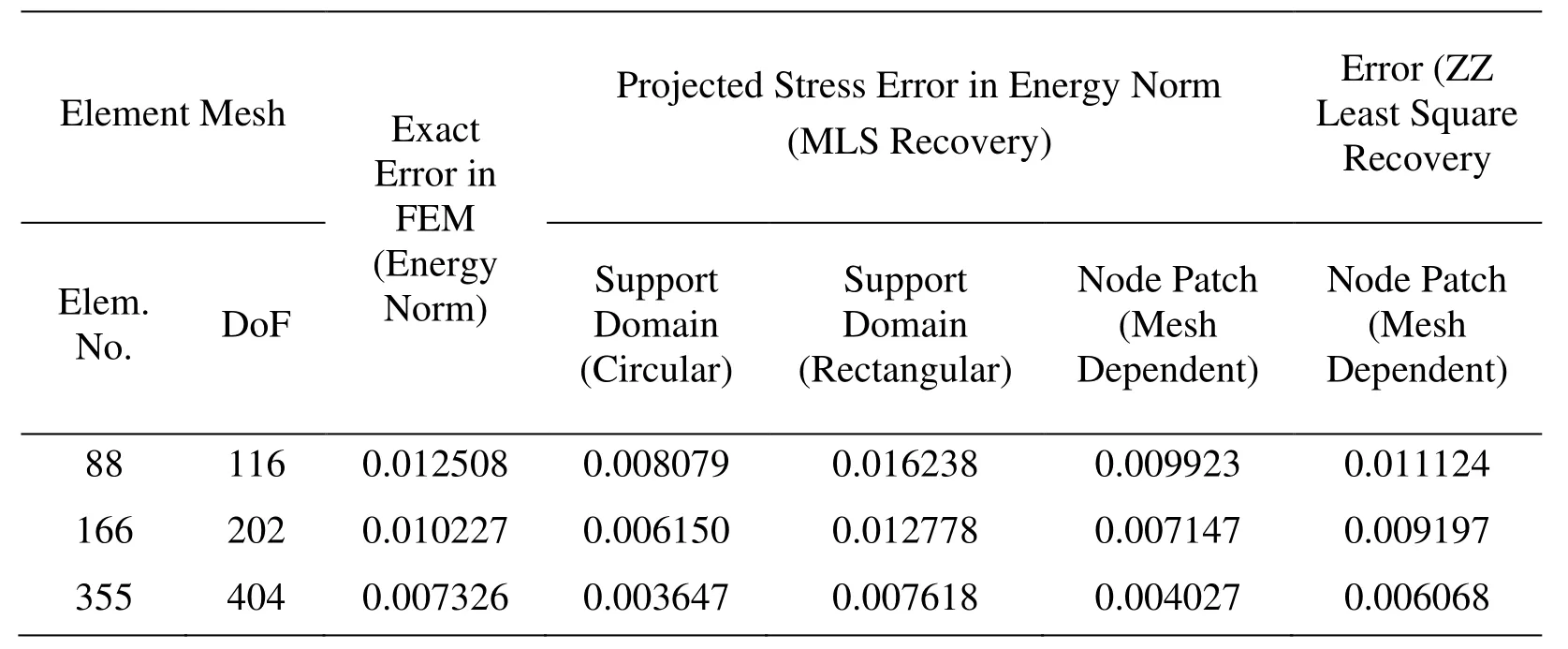
Table 15:Predicted Errors for Central Hole Plate with Interpolation Type and patch construction in Post-processing Techniques (Linear Elements)

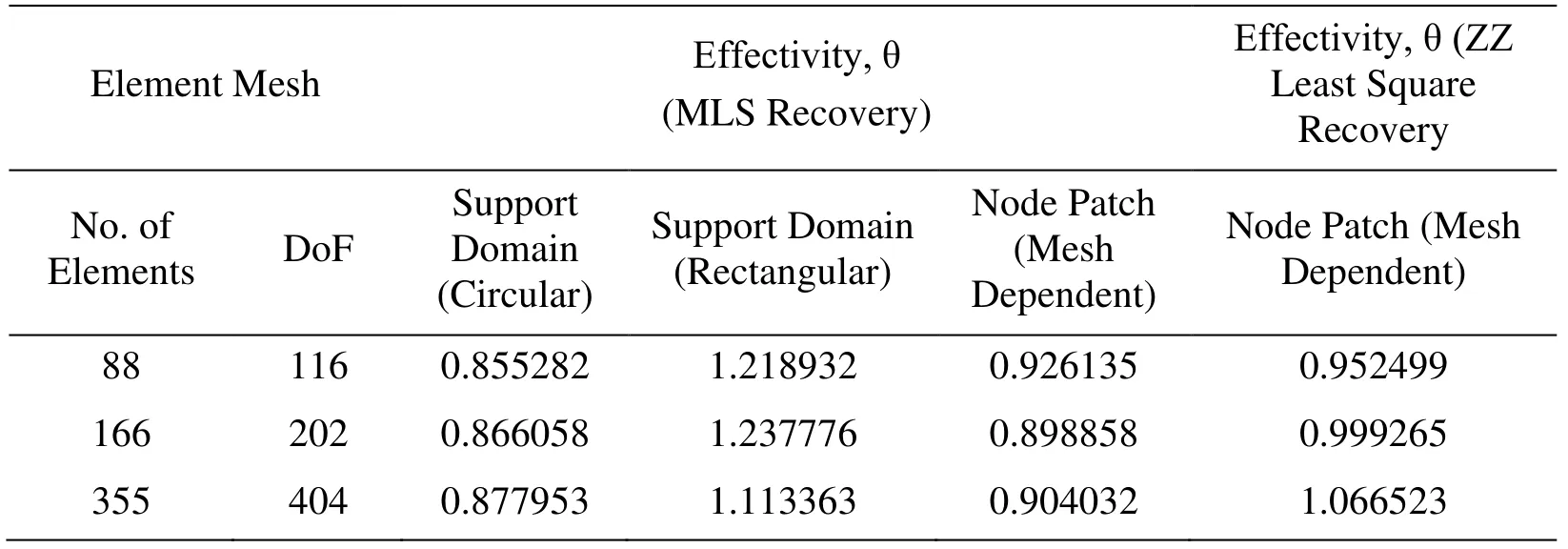
Table 16:Global Effectivity for Central Hole Plate with Interpolation Type and patch construction in Post-processing Techniques (Linear Elements)

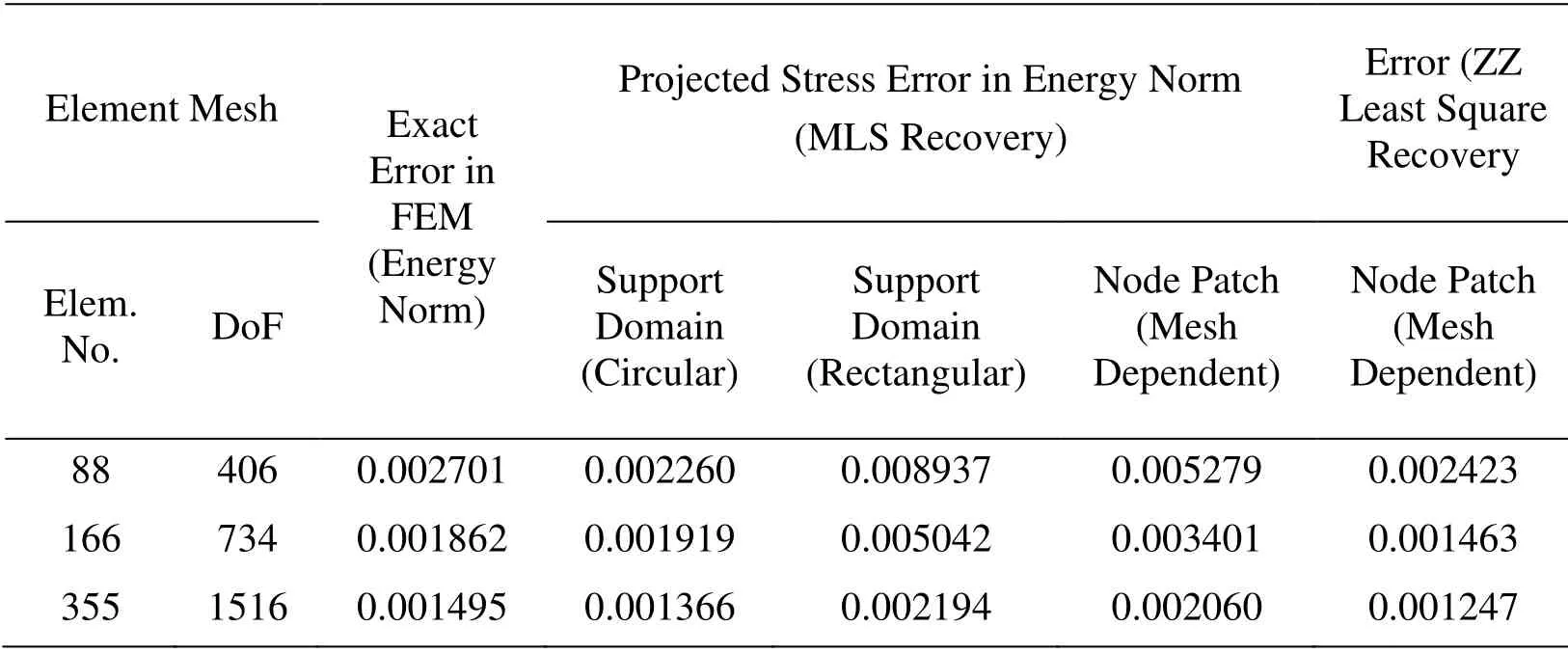
Table 17:Predicted Errors for Central Hole Plate with Interpolation Type and patch construction in Post-processing Techniques (Quadratic Elements)

Table 18:Global Effectivity for Central Hole Plate with Interpolation Type and patch construction in Post-processing Techniques (Quadratic Elements)

Table 19:Exact and projected Global Errors in Energy Norm for Central Hole Plate using least square (ZZ) Patch,MLS Patch Recovery and MLS Support Domain Recovery

Tab.19 shows global errors obtained with least square interpolation recovery (ZZ) and moving least square interpolation recovery considering node patches and support domains for central hole plate problem finite element analysis using the linear and quadratic elements.The computed global error for linear elements is highest for ZZ patch recovery and minimum is for MLS patch recovery technique.For quadratic elements,global error is highest for recovery technique using MLS rectangular support domain similar to the global error obtained for plate problem without hole.

6 Conclusions

The study presents discretization errors estimation under varying parameters of finite element error recovery techniques.The quality of error estimation of finite element numerical experiments,using the interpolation based recovery technique parameters,on elastic plate problems is investigated in terms of global and local effectivity,rate of error convergence and adaptively refined mesh at specified error.The linear and quadratic triangular elements have been used for the discretization of the problem domain.The effect on the performance of interpolation based recovery technique is studied by considering four recovery parameters namely,type of interpolation technique and patch construction for interpolation,dilation parameter and number of terms in basis function.The study considers two interpolation technique namely,least square (ZZ recovery) and moving least square interpolation techniques employing mesh reliant as well as mesh free patches (support domains).The main conclusions of the study are summarized below.

1.The basic recovery parameters of interpolation based recovery technique have pronounced effect on the finite element analysis post processed results.

2.The finite element analysis (FEA) employing the error recovery procedures provides much lower order of errors as compared to FEA solution errors and error convergence is also much higher than the convergence of FEA solution errors with increasing order of meshing.

3.The moving least square interpolation based recovery technique is suitable to enhance the quality of error estimation for linear element discretization while for the higher order elements,least square (ZZ recovery) technique may be used for enhanced performance.

4.The quality of error estimation of mesh free patches (support domains) used interpolation based recovery technique is superior to mesh dependent patches based error estimation.

5.The rectangular support domain construction has better convergence performance as compared to circular shape of support domain for both lower and higher element mesh in mesh free recovery based finite element analysis.The convergence rate achieved is about two orders higher in case of rectangular support domain.

6.The computational analysis results obtained for error estimation quality vary with the variation of dilation parameters.A suitable value of the dilation parameter will provide optimal performance for the problem.

7.The improved quality of error estimation in moving least square based post-processed analysis is obtained when the field variable derivative is considered belong to a higher order polynomial expansion as that present in the basis function.8 The error distribution patterns and zone of fine mesh in problem domain show good agreement and the interpolation techniques based adaptive analysis may be utilize to predict the high errors zones and control the solution error effectively.

Conflict of interest:The author(s) declare(s) that there is no conflict of interest regarding the publication of this paper.

Acknowledgement:The author acknowledges the Deanship of Scientific Research for proving administrative and financial supports.Funding for this work has been provided by the Deanship of Scientific Research,King Khalid University,Ministry of Education,Kingdom of Saudi Arabia under research grant award number R.G.P.1/82/40 (1440).The authors also acknowledge to the Dean,College of Engineering for his valuable support and help.

References

Ahmed,M.;Singh,D.(2008):An adaptive parametric study on mesh refinement during adaptive finite element simulation of sheet forming operations.Turkish Journal of Engineering and Environmental Sciences,vol.13,pp.1-13.

Ahmed,M.;Singh,D.;Desmukh,M.N.(2018):Interpolation type stress recovery technique based error estimator for elasticity problems.Mechanika,vol.24,no.5,pp.672-679.

Ainsworth,M.;Oden,J.T.(1997):A posteriori error estimation in finite element analysis.Computational Methods in Applied Mechanics and Engineering,vol.142,pp.1-88.

Aragón,A.M.;Simone,A.(2017):The discontinuity-enriched finite element method.International Journal for Numerical Methods in Engineering,vol.12,pp.1589-1613.

Bathe,K.J.;Zhang,L.(2017):The finite element method with overlapping elements-A new paradigm for CAD driven simulations.Computer and Structures,vol.182,pp.526-539.

Blacker,T.;Belytschko,T.(1994):Superconvergent patch recovery with equilibrium and conjoint interpolant enhancements.International Journal for Numerical Methods in Engineering,vol.37,pp.517-536.

Bramble,J.H.;Schatz,A.H.(1977):Higher order local accuracy by averaging in finite element method.Mathematics of Computation,vol.31,pp.94-111.

Dow,J.O.(1999):A Uniform Approach to the Finite Element Method and Error Analysis Procedures.Academic Press,London.

Gratsch,T.;Bathe,K.(2005):A Posteriori error estimation techniques in practical finite element analysis.Computers &Structures,vol.83,pp.235-265.

Hinton,E.;Campbell,J.S.(1974):Local and global smoothing of discontinuous finite element functions using a least square methods.International Journal for Numerical Methods in Engineering,vol.8,pp.61-80.

Wang,J.G.;Liu,G.R.(2002):On the optimal shape parameters of radial basis functions used for 2-D meshless methods.Computational Methods in Applied Mechanics and Engineering,vol.191,no.23-24,pp.2611-2630.

Kim,K.Y.;Lee,H.C.(2010):A posteriori error estimators for nonconforming finite element methods of the linear elasticity problem.Journal of Computational and Applied Mathematics,vol.235,pp.186-202.

Kanber,B.;Bozkurt,O.Y.;Erklig,A.(2013):Investigation of RPIM shape parameter effects on the solution accuracy of 2D elastoplastic problems.International Journal for Computational Methods in Engineering Science and Mechanics,vol.14,pp.354-366.

Li,X.D.;Wiberg,N.E.(1994):An posteriori error estimate by element patch postprocessing,adaptive analysis in energy and L2norms.Computers and Structures,vol.53,pp.907-919.

Liu,Y.C.;Elmaraghy,H.A.(1992):Assesment of discretized errors and adaptive refinement with quadrilateral finite element.International Journal for Numerical Methods in Engineering,vol.33,pp.781-798.

Liu,G.R.;Nguyen-Thoia,T.;Lam,K.Y.(2008):A novel alpha finite element method (αFEM) for exact solution to mechanics problems using triangular and tetrahedral elements.Computational Methods in Applied Mechanics and Engineering,vol.197,pp.3883-3897.

Mucki,R.;Whiteman,J.R.(1995):A posteriori error estimates and adaptivity for finite element solutions in finite elasticity.International Journal for Numerical Methods in Engineering,vol.38,pp.775-795.

Mirzaei,D.(2015):Analysis of moving least squares approximation revisited,Journal of Computational and Applied Mathematics,vol.282,pp.237-250.

Nie Y.F.;Atluri,S.N.;Zuo,C.W.(2006):The optimal radius of the support of radial weights used in moving least squares approximation.Computer Modeling in Engineering &Sciences,vol.12,no.2,pp.137-147.

Onate,E.;Perazzo,F.;Miquel,J.(2001):A finite point method for elasticity problems.Computers and Structures,vol.79,pp.2151-2163.

Parret-Fréaud,A.;Rey,V.;Gosselet,P.;Rey,C.(2016):Improved recovery of admissible stress in domain decomposition methods-application to heterogeneous structures and new error bounds for FETI-DP.International Journal for Numerical Methods in Engineering,vol.111,no.1,pp.69-87.

Perko,J.;Šarler,B.(2007):Weight function shape parameter optimization in meshless methods for non-uniform grids.Computer Modeling in Engineering and Sciences,vol.19,no.1,pp.55-68.

Rajendran,S.;Liew,K.M.(2003):Optimal stress sampling points of plane triangular elements for patch recovery of nodal stresses.International Journal for Numerical Methods in Engineering,vol.58,pp.579-607.

Sharma,R.;Zhang,J.;Langelaar,M.;van Keulen,F.;Aragón A.M.(2018):An improved stress recovery technique for low-order 3D finite elements.International Journal for Numerical Methods in Engineering,vol.114,pp.88-103.

Ubertini,F.(2004):Patch recovery based on complementary energy.International Journal for Numerical Methods in Engineering,vol.59,no.11,pp.1501-1538.

Ullah,Z.;Coombs,W.M.;Augarde,C.E.(2013):An adaptive finite element/meshless coupled method based on local maximum entropy shape functions for linear and nonlinear problems.International Journal for Numerical Methods in Engineering,vol.267,pp.111-132.

Xing,H.L.;Wang,S.;Makinouchi,A.(1999):An adaptive mesh h-refinement algorithm for finite-element modelling of sheet forming.Journal of Materials Processing Technology,vol.91,pp.183-190.

Zhu,J.Z.;Zienkiewicz,O.C.(1988):Adaptive techniques in the finite element method.Computational Methods in Applied Mechanics and Engineering,vol.4,pp.197-204.

Zienkiewicz,O.C.;Zhu,J.Z.(1987):A simple error estimator and adaptive procedure for practical engineering analysis.International Journal for Numerical Methods in Engineering,vol.24,pp.333-357.

Zienkiewicz,O.C.;Zhu,J.Z.(1992):The superconvergent patch recovery and a posteriori error estimates.Part I,the error recovery technique.International Journal for Numerical Methods in Engineering,vol.33,pp.1331-1364.

Zienkiewicz,O.C.;Zhu,J.Z.(1992):The superconvergent patch recovery and a posteriori error estimetes.Part II:error estimates and adaptivity.International Journal for Numerical Methods in Engineering,vol.33,pp.1365-1382.

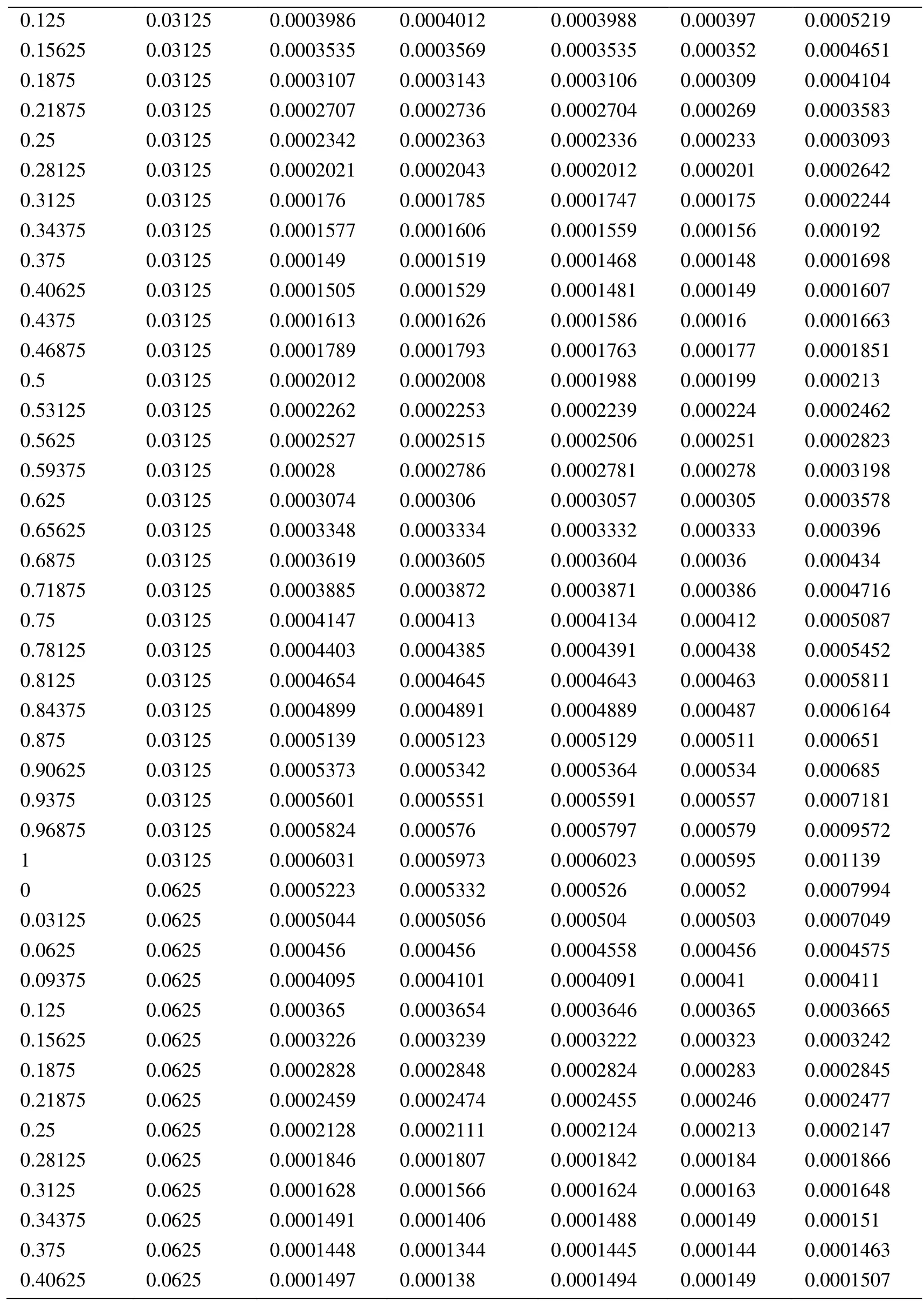
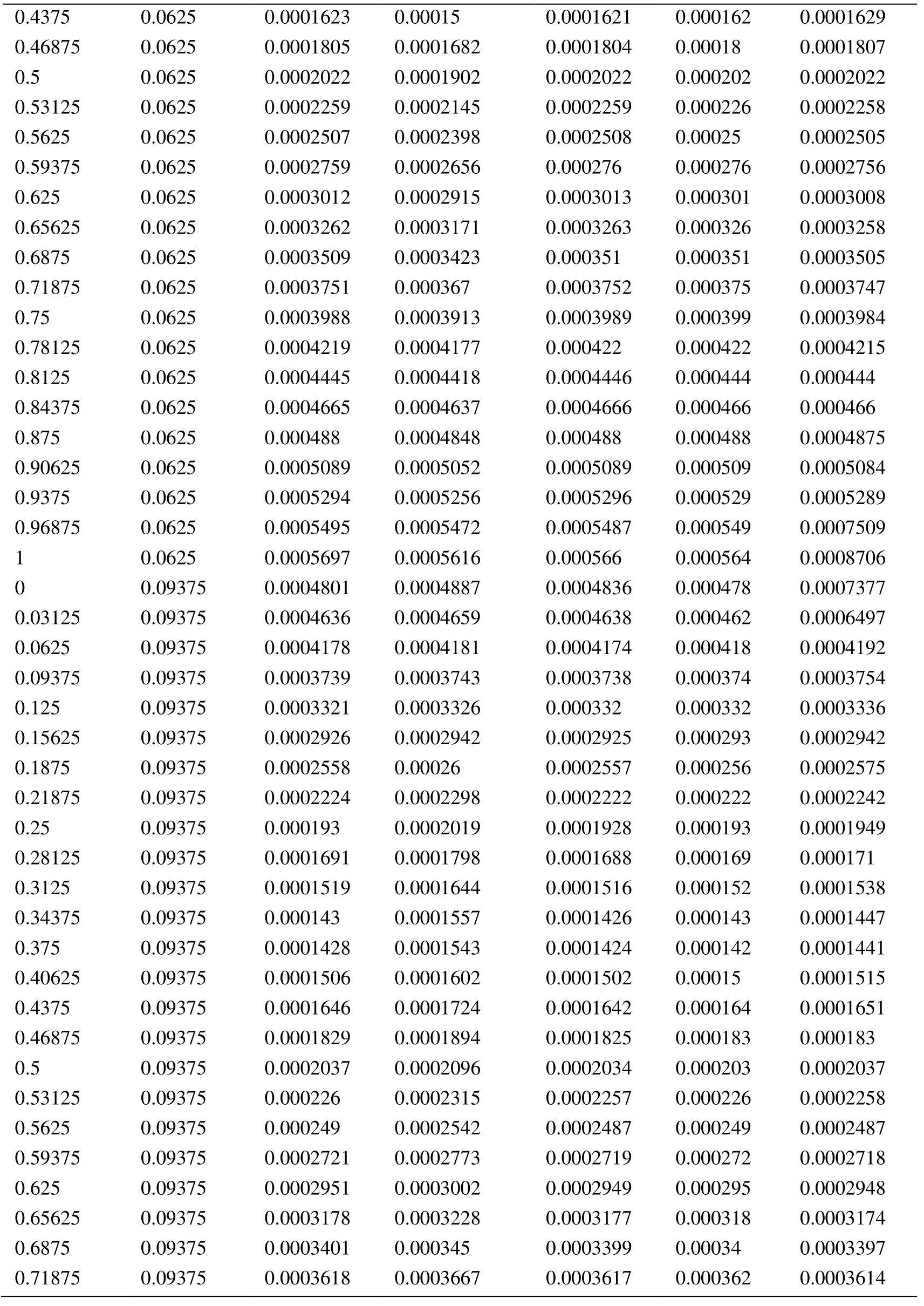
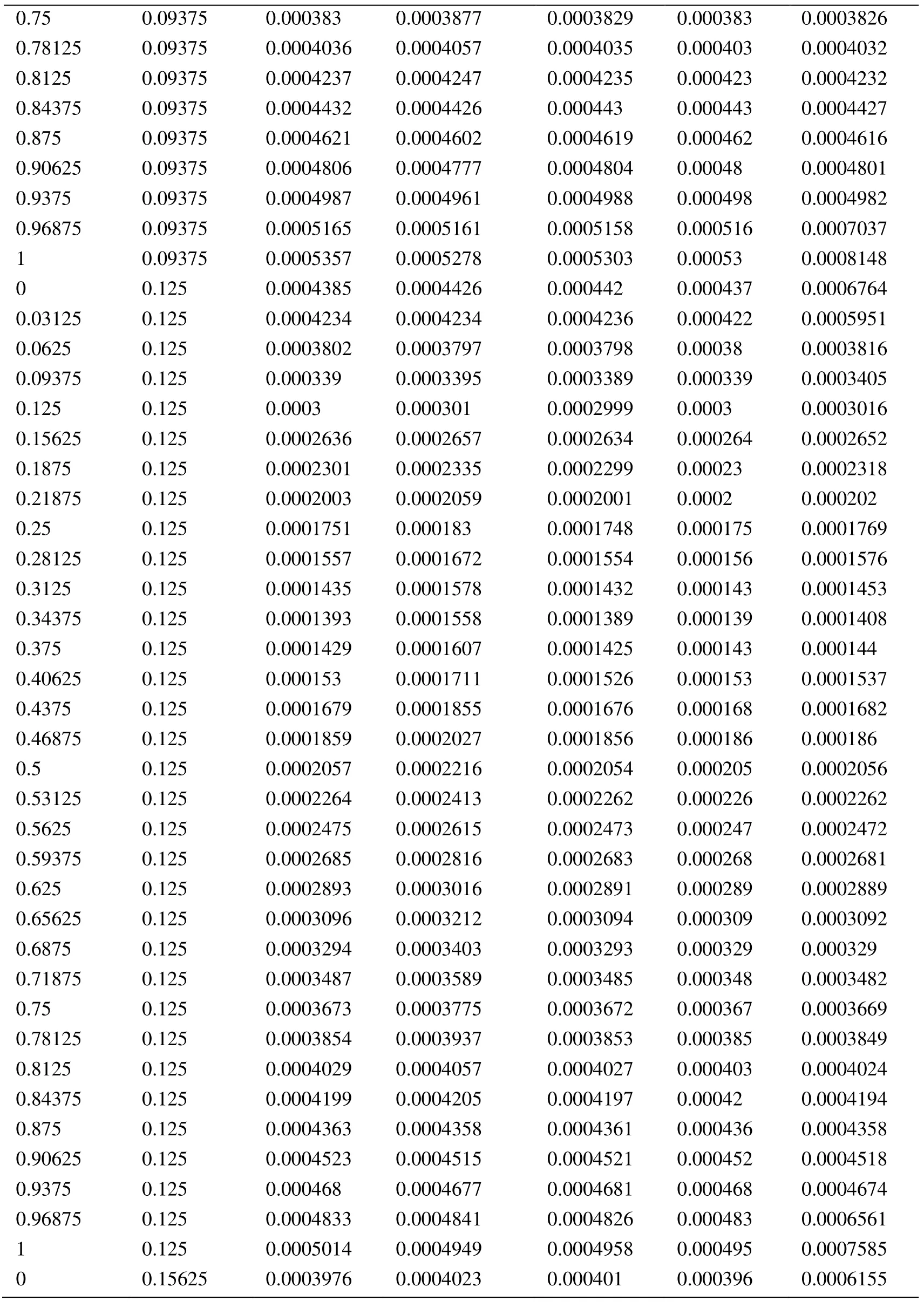
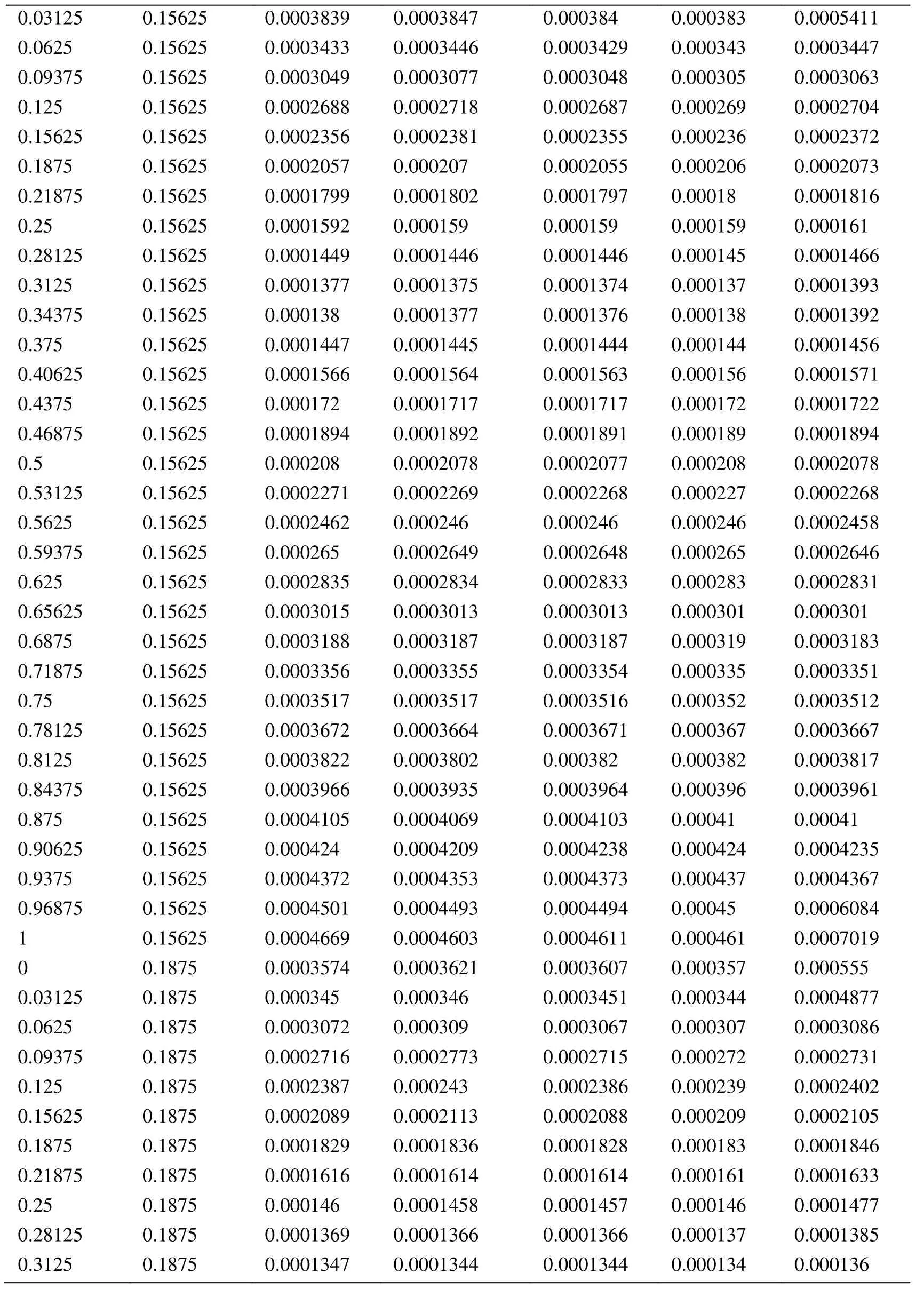
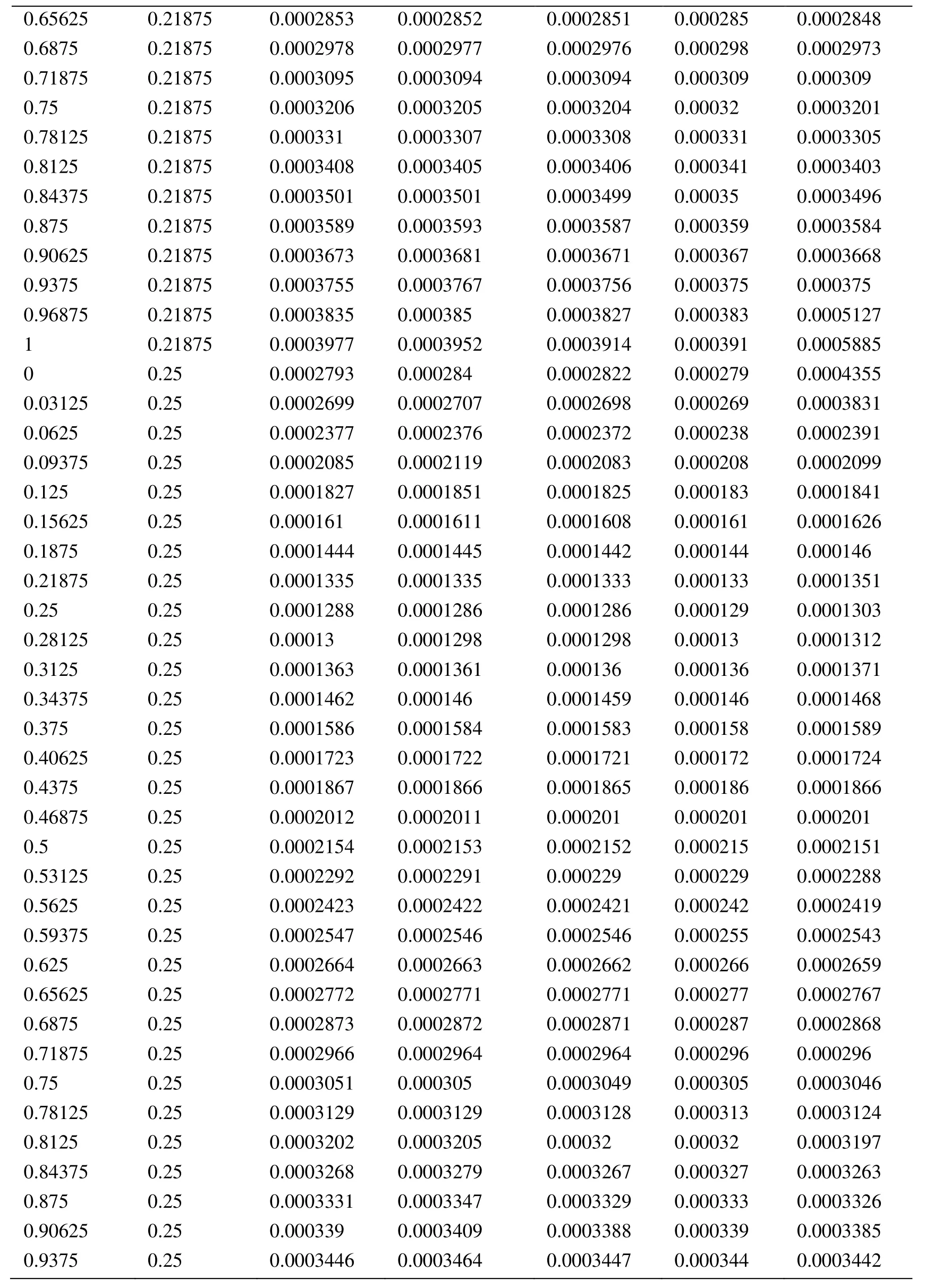
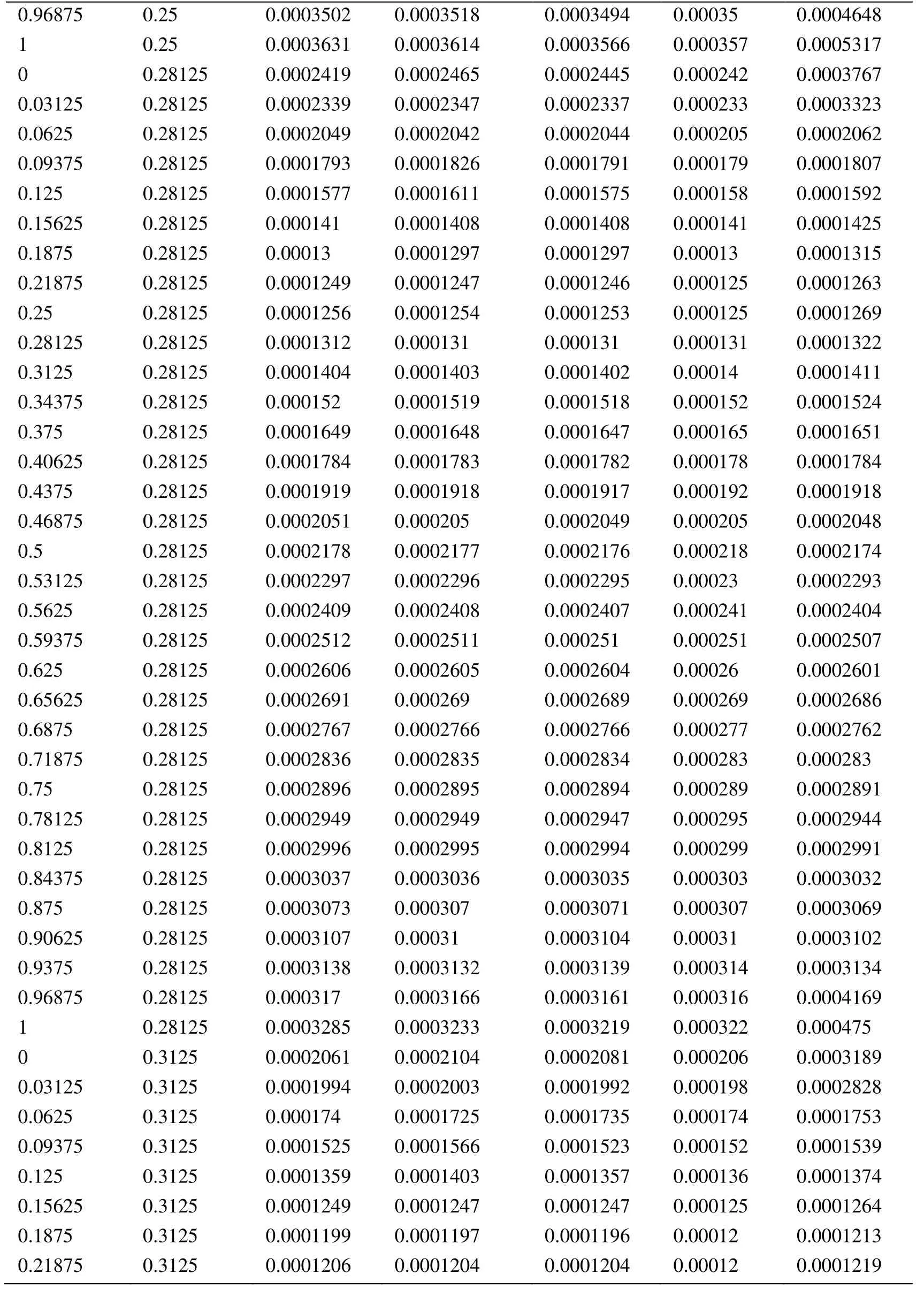
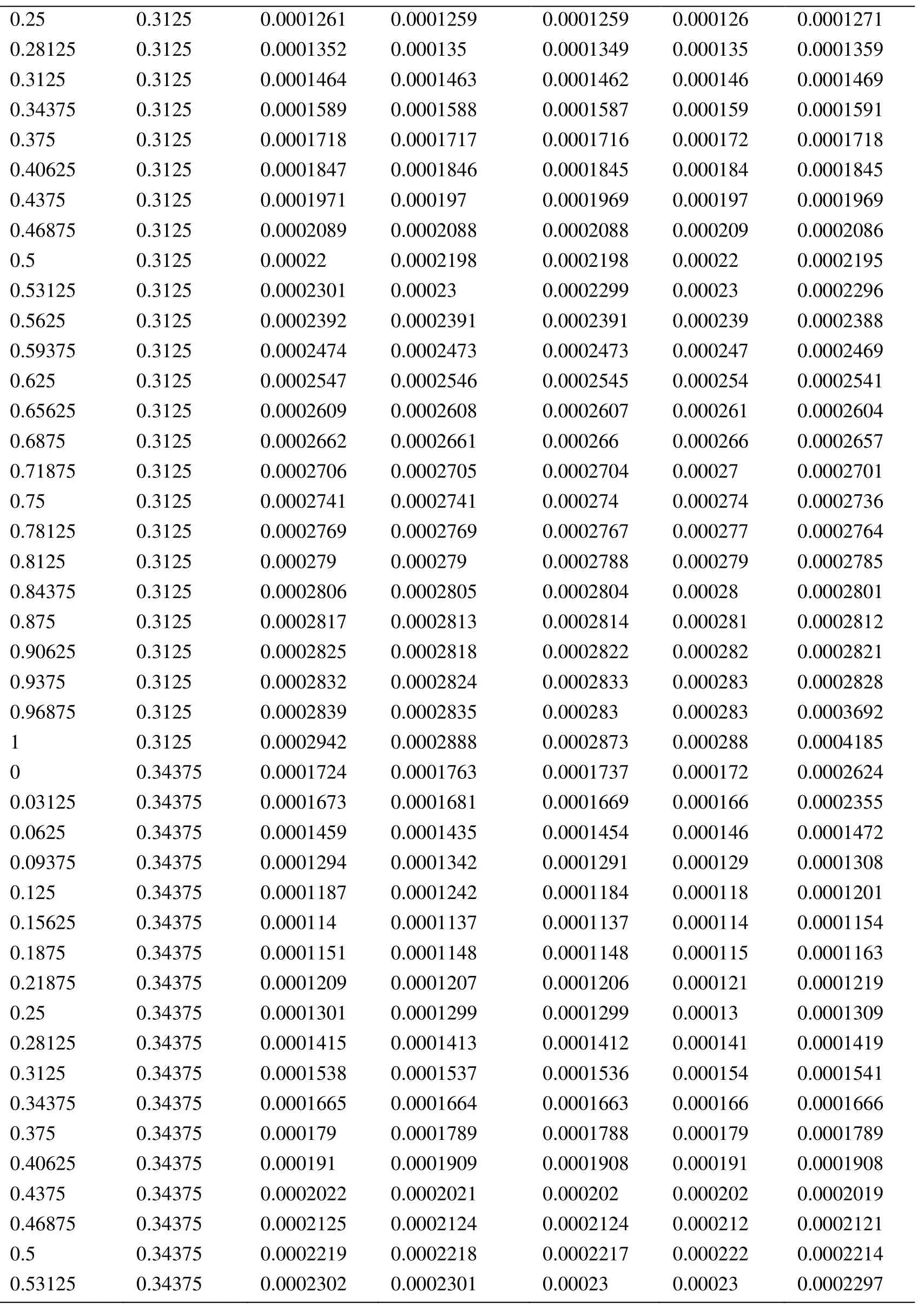
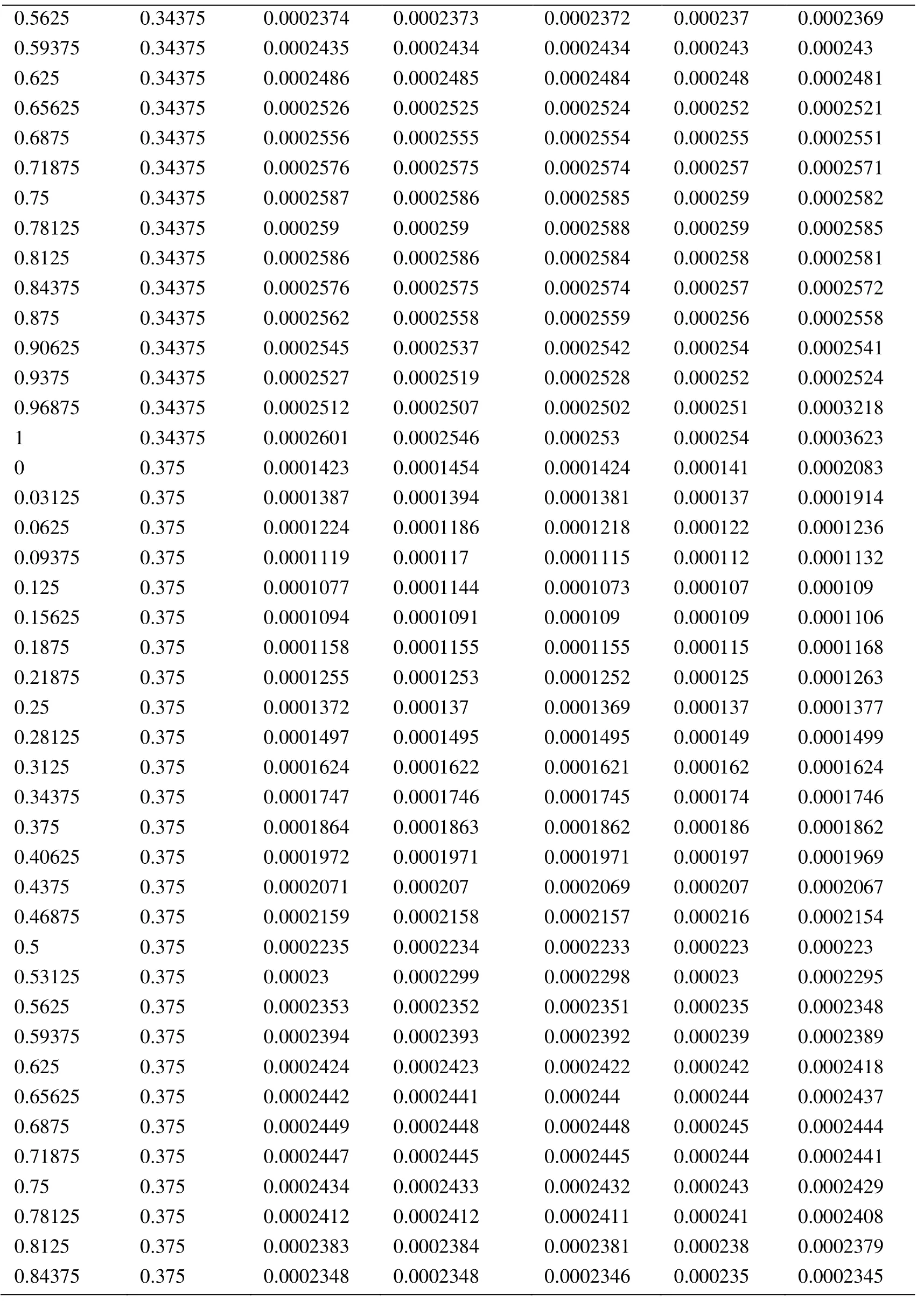
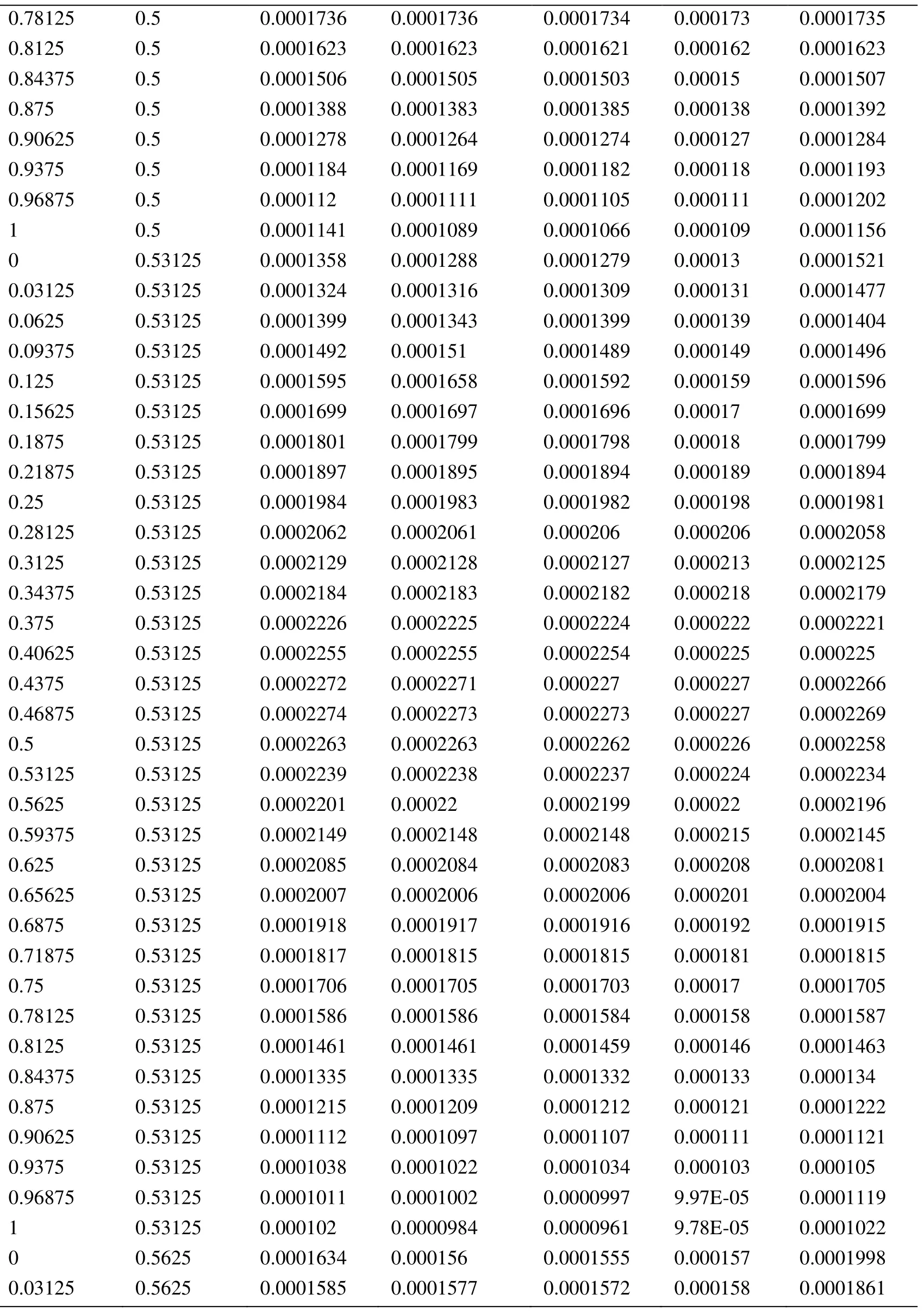
Appendix A.Exact Error and Projected Error

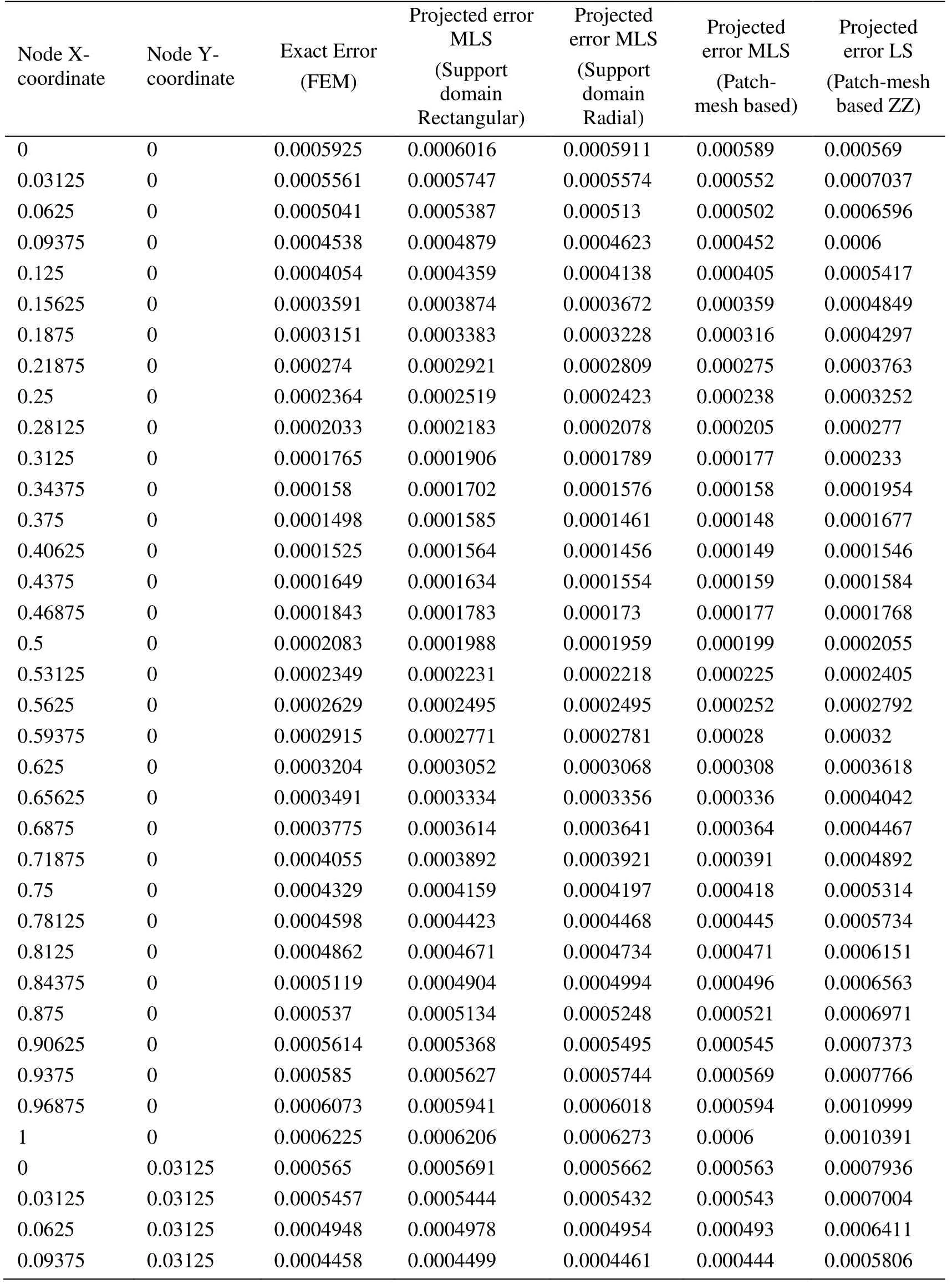
Node Xcoordinate Node Ycoordinate Exact Error (FEM) Projected error MLS (Support domain Rectangular) Projected error MLS (Support domain Radial) Projected error MLS (Patch- mesh based) Projected error LS (Patch-mesh based ZZ) 0 0 0.0005925 0.0006016 0.0005911 0.000589 0.000569 0.03125 0 0.0005561 0.0005747 0.0005574 0.000552 0.0007037 0.0625 0 0.0005041 0.0005387 0.000513 0.000502 0.0006596 0.09375 0 0.0004538 0.0004879 0.0004623 0.000452 0.0006 0.125 0 0.0004054 0.0004359 0.0004138 0.000405 0.0005417 0.15625 0 0.0003591 0.0003874 0.0003672 0.000359 0.0004849 0.1875 0 0.0003151 0.0003383 0.0003228 0.000316 0.0004297 0.21875 0 0.000274 0.0002921 0.0002809 0.000275 0.0003763 0.25 0 0.0002364 0.0002519 0.0002423 0.000238 0.0003252 0.28125 0 0.0002033 0.0002183 0.0002078 0.000205 0.000277 0.3125 0 0.0001765 0.0001906 0.0001789 0.000177 0.000233 0.34375 0 0.000158 0.0001702 0.0001576 0.000158 0.0001954 0.375 0 0.0001498 0.0001585 0.0001461 0.000148 0.0001677 0.40625 0 0.0001525 0.0001564 0.0001456 0.000149 0.0001546 0.4375 0 0.0001649 0.0001634 0.0001554 0.000159 0.0001584 0.46875 0 0.0001843 0.0001783 0.000173 0.000177 0.0001768 0.5 0 0.0002083 0.0001988 0.0001959 0.000199 0.0002055 0.53125 0 0.0002349 0.0002231 0.0002218 0.000225 0.0002405 0.5625 0 0.0002629 0.0002495 0.0002495 0.000252 0.0002792 0.59375 0 0.0002915 0.0002771 0.0002781 0.00028 0.00032 0.625 0 0.0003204 0.0003052 0.0003068 0.000308 0.0003618 0.65625 0 0.0003491 0.0003334 0.0003356 0.000336 0.0004042 0.6875 0 0.0003775 0.0003614 0.0003641 0.000364 0.0004467 0.71875 0 0.0004055 0.0003892 0.0003921 0.000391 0.0004892 0.75 0 0.0004329 0.0004159 0.0004197 0.000418 0.0005314 0.78125 0 0.0004598 0.0004423 0.0004468 0.000445 0.0005734 0.8125 0 0.0004862 0.0004671 0.0004734 0.000471 0.0006151 0.84375 0 0.0005119 0.0004904 0.0004994 0.000496 0.0006563 0.875 0 0.000537 0.0005134 0.0005248 0.000521 0.0006971 0.90625 0 0.0005614 0.0005368 0.0005495 0.000545 0.0007373 0.9375 0 0.000585 0.0005627 0.0005744 0.000569 0.0007766 0.96875 0 0.0006073 0.0005941 0.0006018 0.000594 0.0010999 1 0 0.0006225 0.0006206 0.0006273 0.0006 0.0010391 0 0.03125 0.000565 0.0005691 0.0005662 0.000563 0.0007936 0.03125 0.03125 0.0005457 0.0005444 0.0005432 0.000543 0.0007004 0.0625 0.03125 0.0004948 0.0004978 0.0004954 0.000493 0.0006411 0.09375 0.03125 0.0004458 0.0004499 0.0004461 0.000444 0.0005806

0.125 0.03125 0.0003986 0.0004012 0.0003988 0.000397 0.0005219 0.15625 0.03125 0.0003535 0.0003569 0.0003535 0.000352 0.0004651 0.1875 0.03125 0.0003107 0.0003143 0.0003106 0.000309 0.0004104 0.21875 0.03125 0.0002707 0.0002736 0.0002704 0.000269 0.0003583 0.25 0.03125 0.0002342 0.0002363 0.0002336 0.000233 0.0003093 0.28125 0.03125 0.0002021 0.0002043 0.0002012 0.000201 0.0002642 0.3125 0.03125 0.000176 0.0001785 0.0001747 0.000175 0.0002244 0.34375 0.03125 0.0001577 0.0001606 0.0001559 0.000156 0.000192 0.375 0.03125 0.000149 0.0001519 0.0001468 0.000148 0.0001698 0.40625 0.03125 0.0001505 0.0001529 0.0001481 0.000149 0.0001607 0.4375 0.03125 0.0001613 0.0001626 0.0001586 0.00016 0.0001663 0.46875 0.03125 0.0001789 0.0001793 0.0001763 0.000177 0.0001851 0.5 0.03125 0.0002012 0.0002008 0.0001988 0.000199 0.000213 0.53125 0.03125 0.0002262 0.0002253 0.0002239 0.000224 0.0002462 0.5625 0.03125 0.0002527 0.0002515 0.0002506 0.000251 0.0002823 0.59375 0.03125 0.00028 0.0002786 0.0002781 0.000278 0.0003198 0.625 0.03125 0.0003074 0.000306 0.0003057 0.000305 0.0003578 0.65625 0.03125 0.0003348 0.0003334 0.0003332 0.000333 0.000396 0.6875 0.03125 0.0003619 0.0003605 0.0003604 0.00036 0.000434 0.71875 0.03125 0.0003885 0.0003872 0.0003871 0.000386 0.0004716 0.75 0.03125 0.0004147 0.000413 0.0004134 0.000412 0.0005087 0.78125 0.03125 0.0004403 0.0004385 0.0004391 0.000438 0.0005452 0.8125 0.03125 0.0004654 0.0004645 0.0004643 0.000463 0.0005811 0.84375 0.03125 0.0004899 0.0004891 0.0004889 0.000487 0.0006164 0.875 0.03125 0.0005139 0.0005123 0.0005129 0.000511 0.000651 0.90625 0.03125 0.0005373 0.0005342 0.0005364 0.000534 0.000685 0.9375 0.03125 0.0005601 0.0005551 0.0005591 0.000557 0.0007181 0.96875 0.03125 0.0005824 0.000576 0.0005797 0.000579 0.0009572 1 0.03125 0.0006031 0.0005973 0.0006023 0.000595 0.001139 0 0.0625 0.0005223 0.0005332 0.000526 0.00052 0.0007994 0.03125 0.0625 0.0005044 0.0005056 0.000504 0.000503 0.0007049 0.0625 0.0625 0.000456 0.000456 0.0004558 0.000456 0.0004575 0.09375 0.0625 0.0004095 0.0004101 0.0004091 0.00041 0.000411 0.125 0.0625 0.000365 0.0003654 0.0003646 0.000365 0.0003665 0.15625 0.0625 0.0003226 0.0003239 0.0003222 0.000323 0.0003242 0.1875 0.0625 0.0002828 0.0002848 0.0002824 0.000283 0.0002845 0.21875 0.0625 0.0002459 0.0002474 0.0002455 0.000246 0.0002477 0.25 0.0625 0.0002128 0.0002111 0.0002124 0.000213 0.0002147 0.28125 0.0625 0.0001846 0.0001807 0.0001842 0.000184 0.0001866 0.3125 0.0625 0.0001628 0.0001566 0.0001624 0.000163 0.0001648 0.34375 0.0625 0.0001491 0.0001406 0.0001488 0.000149 0.000151 0.375 0.0625 0.0001448 0.0001344 0.0001445 0.000144 0.0001463 0.40625 0.0625 0.0001497 0.000138 0.0001494 0.000149 0.0001507

0.4375 0.0625 0.0001623 0.00015 0.0001621 0.000162 0.0001629 0.46875 0.0625 0.0001805 0.0001682 0.0001804 0.00018 0.0001807 0.5 0.0625 0.0002022 0.0001902 0.0002022 0.000202 0.0002022 0.53125 0.0625 0.0002259 0.0002145 0.0002259 0.000226 0.0002258 0.5625 0.0625 0.0002507 0.0002398 0.0002508 0.00025 0.0002505 0.59375 0.0625 0.0002759 0.0002656 0.000276 0.000276 0.0002756 0.625 0.0625 0.0003012 0.0002915 0.0003013 0.000301 0.0003008 0.65625 0.0625 0.0003262 0.0003171 0.0003263 0.000326 0.0003258 0.6875 0.0625 0.0003509 0.0003423 0.000351 0.000351 0.0003505 0.71875 0.0625 0.0003751 0.000367 0.0003752 0.000375 0.0003747 0.75 0.0625 0.0003988 0.0003913 0.0003989 0.000399 0.0003984 0.78125 0.0625 0.0004219 0.0004177 0.000422 0.000422 0.0004215 0.8125 0.0625 0.0004445 0.0004418 0.0004446 0.000444 0.000444 0.84375 0.0625 0.0004665 0.0004637 0.0004666 0.000466 0.000466 0.875 0.0625 0.000488 0.0004848 0.000488 0.000488 0.0004875 0.90625 0.0625 0.0005089 0.0005052 0.0005089 0.000509 0.0005084 0.9375 0.0625 0.0005294 0.0005256 0.0005296 0.000529 0.0005289 0.96875 0.0625 0.0005495 0.0005472 0.0005487 0.000549 0.0007509 1 0.0625 0.0005697 0.0005616 0.000566 0.000564 0.0008706 0 0.09375 0.0004801 0.0004887 0.0004836 0.000478 0.0007377 0.03125 0.09375 0.0004636 0.0004659 0.0004638 0.000462 0.0006497 0.0625 0.09375 0.0004178 0.0004181 0.0004174 0.000418 0.0004192 0.09375 0.09375 0.0003739 0.0003743 0.0003738 0.000374 0.0003754 0.125 0.09375 0.0003321 0.0003326 0.000332 0.000332 0.0003336 0.15625 0.09375 0.0002926 0.0002942 0.0002925 0.000293 0.0002942 0.1875 0.09375 0.0002558 0.00026 0.0002557 0.000256 0.0002575 0.21875 0.09375 0.0002224 0.0002298 0.0002222 0.000222 0.0002242 0.25 0.09375 0.000193 0.0002019 0.0001928 0.000193 0.0001949 0.28125 0.09375 0.0001691 0.0001798 0.0001688 0.000169 0.000171 0.3125 0.09375 0.0001519 0.0001644 0.0001516 0.000152 0.0001538 0.34375 0.09375 0.000143 0.0001557 0.0001426 0.000143 0.0001447 0.375 0.09375 0.0001428 0.0001543 0.0001424 0.000142 0.0001441 0.40625 0.09375 0.0001506 0.0001602 0.0001502 0.00015 0.0001515 0.4375 0.09375 0.0001646 0.0001724 0.0001642 0.000164 0.0001651 0.46875 0.09375 0.0001829 0.0001894 0.0001825 0.000183 0.000183 0.5 0.09375 0.0002037 0.0002096 0.0002034 0.000203 0.0002037 0.53125 0.09375 0.000226 0.0002315 0.0002257 0.000226 0.0002258 0.5625 0.09375 0.000249 0.0002542 0.0002487 0.000249 0.0002487 0.59375 0.09375 0.0002721 0.0002773 0.0002719 0.000272 0.0002718 0.625 0.09375 0.0002951 0.0003002 0.0002949 0.000295 0.0002948 0.65625 0.09375 0.0003178 0.0003228 0.0003177 0.000318 0.0003174 0.6875 0.09375 0.0003401 0.000345 0.0003399 0.00034 0.0003397 0.71875 0.09375 0.0003618 0.0003667 0.0003617 0.000362 0.0003614

0.75 0.09375 0.000383 0.0003877 0.0003829 0.000383 0.0003826 0.78125 0.09375 0.0004036 0.0004057 0.0004035 0.000403 0.0004032 0.8125 0.09375 0.0004237 0.0004247 0.0004235 0.000423 0.0004232 0.84375 0.09375 0.0004432 0.0004426 0.000443 0.000443 0.0004427 0.875 0.09375 0.0004621 0.0004602 0.0004619 0.000462 0.0004616 0.90625 0.09375 0.0004806 0.0004777 0.0004804 0.00048 0.0004801 0.9375 0.09375 0.0004987 0.0004961 0.0004988 0.000498 0.0004982 0.96875 0.09375 0.0005165 0.0005161 0.0005158 0.000516 0.0007037 1 0.09375 0.0005357 0.0005278 0.0005303 0.00053 0.0008148 0 0.125 0.0004385 0.0004426 0.000442 0.000437 0.0006764 0.03125 0.125 0.0004234 0.0004234 0.0004236 0.000422 0.0005951 0.0625 0.125 0.0003802 0.0003797 0.0003798 0.00038 0.0003816 0.09375 0.125 0.000339 0.0003395 0.0003389 0.000339 0.0003405 0.125 0.125 0.0003 0.000301 0.0002999 0.0003 0.0003016 0.15625 0.125 0.0002636 0.0002657 0.0002634 0.000264 0.0002652 0.1875 0.125 0.0002301 0.0002335 0.0002299 0.00023 0.0002318 0.21875 0.125 0.0002003 0.0002059 0.0002001 0.0002 0.000202 0.25 0.125 0.0001751 0.000183 0.0001748 0.000175 0.0001769 0.28125 0.125 0.0001557 0.0001672 0.0001554 0.000156 0.0001576 0.3125 0.125 0.0001435 0.0001578 0.0001432 0.000143 0.0001453 0.34375 0.125 0.0001393 0.0001558 0.0001389 0.000139 0.0001408 0.375 0.125 0.0001429 0.0001607 0.0001425 0.000143 0.000144 0.40625 0.125 0.000153 0.0001711 0.0001526 0.000153 0.0001537 0.4375 0.125 0.0001679 0.0001855 0.0001676 0.000168 0.0001682 0.46875 0.125 0.0001859 0.0002027 0.0001856 0.000186 0.000186 0.5 0.125 0.0002057 0.0002216 0.0002054 0.000205 0.0002056 0.53125 0.125 0.0002264 0.0002413 0.0002262 0.000226 0.0002262 0.5625 0.125 0.0002475 0.0002615 0.0002473 0.000247 0.0002472 0.59375 0.125 0.0002685 0.0002816 0.0002683 0.000268 0.0002681 0.625 0.125 0.0002893 0.0003016 0.0002891 0.000289 0.0002889 0.65625 0.125 0.0003096 0.0003212 0.0003094 0.000309 0.0003092 0.6875 0.125 0.0003294 0.0003403 0.0003293 0.000329 0.000329 0.71875 0.125 0.0003487 0.0003589 0.0003485 0.000348 0.0003482 0.75 0.125 0.0003673 0.0003775 0.0003672 0.000367 0.0003669 0.78125 0.125 0.0003854 0.0003937 0.0003853 0.000385 0.0003849 0.8125 0.125 0.0004029 0.0004057 0.0004027 0.000403 0.0004024 0.84375 0.125 0.0004199 0.0004205 0.0004197 0.00042 0.0004194 0.875 0.125 0.0004363 0.0004358 0.0004361 0.000436 0.0004358 0.90625 0.125 0.0004523 0.0004515 0.0004521 0.000452 0.0004518 0.9375 0.125 0.000468 0.0004677 0.0004681 0.000468 0.0004674 0.96875 0.125 0.0004833 0.0004841 0.0004826 0.000483 0.0006561 1 0.125 0.0005014 0.0004949 0.0004958 0.000495 0.0007585 0 0.15625 0.0003976 0.0004023 0.000401 0.000396 0.0006155

0.03125 0.15625 0.0003839 0.0003847 0.000384 0.000383 0.0005411 0.0625 0.15625 0.0003433 0.0003446 0.0003429 0.000343 0.0003447 0.09375 0.15625 0.0003049 0.0003077 0.0003048 0.000305 0.0003063 0.125 0.15625 0.0002688 0.0002718 0.0002687 0.000269 0.0002704 0.15625 0.15625 0.0002356 0.0002381 0.0002355 0.000236 0.0002372 0.1875 0.15625 0.0002057 0.000207 0.0002055 0.000206 0.0002073 0.21875 0.15625 0.0001799 0.0001802 0.0001797 0.00018 0.0001816 0.25 0.15625 0.0001592 0.000159 0.000159 0.000159 0.000161 0.28125 0.15625 0.0001449 0.0001446 0.0001446 0.000145 0.0001466 0.3125 0.15625 0.0001377 0.0001375 0.0001374 0.000137 0.0001393 0.34375 0.15625 0.000138 0.0001377 0.0001376 0.000138 0.0001392 0.375 0.15625 0.0001447 0.0001445 0.0001444 0.000144 0.0001456 0.40625 0.15625 0.0001566 0.0001564 0.0001563 0.000156 0.0001571 0.4375 0.15625 0.000172 0.0001717 0.0001717 0.000172 0.0001722 0.46875 0.15625 0.0001894 0.0001892 0.0001891 0.000189 0.0001894 0.5 0.15625 0.000208 0.0002078 0.0002077 0.000208 0.0002078 0.53125 0.15625 0.0002271 0.0002269 0.0002268 0.000227 0.0002268 0.5625 0.15625 0.0002462 0.000246 0.000246 0.000246 0.0002458 0.59375 0.15625 0.000265 0.0002649 0.0002648 0.000265 0.0002646 0.625 0.15625 0.0002835 0.0002834 0.0002833 0.000283 0.0002831 0.65625 0.15625 0.0003015 0.0003013 0.0003013 0.000301 0.000301 0.6875 0.15625 0.0003188 0.0003187 0.0003187 0.000319 0.0003183 0.71875 0.15625 0.0003356 0.0003355 0.0003354 0.000335 0.0003351 0.75 0.15625 0.0003517 0.0003517 0.0003516 0.000352 0.0003512 0.78125 0.15625 0.0003672 0.0003664 0.0003671 0.000367 0.0003667 0.8125 0.15625 0.0003822 0.0003802 0.000382 0.000382 0.0003817 0.84375 0.15625 0.0003966 0.0003935 0.0003964 0.000396 0.0003961 0.875 0.15625 0.0004105 0.0004069 0.0004103 0.00041 0.00041 0.90625 0.15625 0.000424 0.0004209 0.0004238 0.000424 0.0004235 0.9375 0.15625 0.0004372 0.0004353 0.0004373 0.000437 0.0004367 0.96875 0.15625 0.0004501 0.0004493 0.0004494 0.00045 0.0006084 1 0.15625 0.0004669 0.0004603 0.0004611 0.000461 0.0007019 0 0.1875 0.0003574 0.0003621 0.0003607 0.000357 0.000555 0.03125 0.1875 0.000345 0.000346 0.0003451 0.000344 0.0004877 0.0625 0.1875 0.0003072 0.000309 0.0003067 0.000307 0.0003086 0.09375 0.1875 0.0002716 0.0002773 0.0002715 0.000272 0.0002731 0.125 0.1875 0.0002387 0.000243 0.0002386 0.000239 0.0002402 0.15625 0.1875 0.0002089 0.0002113 0.0002088 0.000209 0.0002105 0.1875 0.1875 0.0001829 0.0001836 0.0001828 0.000183 0.0001846 0.21875 0.1875 0.0001616 0.0001614 0.0001614 0.000161 0.0001633 0.25 0.1875 0.000146 0.0001458 0.0001457 0.000146 0.0001477 0.28125 0.1875 0.0001369 0.0001366 0.0001366 0.000137 0.0001385 0.3125 0.1875 0.0001347 0.0001344 0.0001344 0.000134 0.000136

0.34375 0.1875 0.0001388 0.0001386 0.0001385 0.000139 0.0001399 0.375 0.1875 0.0001482 0.000148 0.0001479 0.000148 0.0001489 0.40625 0.1875 0.0001612 0.000161 0.0001609 0.000161 0.0001616 0.4375 0.1875 0.0001766 0.0001764 0.0001763 0.000176 0.0001767 0.46875 0.1875 0.0001932 0.000193 0.000193 0.000193 0.0001931 0.5 0.1875 0.0002104 0.0002103 0.0002102 0.00021 0.0002102 0.53125 0.1875 0.0002278 0.0002276 0.0002276 0.000228 0.0002275 0.5625 0.1875 0.0002449 0.0002448 0.0002447 0.000245 0.0002445 0.59375 0.1875 0.0002616 0.0002615 0.0002614 0.000261 0.0002612 0.625 0.1875 0.0002778 0.0002777 0.0002776 0.000278 0.0002773 0.65625 0.1875 0.0002934 0.0002933 0.0002932 0.000293 0.0002929 0.6875 0.1875 0.0003083 0.0003082 0.0003081 0.000308 0.0003078 0.71875 0.1875 0.0003225 0.0003224 0.0003224 0.000322 0.000322 0.75 0.1875 0.0003361 0.000336 0.000336 0.000336 0.0003356 0.78125 0.1875 0.0003491 0.0003483 0.0003489 0.000349 0.0003486 0.8125 0.1875 0.0003615 0.0003598 0.0003613 0.000361 0.000361 0.84375 0.1875 0.0003733 0.0003709 0.0003731 0.000373 0.0003728 0.875 0.1875 0.0003847 0.0003821 0.0003845 0.000384 0.0003842 0.90625 0.1875 0.0003957 0.0003937 0.0003955 0.000395 0.0003952 0.9375 0.1875 0.0004063 0.0004053 0.0004065 0.000406 0.0004058 0.96875 0.1875 0.0004168 0.0004165 0.000416 0.000416 0.0005606 1 0.1875 0.0004324 0.0004281 0.0004263 0.000426 0.0006452 0 0.21875 0.0003179 0.0003226 0.000321 0.000317 0.000495 0.03125 0.21875 0.000307 0.0003079 0.000307 0.000306 0.000435 0.0625 0.21875 0.0002719 0.0002733 0.0002714 0.000272 0.0002733 0.09375 0.21875 0.0002394 0.0002457 0.0002393 0.000239 0.0002408 0.125 0.21875 0.0002099 0.0002159 0.0002097 0.00021 0.0002114 0.15625 0.21875 0.0001839 0.000187 0.0001838 0.000184 0.0001855 0.1875 0.21875 0.0001623 0.0001635 0.0001621 0.000162 0.0001639 0.21875 0.21875 0.000146 0.000146 0.0001457 0.000146 0.0001476 0.25 0.21875 0.0001357 0.0001355 0.0001354 0.000135 0.0001373 0.28125 0.21875 0.0001319 0.0001317 0.0001316 0.000132 0.0001333 0.3125 0.21875 0.0001342 0.000134 0.0001339 0.000134 0.0001354 0.34375 0.21875 0.0001417 0.0001415 0.0001414 0.000141 0.0001425 0.375 0.21875 0.0001529 0.0001527 0.0001526 0.000153 0.0001534 0.40625 0.21875 0.0001665 0.0001663 0.0001663 0.000166 0.0001667 0.4375 0.21875 0.0001815 0.0001814 0.0001813 0.000181 0.0001815 0.46875 0.21875 0.0001972 0.000197 0.000197 0.000197 0.000197 0.5 0.21875 0.000213 0.0002128 0.0002127 0.000213 0.0002127 0.53125 0.21875 0.0002285 0.0002284 0.0002283 0.000228 0.0002282 0.5625 0.21875 0.0002436 0.0002435 0.0002435 0.000243 0.0002432 0.59375 0.21875 0.0002582 0.0002581 0.000258 0.000258 0.0002578 0.625 0.21875 0.0002721 0.000272 0.0002719 0.000272 0.0002716

0.65625 0.21875 0.0002853 0.0002852 0.0002851 0.000285 0.0002848 0.6875 0.21875 0.0002978 0.0002977 0.0002976 0.000298 0.0002973 0.71875 0.21875 0.0003095 0.0003094 0.0003094 0.000309 0.000309 0.75 0.21875 0.0003206 0.0003205 0.0003204 0.00032 0.0003201 0.78125 0.21875 0.000331 0.0003307 0.0003308 0.000331 0.0003305 0.8125 0.21875 0.0003408 0.0003405 0.0003406 0.000341 0.0003403 0.84375 0.21875 0.0003501 0.0003501 0.0003499 0.00035 0.0003496 0.875 0.21875 0.0003589 0.0003593 0.0003587 0.000359 0.0003584 0.90625 0.21875 0.0003673 0.0003681 0.0003671 0.000367 0.0003668 0.9375 0.21875 0.0003755 0.0003767 0.0003756 0.000375 0.000375 0.96875 0.21875 0.0003835 0.000385 0.0003827 0.000383 0.0005127 1 0.21875 0.0003977 0.0003952 0.0003914 0.000391 0.0005885 0 0.25 0.0002793 0.000284 0.0002822 0.000279 0.0004355 0.03125 0.25 0.0002699 0.0002707 0.0002698 0.000269 0.0003831 0.0625 0.25 0.0002377 0.0002376 0.0002372 0.000238 0.0002391 0.09375 0.25 0.0002085 0.0002119 0.0002083 0.000208 0.0002099 0.125 0.25 0.0001827 0.0001851 0.0001825 0.000183 0.0001841 0.15625 0.25 0.000161 0.0001611 0.0001608 0.000161 0.0001626 0.1875 0.25 0.0001444 0.0001445 0.0001442 0.000144 0.000146 0.21875 0.25 0.0001335 0.0001335 0.0001333 0.000133 0.0001351 0.25 0.25 0.0001288 0.0001286 0.0001286 0.000129 0.0001303 0.28125 0.25 0.00013 0.0001298 0.0001298 0.00013 0.0001312 0.3125 0.25 0.0001363 0.0001361 0.000136 0.000136 0.0001371 0.34375 0.25 0.0001462 0.000146 0.0001459 0.000146 0.0001468 0.375 0.25 0.0001586 0.0001584 0.0001583 0.000158 0.0001589 0.40625 0.25 0.0001723 0.0001722 0.0001721 0.000172 0.0001724 0.4375 0.25 0.0001867 0.0001866 0.0001865 0.000186 0.0001866 0.46875 0.25 0.0002012 0.0002011 0.000201 0.000201 0.000201 0.5 0.25 0.0002154 0.0002153 0.0002152 0.000215 0.0002151 0.53125 0.25 0.0002292 0.0002291 0.000229 0.000229 0.0002288 0.5625 0.25 0.0002423 0.0002422 0.0002421 0.000242 0.0002419 0.59375 0.25 0.0002547 0.0002546 0.0002546 0.000255 0.0002543 0.625 0.25 0.0002664 0.0002663 0.0002662 0.000266 0.0002659 0.65625 0.25 0.0002772 0.0002771 0.0002771 0.000277 0.0002767 0.6875 0.25 0.0002873 0.0002872 0.0002871 0.000287 0.0002868 0.71875 0.25 0.0002966 0.0002964 0.0002964 0.000296 0.000296 0.75 0.25 0.0003051 0.000305 0.0003049 0.000305 0.0003046 0.78125 0.25 0.0003129 0.0003129 0.0003128 0.000313 0.0003124 0.8125 0.25 0.0003202 0.0003205 0.00032 0.00032 0.0003197 0.84375 0.25 0.0003268 0.0003279 0.0003267 0.000327 0.0003263 0.875 0.25 0.0003331 0.0003347 0.0003329 0.000333 0.0003326 0.90625 0.25 0.000339 0.0003409 0.0003388 0.000339 0.0003385 0.9375 0.25 0.0003446 0.0003464 0.0003447 0.000344 0.0003442

0.96875 0.25 0.0003502 0.0003518 0.0003494 0.00035 0.0004648 1 0.25 0.0003631 0.0003614 0.0003566 0.000357 0.0005317 0 0.28125 0.0002419 0.0002465 0.0002445 0.000242 0.0003767 0.03125 0.28125 0.0002339 0.0002347 0.0002337 0.000233 0.0003323 0.0625 0.28125 0.0002049 0.0002042 0.0002044 0.000205 0.0002062 0.09375 0.28125 0.0001793 0.0001826 0.0001791 0.000179 0.0001807 0.125 0.28125 0.0001577 0.0001611 0.0001575 0.000158 0.0001592 0.15625 0.28125 0.000141 0.0001408 0.0001408 0.000141 0.0001425 0.1875 0.28125 0.00013 0.0001297 0.0001297 0.00013 0.0001315 0.21875 0.28125 0.0001249 0.0001247 0.0001246 0.000125 0.0001263 0.25 0.28125 0.0001256 0.0001254 0.0001253 0.000125 0.0001269 0.28125 0.28125 0.0001312 0.000131 0.000131 0.000131 0.0001322 0.3125 0.28125 0.0001404 0.0001403 0.0001402 0.00014 0.0001411 0.34375 0.28125 0.000152 0.0001519 0.0001518 0.000152 0.0001524 0.375 0.28125 0.0001649 0.0001648 0.0001647 0.000165 0.0001651 0.40625 0.28125 0.0001784 0.0001783 0.0001782 0.000178 0.0001784 0.4375 0.28125 0.0001919 0.0001918 0.0001917 0.000192 0.0001918 0.46875 0.28125 0.0002051 0.000205 0.0002049 0.000205 0.0002048 0.5 0.28125 0.0002178 0.0002177 0.0002176 0.000218 0.0002174 0.53125 0.28125 0.0002297 0.0002296 0.0002295 0.00023 0.0002293 0.5625 0.28125 0.0002409 0.0002408 0.0002407 0.000241 0.0002404 0.59375 0.28125 0.0002512 0.0002511 0.000251 0.000251 0.0002507 0.625 0.28125 0.0002606 0.0002605 0.0002604 0.00026 0.0002601 0.65625 0.28125 0.0002691 0.000269 0.0002689 0.000269 0.0002686 0.6875 0.28125 0.0002767 0.0002766 0.0002766 0.000277 0.0002762 0.71875 0.28125 0.0002836 0.0002835 0.0002834 0.000283 0.000283 0.75 0.28125 0.0002896 0.0002895 0.0002894 0.000289 0.0002891 0.78125 0.28125 0.0002949 0.0002949 0.0002947 0.000295 0.0002944 0.8125 0.28125 0.0002996 0.0002995 0.0002994 0.000299 0.0002991 0.84375 0.28125 0.0003037 0.0003036 0.0003035 0.000303 0.0003032 0.875 0.28125 0.0003073 0.000307 0.0003071 0.000307 0.0003069 0.90625 0.28125 0.0003107 0.00031 0.0003104 0.00031 0.0003102 0.9375 0.28125 0.0003138 0.0003132 0.0003139 0.000314 0.0003134 0.96875 0.28125 0.000317 0.0003166 0.0003161 0.000316 0.0004169 1 0.28125 0.0003285 0.0003233 0.0003219 0.000322 0.000475 0 0.3125 0.0002061 0.0002104 0.0002081 0.000206 0.0003189 0.03125 0.3125 0.0001994 0.0002003 0.0001992 0.000198 0.0002828 0.0625 0.3125 0.000174 0.0001725 0.0001735 0.000174 0.0001753 0.09375 0.3125 0.0001525 0.0001566 0.0001523 0.000152 0.0001539 0.125 0.3125 0.0001359 0.0001403 0.0001357 0.000136 0.0001374 0.15625 0.3125 0.0001249 0.0001247 0.0001247 0.000125 0.0001264 0.1875 0.3125 0.0001199 0.0001197 0.0001196 0.00012 0.0001213 0.21875 0.3125 0.0001206 0.0001204 0.0001204 0.00012 0.0001219

0.25 0.3125 0.0001261 0.0001259 0.0001259 0.000126 0.0001271 0.28125 0.3125 0.0001352 0.000135 0.0001349 0.000135 0.0001359 0.3125 0.3125 0.0001464 0.0001463 0.0001462 0.000146 0.0001469 0.34375 0.3125 0.0001589 0.0001588 0.0001587 0.000159 0.0001591 0.375 0.3125 0.0001718 0.0001717 0.0001716 0.000172 0.0001718 0.40625 0.3125 0.0001847 0.0001846 0.0001845 0.000184 0.0001845 0.4375 0.3125 0.0001971 0.000197 0.0001969 0.000197 0.0001969 0.46875 0.3125 0.0002089 0.0002088 0.0002088 0.000209 0.0002086 0.5 0.3125 0.00022 0.0002198 0.0002198 0.00022 0.0002195 0.53125 0.3125 0.0002301 0.00023 0.0002299 0.00023 0.0002296 0.5625 0.3125 0.0002392 0.0002391 0.0002391 0.000239 0.0002388 0.59375 0.3125 0.0002474 0.0002473 0.0002473 0.000247 0.0002469 0.625 0.3125 0.0002547 0.0002546 0.0002545 0.000254 0.0002541 0.65625 0.3125 0.0002609 0.0002608 0.0002607 0.000261 0.0002604 0.6875 0.3125 0.0002662 0.0002661 0.000266 0.000266 0.0002657 0.71875 0.3125 0.0002706 0.0002705 0.0002704 0.00027 0.0002701 0.75 0.3125 0.0002741 0.0002741 0.000274 0.000274 0.0002736 0.78125 0.3125 0.0002769 0.0002769 0.0002767 0.000277 0.0002764 0.8125 0.3125 0.000279 0.000279 0.0002788 0.000279 0.0002785 0.84375 0.3125 0.0002806 0.0002805 0.0002804 0.00028 0.0002801 0.875 0.3125 0.0002817 0.0002813 0.0002814 0.000281 0.0002812 0.90625 0.3125 0.0002825 0.0002818 0.0002822 0.000282 0.0002821 0.9375 0.3125 0.0002832 0.0002824 0.0002833 0.000283 0.0002828 0.96875 0.3125 0.0002839 0.0002835 0.000283 0.000283 0.0003692 1 0.3125 0.0002942 0.0002888 0.0002873 0.000288 0.0004185 0 0.34375 0.0001724 0.0001763 0.0001737 0.000172 0.0002624 0.03125 0.34375 0.0001673 0.0001681 0.0001669 0.000166 0.0002355 0.0625 0.34375 0.0001459 0.0001435 0.0001454 0.000146 0.0001472 0.09375 0.34375 0.0001294 0.0001342 0.0001291 0.000129 0.0001308 0.125 0.34375 0.0001187 0.0001242 0.0001184 0.000118 0.0001201 0.15625 0.34375 0.000114 0.0001137 0.0001137 0.000114 0.0001154 0.1875 0.34375 0.0001151 0.0001148 0.0001148 0.000115 0.0001163 0.21875 0.34375 0.0001209 0.0001207 0.0001206 0.000121 0.0001219 0.25 0.34375 0.0001301 0.0001299 0.0001299 0.00013 0.0001309 0.28125 0.34375 0.0001415 0.0001413 0.0001412 0.000141 0.0001419 0.3125 0.34375 0.0001538 0.0001537 0.0001536 0.000154 0.0001541 0.34375 0.34375 0.0001665 0.0001664 0.0001663 0.000166 0.0001666 0.375 0.34375 0.000179 0.0001789 0.0001788 0.000179 0.0001789 0.40625 0.34375 0.000191 0.0001909 0.0001908 0.000191 0.0001908 0.4375 0.34375 0.0002022 0.0002021 0.000202 0.000202 0.0002019 0.46875 0.34375 0.0002125 0.0002124 0.0002124 0.000212 0.0002121 0.5 0.34375 0.0002219 0.0002218 0.0002217 0.000222 0.0002214 0.53125 0.34375 0.0002302 0.0002301 0.00023 0.00023 0.0002297

0.5625 0.34375 0.0002374 0.0002373 0.0002372 0.000237 0.0002369 0.59375 0.34375 0.0002435 0.0002434 0.0002434 0.000243 0.000243 0.625 0.34375 0.0002486 0.0002485 0.0002484 0.000248 0.0002481 0.65625 0.34375 0.0002526 0.0002525 0.0002524 0.000252 0.0002521 0.6875 0.34375 0.0002556 0.0002555 0.0002554 0.000255 0.0002551 0.71875 0.34375 0.0002576 0.0002575 0.0002574 0.000257 0.0002571 0.75 0.34375 0.0002587 0.0002586 0.0002585 0.000259 0.0002582 0.78125 0.34375 0.000259 0.000259 0.0002588 0.000259 0.0002585 0.8125 0.34375 0.0002586 0.0002586 0.0002584 0.000258 0.0002581 0.84375 0.34375 0.0002576 0.0002575 0.0002574 0.000257 0.0002572 0.875 0.34375 0.0002562 0.0002558 0.0002559 0.000256 0.0002558 0.90625 0.34375 0.0002545 0.0002537 0.0002542 0.000254 0.0002541 0.9375 0.34375 0.0002527 0.0002519 0.0002528 0.000252 0.0002524 0.96875 0.34375 0.0002512 0.0002507 0.0002502 0.000251 0.0003218 1 0.34375 0.0002601 0.0002546 0.000253 0.000254 0.0003623 0 0.375 0.0001423 0.0001454 0.0001424 0.000141 0.0002083 0.03125 0.375 0.0001387 0.0001394 0.0001381 0.000137 0.0001914 0.0625 0.375 0.0001224 0.0001186 0.0001218 0.000122 0.0001236 0.09375 0.375 0.0001119 0.000117 0.0001115 0.000112 0.0001132 0.125 0.375 0.0001077 0.0001144 0.0001073 0.000107 0.000109 0.15625 0.375 0.0001094 0.0001091 0.000109 0.000109 0.0001106 0.1875 0.375 0.0001158 0.0001155 0.0001155 0.000115 0.0001168 0.21875 0.375 0.0001255 0.0001253 0.0001252 0.000125 0.0001263 0.25 0.375 0.0001372 0.000137 0.0001369 0.000137 0.0001377 0.28125 0.375 0.0001497 0.0001495 0.0001495 0.000149 0.0001499 0.3125 0.375 0.0001624 0.0001622 0.0001621 0.000162 0.0001624 0.34375 0.375 0.0001747 0.0001746 0.0001745 0.000174 0.0001746 0.375 0.375 0.0001864 0.0001863 0.0001862 0.000186 0.0001862 0.40625 0.375 0.0001972 0.0001971 0.0001971 0.000197 0.0001969 0.4375 0.375 0.0002071 0.000207 0.0002069 0.000207 0.0002067 0.46875 0.375 0.0002159 0.0002158 0.0002157 0.000216 0.0002154 0.5 0.375 0.0002235 0.0002234 0.0002233 0.000223 0.000223 0.53125 0.375 0.00023 0.0002299 0.0002298 0.00023 0.0002295 0.5625 0.375 0.0002353 0.0002352 0.0002351 0.000235 0.0002348 0.59375 0.375 0.0002394 0.0002393 0.0002392 0.000239 0.0002389 0.625 0.375 0.0002424 0.0002423 0.0002422 0.000242 0.0002418 0.65625 0.375 0.0002442 0.0002441 0.000244 0.000244 0.0002437 0.6875 0.375 0.0002449 0.0002448 0.0002448 0.000245 0.0002444 0.71875 0.375 0.0002447 0.0002445 0.0002445 0.000244 0.0002441 0.75 0.375 0.0002434 0.0002433 0.0002432 0.000243 0.0002429 0.78125 0.375 0.0002412 0.0002412 0.0002411 0.000241 0.0002408 0.8125 0.375 0.0002383 0.0002384 0.0002381 0.000238 0.0002379 0.84375 0.375 0.0002348 0.0002348 0.0002346 0.000235 0.0002345

0.15625 0.4375 0.00012 0.0001198 0.0001197 0.00012 0.0001208 0.1875 0.4375 0.0001323 0.0001321 0.000132 0.000132 0.0001328 0.21875 0.4375 0.0001452 0.000145 0.0001449 0.000145 0.0001454 0.25 0.4375 0.0001579 0.0001578 0.0001577 0.000158 0.000158 0.28125 0.4375 0.0001701 0.00017 0.0001699 0.00017 0.00017 0.3125 0.4375 0.0001815 0.0001814 0.0001813 0.000181 0.0001813 0.34375 0.4375 0.0001919 0.0001918 0.0001917 0.000192 0.0001916 0.375 0.4375 0.0002012 0.0002011 0.000201 0.000201 0.0002008 0.40625 0.4375 0.0002093 0.0002092 0.0002091 0.000209 0.0002088 0.4375 0.4375 0.0002161 0.000216 0.0002159 0.000216 0.0002156 0.46875 0.4375 0.0002216 0.0002215 0.0002214 0.000221 0.0002211 0.5 0.4375 0.0002258 0.0002257 0.0002256 0.000226 0.0002253 0.53125 0.4375 0.0002286 0.0002285 0.0002285 0.000228 0.0002281 0.5625 0.4375 0.0002302 0.0002301 0.00023 0.00023 0.0002297 0.59375 0.4375 0.0002304 0.0002303 0.0002303 0.00023 0.0002299 0.625 0.4375 0.0002294 0.0002293 0.0002292 0.000229 0.0002289 0.65625 0.4375 0.0002271 0.000227 0.0002269 0.000227 0.0002266 0.6875 0.4375 0.0002236 0.0002235 0.0002234 0.000223 0.0002231 0.71875 0.4375 0.0002189 0.0002188 0.0002187 0.000219 0.0002185 0.75 0.4375 0.0002132 0.0002131 0.000213 0.000213 0.0002128 0.78125 0.4375 0.0002064 0.0002064 0.0002062 0.000206 0.0002061 0.8125 0.4375 0.0001989 0.0001989 0.0001987 0.000199 0.0001986 0.84375 0.4375 0.0001907 0.0001907 0.0001905 0.00019 0.0001905 0.875 0.4375 0.0001822 0.0001817 0.0001819 0.000182 0.0001821 0.90625 0.4375 0.0001736 0.0001726 0.0001733 0.000173 0.0001737 0.9375 0.4375 0.0001655 0.0001644 0.0001656 0.000165 0.0001658 0.96875 0.4375 0.0001585 0.0001578 0.0001572 0.000158 0.0001861 1 0.4375 0.0001634 0.0001575 0.0001555 0.000157 0.0001998 0 0.46875 0.000102 0.0000988 0.0000961 9.78E-05 0.0001022 0.03125 0.46875 0.0001011 0.0001009 0.0000997 9.97E-05 0.0001119 0.0625 0.46875 0.0001038 0.0000973 0.0001034 0.000103 0.000105 0.09375 0.46875 0.0001112 0.0001136 0.0001107 0.000111 0.0001121 0.125 0.46875 0.0001215 0.0001292 0.0001212 0.000121 0.0001222 0.15625 0.46875 0.0001335 0.0001333 0.0001332 0.000133 0.000134 0.1875 0.46875 0.0001461 0.0001459 0.0001459 0.000146 0.0001463 0.21875 0.46875 0.0001586 0.0001584 0.0001584 0.000158 0.0001587 0.25 0.46875 0.0001706 0.0001704 0.0001703 0.00017 0.0001705 0.28125 0.46875 0.0001817 0.0001815 0.0001815 0.000181 0.0001815 0.3125 0.46875 0.0001918 0.0001917 0.0001916 0.000192 0.0001915 0.34375 0.46875 0.0002007 0.0002006 0.0002006 0.000201 0.0002004 0.375 0.46875 0.0002085 0.0002084 0.0002083 0.000208 0.0002081 0.40625 0.46875 0.0002149 0.0002148 0.0002148 0.000215 0.0002145 0.4375 0.46875 0.0002201 0.00022 0.0002199 0.00022 0.0002196

0.46875 0.46875 0.0002239 0.0002238 0.0002237 0.000224 0.0002234 0.5 0.46875 0.0002263 0.0002263 0.0002262 0.000226 0.0002258 0.53125 0.46875 0.0002274 0.0002273 0.0002273 0.000227 0.0002269 0.5625 0.46875 0.0002272 0.0002271 0.000227 0.000227 0.0002266 0.59375 0.46875 0.0002255 0.0002255 0.0002254 0.000225 0.000225 0.625 0.46875 0.0002226 0.0002225 0.0002224 0.000222 0.0002221 0.65625 0.46875 0.0002184 0.0002183 0.0002182 0.000218 0.0002179 0.6875 0.46875 0.0002129 0.0002128 0.0002127 0.000213 0.0002125 0.71875 0.46875 0.0002062 0.0002061 0.000206 0.000206 0.0002058 0.75 0.46875 0.0001984 0.0001983 0.0001982 0.000198 0.0001981 0.78125 0.46875 0.0001897 0.0001896 0.0001894 0.000189 0.0001894 0.8125 0.46875 0.0001801 0.0001801 0.0001798 0.00018 0.0001799 0.84375 0.46875 0.0001699 0.0001698 0.0001696 0.00017 0.0001699 0.875 0.46875 0.0001595 0.000159 0.0001592 0.000159 0.0001596 0.90625 0.46875 0.0001492 0.0001481 0.0001489 0.000149 0.0001496 0.9375 0.46875 0.0001399 0.0001386 0.0001399 0.000139 0.0001404 0.96875 0.46875 0.0001324 0.0001315 0.0001309 0.000131 0.0001477 1 0.46875 0.0001358 0.00013 0.0001279 0.00013 0.0001521 0 0.5 0.0001141 0.0001083 0.0001066 0.000109 0.0001156 0.03125 0.5 0.000112 0.0001114 0.0001105 0.000111 0.0001202 0.0625 0.5 0.0001184 0.0001122 0.0001182 0.000118 0.0001193 0.09375 0.5 0.0001278 0.0001297 0.0001274 0.000127 0.0001284 0.125 0.5 0.0001388 0.0001458 0.0001385 0.000138 0.0001392 0.15625 0.5 0.0001506 0.0001503 0.0001503 0.00015 0.0001507 0.1875 0.5 0.0001623 0.0001621 0.0001621 0.000162 0.0001623 0.21875 0.5 0.0001736 0.0001734 0.0001734 0.000173 0.0001735 0.25 0.5 0.0001842 0.000184 0.000184 0.000184 0.0001839 0.28125 0.5 0.0001938 0.0001936 0.0001936 0.000194 0.0001935 0.3125 0.5 0.0002023 0.0002021 0.0002021 0.000202 0.0002019 0.34375 0.5 0.0002096 0.0002095 0.0002094 0.000209 0.0002092 0.375 0.5 0.0002156 0.0002155 0.0002155 0.000215 0.0002152 0.40625 0.5 0.0002204 0.0002203 0.0002202 0.00022 0.0002199 0.4375 0.5 0.0002238 0.0002237 0.0002236 0.000224 0.0002233 0.46875 0.5 0.0002258 0.0002258 0.0002257 0.000226 0.0002253 0.5 0.5 0.0002265 0.0002264 0.0002264 0.000226 0.000226 0.53125 0.5 0.0002258 0.0002258 0.0002257 0.000226 0.0002253 0.5625 0.5 0.0002238 0.0002237 0.0002236 0.000224 0.0002233 0.59375 0.5 0.0002204 0.0002203 0.0002202 0.00022 0.0002199 0.625 0.5 0.0002156 0.0002155 0.0002155 0.000215 0.0002152 0.65625 0.5 0.0002096 0.0002095 0.0002094 0.000209 0.0002092 0.6875 0.5 0.0002023 0.0002021 0.0002021 0.000202 0.0002019 0.71875 0.5 0.0001938 0.0001936 0.0001936 0.000194 0.0001935 0.75 0.5 0.0001842 0.0001841 0.000184 0.000184 0.0001839

0.78125 0.5 0.0001736 0.0001736 0.0001734 0.000173 0.0001735 0.8125 0.5 0.0001623 0.0001623 0.0001621 0.000162 0.0001623 0.84375 0.5 0.0001506 0.0001505 0.0001503 0.00015 0.0001507 0.875 0.5 0.0001388 0.0001383 0.0001385 0.000138 0.0001392 0.90625 0.5 0.0001278 0.0001264 0.0001274 0.000127 0.0001284 0.9375 0.5 0.0001184 0.0001169 0.0001182 0.000118 0.0001193 0.96875 0.5 0.000112 0.0001111 0.0001105 0.000111 0.0001202 1 0.5 0.0001141 0.0001089 0.0001066 0.000109 0.0001156 0 0.53125 0.0001358 0.0001288 0.0001279 0.00013 0.0001521 0.03125 0.53125 0.0001324 0.0001316 0.0001309 0.000131 0.0001477 0.0625 0.53125 0.0001399 0.0001343 0.0001399 0.000139 0.0001404 0.09375 0.53125 0.0001492 0.000151 0.0001489 0.000149 0.0001496 0.125 0.53125 0.0001595 0.0001658 0.0001592 0.000159 0.0001596 0.15625 0.53125 0.0001699 0.0001697 0.0001696 0.00017 0.0001699 0.1875 0.53125 0.0001801 0.0001799 0.0001798 0.00018 0.0001799 0.21875 0.53125 0.0001897 0.0001895 0.0001894 0.000189 0.0001894 0.25 0.53125 0.0001984 0.0001983 0.0001982 0.000198 0.0001981 0.28125 0.53125 0.0002062 0.0002061 0.000206 0.000206 0.0002058 0.3125 0.53125 0.0002129 0.0002128 0.0002127 0.000213 0.0002125 0.34375 0.53125 0.0002184 0.0002183 0.0002182 0.000218 0.0002179 0.375 0.53125 0.0002226 0.0002225 0.0002224 0.000222 0.0002221 0.40625 0.53125 0.0002255 0.0002255 0.0002254 0.000225 0.000225 0.4375 0.53125 0.0002272 0.0002271 0.000227 0.000227 0.0002266 0.46875 0.53125 0.0002274 0.0002273 0.0002273 0.000227 0.0002269 0.5 0.53125 0.0002263 0.0002263 0.0002262 0.000226 0.0002258 0.53125 0.53125 0.0002239 0.0002238 0.0002237 0.000224 0.0002234 0.5625 0.53125 0.0002201 0.00022 0.0002199 0.00022 0.0002196 0.59375 0.53125 0.0002149 0.0002148 0.0002148 0.000215 0.0002145 0.625 0.53125 0.0002085 0.0002084 0.0002083 0.000208 0.0002081 0.65625 0.53125 0.0002007 0.0002006 0.0002006 0.000201 0.0002004 0.6875 0.53125 0.0001918 0.0001917 0.0001916 0.000192 0.0001915 0.71875 0.53125 0.0001817 0.0001815 0.0001815 0.000181 0.0001815 0.75 0.53125 0.0001706 0.0001705 0.0001703 0.00017 0.0001705 0.78125 0.53125 0.0001586 0.0001586 0.0001584 0.000158 0.0001587 0.8125 0.53125 0.0001461 0.0001461 0.0001459 0.000146 0.0001463 0.84375 0.53125 0.0001335 0.0001335 0.0001332 0.000133 0.000134 0.875 0.53125 0.0001215 0.0001209 0.0001212 0.000121 0.0001222 0.90625 0.53125 0.0001112 0.0001097 0.0001107 0.000111 0.0001121 0.9375 0.53125 0.0001038 0.0001022 0.0001034 0.000103 0.000105 0.96875 0.53125 0.0001011 0.0001002 0.0000997 9.97E-05 0.0001119 1 0.53125 0.000102 0.0000984 0.0000961 9.78E-05 0.0001022 0 0.5625 0.0001634 0.000156 0.0001555 0.000157 0.0001998 0.03125 0.5625 0.0001585 0.0001577 0.0001572 0.000158 0.0001861

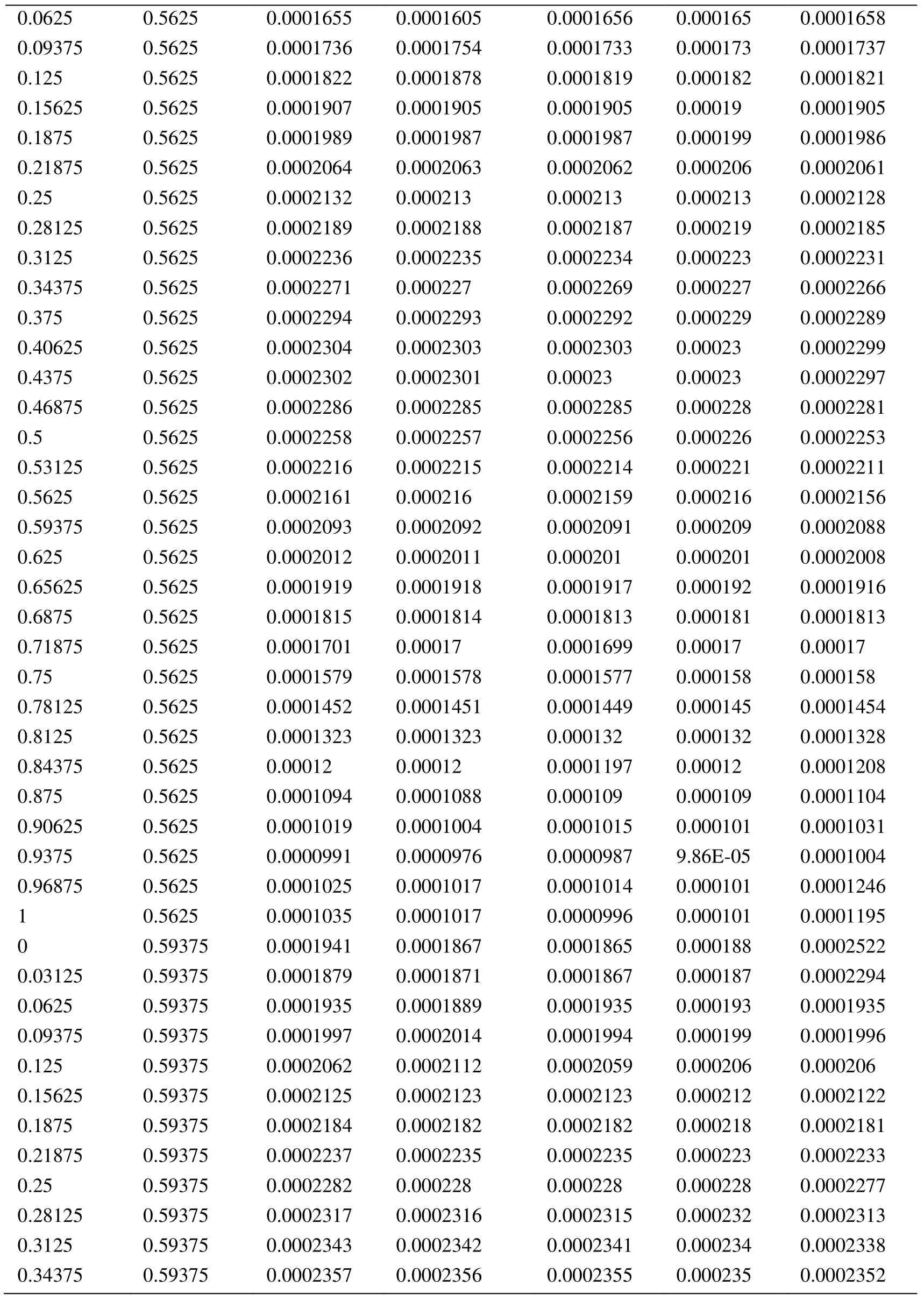
0.0625 0.5625 0.0001655 0.0001605 0.0001656 0.000165 0.0001658 0.09375 0.5625 0.0001736 0.0001754 0.0001733 0.000173 0.0001737 0.125 0.5625 0.0001822 0.0001878 0.0001819 0.000182 0.0001821 0.15625 0.5625 0.0001907 0.0001905 0.0001905 0.00019 0.0001905 0.1875 0.5625 0.0001989 0.0001987 0.0001987 0.000199 0.0001986 0.21875 0.5625 0.0002064 0.0002063 0.0002062 0.000206 0.0002061 0.25 0.5625 0.0002132 0.000213 0.000213 0.000213 0.0002128 0.28125 0.5625 0.0002189 0.0002188 0.0002187 0.000219 0.0002185 0.3125 0.5625 0.0002236 0.0002235 0.0002234 0.000223 0.0002231 0.34375 0.5625 0.0002271 0.000227 0.0002269 0.000227 0.0002266 0.375 0.5625 0.0002294 0.0002293 0.0002292 0.000229 0.0002289 0.40625 0.5625 0.0002304 0.0002303 0.0002303 0.00023 0.0002299 0.4375 0.5625 0.0002302 0.0002301 0.00023 0.00023 0.0002297 0.46875 0.5625 0.0002286 0.0002285 0.0002285 0.000228 0.0002281 0.5 0.5625 0.0002258 0.0002257 0.0002256 0.000226 0.0002253 0.53125 0.5625 0.0002216 0.0002215 0.0002214 0.000221 0.0002211 0.5625 0.5625 0.0002161 0.000216 0.0002159 0.000216 0.0002156 0.59375 0.5625 0.0002093 0.0002092 0.0002091 0.000209 0.0002088 0.625 0.5625 0.0002012 0.0002011 0.000201 0.000201 0.0002008 0.65625 0.5625 0.0001919 0.0001918 0.0001917 0.000192 0.0001916 0.6875 0.5625 0.0001815 0.0001814 0.0001813 0.000181 0.0001813 0.71875 0.5625 0.0001701 0.00017 0.0001699 0.00017 0.00017 0.75 0.5625 0.0001579 0.0001578 0.0001577 0.000158 0.000158 0.78125 0.5625 0.0001452 0.0001451 0.0001449 0.000145 0.0001454 0.8125 0.5625 0.0001323 0.0001323 0.000132 0.000132 0.0001328 0.84375 0.5625 0.00012 0.00012 0.0001197 0.00012 0.0001208 0.875 0.5625 0.0001094 0.0001088 0.000109 0.000109 0.0001104 0.90625 0.5625 0.0001019 0.0001004 0.0001015 0.000101 0.0001031 0.9375 0.5625 0.0000991 0.0000976 0.0000987 9.86E-05 0.0001004 0.96875 0.5625 0.0001025 0.0001017 0.0001014 0.000101 0.0001246 1 0.5625 0.0001035 0.0001017 0.0000996 0.000101 0.0001195 0 0.59375 0.0001941 0.0001867 0.0001865 0.000188 0.0002522 0.03125 0.59375 0.0001879 0.0001871 0.0001867 0.000187 0.0002294 0.0625 0.59375 0.0001935 0.0001889 0.0001935 0.000193 0.0001935 0.09375 0.59375 0.0001997 0.0002014 0.0001994 0.000199 0.0001996 0.125 0.59375 0.0002062 0.0002112 0.0002059 0.000206 0.000206 0.15625 0.59375 0.0002125 0.0002123 0.0002123 0.000212 0.0002122 0.1875 0.59375 0.0002184 0.0002182 0.0002182 0.000218 0.0002181 0.21875 0.59375 0.0002237 0.0002235 0.0002235 0.000223 0.0002233 0.25 0.59375 0.0002282 0.000228 0.000228 0.000228 0.0002277 0.28125 0.59375 0.0002317 0.0002316 0.0002315 0.000232 0.0002313 0.3125 0.59375 0.0002343 0.0002342 0.0002341 0.000234 0.0002338 0.34375 0.59375 0.0002357 0.0002356 0.0002355 0.000235 0.0002352

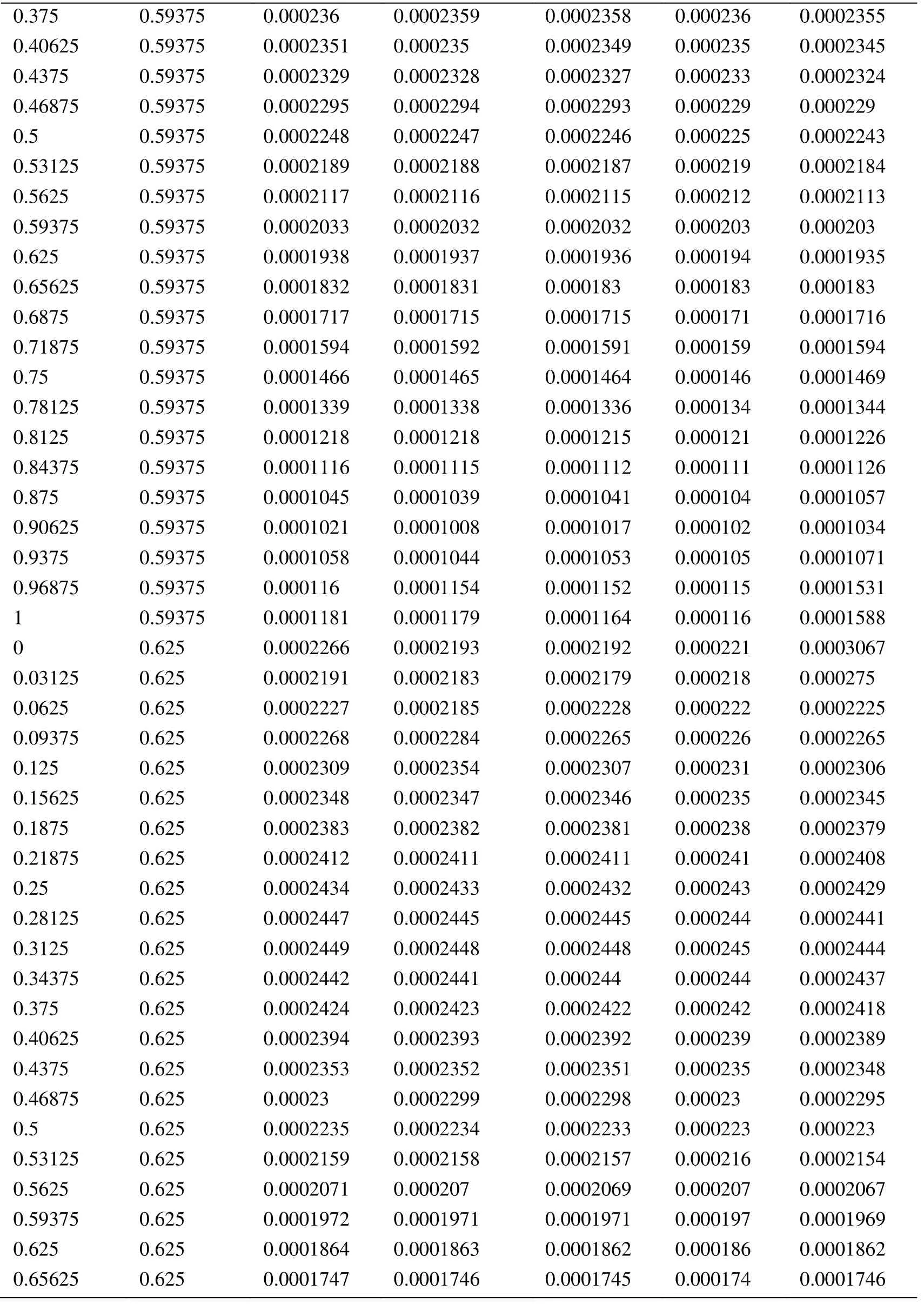
0.375 0.59375 0.000236 0.0002359 0.0002358 0.000236 0.0002355 0.40625 0.59375 0.0002351 0.000235 0.0002349 0.000235 0.0002345 0.4375 0.59375 0.0002329 0.0002328 0.0002327 0.000233 0.0002324 0.46875 0.59375 0.0002295 0.0002294 0.0002293 0.000229 0.000229 0.5 0.59375 0.0002248 0.0002247 0.0002246 0.000225 0.0002243 0.53125 0.59375 0.0002189 0.0002188 0.0002187 0.000219 0.0002184 0.5625 0.59375 0.0002117 0.0002116 0.0002115 0.000212 0.0002113 0.59375 0.59375 0.0002033 0.0002032 0.0002032 0.000203 0.000203 0.625 0.59375 0.0001938 0.0001937 0.0001936 0.000194 0.0001935 0.65625 0.59375 0.0001832 0.0001831 0.000183 0.000183 0.000183 0.6875 0.59375 0.0001717 0.0001715 0.0001715 0.000171 0.0001716 0.71875 0.59375 0.0001594 0.0001592 0.0001591 0.000159 0.0001594 0.75 0.59375 0.0001466 0.0001465 0.0001464 0.000146 0.0001469 0.78125 0.59375 0.0001339 0.0001338 0.0001336 0.000134 0.0001344 0.8125 0.59375 0.0001218 0.0001218 0.0001215 0.000121 0.0001226 0.84375 0.59375 0.0001116 0.0001115 0.0001112 0.000111 0.0001126 0.875 0.59375 0.0001045 0.0001039 0.0001041 0.000104 0.0001057 0.90625 0.59375 0.0001021 0.0001008 0.0001017 0.000102 0.0001034 0.9375 0.59375 0.0001058 0.0001044 0.0001053 0.000105 0.0001071 0.96875 0.59375 0.000116 0.0001154 0.0001152 0.000115 0.0001531 1 0.59375 0.0001181 0.0001179 0.0001164 0.000116 0.0001588 0 0.625 0.0002266 0.0002193 0.0002192 0.000221 0.0003067 0.03125 0.625 0.0002191 0.0002183 0.0002179 0.000218 0.000275 0.0625 0.625 0.0002227 0.0002185 0.0002228 0.000222 0.0002225 0.09375 0.625 0.0002268 0.0002284 0.0002265 0.000226 0.0002265 0.125 0.625 0.0002309 0.0002354 0.0002307 0.000231 0.0002306 0.15625 0.625 0.0002348 0.0002347 0.0002346 0.000235 0.0002345 0.1875 0.625 0.0002383 0.0002382 0.0002381 0.000238 0.0002379 0.21875 0.625 0.0002412 0.0002411 0.0002411 0.000241 0.0002408 0.25 0.625 0.0002434 0.0002433 0.0002432 0.000243 0.0002429 0.28125 0.625 0.0002447 0.0002445 0.0002445 0.000244 0.0002441 0.3125 0.625 0.0002449 0.0002448 0.0002448 0.000245 0.0002444 0.34375 0.625 0.0002442 0.0002441 0.000244 0.000244 0.0002437 0.375 0.625 0.0002424 0.0002423 0.0002422 0.000242 0.0002418 0.40625 0.625 0.0002394 0.0002393 0.0002392 0.000239 0.0002389 0.4375 0.625 0.0002353 0.0002352 0.0002351 0.000235 0.0002348 0.46875 0.625 0.00023 0.0002299 0.0002298 0.00023 0.0002295 0.5 0.625 0.0002235 0.0002234 0.0002233 0.000223 0.000223 0.53125 0.625 0.0002159 0.0002158 0.0002157 0.000216 0.0002154 0.5625 0.625 0.0002071 0.000207 0.0002069 0.000207 0.0002067 0.59375 0.625 0.0001972 0.0001971 0.0001971 0.000197 0.0001969 0.625 0.625 0.0001864 0.0001863 0.0001862 0.000186 0.0001862 0.65625 0.625 0.0001747 0.0001746 0.0001745 0.000174 0.0001746

0.6875 0.625 0.0001624 0.0001622 0.0001621 0.000162 0.0001624 0.71875 0.625 0.0001497 0.0001495 0.0001495 0.000149 0.0001499 0.75 0.625 0.0001372 0.000137 0.0001369 0.000137 0.0001377 0.78125 0.625 0.0001255 0.0001255 0.0001252 0.000125 0.0001263 0.8125 0.625 0.0001158 0.0001158 0.0001155 0.000115 0.0001168 0.84375 0.625 0.0001094 0.0001093 0.000109 0.000109 0.0001106 0.875 0.625 0.0001077 0.0001072 0.0001073 0.000107 0.000109 0.90625 0.625 0.0001119 0.0001108 0.0001115 0.000112 0.0001132 0.9375 0.625 0.0001224 0.0001212 0.0001218 0.000122 0.0001236 0.96875 0.625 0.0001387 0.0001383 0.0001381 0.000137 0.0001914 1 0.625 0.0001423 0.0001432 0.0001424 0.000141 0.0002083 0 0.65625 0.0002601 0.0002529 0.000253 0.000254 0.0003623 0.03125 0.65625 0.0002512 0.0002505 0.0002502 0.000251 0.0003218 0.0625 0.65625 0.0002527 0.0002489 0.0002528 0.000252 0.0002524 0.09375 0.65625 0.0002545 0.000256 0.0002542 0.000254 0.0002541 0.125 0.65625 0.0002562 0.0002602 0.0002559 0.000256 0.0002558 0.15625 0.65625 0.0002576 0.0002574 0.0002574 0.000257 0.0002572 0.1875 0.65625 0.0002586 0.0002585 0.0002584 0.000258 0.0002581 0.21875 0.65625 0.000259 0.0002589 0.0002588 0.000259 0.0002585 0.25 0.65625 0.0002587 0.0002586 0.0002585 0.000259 0.0002582 0.28125 0.65625 0.0002576 0.0002575 0.0002574 0.000257 0.0002571 0.3125 0.65625 0.0002556 0.0002555 0.0002554 0.000255 0.0002551 0.34375 0.65625 0.0002526 0.0002525 0.0002524 0.000252 0.0002521 0.375 0.65625 0.0002486 0.0002485 0.0002484 0.000248 0.0002481 0.40625 0.65625 0.0002435 0.0002434 0.0002434 0.000243 0.000243 0.4375 0.65625 0.0002374 0.0002373 0.0002372 0.000237 0.0002369 0.46875 0.65625 0.0002302 0.0002301 0.00023 0.00023 0.0002297 0.5 0.65625 0.0002219 0.0002218 0.0002217 0.000222 0.0002214 0.53125 0.65625 0.0002125 0.0002124 0.0002124 0.000212 0.0002121 0.5625 0.65625 0.0002022 0.0002021 0.000202 0.000202 0.0002019 0.59375 0.65625 0.000191 0.0001909 0.0001908 0.000191 0.0001908 0.625 0.65625 0.000179 0.0001789 0.0001788 0.000179 0.0001789 0.65625 0.65625 0.0001665 0.0001664 0.0001663 0.000166 0.0001666 0.6875 0.65625 0.0001538 0.0001537 0.0001536 0.000154 0.0001541 0.71875 0.65625 0.0001415 0.0001413 0.0001412 0.000141 0.0001419 0.75 0.65625 0.0001301 0.00013 0.0001299 0.00013 0.0001309 0.78125 0.65625 0.0001209 0.0001208 0.0001206 0.000121 0.0001219 0.8125 0.65625 0.0001151 0.0001151 0.0001148 0.000115 0.0001163 0.84375 0.65625 0.000114 0.0001139 0.0001137 0.000114 0.0001154 0.875 0.65625 0.0001187 0.0001183 0.0001184 0.000118 0.0001201 0.90625 0.65625 0.0001294 0.0001286 0.0001291 0.000129 0.0001308 0.9375 0.65625 0.0001459 0.0001451 0.0001454 0.000146 0.0001472 0.96875 0.65625 0.0001673 0.000167 0.0001669 0.000166 0.0002355

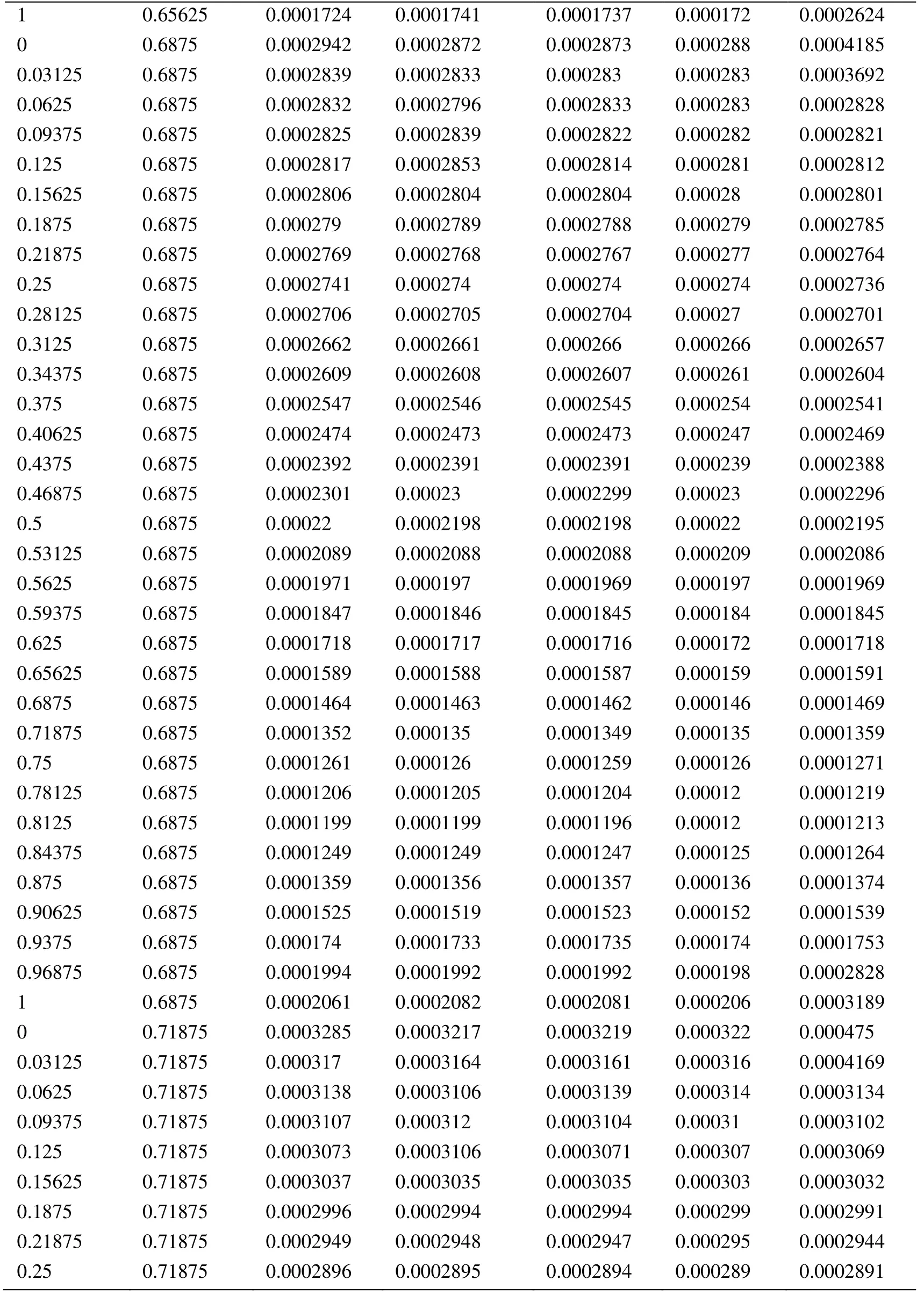
1 0.65625 0.0001724 0.0001741 0.0001737 0.000172 0.0002624 0 0.6875 0.0002942 0.0002872 0.0002873 0.000288 0.0004185 0.03125 0.6875 0.0002839 0.0002833 0.000283 0.000283 0.0003692 0.0625 0.6875 0.0002832 0.0002796 0.0002833 0.000283 0.0002828 0.09375 0.6875 0.0002825 0.0002839 0.0002822 0.000282 0.0002821 0.125 0.6875 0.0002817 0.0002853 0.0002814 0.000281 0.0002812 0.15625 0.6875 0.0002806 0.0002804 0.0002804 0.00028 0.0002801 0.1875 0.6875 0.000279 0.0002789 0.0002788 0.000279 0.0002785 0.21875 0.6875 0.0002769 0.0002768 0.0002767 0.000277 0.0002764 0.25 0.6875 0.0002741 0.000274 0.000274 0.000274 0.0002736 0.28125 0.6875 0.0002706 0.0002705 0.0002704 0.00027 0.0002701 0.3125 0.6875 0.0002662 0.0002661 0.000266 0.000266 0.0002657 0.34375 0.6875 0.0002609 0.0002608 0.0002607 0.000261 0.0002604 0.375 0.6875 0.0002547 0.0002546 0.0002545 0.000254 0.0002541 0.40625 0.6875 0.0002474 0.0002473 0.0002473 0.000247 0.0002469 0.4375 0.6875 0.0002392 0.0002391 0.0002391 0.000239 0.0002388 0.46875 0.6875 0.0002301 0.00023 0.0002299 0.00023 0.0002296 0.5 0.6875 0.00022 0.0002198 0.0002198 0.00022 0.0002195 0.53125 0.6875 0.0002089 0.0002088 0.0002088 0.000209 0.0002086 0.5625 0.6875 0.0001971 0.000197 0.0001969 0.000197 0.0001969 0.59375 0.6875 0.0001847 0.0001846 0.0001845 0.000184 0.0001845 0.625 0.6875 0.0001718 0.0001717 0.0001716 0.000172 0.0001718 0.65625 0.6875 0.0001589 0.0001588 0.0001587 0.000159 0.0001591 0.6875 0.6875 0.0001464 0.0001463 0.0001462 0.000146 0.0001469 0.71875 0.6875 0.0001352 0.000135 0.0001349 0.000135 0.0001359 0.75 0.6875 0.0001261 0.000126 0.0001259 0.000126 0.0001271 0.78125 0.6875 0.0001206 0.0001205 0.0001204 0.00012 0.0001219 0.8125 0.6875 0.0001199 0.0001199 0.0001196 0.00012 0.0001213 0.84375 0.6875 0.0001249 0.0001249 0.0001247 0.000125 0.0001264 0.875 0.6875 0.0001359 0.0001356 0.0001357 0.000136 0.0001374 0.90625 0.6875 0.0001525 0.0001519 0.0001523 0.000152 0.0001539 0.9375 0.6875 0.000174 0.0001733 0.0001735 0.000174 0.0001753 0.96875 0.6875 0.0001994 0.0001992 0.0001992 0.000198 0.0002828 1 0.6875 0.0002061 0.0002082 0.0002081 0.000206 0.0003189 0 0.71875 0.0003285 0.0003217 0.0003219 0.000322 0.000475 0.03125 0.71875 0.000317 0.0003164 0.0003161 0.000316 0.0004169 0.0625 0.71875 0.0003138 0.0003106 0.0003139 0.000314 0.0003134 0.09375 0.71875 0.0003107 0.000312 0.0003104 0.00031 0.0003102 0.125 0.71875 0.0003073 0.0003106 0.0003071 0.000307 0.0003069 0.15625 0.71875 0.0003037 0.0003035 0.0003035 0.000303 0.0003032 0.1875 0.71875 0.0002996 0.0002994 0.0002994 0.000299 0.0002991 0.21875 0.71875 0.0002949 0.0002948 0.0002947 0.000295 0.0002944 0.25 0.71875 0.0002896 0.0002895 0.0002894 0.000289 0.0002891

0.28125 0.71875 0.0002836 0.0002835 0.0002834 0.000283 0.000283 0.3125 0.71875 0.0002767 0.0002766 0.0002766 0.000277 0.0002762 0.34375 0.71875 0.0002691 0.000269 0.0002689 0.000269 0.0002686 0.375 0.71875 0.0002606 0.0002605 0.0002604 0.00026 0.0002601 0.40625 0.71875 0.0002512 0.0002511 0.000251 0.000251 0.0002507 0.4375 0.71875 0.0002409 0.0002408 0.0002407 0.000241 0.0002404 0.46875 0.71875 0.0002297 0.0002296 0.0002295 0.00023 0.0002293 0.5 0.71875 0.0002178 0.0002177 0.0002176 0.000218 0.0002174 0.53125 0.71875 0.0002051 0.000205 0.0002049 0.000205 0.0002048 0.5625 0.71875 0.0001919 0.0001918 0.0001917 0.000192 0.0001918 0.59375 0.71875 0.0001784 0.0001783 0.0001782 0.000178 0.0001784 0.625 0.71875 0.0001649 0.0001648 0.0001647 0.000165 0.0001651 0.65625 0.71875 0.000152 0.0001519 0.0001518 0.000152 0.0001524 0.6875 0.71875 0.0001404 0.0001403 0.0001402 0.00014 0.0001411 0.71875 0.71875 0.0001312 0.000131 0.000131 0.000131 0.0001322 0.75 0.71875 0.0001256 0.0001254 0.0001253 0.000125 0.0001269 0.78125 0.71875 0.0001249 0.0001248 0.0001246 0.000125 0.0001263 0.8125 0.71875 0.00013 0.0001299 0.0001297 0.00013 0.0001315 0.84375 0.71875 0.000141 0.000141 0.0001408 0.000141 0.0001425 0.875 0.71875 0.0001577 0.0001575 0.0001575 0.000158 0.0001592 0.90625 0.71875 0.0001793 0.0001788 0.0001791 0.000179 0.0001807 0.9375 0.71875 0.0002049 0.0002044 0.0002044 0.000205 0.0002062 0.96875 0.71875 0.0002339 0.0002337 0.0002337 0.000233 0.0003323 1 0.71875 0.0002419 0.0002443 0.0002445 0.000242 0.0003767 0 0.75 0.0003631 0.0003544 0.0003566 0.000357 0.0005317 0.03125 0.75 0.0003502 0.0003488 0.0003494 0.00035 0.0004648 0.0625 0.75 0.0003446 0.0003405 0.0003447 0.000344 0.0003442 0.09375 0.75 0.000339 0.0003419 0.0003388 0.000339 0.0003385 0.125 0.75 0.0003331 0.000338 0.0003329 0.000333 0.0003326 0.15625 0.75 0.0003268 0.0003278 0.0003267 0.000327 0.0003263 0.1875 0.75 0.0003202 0.0003205 0.00032 0.00032 0.0003197 0.21875 0.75 0.0003129 0.0003129 0.0003128 0.000313 0.0003124 0.25 0.75 0.0003051 0.0003051 0.0003049 0.000305 0.0003046 0.28125 0.75 0.0002966 0.0002965 0.0002964 0.000296 0.000296 0.3125 0.75 0.0002873 0.0002873 0.0002871 0.000287 0.0002868 0.34375 0.75 0.0002772 0.0002772 0.0002771 0.000277 0.0002767 0.375 0.75 0.0002664 0.0002664 0.0002662 0.000266 0.0002659 0.40625 0.75 0.0002547 0.0002547 0.0002546 0.000255 0.0002543 0.4375 0.75 0.0002423 0.0002423 0.0002421 0.000242 0.0002419 0.46875 0.75 0.0002292 0.0002292 0.000229 0.000229 0.0002288 0.5 0.75 0.0002154 0.0002154 0.0002152 0.000215 0.0002151 0.53125 0.75 0.0002012 0.0002012 0.000201 0.000201 0.000201 0.5625 0.75 0.0001867 0.0001867 0.0001865 0.000186 0.0001866

0.59375 0.75 0.0001723 0.0001723 0.0001721 0.000172 0.0001724 0.625 0.75 0.0001586 0.0001585 0.0001583 0.000158 0.0001589 0.65625 0.75 0.0001462 0.0001461 0.0001459 0.000146 0.0001468 0.6875 0.75 0.0001363 0.0001362 0.000136 0.000136 0.0001371 0.71875 0.75 0.00013 0.0001299 0.0001298 0.00013 0.0001312 0.75 0.75 0.0001288 0.0001287 0.0001286 0.000129 0.0001303 0.78125 0.75 0.0001335 0.0001334 0.0001333 0.000133 0.0001351 0.8125 0.75 0.0001444 0.0001443 0.0001442 0.000144 0.000146 0.84375 0.75 0.000161 0.0001609 0.0001608 0.000161 0.0001626 0.875 0.75 0.0001827 0.0001824 0.0001825 0.000183 0.0001841 0.90625 0.75 0.0002085 0.000208 0.0002083 0.000208 0.0002099 0.9375 0.75 0.0002377 0.0002373 0.0002372 0.000238 0.0002391 0.96875 0.75 0.0002699 0.0002699 0.0002698 0.000269 0.0003831 1 0.75 0.0002793 0.0002818 0.0002822 0.000279 0.0004355 0 0.78125 0.0003977 0.0003893 0.0003914 0.000391 0.0005885 0.03125 0.78125 0.0003835 0.0003828 0.0003827 0.000383 0.0005127 0.0625 0.78125 0.0003755 0.0003735 0.0003756 0.000375 0.000375 0.09375 0.78125 0.0003673 0.0003693 0.0003671 0.000367 0.0003668 0.125 0.78125 0.0003589 0.0003637 0.0003587 0.000359 0.0003584 0.15625 0.78125 0.0003501 0.0003513 0.0003499 0.00035 0.0003496 0.1875 0.78125 0.0003408 0.000341 0.0003406 0.000341 0.0003403 0.21875 0.78125 0.000331 0.0003309 0.0003308 0.000331 0.0003305 0.25 0.78125 0.0003206 0.0003207 0.0003204 0.00032 0.0003201 0.28125 0.78125 0.0003095 0.0003097 0.0003094 0.000309 0.000309 0.3125 0.78125 0.0002978 0.000298 0.0002976 0.000298 0.0002973 0.34375 0.78125 0.0002853 0.0002855 0.0002851 0.000285 0.0002848 0.375 0.78125 0.0002721 0.0002723 0.0002719 0.000272 0.0002716 0.40625 0.78125 0.0002582 0.0002584 0.000258 0.000258 0.0002578 0.4375 0.78125 0.0002436 0.0002439 0.0002435 0.000243 0.0002432 0.46875 0.78125 0.0002285 0.0002287 0.0002283 0.000228 0.0002282 0.5 0.78125 0.000213 0.0002132 0.0002127 0.000213 0.0002127 0.53125 0.78125 0.0001972 0.0001974 0.000197 0.000197 0.000197 0.5625 0.78125 0.0001815 0.0001818 0.0001813 0.000181 0.0001815 0.59375 0.78125 0.0001665 0.0001668 0.0001663 0.000166 0.0001667 0.625 0.78125 0.0001529 0.0001531 0.0001526 0.000153 0.0001534 0.65625 0.78125 0.0001417 0.0001419 0.0001414 0.000141 0.0001425 0.6875 0.78125 0.0001342 0.0001344 0.0001339 0.000134 0.0001354 0.71875 0.78125 0.0001319 0.000132 0.0001316 0.000132 0.0001333 0.75 0.78125 0.0001357 0.0001358 0.0001354 0.000135 0.0001373 0.78125 0.78125 0.000146 0.000146 0.0001457 0.000146 0.0001476 0.8125 0.78125 0.0001623 0.0001624 0.0001621 0.000162 0.0001639 0.84375 0.78125 0.0001839 0.0001839 0.0001838 0.000184 0.0001855 0.875 0.78125 0.0002099 0.0002098 0.0002097 0.00021 0.0002114

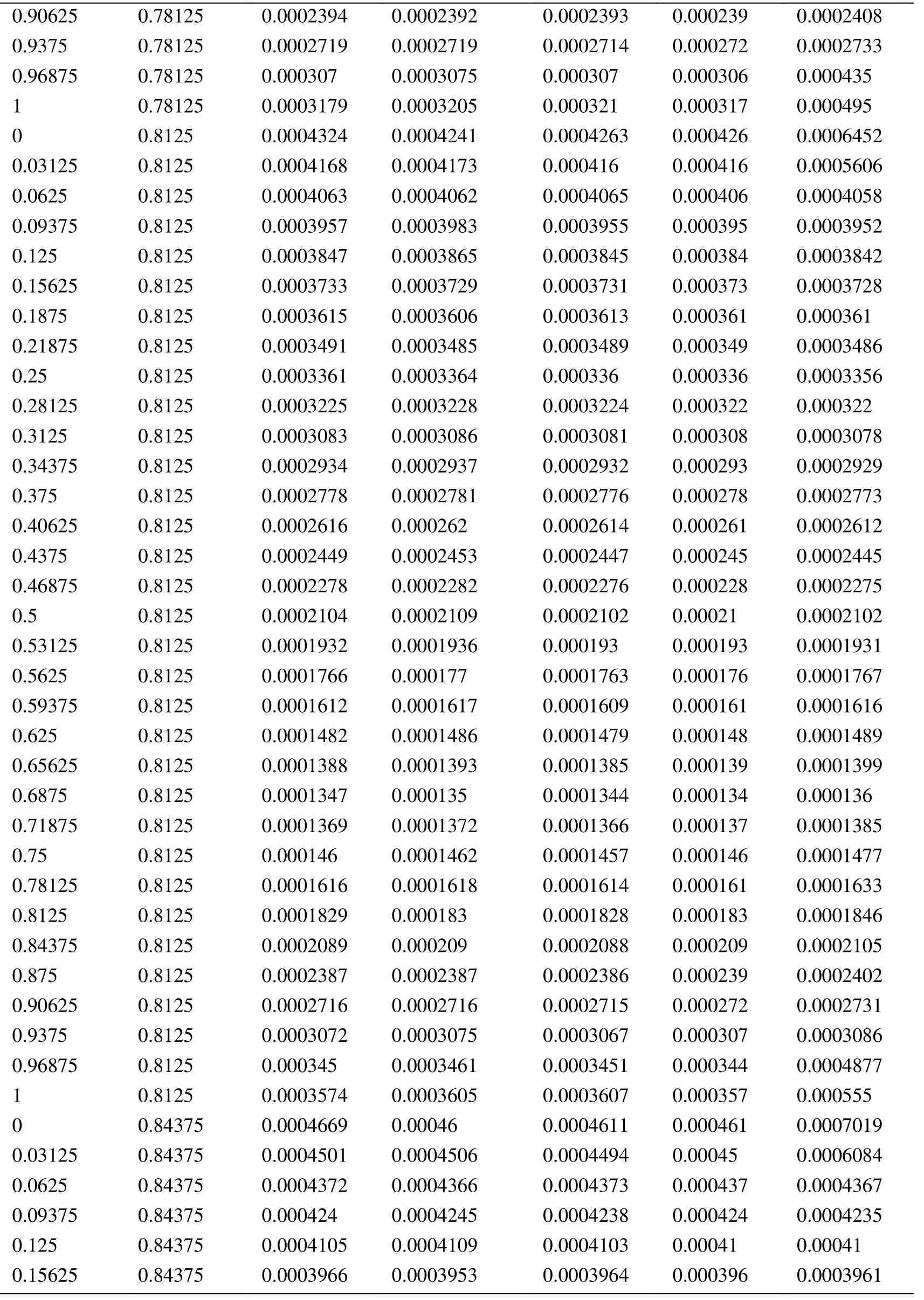
0.90625 0.78125 0.0002394 0.0002392 0.0002393 0.000239 0.0002408 0.9375 0.78125 0.0002719 0.0002719 0.0002714 0.000272 0.0002733 0.96875 0.78125 0.000307 0.0003075 0.000307 0.000306 0.000435 1 0.78125 0.0003179 0.0003205 0.000321 0.000317 0.000495 0 0.8125 0.0004324 0.0004241 0.0004263 0.000426 0.0006452 0.03125 0.8125 0.0004168 0.0004173 0.000416 0.000416 0.0005606 0.0625 0.8125 0.0004063 0.0004062 0.0004065 0.000406 0.0004058 0.09375 0.8125 0.0003957 0.0003983 0.0003955 0.000395 0.0003952 0.125 0.8125 0.0003847 0.0003865 0.0003845 0.000384 0.0003842 0.15625 0.8125 0.0003733 0.0003729 0.0003731 0.000373 0.0003728 0.1875 0.8125 0.0003615 0.0003606 0.0003613 0.000361 0.000361 0.21875 0.8125 0.0003491 0.0003485 0.0003489 0.000349 0.0003486 0.25 0.8125 0.0003361 0.0003364 0.000336 0.000336 0.0003356 0.28125 0.8125 0.0003225 0.0003228 0.0003224 0.000322 0.000322 0.3125 0.8125 0.0003083 0.0003086 0.0003081 0.000308 0.0003078 0.34375 0.8125 0.0002934 0.0002937 0.0002932 0.000293 0.0002929 0.375 0.8125 0.0002778 0.0002781 0.0002776 0.000278 0.0002773 0.40625 0.8125 0.0002616 0.000262 0.0002614 0.000261 0.0002612 0.4375 0.8125 0.0002449 0.0002453 0.0002447 0.000245 0.0002445 0.46875 0.8125 0.0002278 0.0002282 0.0002276 0.000228 0.0002275 0.5 0.8125 0.0002104 0.0002109 0.0002102 0.00021 0.0002102 0.53125 0.8125 0.0001932 0.0001936 0.000193 0.000193 0.0001931 0.5625 0.8125 0.0001766 0.000177 0.0001763 0.000176 0.0001767 0.59375 0.8125 0.0001612 0.0001617 0.0001609 0.000161 0.0001616 0.625 0.8125 0.0001482 0.0001486 0.0001479 0.000148 0.0001489 0.65625 0.8125 0.0001388 0.0001393 0.0001385 0.000139 0.0001399 0.6875 0.8125 0.0001347 0.000135 0.0001344 0.000134 0.000136 0.71875 0.8125 0.0001369 0.0001372 0.0001366 0.000137 0.0001385 0.75 0.8125 0.000146 0.0001462 0.0001457 0.000146 0.0001477 0.78125 0.8125 0.0001616 0.0001618 0.0001614 0.000161 0.0001633 0.8125 0.8125 0.0001829 0.000183 0.0001828 0.000183 0.0001846 0.84375 0.8125 0.0002089 0.000209 0.0002088 0.000209 0.0002105 0.875 0.8125 0.0002387 0.0002387 0.0002386 0.000239 0.0002402 0.90625 0.8125 0.0002716 0.0002716 0.0002715 0.000272 0.0002731 0.9375 0.8125 0.0003072 0.0003075 0.0003067 0.000307 0.0003086 0.96875 0.8125 0.000345 0.0003461 0.0003451 0.000344 0.0004877 1 0.8125 0.0003574 0.0003605 0.0003607 0.000357 0.000555 0 0.84375 0.0004669 0.00046 0.0004611 0.000461 0.0007019 0.03125 0.84375 0.0004501 0.0004506 0.0004494 0.00045 0.0006084 0.0625 0.84375 0.0004372 0.0004366 0.0004373 0.000437 0.0004367 0.09375 0.84375 0.000424 0.0004245 0.0004238 0.000424 0.0004235 0.125 0.84375 0.0004105 0.0004109 0.0004103 0.00041 0.00041 0.15625 0.84375 0.0003966 0.0003953 0.0003964 0.000396 0.0003961

0.1875 0.84375 0.0003822 0.0003807 0.000382 0.000382 0.0003817 0.21875 0.84375 0.0003672 0.0003663 0.0003671 0.000367 0.0003667 0.25 0.84375 0.0003517 0.000352 0.0003516 0.000352 0.0003512 0.28125 0.84375 0.0003356 0.0003357 0.0003354 0.000335 0.0003351 0.3125 0.84375 0.0003188 0.000319 0.0003187 0.000319 0.0003183 0.34375 0.84375 0.0003015 0.0003016 0.0003013 0.000301 0.000301 0.375 0.84375 0.0002835 0.0002837 0.0002833 0.000283 0.0002831 0.40625 0.84375 0.000265 0.0002653 0.0002648 0.000265 0.0002646 0.4375 0.84375 0.0002462 0.0002464 0.000246 0.000246 0.0002458 0.46875 0.84375 0.0002271 0.0002273 0.0002268 0.000227 0.0002268 0.5 0.84375 0.000208 0.0002083 0.0002077 0.000208 0.0002078 0.53125 0.84375 0.0001894 0.0001897 0.0001891 0.000189 0.0001894 0.5625 0.84375 0.000172 0.0001723 0.0001717 0.000172 0.0001722 0.59375 0.84375 0.0001566 0.0001569 0.0001563 0.000156 0.0001571 0.625 0.84375 0.0001447 0.0001451 0.0001444 0.000144 0.0001456 0.65625 0.84375 0.000138 0.0001383 0.0001376 0.000138 0.0001392 0.6875 0.84375 0.0001377 0.0001381 0.0001374 0.000137 0.0001393 0.71875 0.84375 0.0001449 0.0001452 0.0001446 0.000145 0.0001466 0.75 0.84375 0.0001592 0.0001594 0.000159 0.000159 0.000161 0.78125 0.84375 0.0001799 0.00018 0.0001797 0.00018 0.0001816 0.8125 0.84375 0.0002057 0.0002057 0.0002055 0.000206 0.0002073 0.84375 0.84375 0.0002356 0.0002357 0.0002355 0.000236 0.0002372 0.875 0.84375 0.0002688 0.000269 0.0002687 0.000269 0.0002704 0.90625 0.84375 0.0003049 0.0003051 0.0003048 0.000305 0.0003063 0.9375 0.84375 0.0003433 0.0003439 0.0003429 0.000343 0.0003447 0.96875 0.84375 0.0003839 0.0003852 0.000384 0.000383 0.0005411 1 0.84375 0.0003976 0.0004019 0.000401 0.000396 0.0006155 0 0.875 0.0005014 0.0004952 0.0004958 0.000495 0.0007585 0.03125 0.875 0.0004833 0.0004827 0.0004826 0.000483 0.0006561 0.0625 0.875 0.000468 0.0004662 0.0004681 0.000468 0.0004674 0.09375 0.875 0.0004523 0.000451 0.0004521 0.000452 0.0004518 0.125 0.875 0.0004363 0.0004351 0.0004361 0.000436 0.0004358 0.15625 0.875 0.0004199 0.0004175 0.0004197 0.00042 0.0004194 0.1875 0.875 0.0004029 0.0004009 0.0004027 0.000403 0.0004024 0.21875 0.875 0.0003854 0.0003842 0.0003853 0.000385 0.0003849 0.25 0.875 0.0003673 0.0003672 0.0003672 0.000367 0.0003669 0.28125 0.875 0.0003487 0.0003481 0.0003485 0.000348 0.0003482 0.3125 0.875 0.0003294 0.0003288 0.0003293 0.000329 0.000329 0.34375 0.875 0.0003096 0.000309 0.0003094 0.000309 0.0003092 0.375 0.875 0.0002893 0.0002886 0.0002891 0.000289 0.0002889 0.40625 0.875 0.0002685 0.0002678 0.0002683 0.000268 0.0002681 0.4375 0.875 0.0002475 0.0002468 0.0002473 0.000247 0.0002472 0.46875 0.875 0.0002264 0.0002257 0.0002262 0.000226 0.0002262

0.09375 0.96875 0.0005373 0.000538 0.0005364 0.000534 0.000685 0.125 0.96875 0.0005139 0.000514 0.0005129 0.000511 0.000651 0.15625 0.96875 0.0004899 0.0004898 0.0004889 0.000487 0.0006164 0.1875 0.96875 0.0004654 0.0004657 0.0004643 0.000463 0.0005811 0.21875 0.96875 0.0004403 0.0004409 0.0004391 0.000438 0.0005452 0.25 0.96875 0.0004147 0.0004145 0.0004134 0.000412 0.0005087 0.28125 0.96875 0.0003885 0.0003877 0.0003871 0.000386 0.0004716 0.3125 0.96875 0.0003619 0.0003609 0.0003604 0.00036 0.000434 0.34375 0.96875 0.0003348 0.0003338 0.0003332 0.000333 0.000396 0.375 0.96875 0.0003074 0.0003064 0.0003057 0.000305 0.0003578 0.40625 0.96875 0.00028 0.0002789 0.0002781 0.000278 0.0003198 0.4375 0.96875 0.0002527 0.0002516 0.0002506 0.000251 0.0002823 0.46875 0.96875 0.0002262 0.0002251 0.0002239 0.000224 0.0002462 0.5 0.96875 0.0002012 0.0002001 0.0001988 0.000199 0.000213 0.53125 0.96875 0.0001789 0.0001779 0.0001763 0.000177 0.0001851 0.5625 0.96875 0.0001613 0.0001605 0.0001586 0.00016 0.0001663 0.59375 0.96875 0.0001505 0.00015 0.0001481 0.000149 0.0001607 0.625 0.96875 0.000149 0.0001486 0.0001468 0.000148 0.0001698 0.65625 0.96875 0.0001577 0.0001574 0.0001559 0.000156 0.000192 0.6875 0.96875 0.000176 0.0001758 0.0001747 0.000175 0.0002244 0.71875 0.96875 0.0002021 0.000202 0.0002012 0.000201 0.0002642 0.75 0.96875 0.0002342 0.0002342 0.0002336 0.000233 0.0003093 0.78125 0.96875 0.0002707 0.0002714 0.0002704 0.000269 0.0003583 0.8125 0.96875 0.0003107 0.0003122 0.0003106 0.000309 0.0004104 0.84375 0.96875 0.0003535 0.0003555 0.0003535 0.000352 0.0004651 0.875 0.96875 0.0003986 0.0004008 0.0003988 0.000397 0.0005219 0.90625 0.96875 0.0004458 0.0004468 0.0004461 0.000444 0.0005806 0.9375 0.96875 0.0004948 0.0004931 0.0004954 0.000493 0.0006411 0.96875 0.96875 0.0005457 0.0005406 0.0005432 0.000543 0.0007004 1 0.96875 0.000565 0.0005665 0.0005662 0.000563 0.0007936 0 1 0.0006225 0.0005992 0.0006273 0.0006 0.0010391 0.03125 1 0.0006073 0.0005831 0.0006018 0.000594 0.0010999 0.0625 1 0.000585 0.000557 0.0005744 0.000569 0.0007766 0.09375 1 0.0005614 0.0005414 0.0005495 0.000545 0.0007373 0.125 1 0.000537 0.0005219 0.0005248 0.000521 0.0006971 0.15625 1 0.0005119 0.000497 0.0004994 0.000496 0.0006563 0.1875 1 0.0004862 0.0004729 0.0004734 0.000471 0.0006151 0.21875 1 0.0004598 0.0004485 0.0004468 0.000445 0.0005734 0.25 1 0.0004329 0.000422 0.0004197 0.000418 0.0005314 0.28125 1 0.0004055 0.0003937 0.0003921 0.000391 0.0004892 0.3125 1 0.0003775 0.0003659 0.0003641 0.000364 0.0004467 0.34375 1 0.0003491 0.0003376 0.0003356 0.000336 0.0004042 0.375 1 0.0003204 0.0003092 0.0003068 0.000308 0.0003618

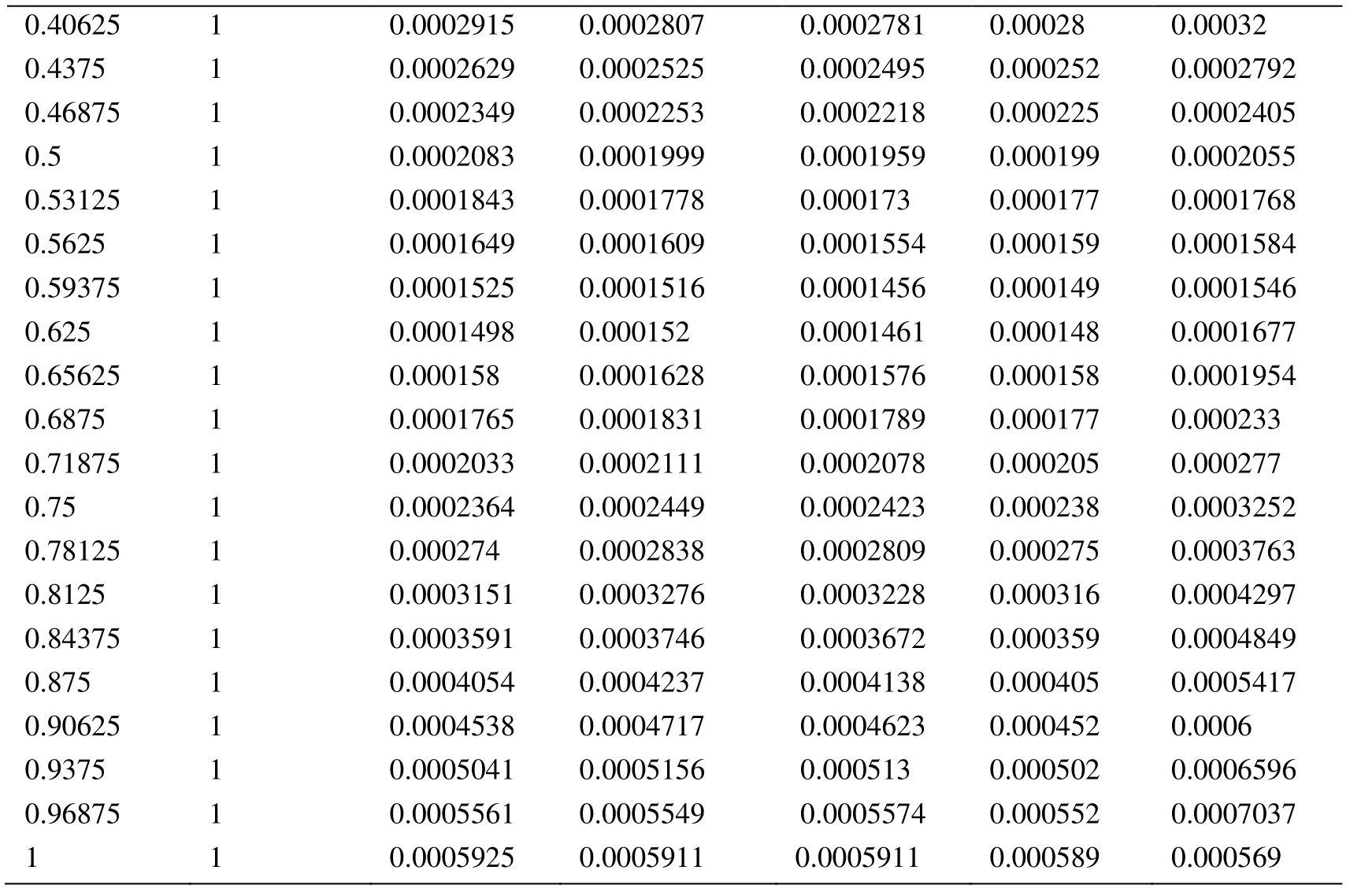
0.40625 1 0.0002915 0.0002807 0.0002781 0.00028 0.00032 0.4375 1 0.0002629 0.0002525 0.0002495 0.000252 0.0002792 0.46875 1 0.0002349 0.0002253 0.0002218 0.000225 0.0002405 0.5 1 0.0002083 0.0001999 0.0001959 0.000199 0.0002055 0.53125 1 0.0001843 0.0001778 0.000173 0.000177 0.0001768 0.5625 1 0.0001649 0.0001609 0.0001554 0.000159 0.0001584 0.59375 1 0.0001525 0.0001516 0.0001456 0.000149 0.0001546 0.625 1 0.0001498 0.000152 0.0001461 0.000148 0.0001677 0.65625 1 0.000158 0.0001628 0.0001576 0.000158 0.0001954 0.6875 1 0.0001765 0.0001831 0.0001789 0.000177 0.000233 0.71875 1 0.0002033 0.0002111 0.0002078 0.000205 0.000277 0.75 1 0.0002364 0.0002449 0.0002423 0.000238 0.0003252 0.78125 1 0.000274 0.0002838 0.0002809 0.000275 0.0003763 0.8125 1 0.0003151 0.0003276 0.0003228 0.000316 0.0004297 0.84375 1 0.0003591 0.0003746 0.0003672 0.000359 0.0004849 0.875 1 0.0004054 0.0004237 0.0004138 0.000405 0.0005417 0.90625 1 0.0004538 0.0004717 0.0004623 0.000452 0.0006 0.9375 1 0.0005041 0.0005156 0.000513 0.000502 0.0006596 0.96875 1 0.0005561 0.0005549 0.0005574 0.000552 0.0007037 1 1 0.0005925 0.0005911 0.0005911 0.000589 0.000569

Appendix B.Element Effectivity

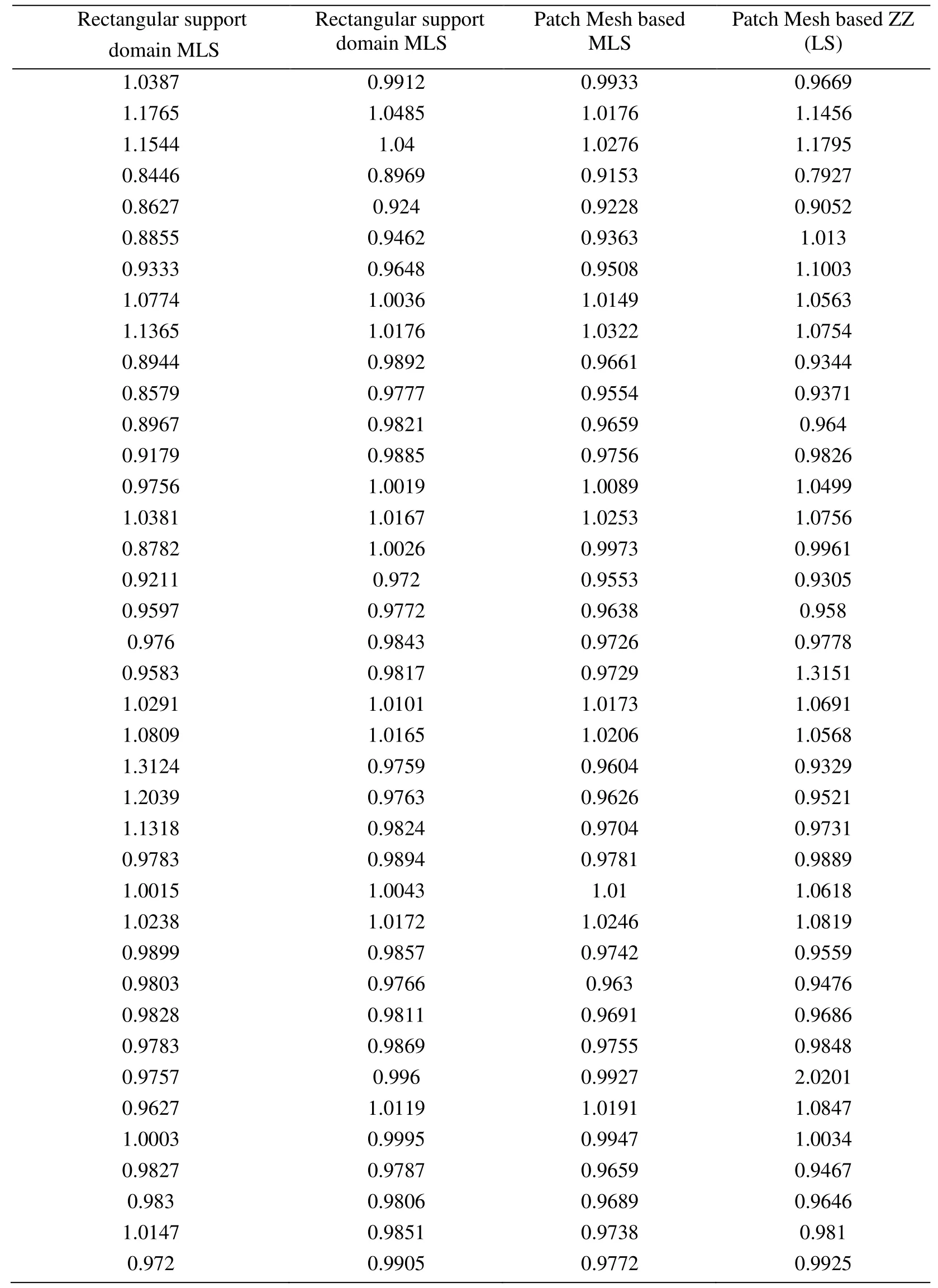
Rectangular support domain MLS Rectangular support domain MLS Patch Mesh based MLS Patch Mesh based ZZ (LS) 1.0387 0.9912 0.9933 0.9669 1.1765 1.0485 1.0176 1.1456 1.1544 1.04 1.0276 1.1795 0.8446 0.8969 0.9153 0.7927 0.8627 0.924 0.9228 0.9052 0.8855 0.9462 0.9363 1.013 0.9333 0.9648 0.9508 1.1003 1.0774 1.0036 1.0149 1.0563 1.1365 1.0176 1.0322 1.0754 0.8944 0.9892 0.9661 0.9344 0.8579 0.9777 0.9554 0.9371 0.8967 0.9821 0.9659 0.964 0.9179 0.9885 0.9756 0.9826 0.9756 1.0019 1.0089 1.0499 1.0381 1.0167 1.0253 1.0756 0.8782 1.0026 0.9973 0.9961 0.9211 0.972 0.9553 0.9305 0.9597 0.9772 0.9638 0.958 0.976 0.9843 0.9726 0.9778 0.9583 0.9817 0.9729 1.3151 1.0291 1.0101 1.0173 1.0691 1.0809 1.0165 1.0206 1.0568 1.3124 0.9759 0.9604 0.9329 1.2039 0.9763 0.9626 0.9521 1.1318 0.9824 0.9704 0.9731 0.9783 0.9894 0.9781 0.9889 1.0015 1.0043 1.01 1.0618 1.0238 1.0172 1.0246 1.0819 0.9899 0.9857 0.9742 0.9559 0.9803 0.9766 0.963 0.9476 0.9828 0.9811 0.9691 0.9686 0.9783 0.9869 0.9755 0.9848 0.9757 0.996 0.9927 2.0201 0.9627 1.0119 1.0191 1.0847 1.0003 0.9995 0.9947 1.0034 0.9827 0.9787 0.9659 0.9467 0.983 0.9806 0.9689 0.9646 1.0147 0.9851 0.9738 0.981 0.972 0.9905 0.9772 0.9925

0.9056 1.0055 1.0115 1.0795 1.0059 1.0097 1.0111 1.0551 0.9869 0.9832 0.9723 0.9532 0.9841 0.9812 0.9701 0.9618 0.9855 0.9841 0.9732 0.9777 1.0458 0.9874 0.976 0.9902 0.9791 0.9966 1.004 1.0722 0.9901 1.0116 1.0161 1.088 0.9922 0.9901 0.9819 0.9708 0.9861 0.983 0.973 0.961 0.9861 0.9841 0.9739 0.975 1.0177 0.9864 0.9754 0.9876 0.9982 0.9679 0.9607 1.2608 0.9985 1.0073 1.0124 1.1006 0.9971 0.9982 0.9933 1.0014 0.9889 0.9861 0.9775 0.9632 0.9874 0.9851 0.976 0.9735 0.9879 0.9861 0.9759 0.9854 0.9769 0.9857 0.9739 0.9937 1.0135 1.0005 1.0051 1.101 0.9996 1.0051 1.0035 1.0421 0.9921 0.9901 0.9832 0.9691 0.9894 0.987 0.9793 0.9732 0.9883 0.9867 0.9777 0.9839 0.9918 0.9859 0.9749 0.9928 0.9726 0.9865 0.9787 2.0093 0.9981 1.0082 1.0095 1.0859 0.9953 0.995 0.9898 0.9794 0.9917 0.9896 0.9834 0.9743 0.99 0.9881 0.9807 0.9832 0.9904 0.9866 0.977 0.992 0.9573 0.9846 0.9683 0.995 1.1133 1.0062 1.0097 1.1232 0.9981 1.0003 0.997 0.9951 0.9942 0.9928 0.988 0.9768 0.9921 0.9902 0.9844 0.9834 0.9897 0.9881 0.9802 0.9917 0.9845 0.9829 0.9714 0.9963 0.9877 0.9958 1.0057 1.1449 1.0008 1.0062 1.0052 1.0183 0.9968 0.9964 0.9931 0.9805 0.9944 0.9928 0.9886 0.9844 0.992 0.9903 0.9843 0.9918

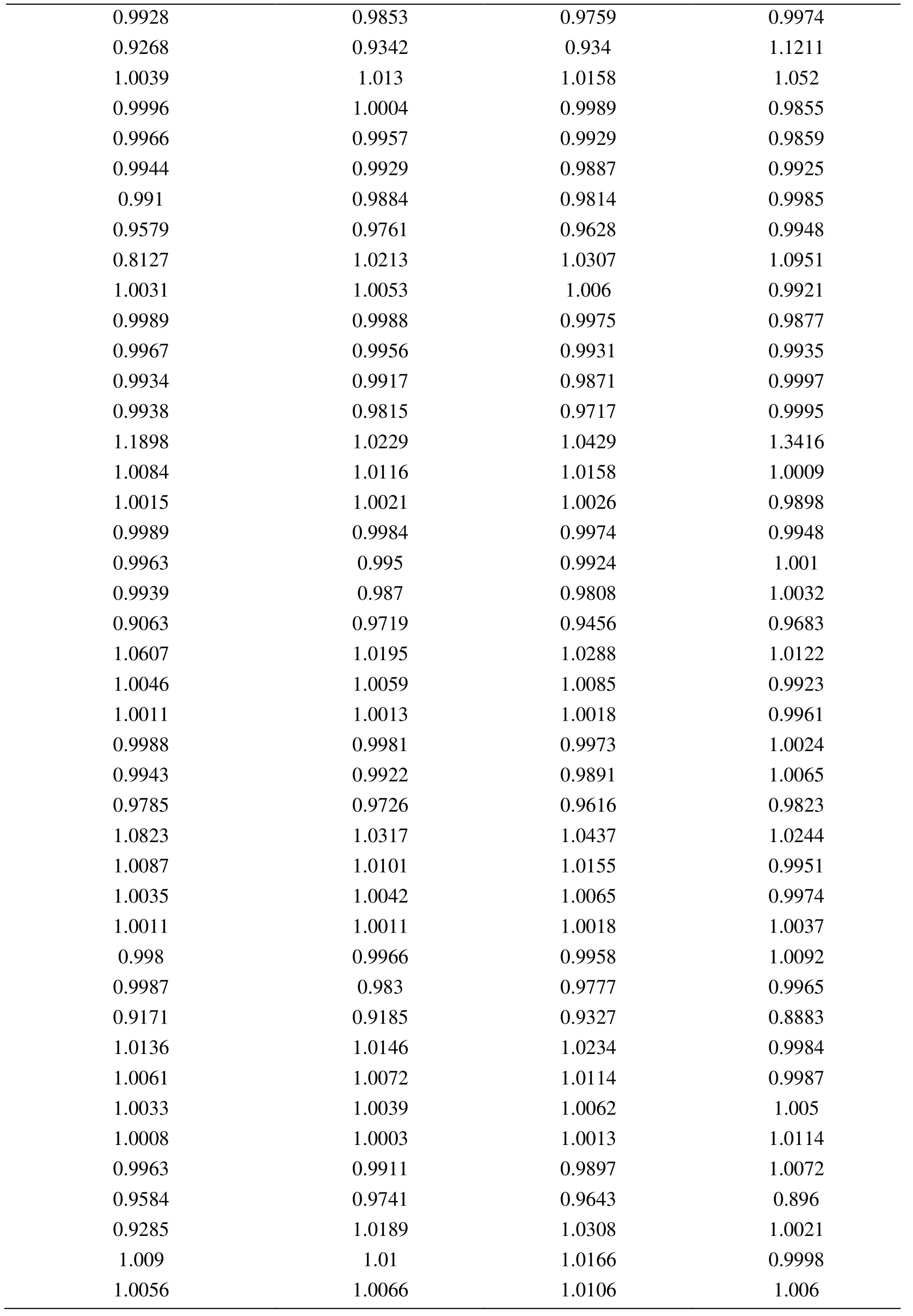
0.9928 0.9853 0.9759 0.9974 0.9268 0.9342 0.934 1.1211 1.0039 1.013 1.0158 1.052 0.9996 1.0004 0.9989 0.9855 0.9966 0.9957 0.9929 0.9859 0.9944 0.9929 0.9887 0.9925 0.991 0.9884 0.9814 0.9985 0.9579 0.9761 0.9628 0.9948 0.8127 1.0213 1.0307 1.0951 1.0031 1.0053 1.006 0.9921 0.9989 0.9988 0.9975 0.9877 0.9967 0.9956 0.9931 0.9935 0.9934 0.9917 0.9871 0.9997 0.9938 0.9815 0.9717 0.9995 1.1898 1.0229 1.0429 1.3416 1.0084 1.0116 1.0158 1.0009 1.0015 1.0021 1.0026 0.9898 0.9989 0.9984 0.9974 0.9948 0.9963 0.995 0.9924 1.001 0.9939 0.987 0.9808 1.0032 0.9063 0.9719 0.9456 0.9683 1.0607 1.0195 1.0288 1.0122 1.0046 1.0059 1.0085 0.9923 1.0011 1.0013 1.0018 0.9961 0.9988 0.9981 0.9973 1.0024 0.9943 0.9922 0.9891 1.0065 0.9785 0.9726 0.9616 0.9823 1.0823 1.0317 1.0437 1.0244 1.0087 1.0101 1.0155 0.9951 1.0035 1.0042 1.0065 0.9974 1.0011 1.0011 1.0018 1.0037 0.998 0.9966 0.9958 1.0092 0.9987 0.983 0.9777 0.9965 0.9171 0.9185 0.9327 0.8883 1.0136 1.0146 1.0234 0.9984 1.0061 1.0072 1.0114 0.9987 1.0033 1.0039 1.0062 1.005 1.0008 1.0003 1.0013 1.0114 0.9963 0.9911 0.9897 1.0072 0.9584 0.9741 0.9643 0.896 0.9285 1.0189 1.0308 1.0021 1.009 1.01 1.0166 0.9998 1.0056 1.0066 1.0106 1.006

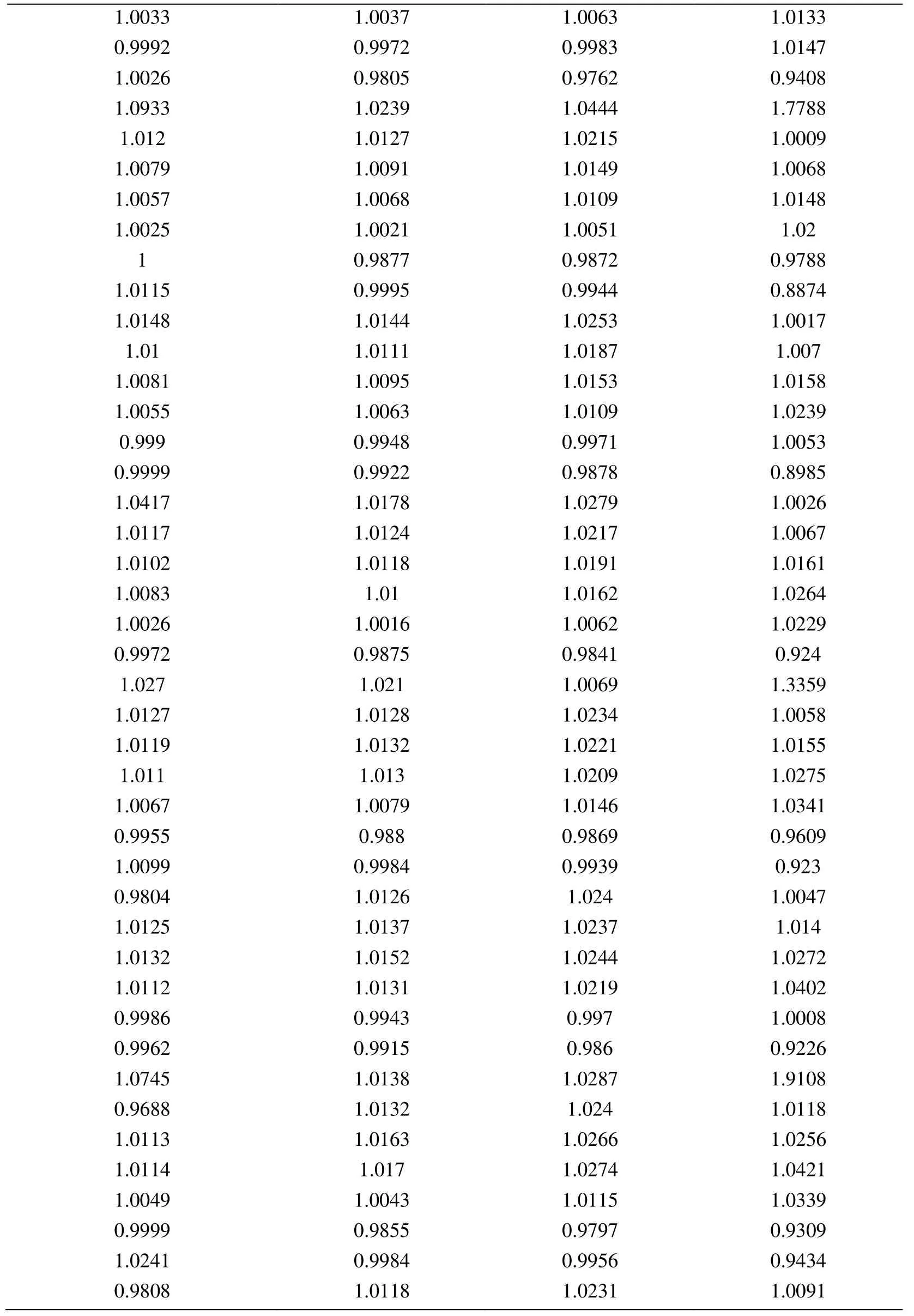
1.0033 1.0037 1.0063 1.0133 0.9992 0.9972 0.9983 1.0147 1.0026 0.9805 0.9762 0.9408 1.0933 1.0239 1.0444 1.7788 1.012 1.0127 1.0215 1.0009 1.0079 1.0091 1.0149 1.0068 1.0057 1.0068 1.0109 1.0148 1.0025 1.0021 1.0051 1.02 1 0.9877 0.9872 0.9788 1.0115 0.9995 0.9944 0.8874 1.0148 1.0144 1.0253 1.0017 1.01 1.0111 1.0187 1.007 1.0081 1.0095 1.0153 1.0158 1.0055 1.0063 1.0109 1.0239 0.999 0.9948 0.9971 1.0053 0.9999 0.9922 0.9878 0.8985 1.0417 1.0178 1.0279 1.0026 1.0117 1.0124 1.0217 1.0067 1.0102 1.0118 1.0191 1.0161 1.0083 1.01 1.0162 1.0264 1.0026 1.0016 1.0062 1.0229 0.9972 0.9875 0.9841 0.924 1.027 1.021 1.0069 1.3359 1.0127 1.0128 1.0234 1.0058 1.0119 1.0132 1.0221 1.0155 1.011 1.013 1.0209 1.0275 1.0067 1.0079 1.0146 1.0341 0.9955 0.988 0.9869 0.9609 1.0099 0.9984 0.9939 0.923 0.9804 1.0126 1.024 1.0047 1.0125 1.0137 1.0237 1.014 1.0132 1.0152 1.0244 1.0272 1.0112 1.0131 1.0219 1.0402 0.9986 0.9943 0.997 1.0008 0.9962 0.9915 0.986 0.9226 1.0745 1.0138 1.0287 1.9108 0.9688 1.0132 1.024 1.0118 1.0113 1.0163 1.0266 1.0256 1.0114 1.017 1.0274 1.0421 1.0049 1.0043 1.0115 1.0339 0.9999 0.9855 0.9797 0.9309 1.0241 0.9984 0.9956 0.9434 0.9808 1.0118 1.0231 1.0091

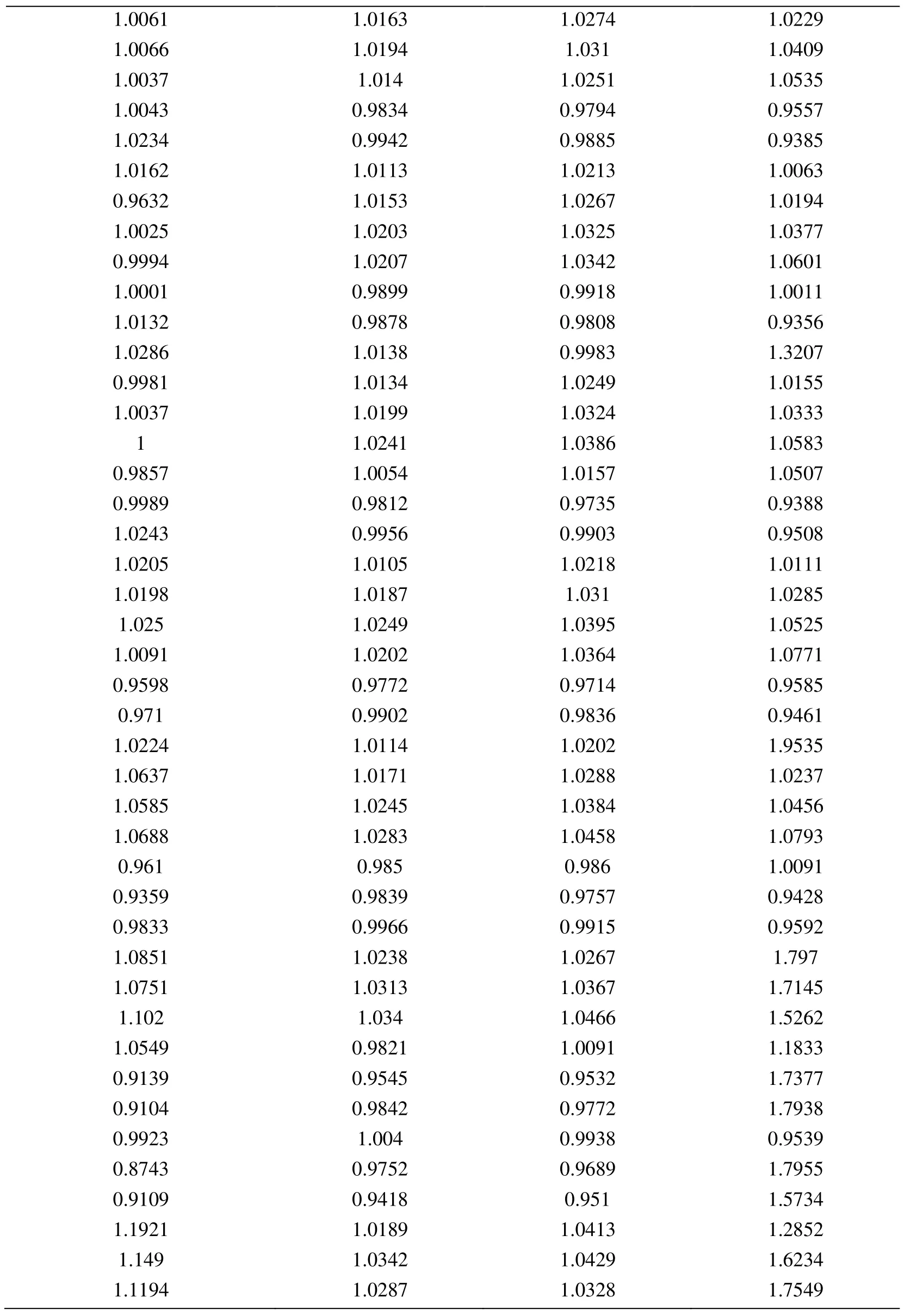
1.0061 1.0163 1.0274 1.0229 1.0066 1.0194 1.031 1.0409 1.0037 1.014 1.0251 1.0535 1.0043 0.9834 0.9794 0.9557 1.0234 0.9942 0.9885 0.9385 1.0162 1.0113 1.0213 1.0063 0.9632 1.0153 1.0267 1.0194 1.0025 1.0203 1.0325 1.0377 0.9994 1.0207 1.0342 1.0601 1.0001 0.9899 0.9918 1.0011 1.0132 0.9878 0.9808 0.9356 1.0286 1.0138 0.9983 1.3207 0.9981 1.0134 1.0249 1.0155 1.0037 1.0199 1.0324 1.0333 1 1.0241 1.0386 1.0583 0.9857 1.0054 1.0157 1.0507 0.9989 0.9812 0.9735 0.9388 1.0243 0.9956 0.9903 0.9508 1.0205 1.0105 1.0218 1.0111 1.0198 1.0187 1.031 1.0285 1.025 1.0249 1.0395 1.0525 1.0091 1.0202 1.0364 1.0771 0.9598 0.9772 0.9714 0.9585 0.971 0.9902 0.9836 0.9461 1.0224 1.0114 1.0202 1.9535 1.0637 1.0171 1.0288 1.0237 1.0585 1.0245 1.0384 1.0456 1.0688 1.0283 1.0458 1.0793 0.961 0.985 0.986 1.0091 0.9359 0.9839 0.9757 0.9428 0.9833 0.9966 0.9915 0.9592 1.0851 1.0238 1.0267 1.797 1.0751 1.0313 1.0367 1.7145 1.102 1.034 1.0466 1.5262 1.0549 0.9821 1.0091 1.1833 0.9139 0.9545 0.9532 1.7377 0.9104 0.9842 0.9772 1.7938 0.9923 1.004 0.9938 0.9539 0.8743 0.9752 0.9689 1.7955 0.9109 0.9418 0.951 1.5734 1.1921 1.0189 1.0413 1.2852 1.149 1.0342 1.0429 1.6234 1.1194 1.0287 1.0328 1.7549

1.0563 1.0223 1.0213 1.8139 0.9451 0.9924 0.9863 0.9525 0.8937 0.9774 0.9686 0.9447 1.0447 1.011 1.0243 1.0719 1.0973 1.0281 1.0442 1.0647 1.0763 1.0217 1.0345 1.0358 1.0524 1.0135 1.0246 1.0165 1.0413 0.9957 0.9922 0.9571 1.0083 0.984 0.9761 0.9402 0.9227 0.9894 0.9933 1.0173 0.7948 1.0259 1.0425 1.0715 0.8759 1.0226 1.0361 1.0416 0.9863 1.0157 1.0275 1.0212 1.0371 1.0085 1.0217 1.948 0.9827 0.9905 0.984 0.9428 1.232 0.98 0.9757 0.9641 1.1544 1.0197 1.0345 1.0698 1.0413 1.0229 1.0365 1.0473 1.0066 1.0175 1.0294 1.0256 1.0315 1.0105 1.0218 1.0096 1.015 0.9962 0.991 0.9474 0.9699 0.982 0.975 0.9383 1.0051 1.0079 1.0181 1.0499 1.0186 1.0218 1.0349 1.0515 1.017 1.0185 1.0303 1.0297 0.9916 1.0129 1.0242 1.0134 1.0306 1.0154 0.9999 1.3267 1.095 0.988 0.9814 0.9315 0.9951 0.9943 0.9978 1.0095 1.0152 1.0186 1.0305 1.0523 1.0164 1.0185 1.0298 1.0331 0.9811 1.0145 1.0256 1.0168 1.0115 1.0123 1.0223 1.0055 1.1451 0.9946 0.9892 0.9329 0.9912 0.9861 0.984 0.9643 1.0103 1.0129 1.0227 1.0471 1.0149 1.0173 1.0276 1.0354 1.014 1.0152 1.0256 1.0196 0.932 1.0121 1.0233 1.0075 1.0299 0.9992 0.9966 0.9375 1.0126 0.9861 0.9814 0.932 1.0045 1.0052 1.012 1.0329 1.0124 1.0148 1.0238 1.0358

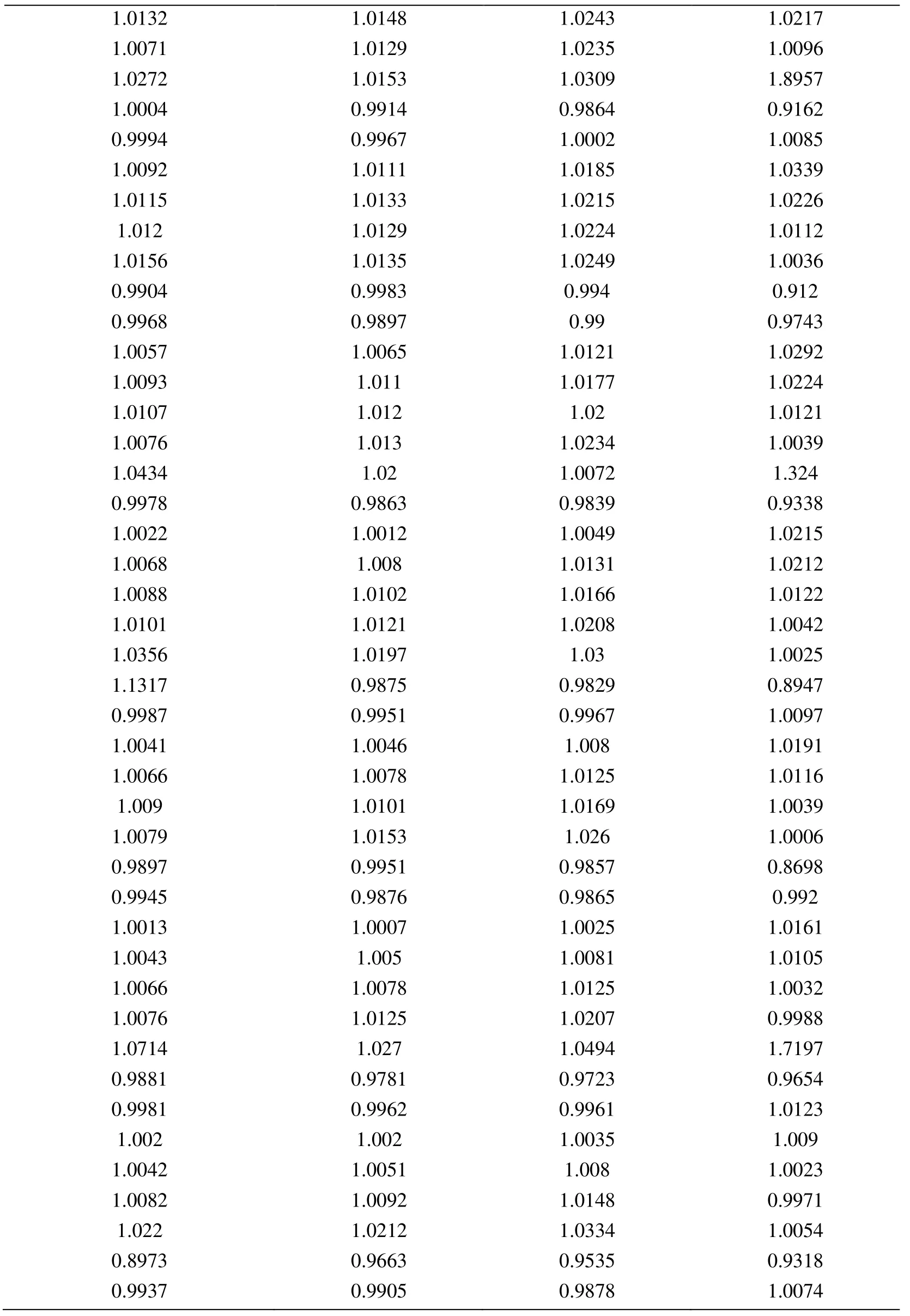
1.0132 1.0148 1.0243 1.0217 1.0071 1.0129 1.0235 1.0096 1.0272 1.0153 1.0309 1.8957 1.0004 0.9914 0.9864 0.9162 0.9994 0.9967 1.0002 1.0085 1.0092 1.0111 1.0185 1.0339 1.0115 1.0133 1.0215 1.0226 1.012 1.0129 1.0224 1.0112 1.0156 1.0135 1.0249 1.0036 0.9904 0.9983 0.994 0.912 0.9968 0.9897 0.99 0.9743 1.0057 1.0065 1.0121 1.0292 1.0093 1.011 1.0177 1.0224 1.0107 1.012 1.02 1.0121 1.0076 1.013 1.0234 1.0039 1.0434 1.02 1.0072 1.324 0.9978 0.9863 0.9839 0.9338 1.0022 1.0012 1.0049 1.0215 1.0068 1.008 1.0131 1.0212 1.0088 1.0102 1.0166 1.0122 1.0101 1.0121 1.0208 1.0042 1.0356 1.0197 1.03 1.0025 1.1317 0.9875 0.9829 0.8947 0.9987 0.9951 0.9967 1.0097 1.0041 1.0046 1.008 1.0191 1.0066 1.0078 1.0125 1.0116 1.009 1.0101 1.0169 1.0039 1.0079 1.0153 1.026 1.0006 0.9897 0.9951 0.9857 0.8698 0.9945 0.9876 0.9865 0.992 1.0013 1.0007 1.0025 1.0161 1.0043 1.005 1.0081 1.0105 1.0066 1.0078 1.0125 1.0032 1.0076 1.0125 1.0207 0.9988 1.0714 1.027 1.0494 1.7197 0.9881 0.9781 0.9723 0.9654 0.9981 0.9962 0.9961 1.0123 1.002 1.002 1.0035 1.009 1.0042 1.0051 1.008 1.0023 1.0082 1.0092 1.0148 0.9971 1.022 1.0212 1.0334 1.0054 0.8973 0.9663 0.9535 0.9318 0.9937 0.9905 0.9878 1.0074

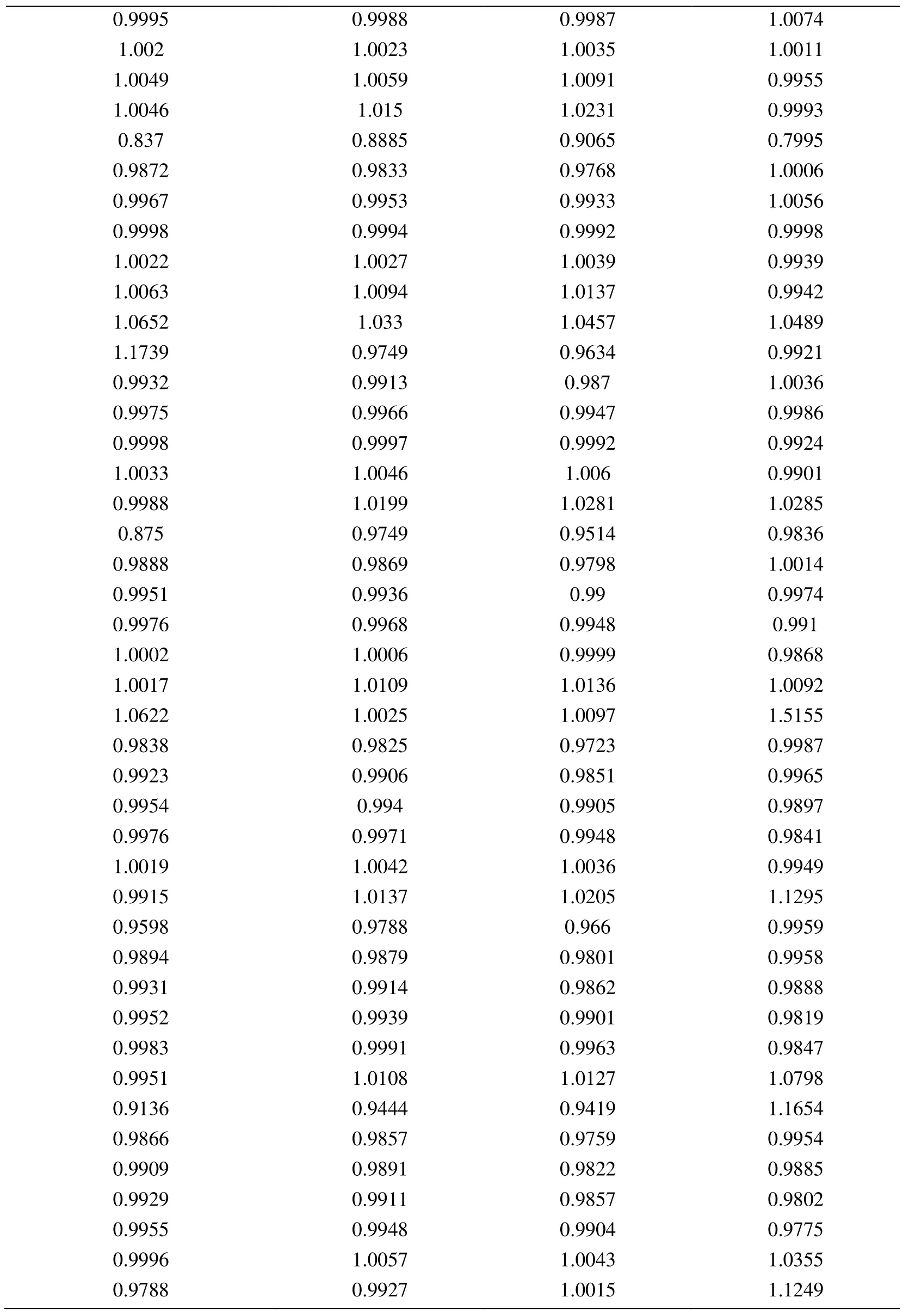
0.9995 0.9988 0.9987 1.0074 1.002 1.0023 1.0035 1.0011 1.0049 1.0059 1.0091 0.9955 1.0046 1.015 1.0231 0.9993 0.837 0.8885 0.9065 0.7995 0.9872 0.9833 0.9768 1.0006 0.9967 0.9953 0.9933 1.0056 0.9998 0.9994 0.9992 0.9998 1.0022 1.0027 1.0039 0.9939 1.0063 1.0094 1.0137 0.9942 1.0652 1.033 1.0457 1.0489 1.1739 0.9749 0.9634 0.9921 0.9932 0.9913 0.987 1.0036 0.9975 0.9966 0.9947 0.9986 0.9998 0.9997 0.9992 0.9924 1.0033 1.0046 1.006 0.9901 0.9988 1.0199 1.0281 1.0285 0.875 0.9749 0.9514 0.9836 0.9888 0.9869 0.9798 1.0014 0.9951 0.9936 0.99 0.9974 0.9976 0.9968 0.9948 0.991 1.0002 1.0006 0.9999 0.9868 1.0017 1.0109 1.0136 1.0092 1.0622 1.0025 1.0097 1.5155 0.9838 0.9825 0.9723 0.9987 0.9923 0.9906 0.9851 0.9965 0.9954 0.994 0.9905 0.9897 0.9976 0.9971 0.9948 0.9841 1.0019 1.0042 1.0036 0.9949 0.9915 1.0137 1.0205 1.1295 0.9598 0.9788 0.966 0.9959 0.9894 0.9879 0.9801 0.9958 0.9931 0.9914 0.9862 0.9888 0.9952 0.9939 0.9901 0.9819 0.9983 0.9991 0.9963 0.9847 0.9951 1.0108 1.0127 1.0798 0.9136 0.9444 0.9419 1.1654 0.9866 0.9857 0.9759 0.9954 0.9909 0.9891 0.9822 0.9885 0.9929 0.9911 0.9857 0.9802 0.9955 0.9948 0.9904 0.9775 0.9996 1.0057 1.0043 1.0355 0.9788 0.9927 1.0015 1.1249

1.0693 0.9842 0.9727 0.9951 0.9889 0.9874 0.9788 0.9888 0.9907 0.9886 0.9817 0.9794 0.9928 0.9909 0.985 0.9725 0.9977 1.0002 0.9964 1.0029 0.9929 1.0043 1.0084 1.1177 0.9434 0.9862 0.9708 0.9947 0.9874 0.9865 0.9764 0.9898 0.9887 0.9867 0.9783 0.9796 0.9901 0.9876 0.9802 0.9696 0.9946 0.9941 0.9881 0.98 1.003 1.0087 1.0115 1.0954 0.9749 0.9888 0.9821 2.0232 0.9866 0.9863 0.9753 0.9912 0.9873 0.9856 0.976 0.9808 0.9877 0.985 0.9762 0.9685 0.9908 0.9885 0.9804 0.9654 1.0022 1.0075 1.0077 1.0578 0.9895 1.0012 1.0061 1.0892 0.9509 0.9868 0.9751 0.9928 0.9898 0.9855 0.9749 0.983 0.9881 0.9834 0.9733 0.9694 0.99 0.9839 0.974 0.9577 1.0011 1.0004 0.9964 1.0121 1.0017 1.008 1.0139 1.0933 0.9331 0.9714 0.9637 1.2748 1.0398 0.9863 0.9751 0.9858 0.9925 0.9828 0.9719 0.9716 0.994 0.9808 0.9695 0.9555 1.0014 0.9903 0.9817 0.972 0.9997 1.0131 1.0191 1.0886 0.9755 0.9979 1.0052 1.0657 1.0254 0.9878 0.9764 0.9889 0.9971 0.9832 0.9718 0.9749 0.998 0.9792 0.9671 0.957 1.0035 0.9816 0.9694 0.9481 0.9994 1.0134 1.017 1.065 0.9784 1.0062 1.0124 1.0731 0.9745 0.9912 0.9783 0.9919 1.0292 0.9845 0.9729 0.9788 0.9981 0.979 0.9665 0.9608 1.0016 0.9764 0.9622 0.9401 1.0038 1.0037 1.0007 1.0141

0.9891 1.0125 1.0201 1.0796 0.9749 0.9972 0.9946 2.0152 0.9739 0.9865 0.9751 0.9831 0.9848 0.9798 0.9673 0.9655 0.9807 0.9745 0.9597 0.9419 0.9851 0.9871 0.9754 0.9565 1.0033 1.0186 1.0269 1.0807 0.9921 1.005 1.0108 1.0578 0.9576 0.9894 0.9782 0.9877 0.9746 0.9813 0.9691 0.9706 0.9485 0.9746 0.96 0.9478 0.9388 0.9748 0.9579 0.9268 1.0288 1.0204 1.0263 1.0629 1.0491 1.0105 1.0178 1.065 0.9664 0.9877 0.9752 1.3226 0.9264 0.9856 0.9715 0.9756 0.9285 0.9801 0.9619 0.9547 0.9053 0.9777 0.9522 0.9242 1.0144 1.0099 1.0049 1.0057 1.0767 1.0114 1.026 1.072 1.0294 1.0041 1.0095 1.0474 0.9192 0.9566 0.9439 1.0666 0.9236 0.9385 0.9313 0.9736 0.8955 0.9117 0.9167 0.8524 0.9378 0.9226 0.9438 0.8767 1.0996 1.0611 1.034 1.2069 1.1114 1.0381 1.0081 1.1036 1.1327 1.0309 1.0009 1.0681 1.159 1.054 1.0233 1.1683 1.1021 1.0057 1.0064 1.1029 0.8364 0.8994 0.9131 0.8029 0.871 0.9293 0.9258 0.9295 0.8816 0.9497 0.9388 1.0314 0.997 1.0077 0.9644 1.6694 1.0995 1.0058 1.0183 1.0615 1.1296 1.0191 1.0309 1.0667 0.8575 0.9826 0.9563 0.9214 0.8666 0.9784 0.9576 0.9435 0.8985 0.9832 0.9678 0.9681 0.9276 0.9903 0.9778 0.9861 1.0178 1.0056 1.0115 1.0545 0.9808 1.0197 1.0286 1.0784 0.8703 0.9899 0.9785 0.9592

0.9321 0.9725 0.9564 0.9361 0.9642 0.9786 0.9656 0.9625 0.9718 0.9859 0.9744 0.9812 0.9774 0.9984 0.9962 2.0099 1.0319 1.013 1.0209 1.0748 1.1903 1.0088 1.0078 1.0251 1.2893 0.9743 0.9586 0.9333 1.1885 0.9774 0.9642 0.9569 1.0523 0.9837 0.9719 0.9766 0.9751 0.9919 0.9793 0.9913 1.0098 1.0068 1.0132 1.0678 1.0129 1.0167 1.0222 1.0714 0.9852 0.9804 0.967 0.9433 0.9805 0.9773 0.964 0.9521 0.9835 0.9822 0.9703 0.9722 0.9683 0.988 0.9766 0.9876 0.9814 0.9991 1.0063 1.0605 0.9997 1.0143 1.0215 1.0865 0.9941 0.9914 0.9829 0.975 0.9823 0.9785 0.9659 0.9495 0.9834 0.9814 0.9698 0.9682 1.0201 0.9861 0.9747 0.9839 0.963 0.9745 0.9663 1.2868 0.8732 1.0084 1.0148 1.0859 1.0022 1.0036 1.0012 1.0243 0.9855 0.9817 0.9704 0.9518 0.9842 0.9816 0.9707 0.9651 0.992 0.9849 0.9739 0.9805 1.0233 0.9877 0.9762 0.9919 1.0187 1.002 1.0071 1.0799 1.0039 1.0103 1.0126 1.07 0.9898 0.987 0.9779 0.962 0.9859 0.983 0.973 0.9637 0.9862 0.9845 0.9743 0.9778 1.0368 0.9867 0.9755 0.9897 0.9702 0.9909 0.9853 2.0277 1.0007 1.0095 1.0139 1.0973 0.9946 0.9939 0.9874 0.9825 0.9883 0.9855 0.9768 0.9644 0.9873 0.9852 0.976 0.9759 0.9894 0.9863 0.9758 0.9876 0.9666 0.9874 0.9728 0.9943 1.0727 1.0041 1.0087 1.1074

0.9982 1.0011 0.9975 1.0142 0.9912 0.989 0.9819 0.968 0.9891 0.9868 0.9789 0.9753 0.9881 0.9866 0.9774 0.986 0.9864 0.9853 0.9738 0.9939 0.9707 0.9927 1.0009 1.1064 0.9991 1.0066 1.0059 1.0552 0.9943 0.9932 0.9877 0.9748 0.9913 0.9892 0.9828 0.9759 0.9897 0.9879 0.9801 0.9851 0.9919 0.986 0.9758 0.9934 0.9468 0.9524 0.9481 1.1983 0.9964 1.0086 1.0106 1.1004 0.9972 0.998 0.9942 0.9854 0.9937 0.9921 0.9872 0.9776 0.9917 0.9899 0.9837 0.9851 0.9898 0.9875 0.9791 0.9932 0.9679 0.981 0.9686 0.9959 0.9148 1.0061 1.0111 1.1396 1.0001 1.0034 1.0016 1.001 0.9962 0.9954 0.992 0.9804 0.994 0.9923 0.9878 0.9858 0.9913 0.9896 0.9831 0.9933 0.9924 0.9836 0.9731 0.9975 1.0578 0.9887 0.9851 1.7523 1.0037 1.01 1.0112 1.0239 0.9988 0.9991 0.9972 0.9841 0.9962 0.9951 0.9921 0.9871 0.9938 0.9922 0.9877 0.9939 0.9921 0.9868 0.9789 0.9991 0.9325 0.978 0.957 0.9907 1.109 1.0181 1.0247 1.0555 1.0019 1.0034 1.0035 0.9888 0.9984 0.998 0.9965 0.9886 0.9962 0.995 0.9922 0.9949 0.9922 0.9904 0.9851 1.0006 0.9806 0.9775 0.9659 0.9963 1.0869 1.0301 1.0435 1.0907 1.0063 1.0086 1.0116 0.9949 1.0008 1.0012 1.0013 0.9904 0.9985 0.9978 0.9966 0.996 0.9955 0.994 0.991 1.0021 0.9954 0.9839 0.9763 1.0015

0.8788 0.8887 0.9026 0.8685 1.0127 1.0153 1.0224 1.0028 1.0036 1.0046 1.0066 0.9924 1.0007 1.0007 1.0009 0.9973 0.9983 0.9973 0.9962 1.0036 0.9938 0.9899 0.986 1.006 0.9384 0.966 0.9519 0.964 0.8854 1.0229 1.0351 1.0119 1.0071 1.0084 1.0129 0.9947 1.0029 1.0035 1.0054 0.9986 1.0006 1.0004 1.0009 1.005 0.9969 0.995 0.9938 1.0095 0.9984 0.9776 0.9704 0.9837 1.1354 1.0302 1.055 1.6356 1.0113 1.0124 1.0199 0.9972 1.0054 1.0064 1.0101 0.9998 1.0029 1.0033 1.0053 1.0063 1.0001 0.9992 0.9999 1.0122 0.9981 0.9874 0.985 1 0.9567 0.9875 0.9703 0.8688 1.0245 1.0164 1.0269 1.0002 1.008 1.0091 1.015 1.0008 1.0051 1.0061 1.0097 1.0075 1.0028 1.0029 1.0052 1.0145 0.9978 0.9947 0.9953 1.0113 0.9915 0.9807 0.9748 0.9058 1.0534 1.022 1.0325 1.0031 1.0107 1.0116 1.0196 1.0016 1.0074 1.0087 1.014 1.0083 1.0053 1.0062 1.0101 1.0164 1.0014 1.0003 1.003 1.019 1.0018 0.9848 0.9828 0.9512 1.0216 1.0147 1.0046 1.2925 1.0131 1.0134 1.0234 1.0021 1.0095 1.0108 1.0179 1.0087 1.0077 1.0091 1.0146 1.0177 1.0046 1.005 1.0094 1.0244 0.9986 0.991 0.992 0.9877 1.007 0.9969 0.9926 0.8984 0.9601 1.0145 1.0261 1.0026 1.0113 1.0122 1.0211 1.0084 1.0099 1.0116 1.0187 1.0182 1.0077 1.0092 1.0152 1.028

1.0005 0.998 1.0016 1.0135 0.9978 0.9902 0.9859 0.9107 1.0597 1.017 1.0335 1.8769 1.0124 1.0127 1.0229 1.0074 1.0118 1.0133 1.0219 1.0178 1.0106 1.0126 1.0203 1.0299 1.0047 1.0051 1.0112 1.0307 0.9948 0.9867 0.9835 0.937 1.0201 1 0.9975 0.9297 1.005 1.0125 1.0236 1.006 1.0128 1.0141 1.0239 1.0165 1.0131 1.0152 1.0244 1.0301 1.0099 1.0115 1.0199 1.0408 0.9957 0.9891 0.9889 0.9752 1.0013 0.9949 0.9897 0.9261 1.0463 1.0134 1.0234 1.0047 0.9912 1.0139 1.0245 1.0143 1.0116 1.0167 1.027 1.0287 1.0109 1.0164 1.0267 1.0451 1.0021 0.9976 1.0023 1.0161 1.0026 0.9882 0.9821 0.9273 1.0182 1.0171 1.0017 1.3321 0.9586 1.0127 1.0238 1.0115 1.0064 1.0171 1.0282 1.0261 1.0064 1.0195 1.0313 1.045 1.0026 1.0092 1.0188 1.0473 1.0057 0.983 0.9771 0.9393 1.0312 0.9968 0.9918 0.9433 0.993 1.0107 1.022 1.0083 0.9983 1.0164 1.0279 1.0227 1.0022 1.021 1.0335 1.0421 0.9984 1.0186 1.0318 1.062 1.0036 0.9834 0.9809 0.9717 1.0173 0.9909 0.9845 0.9389 1.0299 1.0098 1.0232 1.9413 0.9846 1.0148 1.0264 1.0187 1.0035 1.021 1.0338 1.0376 0.998 1.0239 1.0388 1.0638 0.9848 0.9947 1.0001 1.0244 0.9994 0.9843 0.9766 0.9374 1.0319 0.9963 0.9929 0.9546 1.0365 1.0124 1.0238 1.0144 1.0229 1.0201 1.0327 1.0326

1.0247 1.0257 1.041 1.0587 0.9972 1.0126 1.0268 1.0695 0.9641 0.9779 0.9702 0.945 0.9788 0.9928 0.9868 0.9499 1.0461 1.0101 1.0198 1.0094 1.0476 1.0187 1.0307 1.0275 1.0615 1.0259 1.0404 1.0513 1.0644 1.0261 1.0437 1.0843 0.938 0.9776 0.973 0.9761 0.9327 0.9871 0.9796 0.9455 1.0196 1.0107 0.9943 1.3017 1.0869 1.0257 1.0289 1.7852 1.0798 1.0325 1.0387 1.6891 1.107 1.0321 1.0474 1.4595 1.0049 0.9594 0.9834 1.2704 0.9209 0.9623 0.9585 1.7716 0.924 0.9876 0.9805 1.7891 0.9301 0.9861 0.9833 1.783 0.8791 0.9693 0.9639 1.7886 0.9718 0.9447 0.9618 1.4265 1.1915 1.0277 1.0463 1.3778 1.1389 1.0334 1.0408 1.6592 1.1217 1.0273 1.0309 1.7712 1.0043 1 1.0188 2.6762 0.9291 0.9899 0.9832 0.9489 0.8923 0.9757 0.968 0.9548 1.0779 1.0207 1.0372 1.0837 1.0933 1.0271 1.0423 1.0577 1.0696 1.0202 1.0326 1.0315 1.0434 1.0113 1.0223 1.0129 1.0013 0.995 0.9897 0.9536 1.0889 0.9806 0.9725 0.9401 0.8426 1.0015 1.0114 1.0492 0.8142 1.0262 1.0422 1.0652 0.8864 1.0214 1.0344 1.0369 0.9964 1.0141 1.0257 1.0177 1.0204 1.0122 0.9968 1.3144 0.9876 0.9875 0.9803 0.9393 1.2572 0.9852 0.9852 0.9921 1.1195 1.0227 1.0378 1.0682 1.0313 1.022 1.0352 1.0422 0.9987 1.0162 1.0279 1.0221 1.0373 1.0105 1.0205 1.0072

1.0134 0.9937 0.9879 0.943 0.9855 0.9811 0.9755 0.9499 1.0108 1.0145 1.0268 1.0597 1.0187 1.0215 1.0343 1.0467 1.0163 1.0175 1.0291 1.0261 1.0024 1.0118 1.0231 1.0107 1.0277 0.9977 0.9947 0.948 1.0308 0.985 0.9784 0.9322 1.0012 1.0023 1.0095 1.0329 1.0162 1.0193 1.0312 1.0489 1.0161 1.0178 1.029 1.0295 0.9569 1.0136 1.0247 1.0141 1.03 1.0124 1.0267 1.923 1.1806 0.9914 0.9856 0.9288 0.994 0.991 0.9923 0.9912 1.0122 1.0151 1.0253 1.047 1.0149 1.0171 1.0274 1.032 1.0115 1.0145 1.0251 1.0169 0.9505 1.0118 1.0232 1.0059 0.9931 0.998 0.9934 0.9315 0.9955 0.9861 0.9832 0.95 1.0073 1.0089 1.0167 1.0389 1.0128 1.0151 1.0242 1.033 1.0131 1.0145 1.0241 1.019 1.0031 1.0126 1.0234 1.0077 1.0409 1.0203 1.0054 1.3384 0.9974 0.9881 0.9836 0.9216 1.0023 1.0014 1.0064 1.0228 1.01 1.0121 1.0196 1.0321 1.0117 1.0134 1.0217 1.0202 1.011 1.0128 1.0226 1.0092 1.0285 1.0161 1.0262 1.0032 1.0211 0.9942 0.9896 0.9079 0.9982 0.9936 0.9957 0.9973 1.0068 1.0081 1.0139 1.0291 1.0096 1.0114 1.0182 1.0203 1.011 1.0121 1.0205 1.0102 1.0082 1.0136 1.0246 1.003 1.0326 1.0008 0.9975 0.9053 0.9968 0.9876 0.9869 0.9625 1.0036 1.0034 1.0075 1.0239 1.0073 1.0086 1.0139 1.0195 1.0091 1.0105 1.0172 1.0104

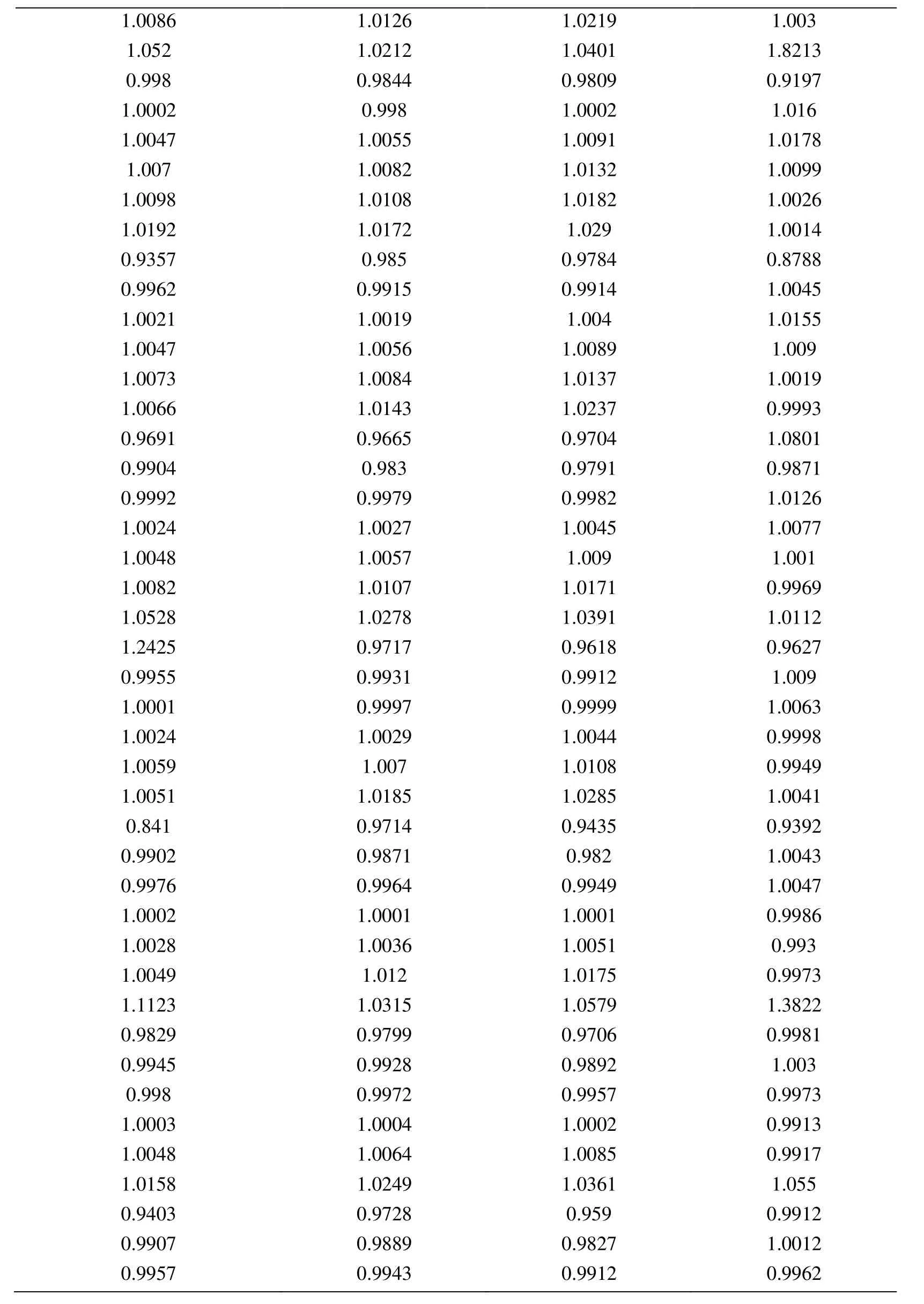
1.0086 1.0126 1.0219 1.003 1.052 1.0212 1.0401 1.8213 0.998 0.9844 0.9809 0.9197 1.0002 0.998 1.0002 1.016 1.0047 1.0055 1.0091 1.0178 1.007 1.0082 1.0132 1.0099 1.0098 1.0108 1.0182 1.0026 1.0192 1.0172 1.029 1.0014 0.9357 0.985 0.9784 0.8788 0.9962 0.9915 0.9914 1.0045 1.0021 1.0019 1.004 1.0155 1.0047 1.0056 1.0089 1.009 1.0073 1.0084 1.0137 1.0019 1.0066 1.0143 1.0237 0.9993 0.9691 0.9665 0.9704 1.0801 0.9904 0.983 0.9791 0.9871 0.9992 0.9979 0.9982 1.0126 1.0024 1.0027 1.0045 1.0077 1.0048 1.0057 1.009 1.001 1.0082 1.0107 1.0171 0.9969 1.0528 1.0278 1.0391 1.0112 1.2425 0.9717 0.9618 0.9627 0.9955 0.9931 0.9912 1.009 1.0001 0.9997 0.9999 1.0063 1.0024 1.0029 1.0044 0.9998 1.0059 1.007 1.0108 0.9949 1.0051 1.0185 1.0285 1.0041 0.841 0.9714 0.9435 0.9392 0.9902 0.9871 0.982 1.0043 0.9976 0.9964 0.9949 1.0047 1.0002 1.0001 1.0001 0.9986 1.0028 1.0036 1.0051 0.993 1.0049 1.012 1.0175 0.9973 1.1123 1.0315 1.0579 1.3822 0.9829 0.9799 0.9706 0.9981 0.9945 0.9928 0.9892 1.003 0.998 0.9972 0.9957 0.9973 1.0003 1.0004 1.0002 0.9913 1.0048 1.0064 1.0085 0.9917 1.0158 1.0249 1.0361 1.055 0.9403 0.9728 0.959 0.9912 0.9907 0.9889 0.9827 1.0012 0.9957 0.9943 0.9912 0.9962

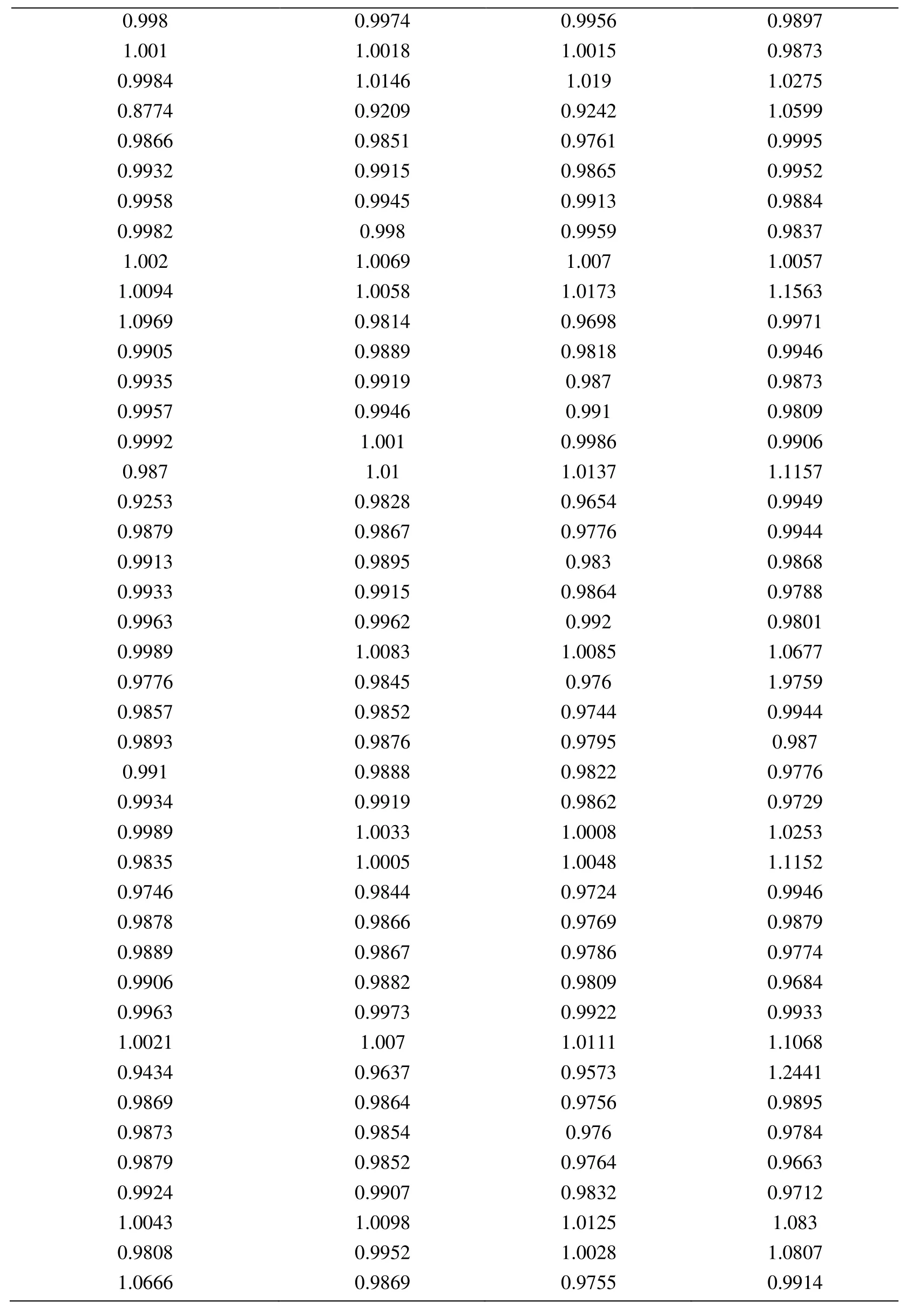
0.998 0.9974 0.9956 0.9897 1.001 1.0018 1.0015 0.9873 0.9984 1.0146 1.019 1.0275 0.8774 0.9209 0.9242 1.0599 0.9866 0.9851 0.9761 0.9995 0.9932 0.9915 0.9865 0.9952 0.9958 0.9945 0.9913 0.9884 0.9982 0.998 0.9959 0.9837 1.002 1.0069 1.007 1.0057 1.0094 1.0058 1.0173 1.1563 1.0969 0.9814 0.9698 0.9971 0.9905 0.9889 0.9818 0.9946 0.9935 0.9919 0.987 0.9873 0.9957 0.9946 0.991 0.9809 0.9992 1.001 0.9986 0.9906 0.987 1.01 1.0137 1.1157 0.9253 0.9828 0.9654 0.9949 0.9879 0.9867 0.9776 0.9944 0.9913 0.9895 0.983 0.9868 0.9933 0.9915 0.9864 0.9788 0.9963 0.9962 0.992 0.9801 0.9989 1.0083 1.0085 1.0677 0.9776 0.9845 0.976 1.9759 0.9857 0.9852 0.9744 0.9944 0.9893 0.9876 0.9795 0.987 0.991 0.9888 0.9822 0.9776 0.9934 0.9919 0.9862 0.9729 0.9989 1.0033 1.0008 1.0253 0.9835 1.0005 1.0048 1.1152 0.9746 0.9844 0.9724 0.9946 0.9878 0.9866 0.9769 0.9879 0.9889 0.9867 0.9786 0.9774 0.9906 0.9882 0.9809 0.9684 0.9963 0.9973 0.9922 0.9933 1.0021 1.007 1.0111 1.1068 0.9434 0.9637 0.9573 1.2441 0.9869 0.9864 0.9756 0.9895 0.9873 0.9854 0.976 0.9784 0.9879 0.9852 0.9764 0.9663 0.9924 0.9907 0.9832 0.9712 1.0043 1.0098 1.0125 1.083 0.9808 0.9952 1.0028 1.0807 1.0666 0.9869 0.9755 0.9914

0.9884 0.985 0.9746 0.9804 0.9882 0.9831 0.9731 0.9665 0.9912 0.985 0.9754 0.9583 1.0035 1.0062 1.0053 1.0423 0.9952 1.0048 1.0105 1.0873 0.9506 0.9896 0.976 0.9931 1.0195 0.9856 0.9745 0.9832 0.9926 0.9822 0.9712 0.9684 0.9948 0.981 0.9697 0.953 1.0034 0.9964 0.9904 0.9942 0.9959 1.0112 1.0178 1.09 0.9855 0.9945 0.9906 2.0244 1.03 0.987 0.9756 0.9865 0.997 0.9823 0.9708 0.9717 0.9987 0.9787 0.9664 0.9531 1.005 0.9854 0.9744 0.9568 0.9956 1.0153 1.0214 1.0813 0.9712 1.0036 1.0092 1.0666 0.9936 0.989 0.9777 0.99 1.0117 0.9833 0.9716 0.9756 0.9984 0.9781 0.9652 0.9565 1.0029 0.9776 0.9635 0.9393 1.0001 1.0122 1.0141 1.048 0.986 1.0096 1.0166 1.0739 0.9697 0.9797 0.9708 1.3067 0.9838 0.9851 0.9735 0.9799 0.9839 0.9786 0.9657 0.9614 0.9801 0.974 0.9587 0.937 0.9902 0.9976 0.9907 0.9873 1.0063 1.0161 1.0244 1.0794 0.9801 1.001 1.0081 1.0528 0.952 0.9876 0.9763 0.9845 0.9598 0.9799 0.9674 0.9667 0.9452 0.9735 0.9581 0.9421 0.9459 0.9803 0.965 0.936 1.0363 1.0215 1.0298 1.0759 1.0453 1.0079 1.0144 1.0596 0.9306 0.9873 0.9803 0.9896 0.9398 0.9843 0.9696 0.9719 0.9239 0.9792 0.9598 0.9494 0.905 0.9791 0.9525 0.92 1.0521 1.0171 1.0223 1.0438 1.0839 1.0084 1.022 1.0668

0.9806 0.991 0.9989 1.9987 0.9157 0.9531 0.9412 1.0493 0.9188 0.9341 0.9287 0.9522 0.89 0.9051 0.9142 0.8257 0.9915 0.9606 0.9744 0.9872 1.0928 1.0589 1.0292 1.1902 1.0937 1.0336 1.0042 1.085 1.1638 1.0336 1.0042 1.085 1.1553 1.0589 1.0292 1.1902 1.0181 0.9606 0.9744 0.9872 0.8387 0.9051 0.9142 0.8257 0.8787 0.9341 0.9287 0.9522 0.8805 0.9531 0.9412 1.0493 0.9847 0.991 0.9989 1.9987 1.1155 1.0084 1.022 1.0668 1.0984 1.0171 1.0223 1.0438 0.8439 0.9791 0.9525 0.92 0.8751 0.9792 0.9598 0.9494 0.9055 0.9843 0.9696 0.9719 0.9437 0.9873 0.9803 0.9896 1.037 1.0079 1.0144 1.0596 0.9581 1.0215 1.0298 1.0759 0.8779 0.9803 0.965 0.936 0.9411 0.9735 0.9581 0.9421 0.9681 0.9799 0.9674 0.9667 0.9715 0.9876 0.9763 0.9845 0.9788 1.001 1.0081 1.0528 1.0154 1.0161 1.0244 1.0794 1.2773 0.9976 0.9907 0.9873 1.2649 0.974 0.9587 0.937 1.1751 0.9786 0.9657 0.9614 1.0176 0.9851 0.9735 0.9799 0.9613 0.9797 0.9708 1.3067 1.0108 1.0096 1.0166 1.0739 1.0104 1.0122 1.0141 1.048 0.9824 0.9776 0.9635 0.9393 0.9809 0.9781 0.9652 0.9565 0.9971 0.9833 0.9716 0.9756 0.9628 0.989 0.9777 0.99 0.9865 1.0036 1.0092 1.0666 1.0165 1.0153 1.0214 1.0813 0.9892 0.9854 0.9744 0.9568 0.9822 0.9787 0.9664 0.9531

0.984 0.9823 0.9708 0.9717 1.0133 0.987 0.9756 0.9865 0.9736 0.9945 0.9906 2.0244 0.9089 1.0112 1.0178 1.09 0.9972 0.9964 0.9904 0.9942 0.9846 0.981 0.9697 0.953 0.9845 0.9822 0.9712 0.9684 1.0145 0.9856 0.9745 0.9832 0.9994 0.9896 0.976 0.9931 0.9579 1.0048 1.0105 1.0873 1.0025 1.0062 1.0053 1.0423 0.9882 0.985 0.9754 0.9583 0.9858 0.9831 0.9731 0.9665 0.9864 0.985 0.9746 0.9804 1.0444 0.9869 0.9755 0.9914 0.9753 0.9952 1.0028 1.0807 1.002 1.0098 1.0125 1.083 0.9924 0.9907 0.9832 0.9712 0.9879 0.9852 0.9764 0.9663 0.9873 0.9854 0.976 0.9784 0.9911 0.9864 0.9756 0.9895 0.9594 0.9637 0.9573 1.2441 0.9967 1.007 1.0111 1.1068 0.9963 0.9973 0.9922 0.9933 0.9906 0.9882 0.9809 0.9684 0.9889 0.9867 0.9786 0.9774 0.9885 0.9866 0.9769 0.9879 0.9744 0.9844 0.9724 0.9946 0.9967 1.0005 1.0048 1.1152 0.9985 1.0033 1.0008 1.0253 0.9934 0.9919 0.9862 0.9729 0.991 0.9888 0.9822 0.9776 0.9893 0.9876 0.9795 0.987 0.9919 0.9852 0.9744 0.9944 0.9828 0.9845 0.976 1.9759 0.9987 1.0083 1.0085 1.0677 0.9963 0.9962 0.992 0.9801 0.9933 0.9915 0.9864 0.9788 0.9913 0.9895 0.983 0.9868 0.9909 0.9867 0.9776 0.9944 0.9509 0.9828 0.9654 0.9949 1.1298 1.01 1.0137 1.1157 0.9992 1.001 0.9986 0.9906

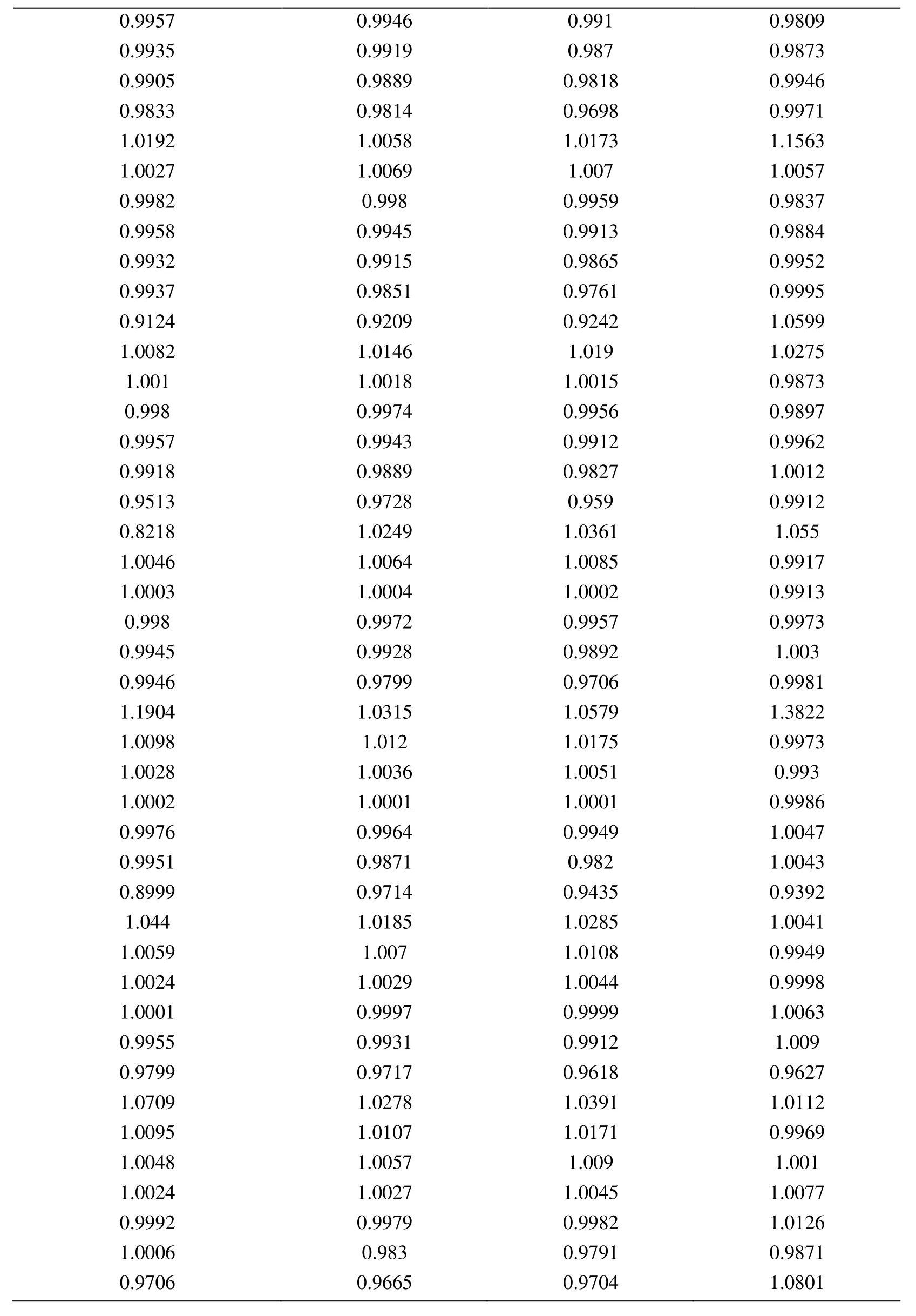
0.9957 0.9946 0.991 0.9809 0.9935 0.9919 0.987 0.9873 0.9905 0.9889 0.9818 0.9946 0.9833 0.9814 0.9698 0.9971 1.0192 1.0058 1.0173 1.1563 1.0027 1.0069 1.007 1.0057 0.9982 0.998 0.9959 0.9837 0.9958 0.9945 0.9913 0.9884 0.9932 0.9915 0.9865 0.9952 0.9937 0.9851 0.9761 0.9995 0.9124 0.9209 0.9242 1.0599 1.0082 1.0146 1.019 1.0275 1.001 1.0018 1.0015 0.9873 0.998 0.9974 0.9956 0.9897 0.9957 0.9943 0.9912 0.9962 0.9918 0.9889 0.9827 1.0012 0.9513 0.9728 0.959 0.9912 0.8218 1.0249 1.0361 1.055 1.0046 1.0064 1.0085 0.9917 1.0003 1.0004 1.0002 0.9913 0.998 0.9972 0.9957 0.9973 0.9945 0.9928 0.9892 1.003 0.9946 0.9799 0.9706 0.9981 1.1904 1.0315 1.0579 1.3822 1.0098 1.012 1.0175 0.9973 1.0028 1.0036 1.0051 0.993 1.0002 1.0001 1.0001 0.9986 0.9976 0.9964 0.9949 1.0047 0.9951 0.9871 0.982 1.0043 0.8999 0.9714 0.9435 0.9392 1.044 1.0185 1.0285 1.0041 1.0059 1.007 1.0108 0.9949 1.0024 1.0029 1.0044 0.9998 1.0001 0.9997 0.9999 1.0063 0.9955 0.9931 0.9912 1.009 0.9799 0.9717 0.9618 0.9627 1.0709 1.0278 1.0391 1.0112 1.0095 1.0107 1.0171 0.9969 1.0048 1.0057 1.009 1.001 1.0024 1.0027 1.0045 1.0077 0.9992 0.9979 0.9982 1.0126 1.0006 0.983 0.9791 0.9871 0.9706 0.9665 0.9704 1.0801

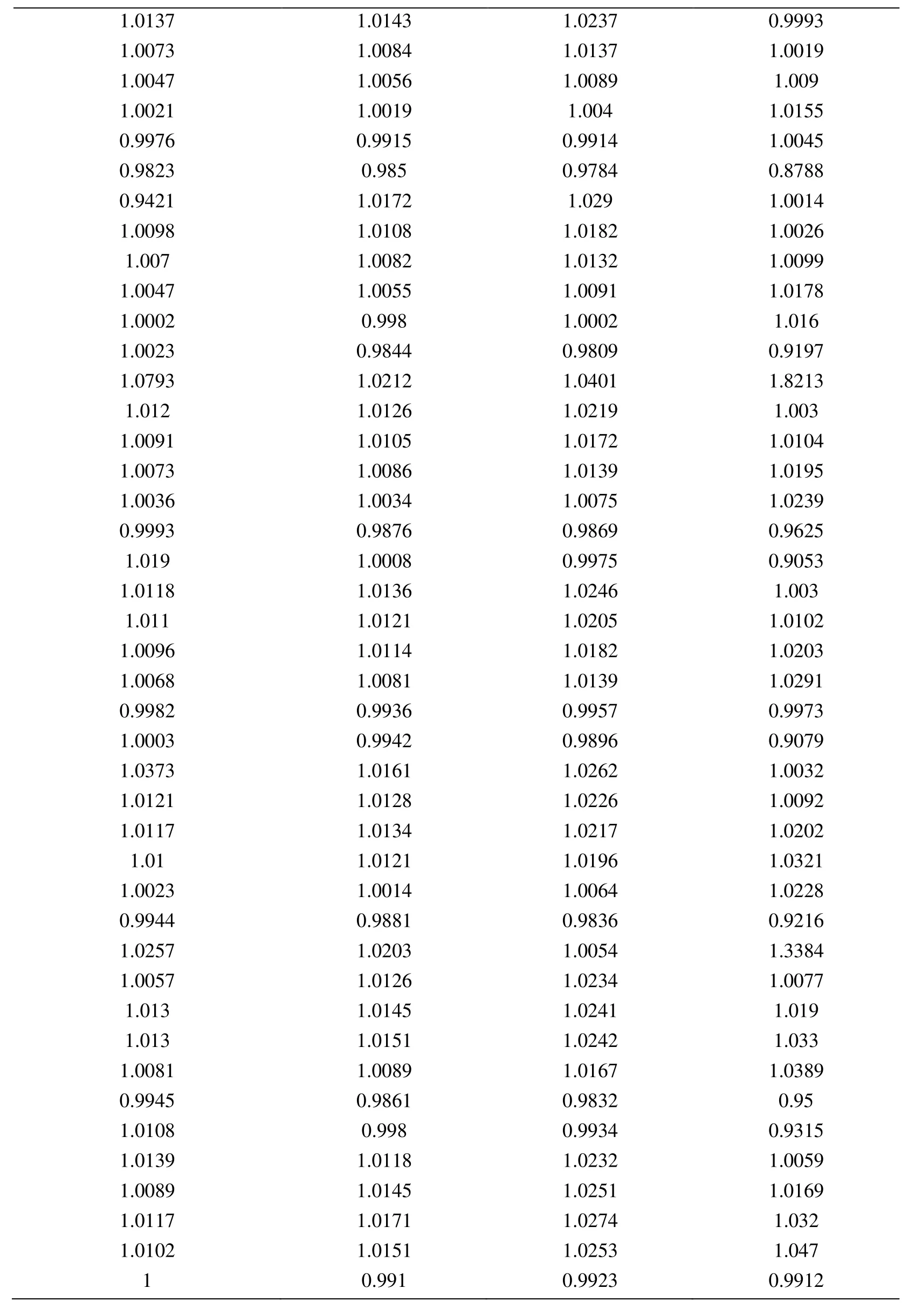
1.0137 1.0143 1.0237 0.9993 1.0073 1.0084 1.0137 1.0019 1.0047 1.0056 1.0089 1.009 1.0021 1.0019 1.004 1.0155 0.9976 0.9915 0.9914 1.0045 0.9823 0.985 0.9784 0.8788 0.9421 1.0172 1.029 1.0014 1.0098 1.0108 1.0182 1.0026 1.007 1.0082 1.0132 1.0099 1.0047 1.0055 1.0091 1.0178 1.0002 0.998 1.0002 1.016 1.0023 0.9844 0.9809 0.9197 1.0793 1.0212 1.0401 1.8213 1.012 1.0126 1.0219 1.003 1.0091 1.0105 1.0172 1.0104 1.0073 1.0086 1.0139 1.0195 1.0036 1.0034 1.0075 1.0239 0.9993 0.9876 0.9869 0.9625 1.019 1.0008 0.9975 0.9053 1.0118 1.0136 1.0246 1.003 1.011 1.0121 1.0205 1.0102 1.0096 1.0114 1.0182 1.0203 1.0068 1.0081 1.0139 1.0291 0.9982 0.9936 0.9957 0.9973 1.0003 0.9942 0.9896 0.9079 1.0373 1.0161 1.0262 1.0032 1.0121 1.0128 1.0226 1.0092 1.0117 1.0134 1.0217 1.0202 1.01 1.0121 1.0196 1.0321 1.0023 1.0014 1.0064 1.0228 0.9944 0.9881 0.9836 0.9216 1.0257 1.0203 1.0054 1.3384 1.0057 1.0126 1.0234 1.0077 1.013 1.0145 1.0241 1.019 1.013 1.0151 1.0242 1.033 1.0081 1.0089 1.0167 1.0389 0.9945 0.9861 0.9832 0.95 1.0108 0.998 0.9934 0.9315 1.0139 1.0118 1.0232 1.0059 1.0089 1.0145 1.0251 1.0169 1.0117 1.0171 1.0274 1.032 1.0102 1.0151 1.0253 1.047 1 0.991 0.9923 0.9912

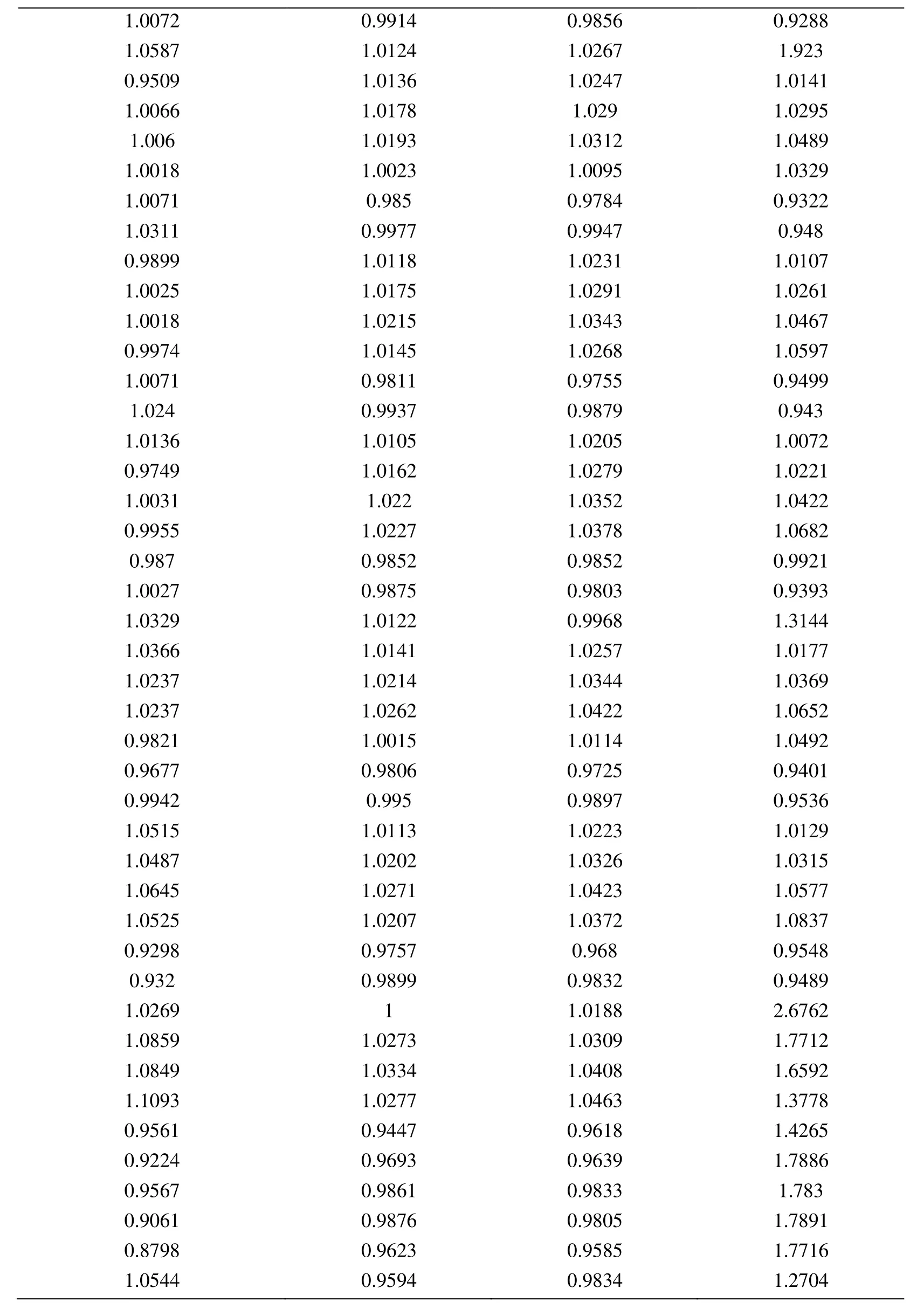
1.0072 0.9914 0.9856 0.9288 1.0587 1.0124 1.0267 1.923 0.9509 1.0136 1.0247 1.0141 1.0066 1.0178 1.029 1.0295 1.006 1.0193 1.0312 1.0489 1.0018 1.0023 1.0095 1.0329 1.0071 0.985 0.9784 0.9322 1.0311 0.9977 0.9947 0.948 0.9899 1.0118 1.0231 1.0107 1.0025 1.0175 1.0291 1.0261 1.0018 1.0215 1.0343 1.0467 0.9974 1.0145 1.0268 1.0597 1.0071 0.9811 0.9755 0.9499 1.024 0.9937 0.9879 0.943 1.0136 1.0105 1.0205 1.0072 0.9749 1.0162 1.0279 1.0221 1.0031 1.022 1.0352 1.0422 0.9955 1.0227 1.0378 1.0682 0.987 0.9852 0.9852 0.9921 1.0027 0.9875 0.9803 0.9393 1.0329 1.0122 0.9968 1.3144 1.0366 1.0141 1.0257 1.0177 1.0237 1.0214 1.0344 1.0369 1.0237 1.0262 1.0422 1.0652 0.9821 1.0015 1.0114 1.0492 0.9677 0.9806 0.9725 0.9401 0.9942 0.995 0.9897 0.9536 1.0515 1.0113 1.0223 1.0129 1.0487 1.0202 1.0326 1.0315 1.0645 1.0271 1.0423 1.0577 1.0525 1.0207 1.0372 1.0837 0.9298 0.9757 0.968 0.9548 0.932 0.9899 0.9832 0.9489 1.0269 1 1.0188 2.6762 1.0859 1.0273 1.0309 1.7712 1.0849 1.0334 1.0408 1.6592 1.1093 1.0277 1.0463 1.3778 0.9561 0.9447 0.9618 1.4265 0.9224 0.9693 0.9639 1.7886 0.9567 0.9861 0.9833 1.783 0.9061 0.9876 0.9805 1.7891 0.8798 0.9623 0.9585 1.7716 1.0544 0.9594 0.9834 1.2704

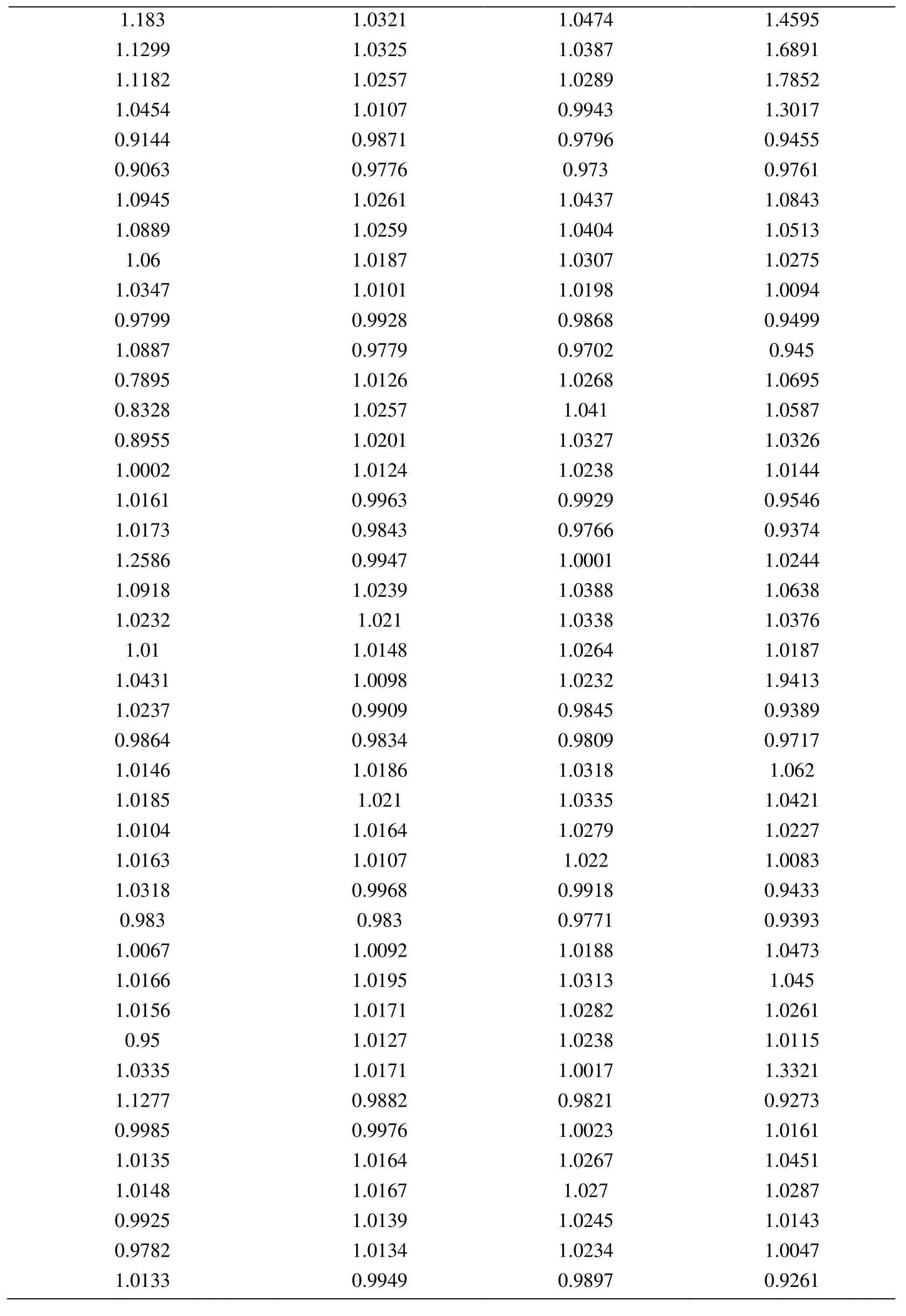
1.183 1.0321 1.0474 1.4595 1.1299 1.0325 1.0387 1.6891 1.1182 1.0257 1.0289 1.7852 1.0454 1.0107 0.9943 1.3017 0.9144 0.9871 0.9796 0.9455 0.9063 0.9776 0.973 0.9761 1.0945 1.0261 1.0437 1.0843 1.0889 1.0259 1.0404 1.0513 1.06 1.0187 1.0307 1.0275 1.0347 1.0101 1.0198 1.0094 0.9799 0.9928 0.9868 0.9499 1.0887 0.9779 0.9702 0.945 0.7895 1.0126 1.0268 1.0695 0.8328 1.0257 1.041 1.0587 0.8955 1.0201 1.0327 1.0326 1.0002 1.0124 1.0238 1.0144 1.0161 0.9963 0.9929 0.9546 1.0173 0.9843 0.9766 0.9374 1.2586 0.9947 1.0001 1.0244 1.0918 1.0239 1.0388 1.0638 1.0232 1.021 1.0338 1.0376 1.01 1.0148 1.0264 1.0187 1.0431 1.0098 1.0232 1.9413 1.0237 0.9909 0.9845 0.9389 0.9864 0.9834 0.9809 0.9717 1.0146 1.0186 1.0318 1.062 1.0185 1.021 1.0335 1.0421 1.0104 1.0164 1.0279 1.0227 1.0163 1.0107 1.022 1.0083 1.0318 0.9968 0.9918 0.9433 0.983 0.983 0.9771 0.9393 1.0067 1.0092 1.0188 1.0473 1.0166 1.0195 1.0313 1.045 1.0156 1.0171 1.0282 1.0261 0.95 1.0127 1.0238 1.0115 1.0335 1.0171 1.0017 1.3321 1.1277 0.9882 0.9821 0.9273 0.9985 0.9976 1.0023 1.0161 1.0135 1.0164 1.0267 1.0451 1.0148 1.0167 1.027 1.0287 0.9925 1.0139 1.0245 1.0143 0.9782 1.0134 1.0234 1.0047 1.0133 0.9949 0.9897 0.9261

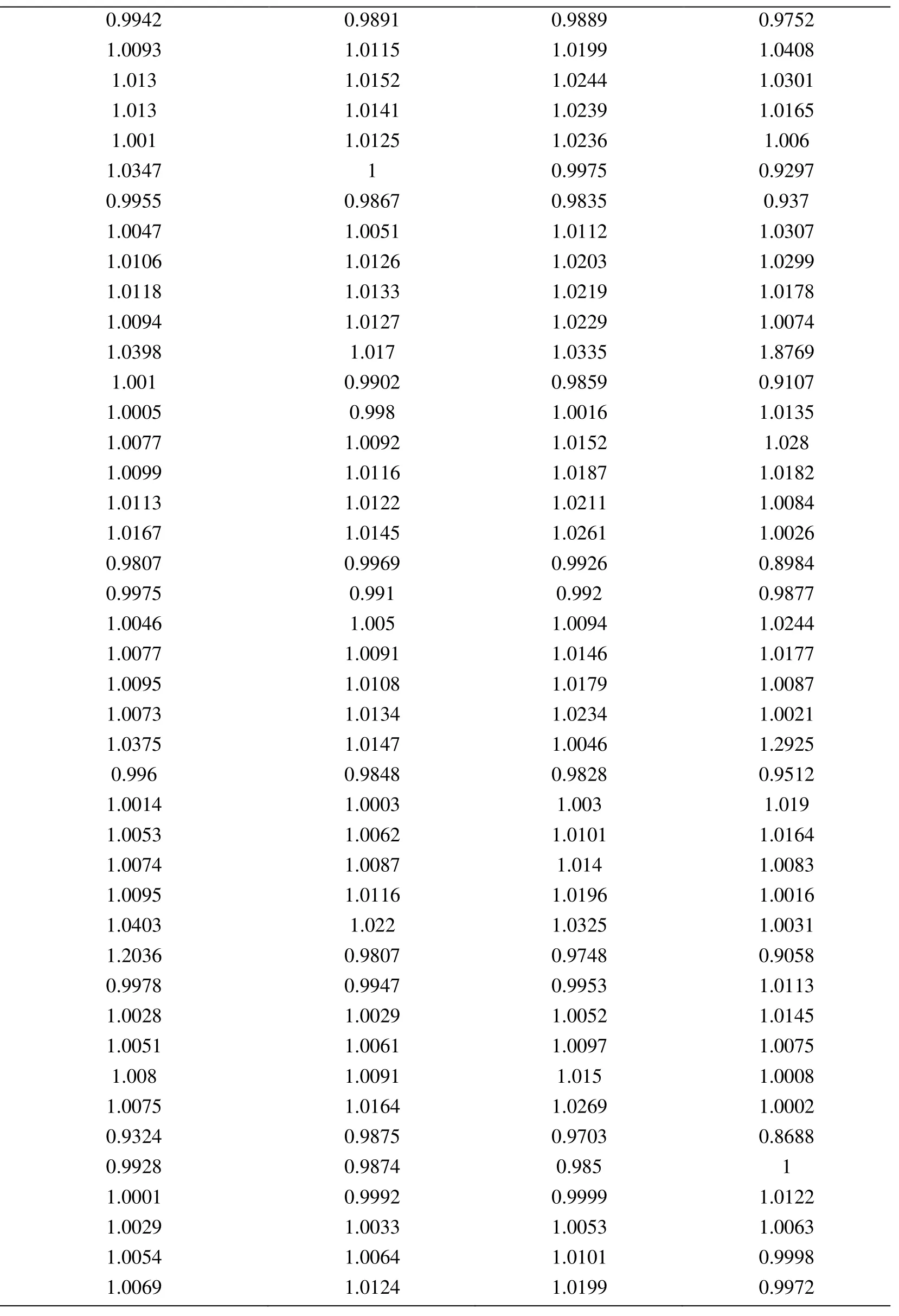
0.9942 0.9891 0.9889 0.9752 1.0093 1.0115 1.0199 1.0408 1.013 1.0152 1.0244 1.0301 1.013 1.0141 1.0239 1.0165 1.001 1.0125 1.0236 1.006 1.0347 1 0.9975 0.9297 0.9955 0.9867 0.9835 0.937 1.0047 1.0051 1.0112 1.0307 1.0106 1.0126 1.0203 1.0299 1.0118 1.0133 1.0219 1.0178 1.0094 1.0127 1.0229 1.0074 1.0398 1.017 1.0335 1.8769 1.001 0.9902 0.9859 0.9107 1.0005 0.998 1.0016 1.0135 1.0077 1.0092 1.0152 1.028 1.0099 1.0116 1.0187 1.0182 1.0113 1.0122 1.0211 1.0084 1.0167 1.0145 1.0261 1.0026 0.9807 0.9969 0.9926 0.8984 0.9975 0.991 0.992 0.9877 1.0046 1.005 1.0094 1.0244 1.0077 1.0091 1.0146 1.0177 1.0095 1.0108 1.0179 1.0087 1.0073 1.0134 1.0234 1.0021 1.0375 1.0147 1.0046 1.2925 0.996 0.9848 0.9828 0.9512 1.0014 1.0003 1.003 1.019 1.0053 1.0062 1.0101 1.0164 1.0074 1.0087 1.014 1.0083 1.0095 1.0116 1.0196 1.0016 1.0403 1.022 1.0325 1.0031 1.2036 0.9807 0.9748 0.9058 0.9978 0.9947 0.9953 1.0113 1.0028 1.0029 1.0052 1.0145 1.0051 1.0061 1.0097 1.0075 1.008 1.0091 1.015 1.0008 1.0075 1.0164 1.0269 1.0002 0.9324 0.9875 0.9703 0.8688 0.9928 0.9874 0.985 1 1.0001 0.9992 0.9999 1.0122 1.0029 1.0033 1.0053 1.0063 1.0054 1.0064 1.0101 0.9998 1.0069 1.0124 1.0199 0.9972

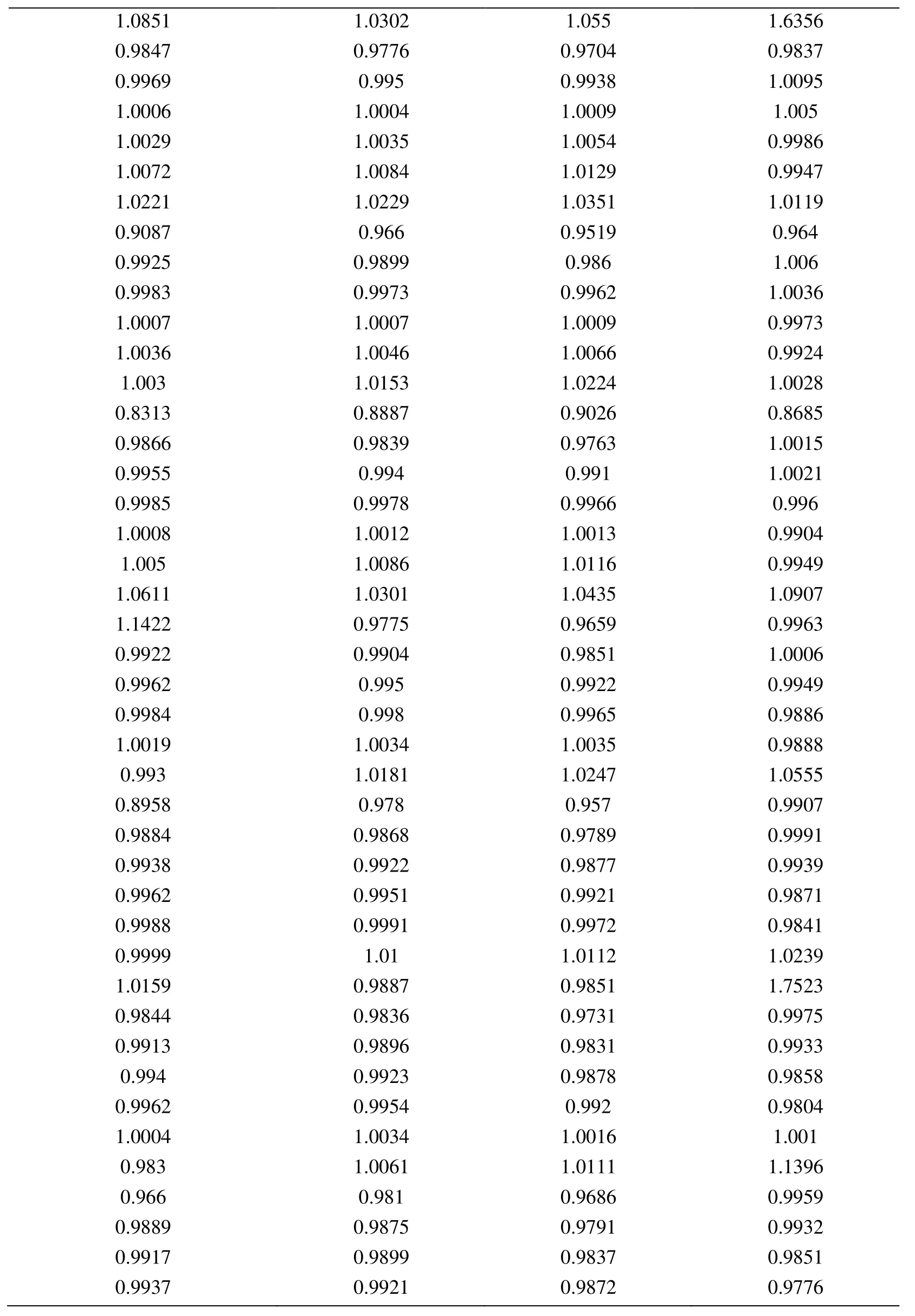
1.0851 1.0302 1.055 1.6356 0.9847 0.9776 0.9704 0.9837 0.9969 0.995 0.9938 1.0095 1.0006 1.0004 1.0009 1.005 1.0029 1.0035 1.0054 0.9986 1.0072 1.0084 1.0129 0.9947 1.0221 1.0229 1.0351 1.0119 0.9087 0.966 0.9519 0.964 0.9925 0.9899 0.986 1.006 0.9983 0.9973 0.9962 1.0036 1.0007 1.0007 1.0009 0.9973 1.0036 1.0046 1.0066 0.9924 1.003 1.0153 1.0224 1.0028 0.8313 0.8887 0.9026 0.8685 0.9866 0.9839 0.9763 1.0015 0.9955 0.994 0.991 1.0021 0.9985 0.9978 0.9966 0.996 1.0008 1.0012 1.0013 0.9904 1.005 1.0086 1.0116 0.9949 1.0611 1.0301 1.0435 1.0907 1.1422 0.9775 0.9659 0.9963 0.9922 0.9904 0.9851 1.0006 0.9962 0.995 0.9922 0.9949 0.9984 0.998 0.9965 0.9886 1.0019 1.0034 1.0035 0.9888 0.993 1.0181 1.0247 1.0555 0.8958 0.978 0.957 0.9907 0.9884 0.9868 0.9789 0.9991 0.9938 0.9922 0.9877 0.9939 0.9962 0.9951 0.9921 0.9871 0.9988 0.9991 0.9972 0.9841 0.9999 1.01 1.0112 1.0239 1.0159 0.9887 0.9851 1.7523 0.9844 0.9836 0.9731 0.9975 0.9913 0.9896 0.9831 0.9933 0.994 0.9923 0.9878 0.9858 0.9962 0.9954 0.992 0.9804 1.0004 1.0034 1.0016 1.001 0.983 1.0061 1.0111 1.1396 0.966 0.981 0.9686 0.9959 0.9889 0.9875 0.9791 0.9932 0.9917 0.9899 0.9837 0.9851 0.9937 0.9921 0.9872 0.9776

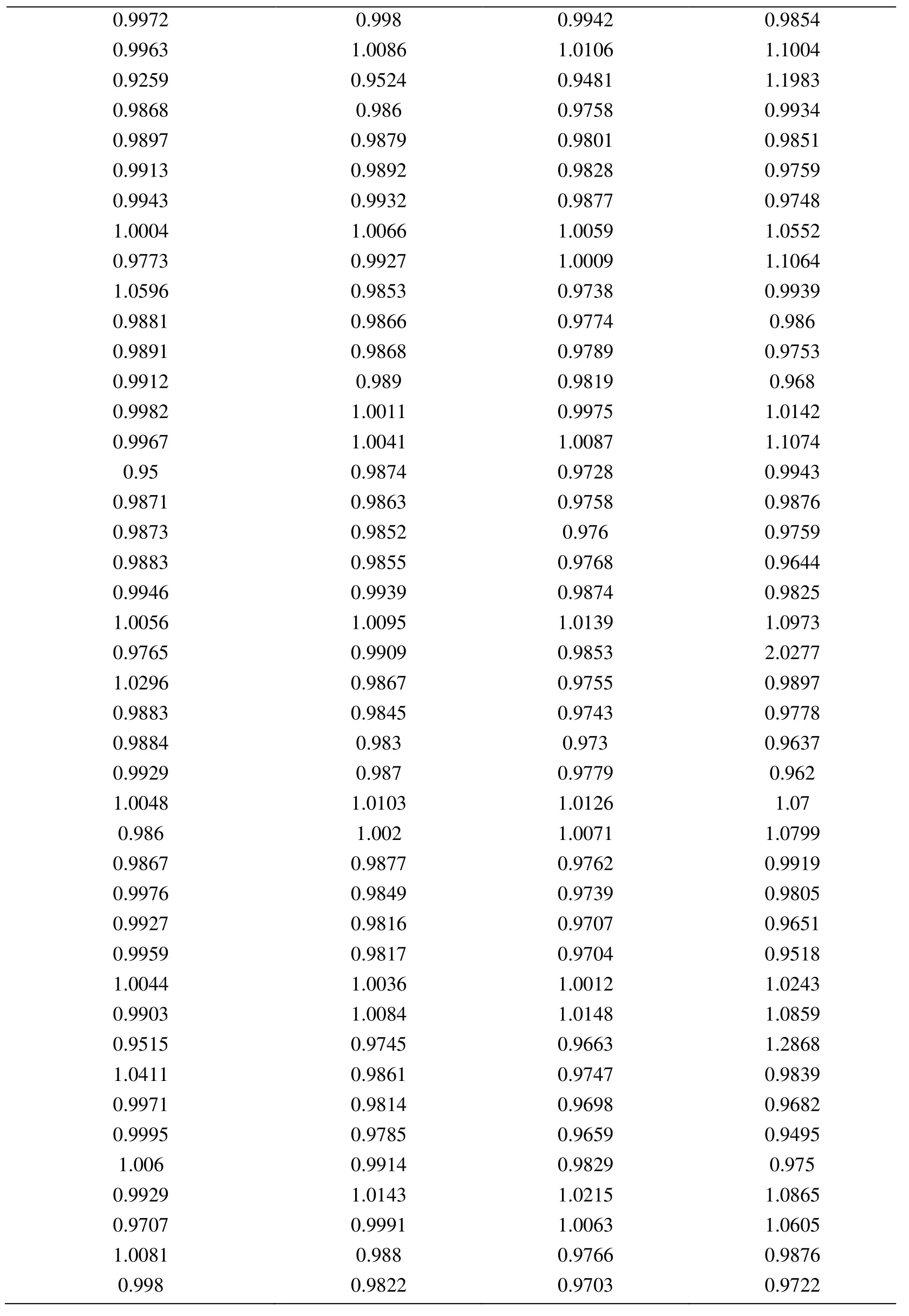
0.9972 0.998 0.9942 0.9854 0.9963 1.0086 1.0106 1.1004 0.9259 0.9524 0.9481 1.1983 0.9868 0.986 0.9758 0.9934 0.9897 0.9879 0.9801 0.9851 0.9913 0.9892 0.9828 0.9759 0.9943 0.9932 0.9877 0.9748 1.0004 1.0066 1.0059 1.0552 0.9773 0.9927 1.0009 1.1064 1.0596 0.9853 0.9738 0.9939 0.9881 0.9866 0.9774 0.986 0.9891 0.9868 0.9789 0.9753 0.9912 0.989 0.9819 0.968 0.9982 1.0011 0.9975 1.0142 0.9967 1.0041 1.0087 1.1074 0.95 0.9874 0.9728 0.9943 0.9871 0.9863 0.9758 0.9876 0.9873 0.9852 0.976 0.9759 0.9883 0.9855 0.9768 0.9644 0.9946 0.9939 0.9874 0.9825 1.0056 1.0095 1.0139 1.0973 0.9765 0.9909 0.9853 2.0277 1.0296 0.9867 0.9755 0.9897 0.9883 0.9845 0.9743 0.9778 0.9884 0.983 0.973 0.9637 0.9929 0.987 0.9779 0.962 1.0048 1.0103 1.0126 1.07 0.986 1.002 1.0071 1.0799 0.9867 0.9877 0.9762 0.9919 0.9976 0.9849 0.9739 0.9805 0.9927 0.9816 0.9707 0.9651 0.9959 0.9817 0.9704 0.9518 1.0044 1.0036 1.0012 1.0243 0.9903 1.0084 1.0148 1.0859 0.9515 0.9745 0.9663 1.2868 1.0411 0.9861 0.9747 0.9839 0.9971 0.9814 0.9698 0.9682 0.9995 0.9785 0.9659 0.9495 1.006 0.9914 0.9829 0.975 0.9929 1.0143 1.0215 1.0865 0.9707 0.9991 1.0063 1.0605 1.0081 0.988 0.9766 0.9876 0.998 0.9822 0.9703 0.9722

0.9989 0.9773 0.964 0.9521 1.0044 0.9804 0.967 0.9433 0.9958 1.0167 1.0222 1.0714 0.9816 1.0068 1.0132 1.0678 0.9719 0.9919 0.9793 0.9913 1.0025 0.9837 0.9719 0.9766 0.983 0.9774 0.9642 0.9569 0.9798 0.9743 0.9586 0.9333 0.9961 1.0088 1.0078 1.0251 1.0073 1.013 1.0209 1.0748 0.9724 0.9984 0.9962 2.0099 0.943 0.9859 0.9744 0.9812 0.9572 0.9786 0.9656 0.9625 0.942 0.9725 0.9564 0.9361 0.9619 0.9899 0.9785 0.9592 1.038 1.0197 1.0286 1.0784 1.0295 1.0056 1.0115 1.0545 0.9285 0.9903 0.9778 0.9861 0.95 0.9832 0.9678 0.9681 0.9189 0.9784 0.9576 0.9435 0.9119 0.9826 0.9563 0.9214 1.0718 1.0191 1.0309 1.0667 1.0881 1.0058 1.0183 1.0615 0.9627 1.0077 0.9644 1.6694 0.9147 0.9497 0.9388 1.0314 0.9135 0.9293 0.9258 0.9295 0.8867 0.8994 0.9131 0.8029 1.0479 1.0057 1.0064 1.1029 1.0918 1.054 1.0233 1.1683 1.0501 1.0309 1.0009 1.0681 1.1614 1.0381 1.0081 1.1036 1.1673 1.0611 1.034 1.2069 0.9322 0.9226 0.9438 0.8767 0.8456 0.9117 0.9167 0.8524 0.8857 0.9385 0.9313 0.9736 0.8843 0.9566 0.9439 1.0666 1.0373 1.0041 1.0095 1.0474 1.1237 1.0114 1.026 1.072 1.0367 1.0099 1.0049 1.0057 0.8437 0.9777 0.9522 0.9242 0.8829 0.9801 0.9619 0.9547 0.908 0.9856 0.9715 0.9756 0.9696 0.9877 0.9752 1.3226

1.0572 1.0105 1.0178 1.065 0.9328 1.0204 1.0263 1.0629 0.8925 0.9748 0.9579 0.9268 0.9484 0.9746 0.96 0.9478 0.9675 0.9813 0.9691 0.9706 0.9743 0.9894 0.9782 0.9877 1.0082 1.005 1.0108 1.0578 0.9435 1.0186 1.0269 1.0807 1.321 0.9871 0.9754 0.9565 1.2421 0.9745 0.9597 0.9419 1.1634 0.9798 0.9673 0.9655 0.9978 0.9865 0.9751 0.9831 0.9787 0.9972 0.9946 2.0152 1.0188 1.0125 1.0201 1.0796 1.0044 1.0037 1.0007 1.0141 0.9809 0.9764 0.9622 0.9401 0.9814 0.979 0.9665 0.9608 1.0022 0.9845 0.9729 0.9788 0.9595 0.9912 0.9783 0.9919 0.9645 1.0062 1.0124 1.0731 1.0095 1.0134 1.017 1.065 0.9858 0.9816 0.9694 0.9481 0.9823 0.9792 0.9671 0.957 0.9846 0.9832 0.9718 0.9749 0.9989 0.9878 0.9764 0.9889 0.979 0.9979 1.0052 1.0657 0.9726 1.0131 1.0191 1.0886 0.9927 0.9903 0.9817 0.972 0.9842 0.9808 0.9695 0.9555 0.9848 0.9828 0.9719 0.9716 1.0399 0.9863 0.9751 0.9858 0.9785 0.9714 0.9637 1.2748 0.9138 1.008 1.0139 1.0933 0.9991 1.0004 0.9964 1.0121 0.9872 0.9839 0.974 0.9577 0.9858 0.9834 0.9733 0.9694 0.9886 0.9855 0.9749 0.983 1.0342 0.9868 0.9751 0.9928 1.0268 1.0012 1.0061 1.0892 1.0017 1.0075 1.0077 1.0578 0.9908 0.9885 0.9804 0.9654 0.9877 0.985 0.9762 0.9685 0.9873 0.9856 0.976 0.9808

0.9917 0.9863 0.9753 0.9912 0.9693 0.9888 0.9821 2.0232 0.999 1.0087 1.0115 1.0954 0.9946 0.9941 0.9881 0.98 0.9901 0.9876 0.9802 0.9696 0.9887 0.9867 0.9783 0.9796 0.9899 0.9865 0.9764 0.9898 0.9624 0.9862 0.9708 0.9947 1.0915 1.0043 1.0084 1.1177 0.9977 1.0002 0.9964 1.0029 0.9928 0.9909 0.985 0.9725 0.9907 0.9886 0.9817 0.9794 0.9889 0.9874 0.9788 0.9888 0.9856 0.9842 0.9727 0.9951 0.9743 0.9927 1.0015 1.1249 0.9991 1.0057 1.0043 1.0355 0.9955 0.9948 0.9904 0.9775 0.9929 0.9911 0.9857 0.9802 0.9909 0.9891 0.9822 0.9885 0.9923 0.9857 0.9759 0.9954 0.9381 0.9444 0.9419 1.1654 0.9994 1.0108 1.0127 1.0798 0.9983 0.9991 0.9963 0.9847 0.9952 0.9939 0.9901 0.9819 0.9931 0.9914 0.9862 0.9888 0.9903 0.9879 0.9801 0.9958 0.9634 0.9788 0.966 0.9959 0.8511 1.0137 1.0205 1.1295 1.0016 1.0042 1.0036 0.9949 0.9976 0.9971 0.9948 0.9841 0.9954 0.994 0.9905 0.9897 0.9923 0.9906 0.9851 0.9965 0.9928 0.9825 0.9723 0.9987 1.1322 1.0025 1.0097 1.5155 1.0063 1.0109 1.0136 1.0092 1.0002 1.0006 0.9999 0.9868 0.9976 0.9968 0.9948 0.991 0.9951 0.9936 0.99 0.9974 0.9929 0.9869 0.9798 1.0014 0.9198 0.9749 0.9514 0.9836 1.0834 1.0199 1.0281 1.0285 1.0033 1.0046 1.006 0.9901 0.9998 0.9997 0.9992 0.9924

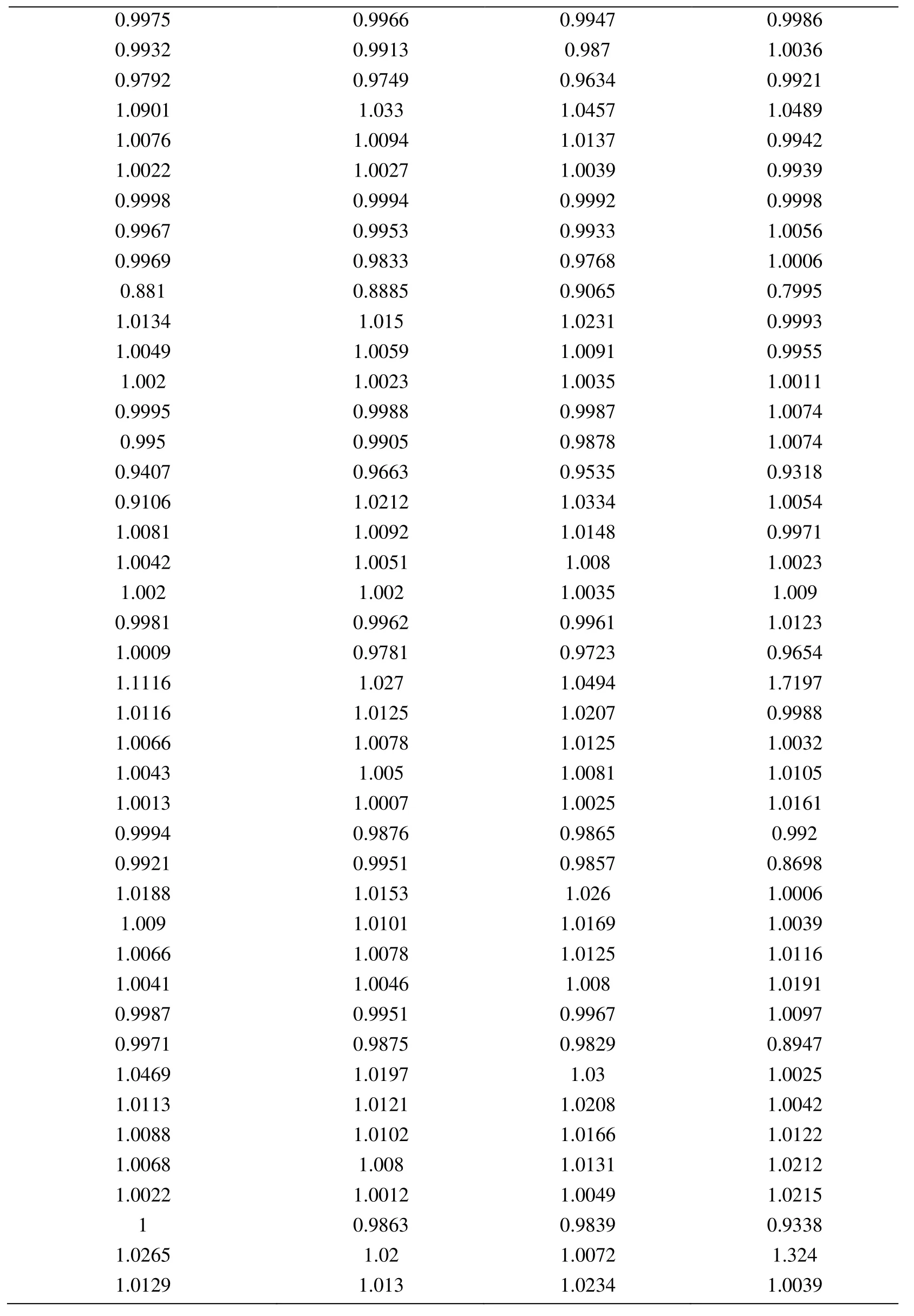
0.9975 0.9966 0.9947 0.9986 0.9932 0.9913 0.987 1.0036 0.9792 0.9749 0.9634 0.9921 1.0901 1.033 1.0457 1.0489 1.0076 1.0094 1.0137 0.9942 1.0022 1.0027 1.0039 0.9939 0.9998 0.9994 0.9992 0.9998 0.9967 0.9953 0.9933 1.0056 0.9969 0.9833 0.9768 1.0006 0.881 0.8885 0.9065 0.7995 1.0134 1.015 1.0231 0.9993 1.0049 1.0059 1.0091 0.9955 1.002 1.0023 1.0035 1.0011 0.9995 0.9988 0.9987 1.0074 0.995 0.9905 0.9878 1.0074 0.9407 0.9663 0.9535 0.9318 0.9106 1.0212 1.0334 1.0054 1.0081 1.0092 1.0148 0.9971 1.0042 1.0051 1.008 1.0023 1.002 1.002 1.0035 1.009 0.9981 0.9962 0.9961 1.0123 1.0009 0.9781 0.9723 0.9654 1.1116 1.027 1.0494 1.7197 1.0116 1.0125 1.0207 0.9988 1.0066 1.0078 1.0125 1.0032 1.0043 1.005 1.0081 1.0105 1.0013 1.0007 1.0025 1.0161 0.9994 0.9876 0.9865 0.992 0.9921 0.9951 0.9857 0.8698 1.0188 1.0153 1.026 1.0006 1.009 1.0101 1.0169 1.0039 1.0066 1.0078 1.0125 1.0116 1.0041 1.0046 1.008 1.0191 0.9987 0.9951 0.9967 1.0097 0.9971 0.9875 0.9829 0.8947 1.0469 1.0197 1.03 1.0025 1.0113 1.0121 1.0208 1.0042 1.0088 1.0102 1.0166 1.0122 1.0068 1.008 1.0131 1.0212 1.0022 1.0012 1.0049 1.0215 1 0.9863 0.9839 0.9338 1.0265 1.02 1.0072 1.324 1.0129 1.013 1.0234 1.0039

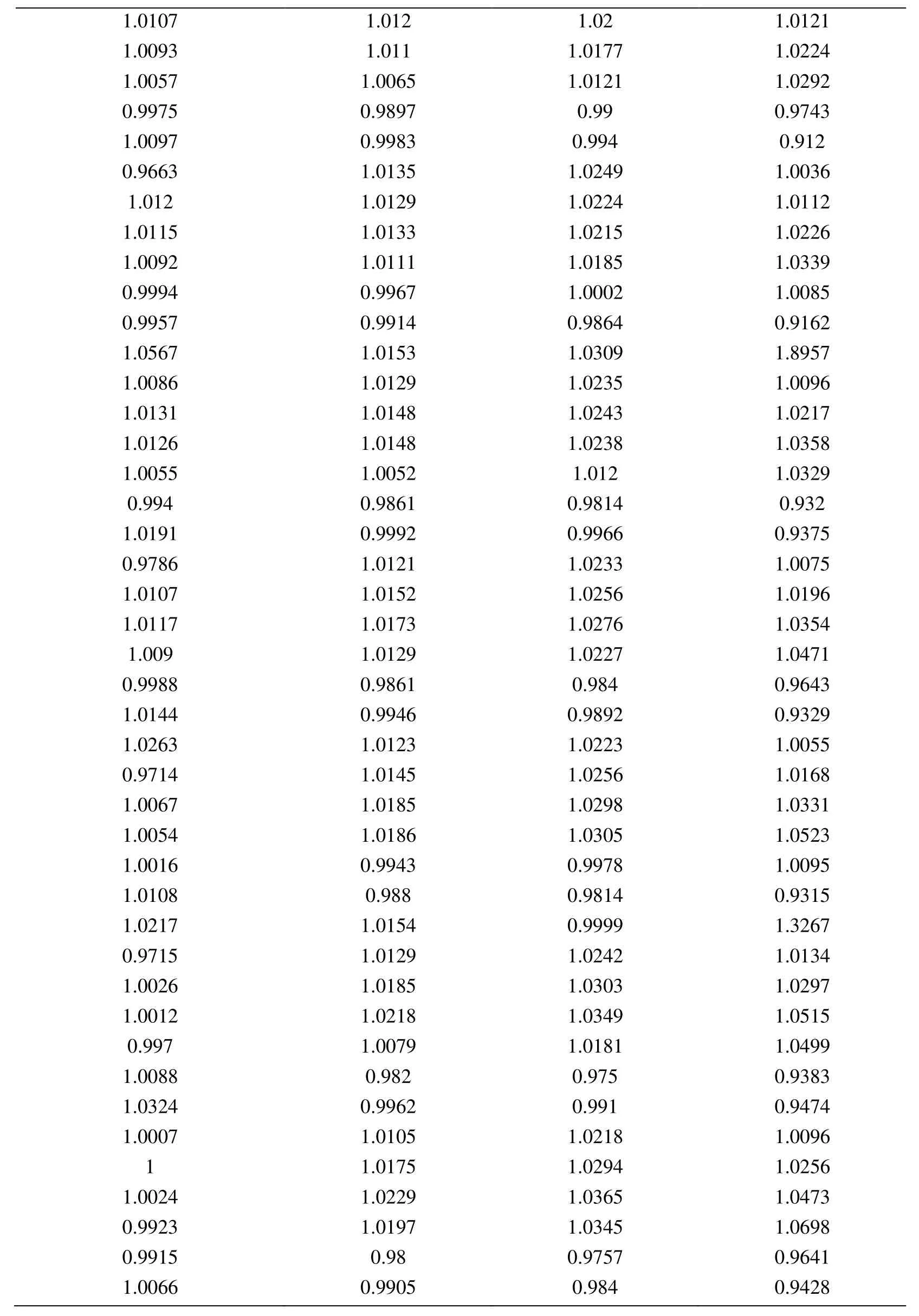
1.0107 1.012 1.02 1.0121 1.0093 1.011 1.0177 1.0224 1.0057 1.0065 1.0121 1.0292 0.9975 0.9897 0.99 0.9743 1.0097 0.9983 0.994 0.912 0.9663 1.0135 1.0249 1.0036 1.012 1.0129 1.0224 1.0112 1.0115 1.0133 1.0215 1.0226 1.0092 1.0111 1.0185 1.0339 0.9994 0.9967 1.0002 1.0085 0.9957 0.9914 0.9864 0.9162 1.0567 1.0153 1.0309 1.8957 1.0086 1.0129 1.0235 1.0096 1.0131 1.0148 1.0243 1.0217 1.0126 1.0148 1.0238 1.0358 1.0055 1.0052 1.012 1.0329 0.994 0.9861 0.9814 0.932 1.0191 0.9992 0.9966 0.9375 0.9786 1.0121 1.0233 1.0075 1.0107 1.0152 1.0256 1.0196 1.0117 1.0173 1.0276 1.0354 1.009 1.0129 1.0227 1.0471 0.9988 0.9861 0.984 0.9643 1.0144 0.9946 0.9892 0.9329 1.0263 1.0123 1.0223 1.0055 0.9714 1.0145 1.0256 1.0168 1.0067 1.0185 1.0298 1.0331 1.0054 1.0186 1.0305 1.0523 1.0016 0.9943 0.9978 1.0095 1.0108 0.988 0.9814 0.9315 1.0217 1.0154 0.9999 1.3267 0.9715 1.0129 1.0242 1.0134 1.0026 1.0185 1.0303 1.0297 1.0012 1.0218 1.0349 1.0515 0.997 1.0079 1.0181 1.0499 1.0088 0.982 0.975 0.9383 1.0324 0.9962 0.991 0.9474 1.0007 1.0105 1.0218 1.0096 1 1.0175 1.0294 1.0256 1.0024 1.0229 1.0365 1.0473 0.9923 1.0197 1.0345 1.0698 0.9915 0.98 0.9757 0.9641 1.0066 0.9905 0.984 0.9428

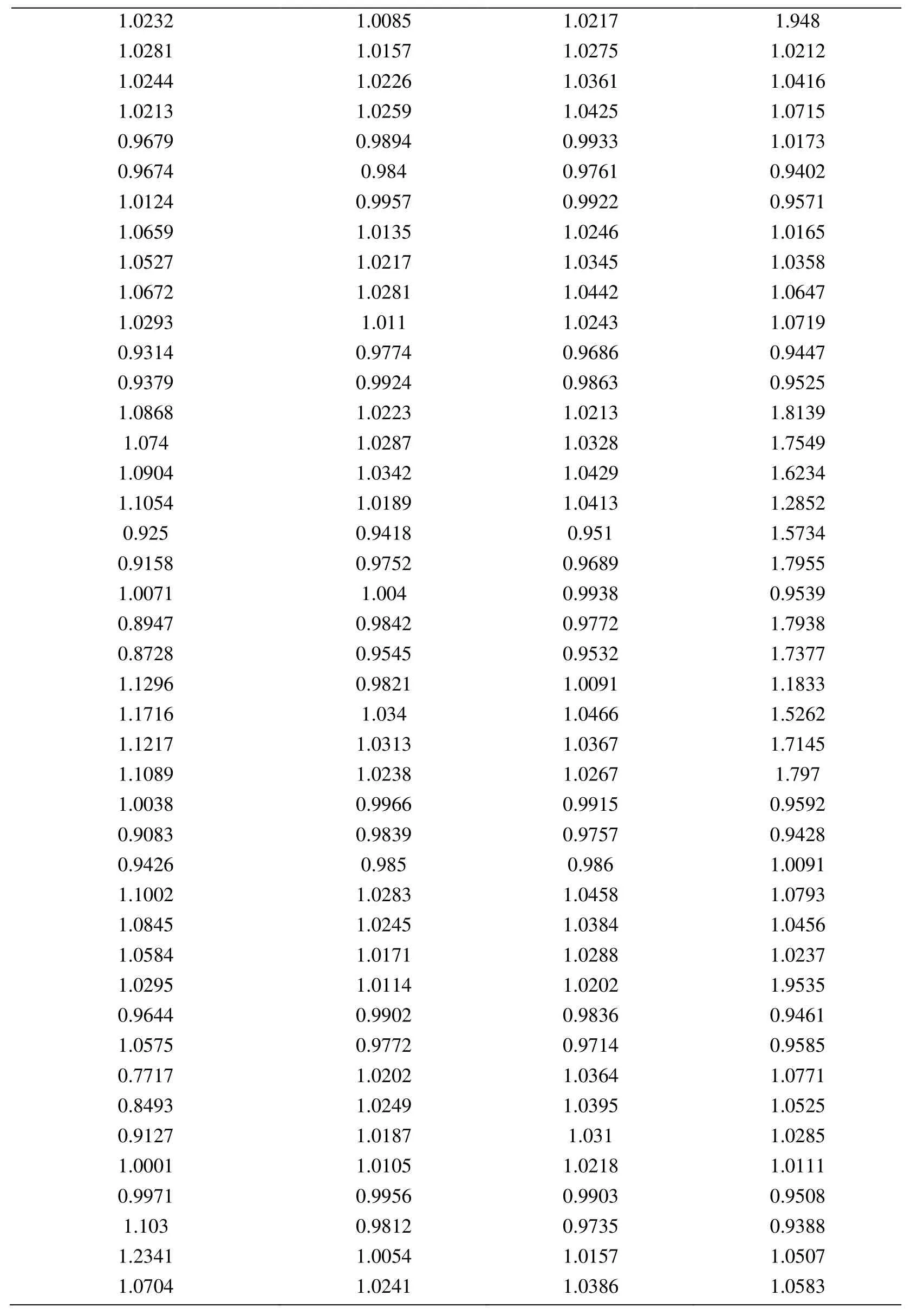
1.0232 1.0085 1.0217 1.948 1.0281 1.0157 1.0275 1.0212 1.0244 1.0226 1.0361 1.0416 1.0213 1.0259 1.0425 1.0715 0.9679 0.9894 0.9933 1.0173 0.9674 0.984 0.9761 0.9402 1.0124 0.9957 0.9922 0.9571 1.0659 1.0135 1.0246 1.0165 1.0527 1.0217 1.0345 1.0358 1.0672 1.0281 1.0442 1.0647 1.0293 1.011 1.0243 1.0719 0.9314 0.9774 0.9686 0.9447 0.9379 0.9924 0.9863 0.9525 1.0868 1.0223 1.0213 1.8139 1.074 1.0287 1.0328 1.7549 1.0904 1.0342 1.0429 1.6234 1.1054 1.0189 1.0413 1.2852 0.925 0.9418 0.951 1.5734 0.9158 0.9752 0.9689 1.7955 1.0071 1.004 0.9938 0.9539 0.8947 0.9842 0.9772 1.7938 0.8728 0.9545 0.9532 1.7377 1.1296 0.9821 1.0091 1.1833 1.1716 1.034 1.0466 1.5262 1.1217 1.0313 1.0367 1.7145 1.1089 1.0238 1.0267 1.797 1.0038 0.9966 0.9915 0.9592 0.9083 0.9839 0.9757 0.9428 0.9426 0.985 0.986 1.0091 1.1002 1.0283 1.0458 1.0793 1.0845 1.0245 1.0384 1.0456 1.0584 1.0171 1.0288 1.0237 1.0295 1.0114 1.0202 1.9535 0.9644 0.9902 0.9836 0.9461 1.0575 0.9772 0.9714 0.9585 0.7717 1.0202 1.0364 1.0771 0.8493 1.0249 1.0395 1.0525 0.9127 1.0187 1.031 1.0285 1.0001 1.0105 1.0218 1.0111 0.9971 0.9956 0.9903 0.9508 1.103 0.9812 0.9735 0.9388 1.2341 1.0054 1.0157 1.0507 1.0704 1.0241 1.0386 1.0583

1.0166 1.0199 1.0324 1.0333 1.0204 1.0134 1.0249 1.0155 1.0272 1.0138 0.9983 1.3207 1.0237 0.9878 0.9808 0.9356 0.9908 0.9899 0.9918 1.0011 1.0169 1.0207 1.0342 1.0601 1.0181 1.0203 1.0325 1.0377 0.9876 1.0153 1.0267 1.0194 1.029 1.0113 1.0213 1.0063 1.0761 0.9942 0.9885 0.9385 0.9882 0.9834 0.9794 0.9557 1.0109 1.014 1.0251 1.0535 1.0167 1.0194 1.031 1.0409 1.0151 1.0163 1.0274 1.0229 0.9625 1.0118 1.0231 1.0091 1.0296 0.9984 0.9956 0.9434 1.0427 0.9855 0.9797 0.9309 1.0034 1.0043 1.0115 1.0339 1.0142 1.017 1.0274 1.0421 1.0146 1.0163 1.0266 1.0256 0.9635 1.0132 1.024 1.0118 1.0056 1.0138 1.0287 1.9108 1.0556 0.9915 0.986 0.9226 0.9972 0.9943 0.997 1.0008 1.0108 1.0131 1.0219 1.0402 1.0132 1.0152 1.0244 1.0272 1.0126 1.0137 1.0237 1.014 1.0064 1.0126 1.024 1.0047 0.9941 0.9984 0.9939 0.923 0.9952 0.988 0.9869 0.9609 1.0067 1.0079 1.0146 1.0341 1.011 1.013 1.0209 1.0275 1.0119 1.0132 1.0221 1.0155 1.0079 1.0128 1.0234 1.0058 1.0434 1.021 1.0069 1.3359 0.9981 0.9875 0.9841 0.924 1.0026 1.0016 1.0062 1.0229 1.0083 1.01 1.0162 1.0264 1.0102 1.0118 1.0191 1.0161 1.0105 1.0124 1.0217 1.0067 1.0317 1.0178 1.0279 1.0026 1.0663 0.9922 0.9878 0.8985 0.999 0.9948 0.9971 1.0053

1.0055 1.0063 1.0109 1.0239 1.0081 1.0095 1.0153 1.0158 1.01 1.0111 1.0187 1.007 1.0081 1.0144 1.0253 1.0017 1.0206 0.9995 0.9944 0.8874 0.996 0.9877 0.9872 0.9788 1.0025 1.0021 1.0051 1.02 1.0057 1.0068 1.0109 1.0148 1.0079 1.0091 1.0149 1.0068 1.0083 1.0127 1.0215 1.0009 1.0605 1.0239 1.0444 1.7788 0.9932 0.9805 0.9762 0.9408 0.9992 0.9972 0.9983 1.0147 1.0033 1.0037 1.0063 1.0133 1.0056 1.0066 1.0106 1.006 1.009 1.01 1.0166 0.9998 1.0205 1.0189 1.0308 1.0021 0.9072 0.9741 0.9643 0.896 0.995 0.9911 0.9897 1.0072 1.0008 1.0003 1.0013 1.0114 1.0033 1.0039 1.0062 1.005 1.0061 1.0072 1.0114 0.9987 1.0056 1.0146 1.0234 0.9984 0.8928 0.9185 0.9327 0.8883 0.9884 0.983 0.9777 0.9965 0.998 0.9966 0.9958 1.0092 1.0011 1.0011 1.0018 1.0037 1.0035 1.0042 1.0065 0.9974 1.0073 1.0101 1.0155 0.9951 1.0608 1.0317 1.0437 1.0244 1.2106 0.9726 0.9616 0.9823 0.9943 0.9922 0.9891 1.0065 0.9988 0.9981 0.9973 1.0024 1.0011 1.0013 1.0018 0.9961 1.0046 1.0059 1.0085 0.9923 1.0026 1.0195 1.0288 1.0122 0.8525 0.9719 0.9456 0.9683 0.9894 0.987 0.9808 1.0032 0.9963 0.995 0.9924 1.001 0.9989 0.9984 0.9974 0.9948 1.0015 1.0021 1.0026 0.9898 1.0034 1.0116 1.0158 1.0009 1.1051 1.0229 1.0429 1.3416

0.9835 0.9815 0.9717 0.9995 0.9934 0.9917 0.9871 0.9997 0.9967 0.9956 0.9931 0.9935 0.9989 0.9988 0.9975 0.9877 1.0034 1.0053 1.006 0.9921 1.005 1.0213 1.0307 1.0951 0.9515 0.9761 0.9628 0.9948 0.99 0.9884 0.9814 0.9985 0.9944 0.9929 0.9887 0.9925 0.9966 0.9957 0.9929 0.9859 0.9996 1.0004 0.9989 0.9855 0.9959 1.013 1.0158 1.052 0.8977 0.9342 0.934 1.1211 0.9865 0.9853 0.9759 0.9974 0.992 0.9903 0.9843 0.9918 0.9944 0.9928 0.9886 0.9844 0.9968 0.9964 0.9931 0.9805 1.0006 1.0062 1.0052 1.0183 0.9873 0.9958 1.0057 1.1449 1.0815 0.9829 0.9714 0.9963 0.9897 0.9881 0.9802 0.9917 0.9921 0.9902 0.9844 0.9834 0.9942 0.9928 0.988 0.9768 0.9981 1.0003 0.997 0.9951 0.9891 1.0062 1.0097 1.1232 0.9354 0.9846 0.9683 0.995 0.9876 0.9866 0.977 0.992 0.99 0.9881 0.9807 0.9832 0.9917 0.9896 0.9834 0.9743 0.9953 0.995 0.9898 0.9794 1.0005 1.0082 1.0095 1.0859 0.9746 0.9865 0.9787 2.0093 0.9862 0.9859 0.9749 0.9928 0.9883 0.9867 0.9777 0.9839 0.9894 0.987 0.9793 0.9732 0.9921 0.9901 0.9832 0.9691 1.0001 1.0051 1.0035 1.0421 0.9865 1.0005 1.0051 1.101 0.9776 0.9857 0.9739 0.9937 0.9872 0.9861 0.9759 0.9854 0.9874 0.9851 0.976 0.9735 0.9889 0.9861 0.9775 0.9632 0.9971 0.9982 0.9933 1.0014

1.0046 1.0073 1.0124 1.1006 0.9302 0.9679 0.9607 1.2608 1.0165 0.9864 0.9754 0.9876 0.9882 0.9841 0.9739 0.975 0.9887 0.983 0.973 0.961 0.9951 0.9901 0.9819 0.9708 1.0054 1.0116 1.0161 1.088 0.9808 0.9966 1.004 1.0722 1.0395 0.9874 0.976 0.9902 0.9927 0.9841 0.9732 0.9777 0.993 0.9812 0.9701 0.9618 0.9974 0.9832 0.9723 0.9532 1.0038 1.0097 1.0111 1.0551 0.9828 1.0055 1.0115 1.0795 0.9678 0.9905 0.9772 0.9925 1.0328 0.9851 0.9738 0.981 0.9973 0.9806 0.9689 0.9646 1.0006 0.9787 0.9659 0.9467 1.0056 0.9995 0.9947 1.0034 0.989 1.0119 1.0191 1.0847 0.9804 0.996 0.9927 2.0201 1.0075 0.9869 0.9755 0.9848 0.9979 0.9811 0.9691 0.9686 0.9995 0.9766 0.963 0.9476 1.0055 0.9857 0.9742 0.9559 0.9926 1.0172 1.0246 1.0819 0.9738 1.0043 1.01 1.0618 0.9805 0.9894 0.9781 0.9889 1.001 0.9824 0.9704 0.9731 0.9822 0.9763 0.9626 0.9521 0.9802 0.9759 0.9604 0.9329 1.0005 1.0165 1.0206 1.0568 1.0063 1.0101 1.0173 1.0691 0.9697 0.9817 0.9729 1.3151 0.949 0.9843 0.9726 0.9778 0.9545 0.9772 0.9638 0.958 0.9391 0.972 0.9553 0.9305 0.9863 1.0026 0.9973 0.9961 1.0431 1.0167 1.0253 1.0756 1.004 1.0019 1.0089 1.0499 0.931 0.9885 0.9756 0.9826 0.9367 0.9821 0.9659 0.964 0.9138 0.9777 0.9554 0.9371

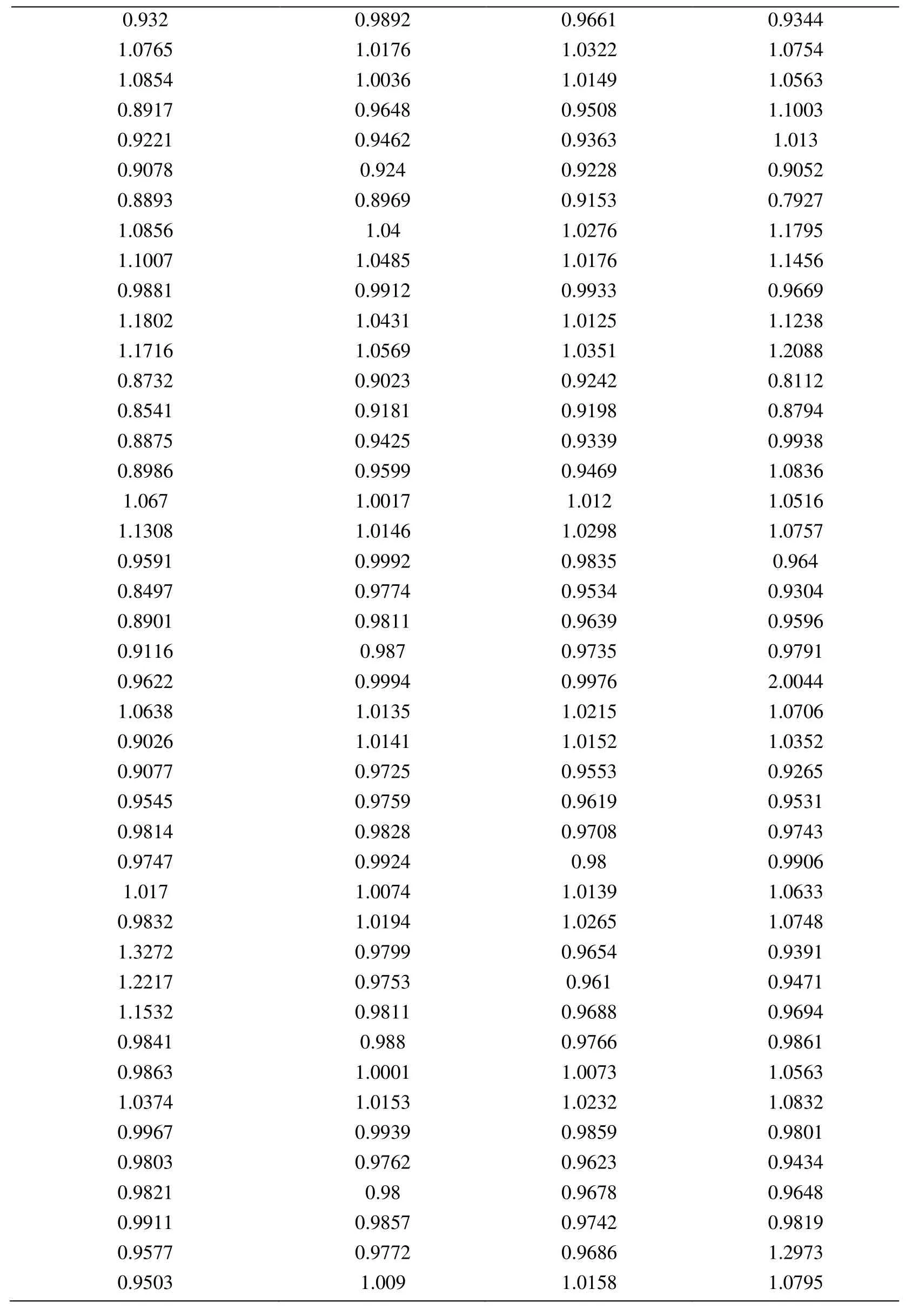
0.932 0.9892 0.9661 0.9344 1.0765 1.0176 1.0322 1.0754 1.0854 1.0036 1.0149 1.0563 0.8917 0.9648 0.9508 1.1003 0.9221 0.9462 0.9363 1.013 0.9078 0.924 0.9228 0.9052 0.8893 0.8969 0.9153 0.7927 1.0856 1.04 1.0276 1.1795 1.1007 1.0485 1.0176 1.1456 0.9881 0.9912 0.9933 0.9669 1.1802 1.0431 1.0125 1.1238 1.1716 1.0569 1.0351 1.2088 0.8732 0.9023 0.9242 0.8112 0.8541 0.9181 0.9198 0.8794 0.8875 0.9425 0.9339 0.9938 0.8986 0.9599 0.9469 1.0836 1.067 1.0017 1.012 1.0516 1.1308 1.0146 1.0298 1.0757 0.9591 0.9992 0.9835 0.964 0.8497 0.9774 0.9534 0.9304 0.8901 0.9811 0.9639 0.9596 0.9116 0.987 0.9735 0.9791 0.9622 0.9994 0.9976 2.0044 1.0638 1.0135 1.0215 1.0706 0.9026 1.0141 1.0152 1.0352 0.9077 0.9725 0.9553 0.9265 0.9545 0.9759 0.9619 0.9531 0.9814 0.9828 0.9708 0.9743 0.9747 0.9924 0.98 0.9906 1.017 1.0074 1.0139 1.0633 0.9832 1.0194 1.0265 1.0748 1.3272 0.9799 0.9654 0.9391 1.2217 0.9753 0.961 0.9471 1.1532 0.9811 0.9688 0.9694 0.9841 0.988 0.9766 0.9861 0.9863 1.0001 1.0073 1.0563 1.0374 1.0153 1.0232 1.0832 0.9967 0.9939 0.9859 0.9801 0.9803 0.9762 0.9623 0.9434 0.9821 0.98 0.9678 0.9648 0.9911 0.9857 0.9742 0.9819 0.9577 0.9772 0.9686 1.2973 0.9503 1.009 1.0158 1.0795

1.0061 1.0077 1.0074 1.0368 0.9838 0.9795 0.9669 0.9457 0.9826 0.9799 0.9679 0.9609 0.9959 0.9841 0.9728 0.9781 0.9841 0.9884 0.977 0.9909 0.9839 1.0028 1.0082 1.0725 1.0084 1.013 1.0174 1.0777 0.9892 0.9859 0.9757 0.959 0.984 0.9809 0.9697 0.9585 0.9851 0.9834 0.9725 0.9747 1.0535 0.9869 0.9757 0.9881 0.9722 0.9928 0.9881 2.0273 0.9546 1.0104 1.016 1.0946 0.9954 0.9946 0.9881 0.9872 0.9865 0.9833 0.9733 0.9589 0.9859 0.9837 0.9736 0.9722 0.9992 0.986 0.9752 0.9854 1.0165 0.9886 0.9745 0.9937 1.0598 1.0042 1.0095 1.0967 0.9998 1.0031 1.0006 1.0279 0.9897 0.987 0.9786 0.9633 0.9875 0.985 0.9761 0.971 0.9873 0.9858 0.976 0.9832 0.9872 0.9861 0.9747 0.9927 0.9714 0.9938 1.0016 1.0918 1.0001 1.008 1.0088 1.0719 0.9932 0.9918 0.9853 0.9726 0.9897 0.9872 0.9797 0.9712 0.9885 0.9866 0.978 0.9818 0.9915 0.9862 0.9757 0.9914 0.9538 0.9587 0.9532 1.2238 0.9957 1.0073 1.0103 1.1085 0.9964 0.9973 0.9926 0.9881 0.9922 0.9902 0.9841 0.9732 0.9903 0.9883 0.9812 0.9813 0.9891 0.987 0.978 0.9905 0.9715 0.9829 0.9707 0.9954 0.9662 1.0021 1.0063 1.1306 0.999 1.0031 1.0005 1.0113 0.9948 0.9937 0.9891 0.9767 0.9925 0.9906 0.9851 0.9818 0.9903 0.9886 0.9813 0.9901 0.9921 0.9845 0.9738 0.996

?

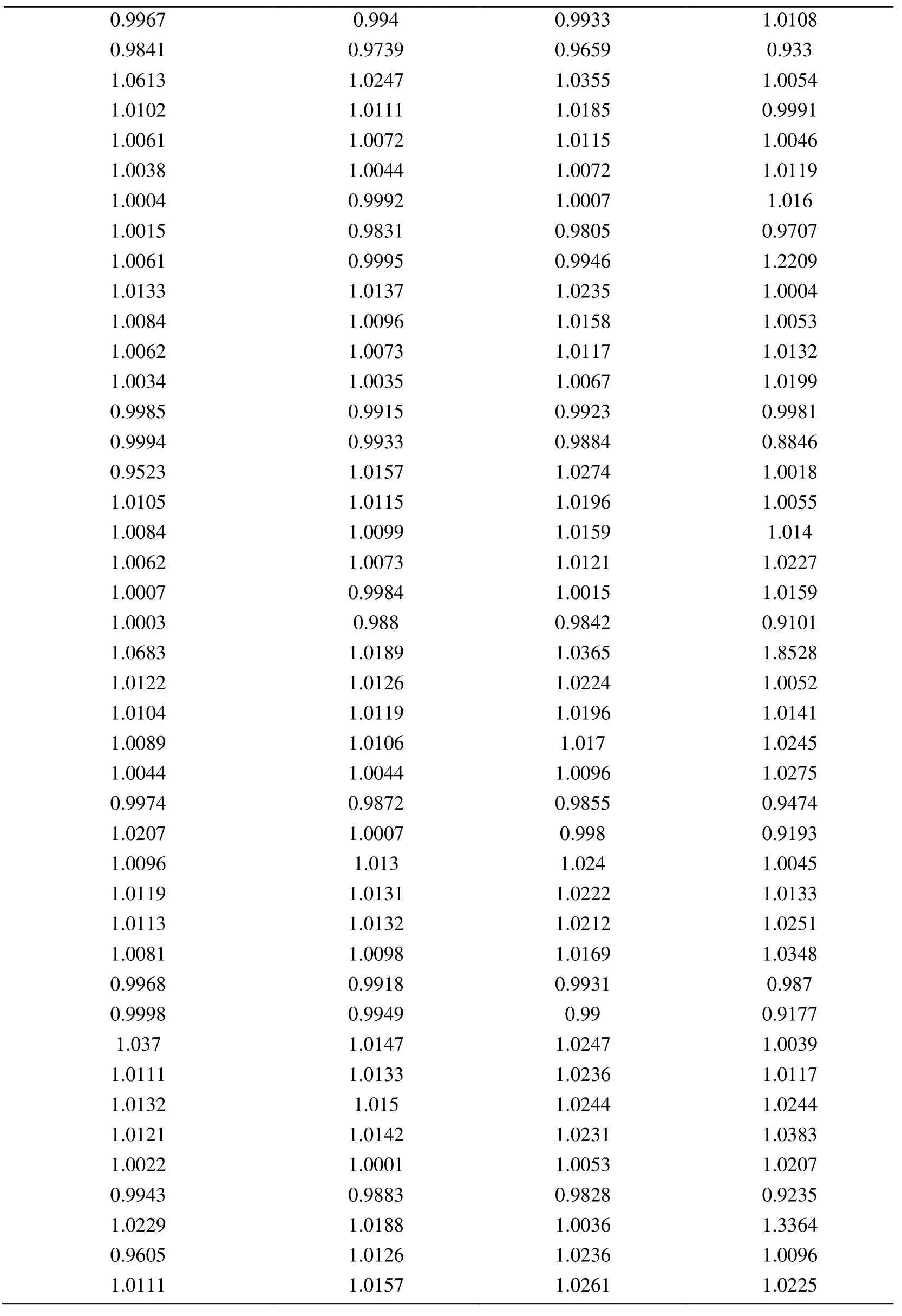
0.9967 0.994 0.9933 1.0108 0.9841 0.9739 0.9659 0.933 1.0613 1.0247 1.0355 1.0054 1.0102 1.0111 1.0185 0.9991 1.0061 1.0072 1.0115 1.0046 1.0038 1.0044 1.0072 1.0119 1.0004 0.9992 1.0007 1.016 1.0015 0.9831 0.9805 0.9707 1.0061 0.9995 0.9946 1.2209 1.0133 1.0137 1.0235 1.0004 1.0084 1.0096 1.0158 1.0053 1.0062 1.0073 1.0117 1.0132 1.0034 1.0035 1.0067 1.0199 0.9985 0.9915 0.9923 0.9981 0.9994 0.9933 0.9884 0.8846 0.9523 1.0157 1.0274 1.0018 1.0105 1.0115 1.0196 1.0055 1.0084 1.0099 1.0159 1.014 1.0062 1.0073 1.0121 1.0227 1.0007 0.9984 1.0015 1.0159 1.0003 0.988 0.9842 0.9101 1.0683 1.0189 1.0365 1.8528 1.0122 1.0126 1.0224 1.0052 1.0104 1.0119 1.0196 1.0141 1.0089 1.0106 1.017 1.0245 1.0044 1.0044 1.0096 1.0275 0.9974 0.9872 0.9855 0.9474 1.0207 1.0007 0.998 0.9193 1.0096 1.013 1.024 1.0045 1.0119 1.0131 1.0222 1.0133 1.0113 1.0132 1.0212 1.0251 1.0081 1.0098 1.0169 1.0348 0.9968 0.9918 0.9931 0.987 0.9998 0.9949 0.99 0.9177 1.037 1.0147 1.0247 1.0039 1.0111 1.0133 1.0236 1.0117 1.0132 1.015 1.0244 1.0244 1.0121 1.0142 1.0231 1.0383 1.0022 1.0001 1.0053 1.0207 0.9943 0.9883 0.9828 0.9235 1.0229 1.0188 1.0036 1.3364 0.9605 1.0126 1.0236 1.0096 1.0111 1.0157 1.0261 1.0225

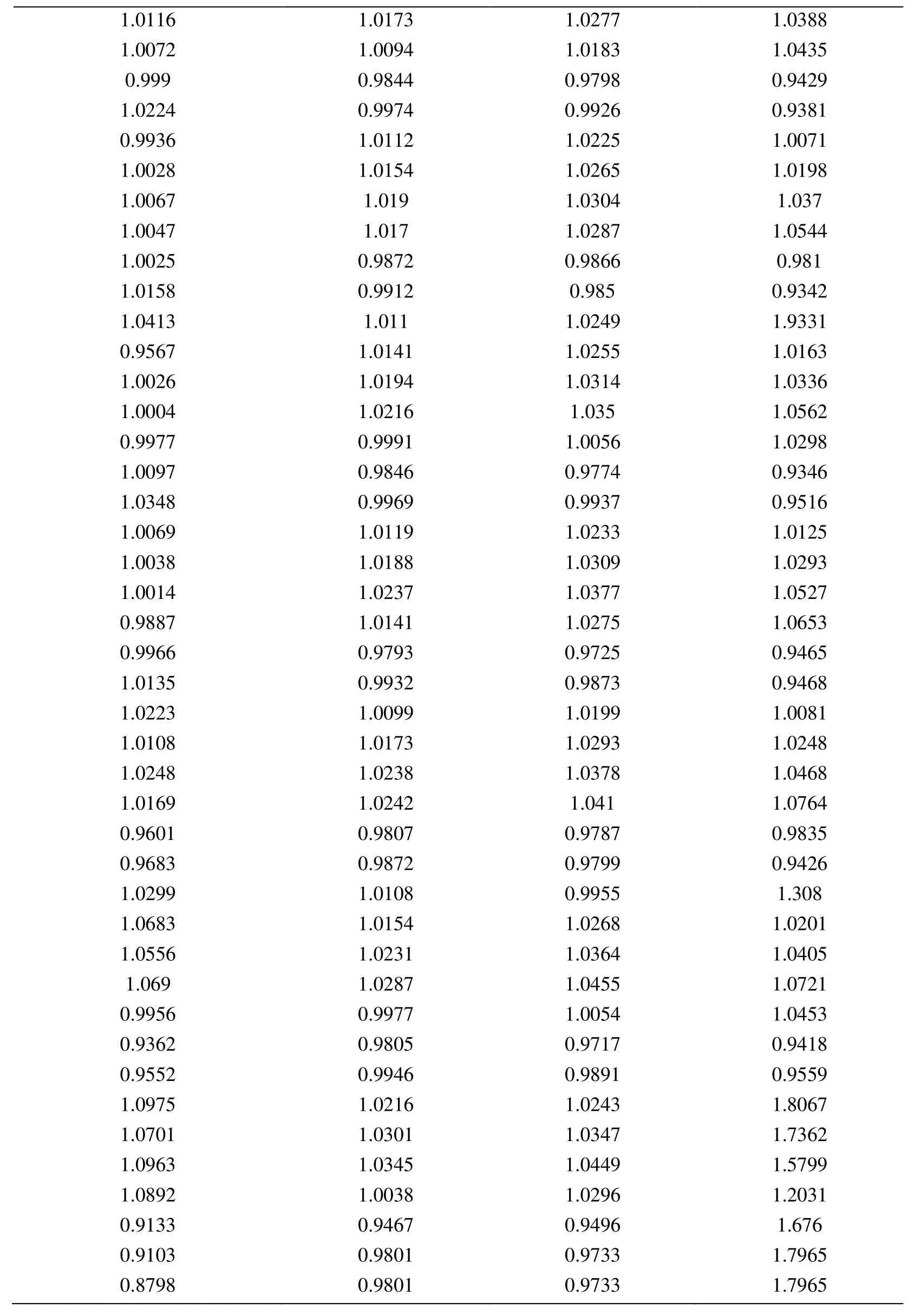
1.0116 1.0173 1.0277 1.0388 1.0072 1.0094 1.0183 1.0435 0.999 0.9844 0.9798 0.9429 1.0224 0.9974 0.9926 0.9381 0.9936 1.0112 1.0225 1.0071 1.0028 1.0154 1.0265 1.0198 1.0067 1.019 1.0304 1.037 1.0047 1.017 1.0287 1.0544 1.0025 0.9872 0.9866 0.981 1.0158 0.9912 0.985 0.9342 1.0413 1.011 1.0249 1.9331 0.9567 1.0141 1.0255 1.0163 1.0026 1.0194 1.0314 1.0336 1.0004 1.0216 1.035 1.0562 0.9977 0.9991 1.0056 1.0298 1.0097 0.9846 0.9774 0.9346 1.0348 0.9969 0.9937 0.9516 1.0069 1.0119 1.0233 1.0125 1.0038 1.0188 1.0309 1.0293 1.0014 1.0237 1.0377 1.0527 0.9887 1.0141 1.0275 1.0653 0.9966 0.9793 0.9725 0.9465 1.0135 0.9932 0.9873 0.9468 1.0223 1.0099 1.0199 1.0081 1.0108 1.0173 1.0293 1.0248 1.0248 1.0238 1.0378 1.0468 1.0169 1.0242 1.041 1.0764 0.9601 0.9807 0.9787 0.9835 0.9683 0.9872 0.9799 0.9426 1.0299 1.0108 0.9955 1.308 1.0683 1.0154 1.0268 1.0201 1.0556 1.0231 1.0364 1.0405 1.069 1.0287 1.0455 1.0721 0.9956 0.9977 1.0054 1.0453 0.9362 0.9805 0.9717 0.9418 0.9552 0.9946 0.9891 0.9559 1.0975 1.0216 1.0243 1.8067 1.0701 1.0301 1.0347 1.7362 1.0963 1.0345 1.0449 1.5799 1.0892 1.0038 1.0296 1.2031 0.9133 0.9467 0.9496 1.676 0.9103 0.9801 0.9733 1.7965 0.8798 0.9801 0.9733 1.7965

0.8807 0.9467 0.9496 1.676 1.1753 1.0038 1.0296 1.2031 1.16 1.0345 1.0449 1.5799 1.1153 1.0301 1.0347 1.7362 1.0899 1.0216 1.0243 1.8067 0.9621 0.9946 0.9891 0.9559 0.9037 0.9805 0.9717 0.9418 0.9951 0.9977 1.0054 1.0453 1.1001 1.0287 1.0455 1.0721 1.0803 1.0231 1.0364 1.0405 1.0575 1.0154 1.0268 1.0201 1.0525 1.0108 0.9955 1.308 0.9634 0.9872 0.9799 0.9426 1.0015 0.9807 0.9787 0.9835 0.778 1.0242 1.041 1.0764 0.8636 1.0238 1.0378 1.0468 0.9671 1.0173 1.0293 1.0248 1.0054 1.0099 1.0199 1.0081 0.98 0.9932 0.9873 0.9468 1.1956 0.9793 0.9725 0.9465 1.195 1.0141 1.0275 1.0653 1.054 1.0237 1.0377 1.0527 1.011 1.0188 1.0309 1.0293 1.0265 1.0119 1.0233 1.0125 1.0224 0.9969 0.9937 0.9516 0.9995 0.9846 0.9774 0.9346 0.9978 0.9991 1.0056 1.0298 1.0181 1.0216 1.035 1.0562 1.0176 1.0194 1.0314 1.0336 0.9851 1.0141 1.0255 1.0163 1.0382 1.011 1.0249 1.9331 1.1071 0.9912 0.985 0.9342 0.9902 0.9872 0.9866 0.981 1.0136 1.017 1.0287 1.0544 1.0167 1.019 1.0304 1.037 1.0103 1.0154 1.0265 1.0198 0.9875 1.0112 1.0225 1.0071 1.0325 0.9974 0.9926 0.9381 0.9935 0.9844 0.9798 0.9429 1.0074 1.0094 1.0183 1.0435 1.0147 1.0173 1.0277 1.0388 1.0143 1.0157 1.0261 1.0225 0.9384 1.0126 1.0236 1.0096

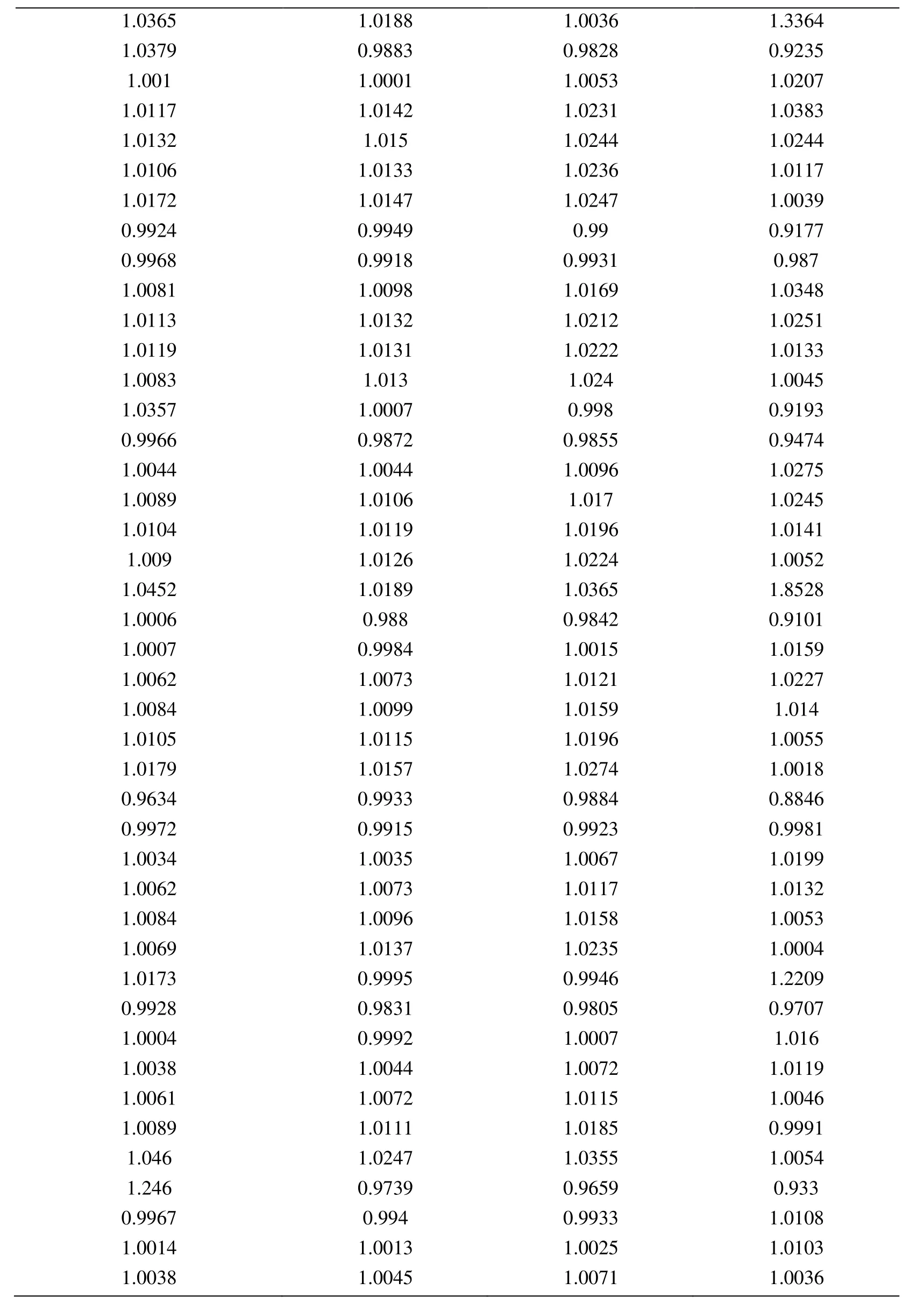
1.0365 1.0188 1.0036 1.3364 1.0379 0.9883 0.9828 0.9235 1.001 1.0001 1.0053 1.0207 1.0117 1.0142 1.0231 1.0383 1.0132 1.015 1.0244 1.0244 1.0106 1.0133 1.0236 1.0117 1.0172 1.0147 1.0247 1.0039 0.9924 0.9949 0.99 0.9177 0.9968 0.9918 0.9931 0.987 1.0081 1.0098 1.0169 1.0348 1.0113 1.0132 1.0212 1.0251 1.0119 1.0131 1.0222 1.0133 1.0083 1.013 1.024 1.0045 1.0357 1.0007 0.998 0.9193 0.9966 0.9872 0.9855 0.9474 1.0044 1.0044 1.0096 1.0275 1.0089 1.0106 1.017 1.0245 1.0104 1.0119 1.0196 1.0141 1.009 1.0126 1.0224 1.0052 1.0452 1.0189 1.0365 1.8528 1.0006 0.988 0.9842 0.9101 1.0007 0.9984 1.0015 1.0159 1.0062 1.0073 1.0121 1.0227 1.0084 1.0099 1.0159 1.014 1.0105 1.0115 1.0196 1.0055 1.0179 1.0157 1.0274 1.0018 0.9634 0.9933 0.9884 0.8846 0.9972 0.9915 0.9923 0.9981 1.0034 1.0035 1.0067 1.0199 1.0062 1.0073 1.0117 1.0132 1.0084 1.0096 1.0158 1.0053 1.0069 1.0137 1.0235 1.0004 1.0173 0.9995 0.9946 1.2209 0.9928 0.9831 0.9805 0.9707 1.0004 0.9992 1.0007 1.016 1.0038 1.0044 1.0072 1.0119 1.0061 1.0072 1.0115 1.0046 1.0089 1.0111 1.0185 0.9991 1.046 1.0247 1.0355 1.0054 1.246 0.9739 0.9659 0.933 0.9967 0.994 0.9933 1.0108 1.0014 1.0013 1.0025 1.0103 1.0038 1.0045 1.0071 1.0036

1.007 1.0081 1.013 0.9978 1.0066 1.0175 1.0278 1.0009 0.8662 0.9757 0.9506 0.8968 0.9914 0.9872 0.9835 1.0036 0.9988 0.9978 0.9974 1.0084 1.0015 1.0017 1.0027 1.0024 1.0041 1.005 1.0077 0.9963 1.006 1.0123 1.0189 0.9965 1.1015 1.0335 1.0601 1.519 0.9832 0.9785 0.9701 0.9938 0.9957 0.9939 0.9914 1.0063 0.9993 0.9988 0.9983 1.0011 1.0016 1.002 1.0028 0.9949 1.0061 1.0074 1.0108 0.9927 1.0209 1.0247 1.0367 1.027 0.9263 0.9698 0.9556 0.9832 0.9916 0.9894 0.9843 1.0038 0.997 0.9958 0.9937 0.9998 0.9993 0.999 0.9983 0.9935 1.0023 1.0032 1.0041 0.9896 1.0009 1.0153 1.0212 1.0113 0.8531 0.9045 0.9126 0.9749 0.9864 0.9844 0.9761 1.0008 0.9943 0.9927 0.9887 0.9987 0.9972 0.9962 0.994 0.9922 0.9995 0.9996 0.9986 0.9871 1.0035 1.0078 1.0093 0.9983 1.0395 1.0193 1.0323 1.1364 1.1166 0.9796 0.9679 0.9973 0.9913 0.9896 0.9834 0.9976 0.9949 0.9935 0.9896 0.9911 0.9971 0.9964 0.9938 0.9848 1.0005 1.0021 1.0009 0.9887 0.9887 1.0149 1.0198 1.09 0.9124 0.9807 0.9616 0.9938 0.9882 0.9869 0.9783 0.9968 0.9926 0.9909 0.9853 0.9904 0.9948 0.9934 0.9893 0.983 0.9975 0.9976 0.9945 0.9818 0.9983 1.0085 1.0088 1.0444 0.9887 0.9841 0.9762 1.9021 0.9851 0.9845 0.9738 0.996 0.9903 0.9886 0.9813 0.9901

0.9925 0.9906 0.9851 0.9818 0.9948 0.9937 0.9891 0.9767 0.9994 1.0031 1.0005 1.0113 0.9816 1.0021 1.0063 1.1306 0.9708 0.9829 0.9707 0.9954 0.9883 0.987 0.978 0.9905 0.9903 0.9883 0.9812 0.9813 0.9922 0.9902 0.9841 0.9732 0.9964 0.9973 0.9926 0.9881 0.9991 1.0073 1.0103 1.1085 0.9356 0.9587 0.9532 1.2238 0.9869 0.9862 0.9757 0.9914 0.9885 0.9866 0.978 0.9818 0.9897 0.9872 0.9797 0.9712 0.9932 0.9918 0.9853 0.9726 1.002 1.008 1.0088 1.0719 0.9786 0.9938 1.0016 1.0918 1.0516 0.9861 0.9747 0.9927 0.9873 0.9858 0.976 0.9832 0.9875 0.985 0.9761 0.971 0.9897 0.987 0.9786 0.9633 0.9998 1.0031 1.0006 1.0279 0.9995 1.0042 1.0095 1.0967 0.9346 0.9886 0.9745 0.9937 0.9996 0.986 0.9752 0.9854 0.9881 0.9837 0.9736 0.9722 0.9893 0.9833 0.9733 0.9589 0.998 0.9946 0.9881 0.9872 1.0047 1.0104 1.016 1.0946 0.9821 0.9928 0.9881 2.0273 1.0395 0.9869 0.9757 0.9881 0.9926 0.9834 0.9725 0.9747 0.9934 0.9809 0.9697 0.9585 0.9993 0.9859 0.9757 0.959 1.0019 1.013 1.0174 1.0777 0.9752 1.0028 1.0082 1.0725 0.9968 0.9884 0.977 0.9909 1.0068 0.9841 0.9728 0.9781 0.9976 0.9799 0.9679 0.9609 1.002 0.9795 0.9669 0.9457 1.0033 1.0077 1.0074 1.0368 0.9844 1.009 1.0158 1.0795 0.9635 0.9772 0.9686 1.2973

1.0207 0.9857 0.9742 0.9819 0.9979 0.98 0.9678 0.9648 1.0004 0.9762 0.9623 0.9434 1.0056 0.9939 0.9859 0.9801 0.9915 1.0153 1.0232 1.0832 0.9699 1.0001 1.0073 1.0563 0.9809 0.988 0.9766 0.9861 0.9857 0.9811 0.9688 0.9694 0.9814 0.9753 0.961 0.9471 0.9818 0.9799 0.9654 0.9391 1.0025 1.0194 1.0265 1.0748 1.0027 1.0074 1.0139 1.0633 0.9565 0.9924 0.98 0.9906 0.9669 0.9828 0.9708 0.9743 0.9516 0.9759 0.9619 0.9531 0.9375 0.9725 0.9553 0.9265 1.0115 1.0141 1.0152 1.0352 1.0479 1.0135 1.0215 1.0706 0.9747 0.9994 0.9976 2.0044 0.9234 0.987 0.9735 0.9791 0.9328 0.9811 0.9639 0.9596 0.9089 0.9774 0.9534 0.9304 0.9686 0.9992 0.9835 0.964 1.0739 1.0146 1.0298 1.0757 1.0664 1.0017 1.012 1.0516 0.8823 0.9599 0.9469 1.0836 0.9341 0.9425 0.9339 0.9938 0.9017 0.9181 0.9198 0.8794 0.9038 0.9023 0.9242 0.8112 1.1002 1.0569 1.0351 1.2088 1.1096 1.0431 1.0125 1.1238