Some Remarks on the Method of Fundamental Solutions for Two-Dimensional Elasticity

M.R.Hematiyan,M.ArezouN.Koochak Dezfouli and M.Khoshroo

1Department of Mechanical Engineering,Shiraz University,Shiraz,71936,Iran.

Abstract:In this paper,some remarks for more efficient analysis of two-dimensional elastostatic problems using the method of fundamental solutions are made.First,the effects of the distance between pseudo and main boundaries on the solution are investigated and by a numerical study a lower bound for the distance of each source point to the main boundary is suggested.In some cases,the resulting system of equations becomes ill-conditioned for which,the truncated singular value decomposition with a criterion based on the accuracy of the imposition of boundary conditions is used.Moreover,a procedure for normalizing the shear modulus is presented that significantly reduces the condition number of the system of equations.By solving two example problems with stress concentration,the effectiveness of the proposed methods is demonstrated.

Keywords:Method of fundamental solutions,elastostatic,location parameter,configuration of source points,Ill-conditioned system of equations,shear modulus normalizing.

1 Introduction

Nowadays,the method of fundamental solutions (MFS) is widely used by engineers and scientists in a variety of applications.The MFS has a great capability to provide very accurate solutions [Alves (2009);Tsai and Young (2013)] without considering any unknown variable within the domain of the problem.A few different boundary-type meshfree techniques have also been proposed and developed which are different but related to the MFS,see for example [Zhang,Gu,Hua et al.(2018);Liu,Wang and Qu (2018);Gu,Fan and Xu (2019)].Many important meshfree methods based on weak form formulation have been proposed,in which efficient evaluation of domain integrals requires special techniques [Chen,Yoon and Wu (2002);Hematiyan,Khosravifard and Liu (2014);Jamshidi,Hematiyan and Mahzoon (2019)];however,the MFS is an integration-free strong-form meshfree method.

Besides these advantages,the MFS involves some difficulties,which have restricted its fast development,especially in engineering fields.The proper determination of the location of source points and solving the resulting ill-conditioned system of equations are important issues,which should be dealt with in the MFS.

Until now,several researches have been conducted for proper determination of the location of source points in the MFS.Tsai et al.[Tsai,Lin,Young et al.(2006)] investigated on the MFS for Laplace,Helmholtz,modified Helmholtz,and biharmonic equations and found out that more accurate solutions can be obtained by considering source points farther from the boundary.They also mentioned that the condition number of the system of equations increases by increasing the distance between main and pseudo boundaries and concluded that this distance should be limited with an attention to the capability of the system solver.Gorzelańczyk et al.[Gorzelańczyk and Kołodziej (2008)] investigated on the analysis of the torsion problem with the Poisson’s governing equation using the MFS,where they employed the fundamental solution of the two-dimensional Laplace equation.They examined circular pseudo boundaries and source contours geometrically similar to the main boundary and concluded that the latter leads to much more accurate results.

Karageorghis [Karageorghis (2009)] proposed an optimization method with one variable for determining the suitable distance between pseudo and main boundaries in the MFS.He examined harmonic and biharmonic boundary value problems with different boundary conditions.Wong et al.[Wong and Ling (2011)] proposed an optimization method for determining the suitable configuration of the pseudo boundary in the MFS for Laplace equation.They considered two cases with one optimization variable.In the first case,the distance between main and pseudo boundaries was the unknown of the optimization problem,while in the second case,this distance was fixed and the number of source points was the unknown of the optimization problem.Liu [Liu (2012)] introduced an optimization method for location of source points in the MFS for the Laplace equation.He considered one unknown distance factor for each source point and could find the unknowns by solving an uncoupled system of nonlinear equations.Li et al.[Li,Chen and Karageorghis (2013)] investigated on different configurations of collocation and source points in the MFS for 2D Laplace equation.They observed that placing the source points on a circle leads to poor results and recommended pseudo boundaries similar to the main boundary of the problem.

Chen et al.[Chen,Karageorghis and Li (2016)] investigated on the configuration of source points in the MFS for 2D and 3D boundary value problems governed by the Laplace and biharmonic equations.They used an optimization algorithm based on the accuracy of the imposition of boundary conditions for proper determination of the location of source points.Hematiyan et al.[Hematiyan,Haghighi and Khosravifard (2018)] proposed a method for determining the location of collocation and source points in the MFS for the 2D Laplace equation without any optimization process.They introduced a new index,namely “the location parameter” for source points that expresses the location of the source point relative to its neighboring source and collocation points.They showed that values greater than 0.8 are suitable for the location parameter of source points in the MFS for the 2D Laplace equation.This method was successfully used by Mohammadi et al.[Mohammadi,Hematiyan and Khosravifard (2019)] for selecting the position of source points in the MFS for steady-state heat conduction analysis.

Grabski et al.[Grabski and Karageorghis (2019)] applied the MFS for potential boundary value problems,in which both intensity and position of source points were unknown.This approach yields a system of nonlinear equations.Recently,Grabski [Grabski (2019)] examined four different configurations of source points for analysis of transient heat conduction problems using the MFS.He observed that the results were more accurate in the cases that source points were located further from the main boundary of the problem.

As it is seen,most of the above-mentioned researches on the location of source points in the MFS are devoted to boundary value problems with the Laplace,Helmholtz,and biharmonic equations.The investigations on the configuration of source points in the MFS for elastostatic problems have been very rare;however,the MFS formulation for 2D and 3D elastostatic problems have been considered by several researches that are briefly reviewed here.

Berger et al.[Berger and Karageorghis (2001)] used the MFS for analysis of elastostatic problems in 2D isotropic and anisotropic domains.They analyzed domains with one or two materials.Poullikkas et al.[Poullikkas,Karageorghis and Georgiou (2002)] applied the MFS to 3D isotropic elastostatic problems.Similar to the work by Berger et al.[Berger and Karageorghis (2001)],components of pseudo forces and their locations were considered as unknowns of the problem in this work.De Medeiros et al.[De Medeiros,Partridge and Brandão (2004)] formulated the MFS with the dual reciprocity method for analysis of 2D elastostatic problems involving body forces.They considered circular pseudo boundaries and used singular value decomposition for solving the MFS system of equations.Marin et al.[Marin and Lesnic (2004)] and Marin [Marin (2005)] used the MFS for the Cauchy problem in 2D and 3D elasticity,respectively.They observed that the error of solutions decreases by increasing the distance between pseudo and main boundaries.Fam et al.[Fam and Rashed (2005)] used the MFS with a new set of particular solutions to solve 3D elastostatic problems involving body forces.They derived particular solutions in explicit forms for displacements and stresses using a decoupling technique.They located the source points on a pseudo boundary similar to the main boundary of the problem.

Tsai [Tsai (2009)] developed the MFS with the dual reciprocity for analysis of 3D thermoelastic problems involving body forces.He observed that using truncated singular value decomposition (TSVD) could improve the accuracy of the obtained results.Marin et al.[Marin and Karageorghis (2013)] formulated the MFS with the method of particular solutions for analysis of thermoelastic problems.They derived new particular solutions for the nonhomogeneous equilibrium equations.Marin et al.[Marin and Karageorghis (2013a,2013b);Marin,Karageorghis and Lesnic (2015)] used the MFS for inverse analysis of inverse thermoelastic problems too.Sun et al.[Sun and Marin (2017)] proposed an invariant method of fundamental solutions for analysis of 2D elastostatic problems.They used the Tikhonov regularization method and the discrepancy principle and obtained very accurate solutions.Askour et al.[Askour,Tri,Braikat et al.(2018)],by combination of the MFS,the asymptotic numerical method,and the analog equation method,developed a technique for analysis of nonlinear elastic problems.They also used the TSVD and Tikhonov regularization methods for solving the resulting ill-conditioned system of equations.

As it can be seen from the above review,several researches have been conducted on the configuration of source points in the MFS analysis of boundary value problems with the Laplace,Helmholtz,and biharmonic equations;however,to the authors’ best knowledge,no research devoted to the configuration of source points for the MFS analysis of elastostatic problems has been reported yet.In the present work,a procedure for determining a suitable configuration of source points in the MFS for 2D elastostatic problems is presented.A criterion based on the accuracy of imposition of boundary conditions is employed for solving the resulting ill-conditioned system of equations using the TSVD.Moreover,a method for reducing the condition number of system of equations by normalizing the shear modulus is suggested.By analyzing two example problems with stress concentration,it is shown that the proposed methods can be efficiently used for analysis of complicated 2D elastostatic problems.

2 The MFS for 2D elastostatic problems

In the absence of body forces,the governing equations for elastostatic problems are expressed as follows:

where σ and ε are the stress and strain tensors,respectively;u is the displacement vector,νandGare the Poisson’s ratio and shear modulus,respectively,and x is a point within the problem domain Ω or over its boundary Γ.The shear modulusGcan be expressed in terms of the elastic modulusEasG=E/ 2(1+ν).The unknowns in a 2D elastostatic problem areu1,u2,ε11,ε12,ε22,σ11,σ12,andσ22.

Boundary conditions at a boundary point of a 2D elasto-static problem can be expressed as follows:

whereunandutare normal and tangential displacement,respectively,andtnandttare normal and tangential components of the traction vector at the boundary point.,,tn,andttare given functions.As it is seen from Eqs.(4) and (5),two boundary conditions are considered at a boundary point.Boundary conditions at a boundary point of a 2D problem in a generalized form can be expressed as follows:

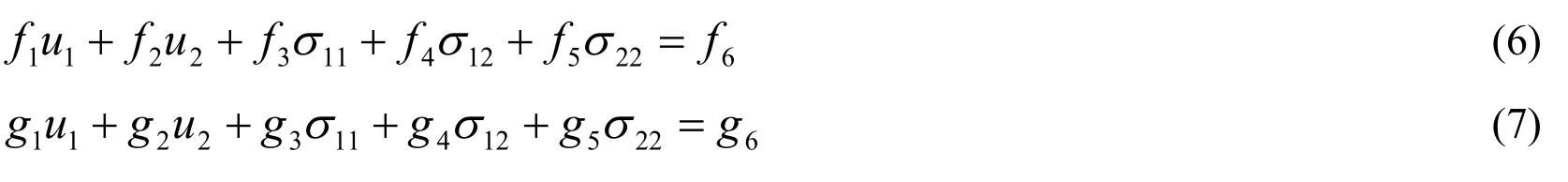
wherefαandgαwithα= 1,2,…,6 are given functions.For example,for a boundary point withu1=1 andσ12=0 as its boundary conditions,we havef1=1,f6=1,g4=1,while other functions offαandgαare zero.We describe the MFS formulation for plane strain problems only.A plane stress problem formulated in terms of the elastic constantsνandGcan be solved by a solver of plane strain problems by changingνintoν(1+ν),while the shear modulus is not changed.

In the MFS withNsources (fictitious concentrated force),the displacement solution of the 2D elastostatic problem is expressed as follows:

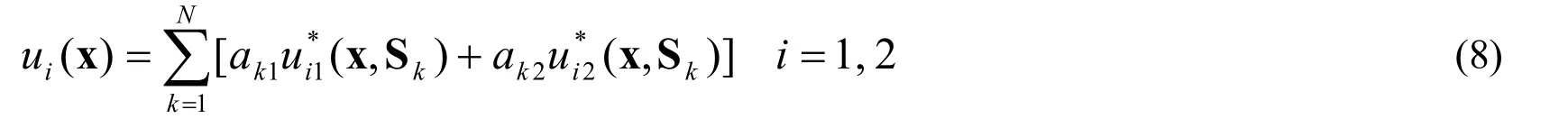
ak1andak2are the components of thekth concentrated force (source),which are to be determined.Skwith coordinates (ξk,ηk) represents the location of thekth source point and x with coordinates (x,y) represents a point of the domain.The displacement fundamental solutions for 2D plane strain problems are given by the following equations [Berger and Karageorghis (2001)]:

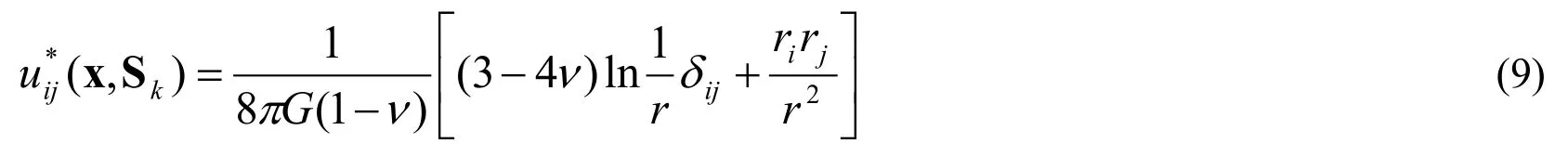
By substituting Eq.(8) into Eq.(2) the components of the strain tensor are found as follows:

where

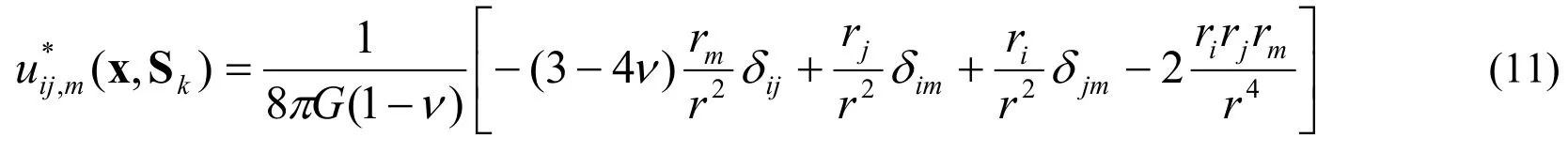
The stress components are found by substituting Eq.(10) into Eq.(3).For plane strain problems withε33=ε13=ε23=0 the following equations are obtained:

where

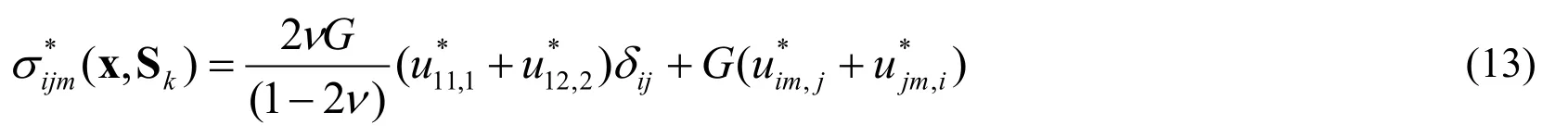
There are 2Nunknowns,i.e.,ak1andak2withk=1 toN.We considerM(M≥N) collocation points C1,C1,...,CMover the boundary Γ.By using Eqs.(8) and (12) and satisfying Eqs.(6) and (7) for theMcollocation points,the following system of 2Mequations are obtained:

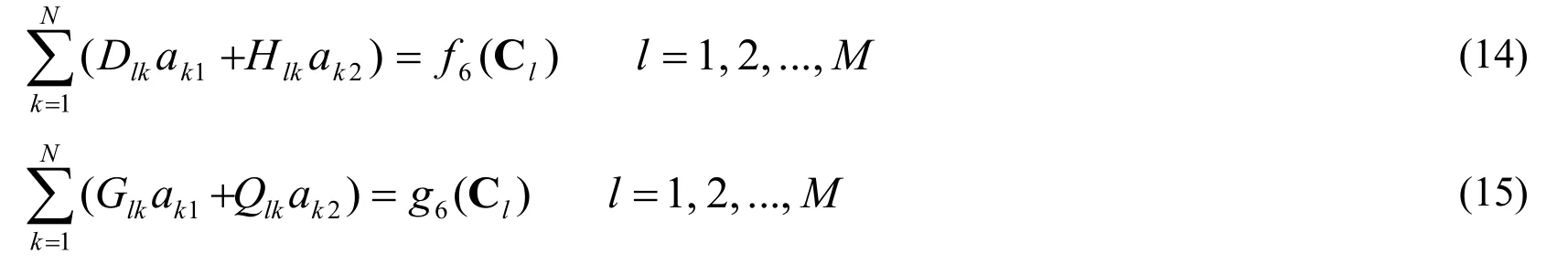
where

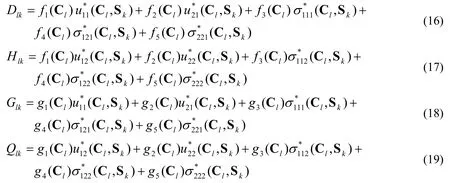
The system of equations given in Eqs.(14) and (15) can be expressed as follows:

where

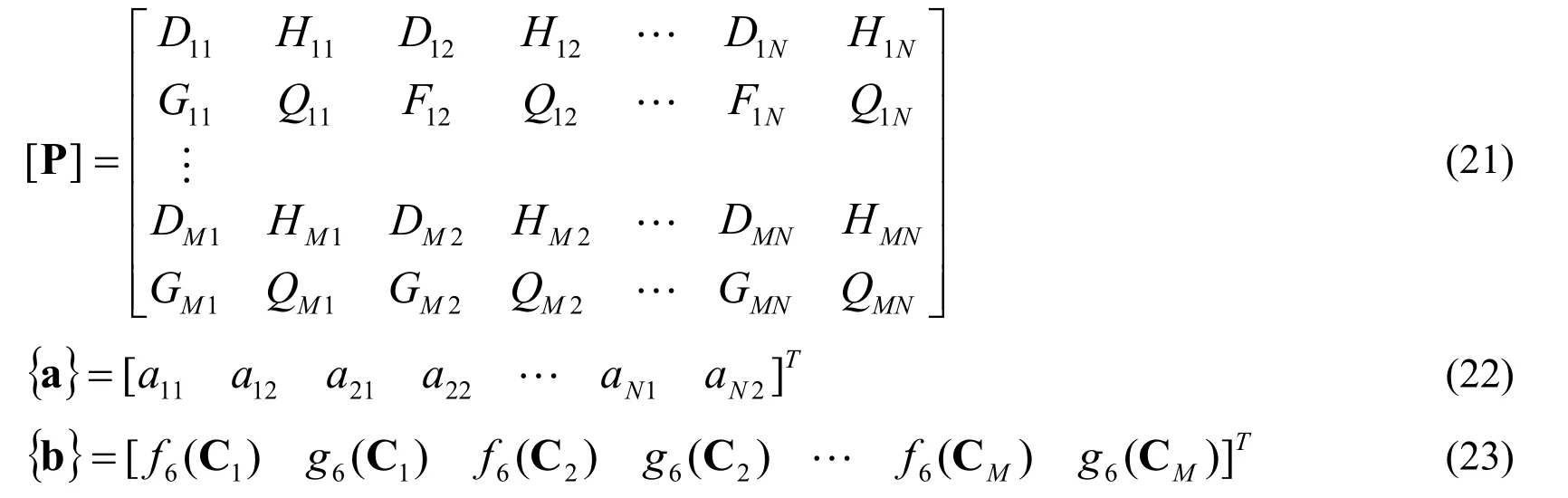
Eq.(20) represents a system of 2Mlinear equations with 2Nunknowns.For the cases withM=N,the system may be solved by a standard system solving method;however,the system should be solved using an ordinary least-squares method for the cases withM＞N.

For elastostatic problems with a body force or elastodynamic problems,a nonhomogeneous term appears in Eq.(1).In the MFS and other methods that use point collocation,the nonhomogeneous term can be treated using particular solutions [Liu,Wang and Qu (2018)].

3 A suitable configuration for source points in the MFS for 2D elasticity

The configuration of source points in the MFS has a noticeable effect on the accuracy of the solution.If source points are located very close to the boundary,the solution would experience undesired oscillations on the boundary.On the other hand,if source points are located very far from the boundary,we confront an ill-conditioned system of equations.Hematiyan et al.[Hematiyan,Haghighi and Khosravifard (2015,2018)] have introduced a parameter for each source point that describes the position of the source point relative to the physical boundary and relative to its neighbouring source points.This parameter has been called the location parameter,which is defined as follows:

whereKirepresents the location parameter for the source point Si.Other parameters in Eq.(24) can be defined according to Fig.1.The source point Siis shown in Fig.1.Spand Snare the previous and next source points,respectively.We also consider a base point on the physical boundary for each source point.The base point of the source point Siis denoted by Bi,which is a point on the boundary with the smallest distance to the source point Si.As shown in Fig.1,the base points of the source points Spand Snare represented by Bpand Bn,respectively.dii,dip,anddinin Eq.(24) are the distances from the source point Sito the base points Bi,Bp,and Bn,respectively.A large value of the location parameter of source points means that the distance between pseudo and physical boundaries is large in comparison with the distance between two adjacent source points.For a problem with a large value of the location parameter of source points,the local effect of each source (pseudo force) on the boundary reduces and therefore,the condition number of the coefficient matrix becomes large.For simple geometries such as a circular domain,with regular boundary conditions,larger values of the location parameter lead to more accurate solutions if a sufficiently accurate system solver is used [Hematiyan,Haghighi and Khosravifard (2018)].

Figure 1:Location of a source point relative to the physical boundary and relative to its neighboring source points

It has been observed that a location parameter greater than 0.80 is suitable for source points in the MFS for problems with the Laplace fundamental solutions [Hematiyan,Haghighi and Khosravifard (2018)].In this section,by a numerical study it is observed that a location parameter greater than 0.85 is suitable for source points in the 2D elastostatic problems.

Suppose that we want to solve an elastostatic problem in a circular domain as shown in Fig.2.The radius of the circle is 1.0 and boundary conditions areur=0.5 anduθ=0.

The elastic constants areE=1.0 andν= 0.3.This problem is solved using the MFS with 16 source points and 16 collocation points.

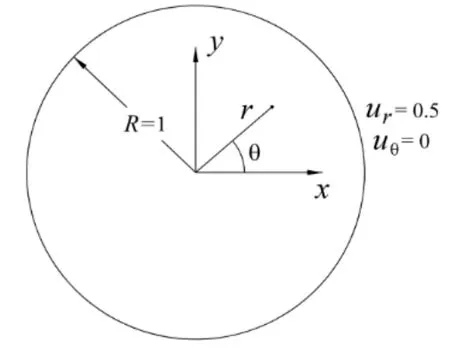
Figure 2:A circular domain with simple boundary conditions

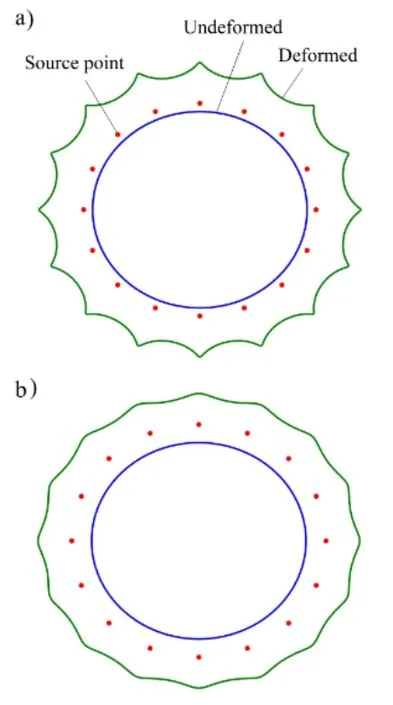
Figure 3:The solution of the circular problem with a) K =0.2,b) K =0.4

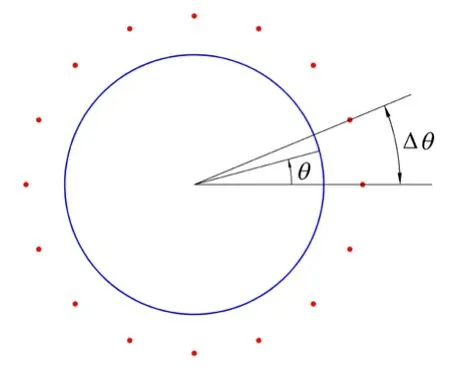
Figure 4:The angle covered by two adjacent source points

The obtained solutions for the deformed shape in two different cases with location parameters of 0.2 and 0.4 for source points are shown in Fig.3.The exact solution foruris uniform over the boundary;however,as it can be seen in Fig.3,the solution obtained by the MFS has a local oscillation.Also it is observed that the oscillation in the case withK=0.2 (Ki= 0.2,i= 1,2,...,N) is more than that withK=0.4.

Figure 5:Variation of ur between two adjacent base point a) N=16,b) N=64,c) N=256

For further study,we consider different cases with different numbers of source points (N=16,64,256,1024) and different values of the location parameter.The angle covered by two adjacent source points is denoted by Δθas shown in Fig.4.By increasing the number of source points,the value of Δθdecreases.For the case withN=16,the value of Δθisπ/ 8 (Fig.4),where the boundary between two adjacent base points has a curved shape.For the case withN=1024,the value of Δθisπ/ 512,which is small angle and it means the boundary between two adjacent base points in this case is approximately a straight line.The solution of the MFS for radial displacement (ur) and radial stress (σ r) between two adjacent base points for different values of the location parameter and different number of source points are shown in Figs.5 and 6,respectively.The exact solutions forurandσrare uniform over the boundary;however,the solution of the MFS has some oscillations over the boundary.From Figs.5 and 6,it is observed that the solutions have an undesired oscillation in the cases withK＜0.85.For better clarification,the values ofandfor different values ofNandKat the midpoint between two adjacent base pointsare given in Tab.1.It should be mentioned that the maximum values ofurandσroccur at base (collocation) points,i.e.,atand

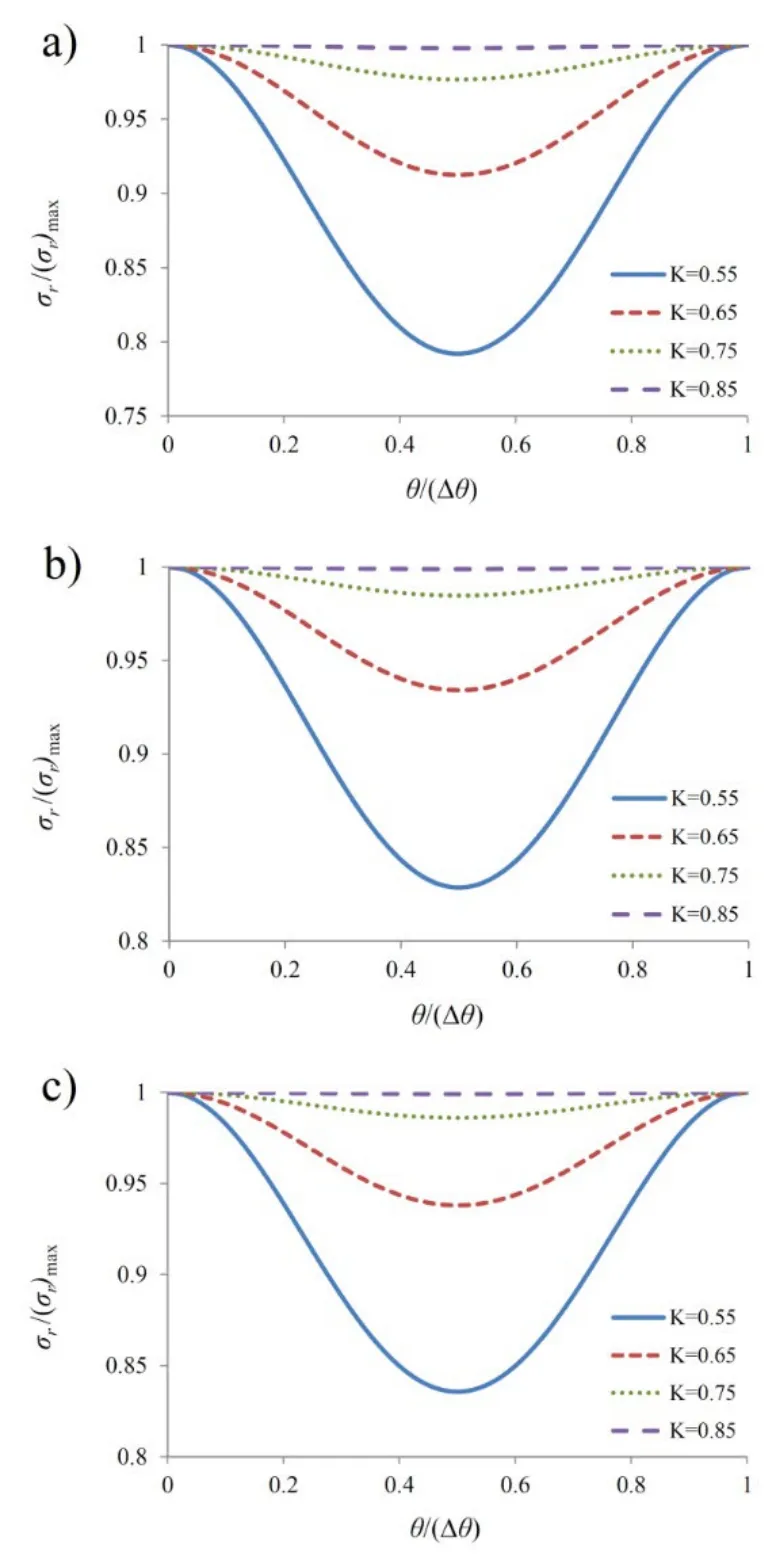
Figure 6:Variation of rσ between two adjacent base point a) N=16,b) N=64,c) N=256

Table 1:Values of and for different values of N and K at the midpoint between two adjacent base points ( =0.5)

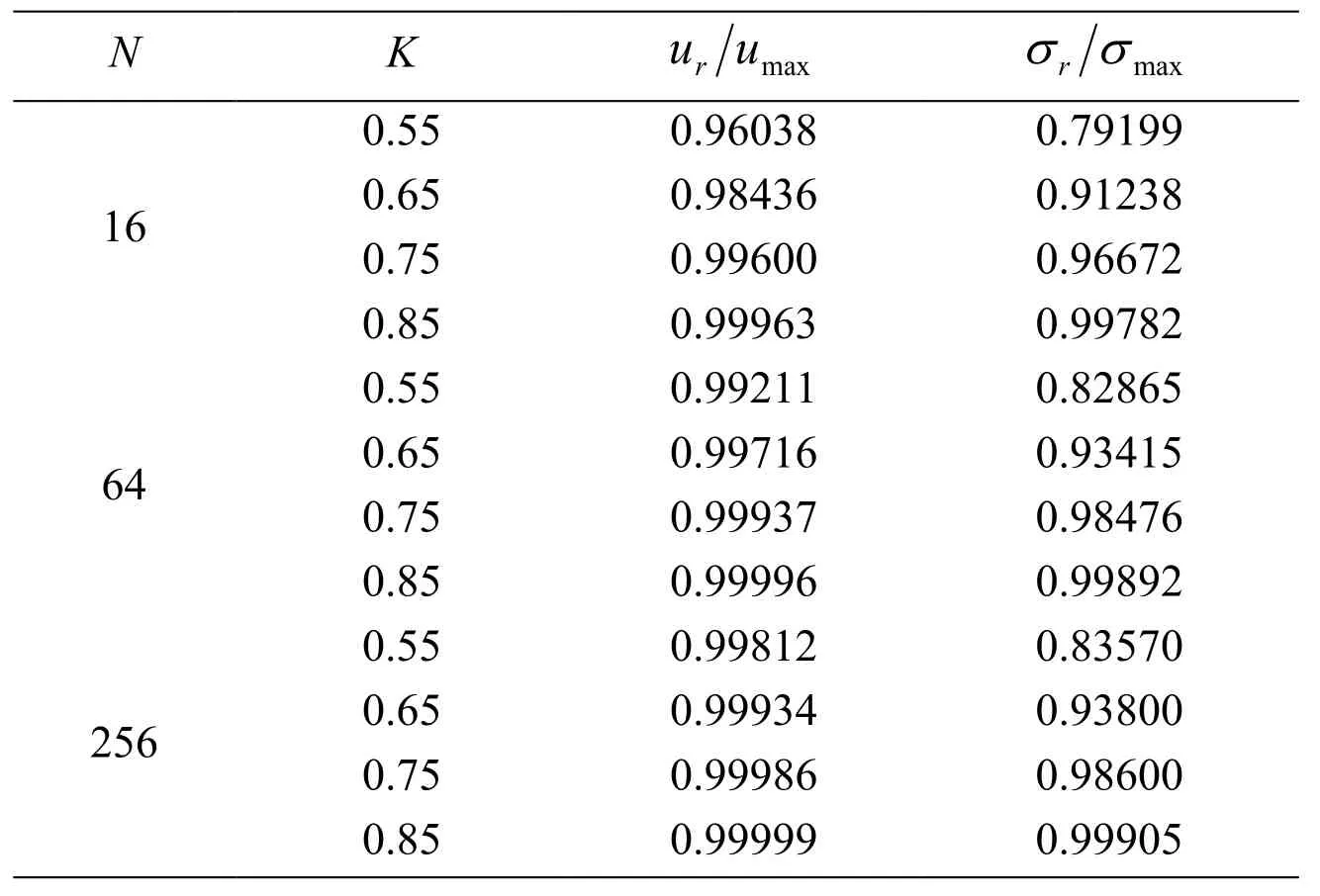
Table 1:Values of and for different values of N and K at the midpoint between two adjacent base points ( =0.5)

N K urumax σrσmax 0.55 0.96038 0.79199 16 0 0..67 55 00..99 89 46 30 60 00..99 16 26 37 82 0.85 0.99963 0.99782 0.55 0.99211 0.82865 64 0 0..67 55 00..99 99 79 13 67 00..99 38 44 17 56 0.85 0.99996 0.99892 0.55 0.99812 0.83570 256 0 0..67 55 00..99 99 99 38 46 00..99 38 86 00 00 0.85 0.99999 0.99905

We also define the following oscillation factors:

wherefdisp.andfstressare the displacement and stress oscillation factors,respectively.(u r)maxand (u r)minare respectively,maximum and minimum values of radial displacement over the boundary between two adjacent base points.Similarly,(σ r)maxand (σ r)minare maximum and minimum radial stresses.Smaller oscillation factor corresponds to less oscillation.Fig.7 shows the variation offdisp.with respect to the value of the location parameter of source points (K).It is observed that forK≥0.85 we havefdisp.＜3.7×10-4.The variation offstresswith respect toKfor different numbers of source points is shown in Fig.8.It can be seen that forK≥0.85 we havefstress＜2.2×10-3.Figs.7 and 8 show that the oscillation of stress is more than that of displacement.However,the oscillations are very small forK≥0.85.It should be noted that larger values ofKcorrespond to larger distances between main and pseudo boundaries and also larger values of the condition number.

Here,we analyzed circular domains.More complicated geometries are studied in Section 6.It is worth mentioning that Hematiyan et al.[Hematiyan,Haghighi and Khosravifard (2018)] have recommendedK≥0.8 for 2D problems with the Laplace operator;however,the present study shows that the location parameter for source points should be more than 0.85 for 2D elastostatic problems.Moreover,it should be mentioned that a configuration of source points withK≥0.85is a suitable configuration for 2D elastostatic problems but not necessarily the optimum one.

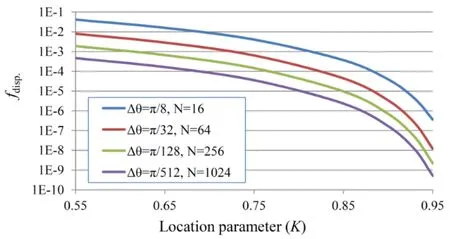
Figure 7:Displacement oscillation factor with respect to the location parameter

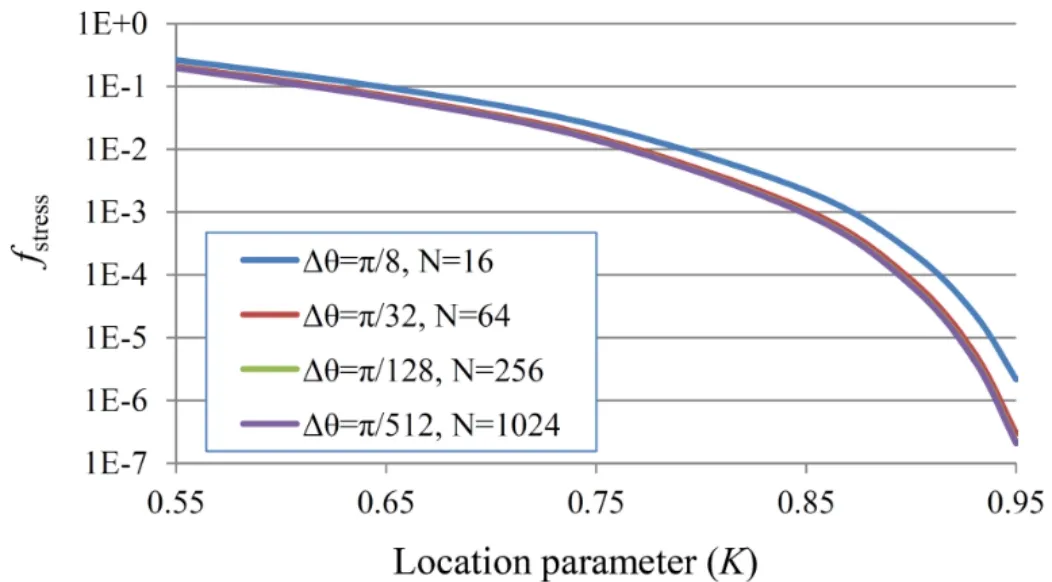
Figure 8:Stress oscillation factor with respect to the location parameter

4 System solving using the singular value decomposition and a suitable truncation criterion

As it was demonstrated in the previous section,for avoiding undesired local oscillation of the solution on the boundary,it is necessary to consider a sufficient distance between pseudo and physical boundaries.This leads to an ill-conditioned system of equations in some problems [Liu (2008)].Therefore,a reliable method should be used to solve the system of equations.The TSVD method has been widely used to solve ill-conditioned systems of equations (e.g.,[Ramachandran (2002);Chen,Cho and Golberg (2006);Feng Li and Chen (2014);Marin,Karageorghis and Lesnic (2016);Li,Lee,Huang et al.(2017)]).For efficient use of the TSVD method,a suitable criterion for neglecting some smallest singular values should be employed.In this work,a criterion based on the accuracy of the imposition of boundary conditions is used for truncation of a sufficient number of singular values.

For simplicity,we assume that the number of source points is equal to the number of collocation points,i.e.,M=N.Based on the SVD,the coefficient matrix [ P ](Z×Z)in Eq.(20) can be expressed as follows:

whereZ= 2Nand

[L] and [R ] in Eqs.(28) and (29) are orthonormal matrices,i.e.,[ L ] [L]T= [I]Z×Z,[ R ][R]T= [I]Z×Z,andλiin Eq.(30) are the singular values of the matrix [ P ](Z×Z)withλ1≥λ2≥…≥λZ.The condition number of [ P](Z×Z)can be computed as follows:

Based on the TSVD method,the solution of the system of Eq.(20) can be found as follows:

where the integer numberNTrepresents the number of truncated singular values.The suitable value forNTshould be selected based on a suitable criterion.Some criteria based on generalized cross validation [Golub,Heath and Wahba (1979)] and L-curve method [Hansen (1992);Hansen and O’Leary (1993)] have been proposed.In this work,an alternative criterion based on the accuracy of the MFS solution on the boundary is used for this purpose.In the MFS for elastostatic problems,the governing equations of the problem are exactly satisfied.Boundary conditions at collocation points are exactly satisfied too.However,the boundary conditions are approximately satisfied at other boundary points between collocation points.We consider a few test points between two neighbouring collocation points as shown in Fig.9.A value of the truncation parameter,i.e.,NT,which minimizes the summation of the errors of boundary conditions at test points (EΓ) is selected.We can start withNT=0 and then increaseNTand compute the correspondingEΓ.For an ill-conditions system of equations,the value ofEΓfirst decreases and then increases with increase ofNTand therefore the optimum value ofNTcan be simply found.

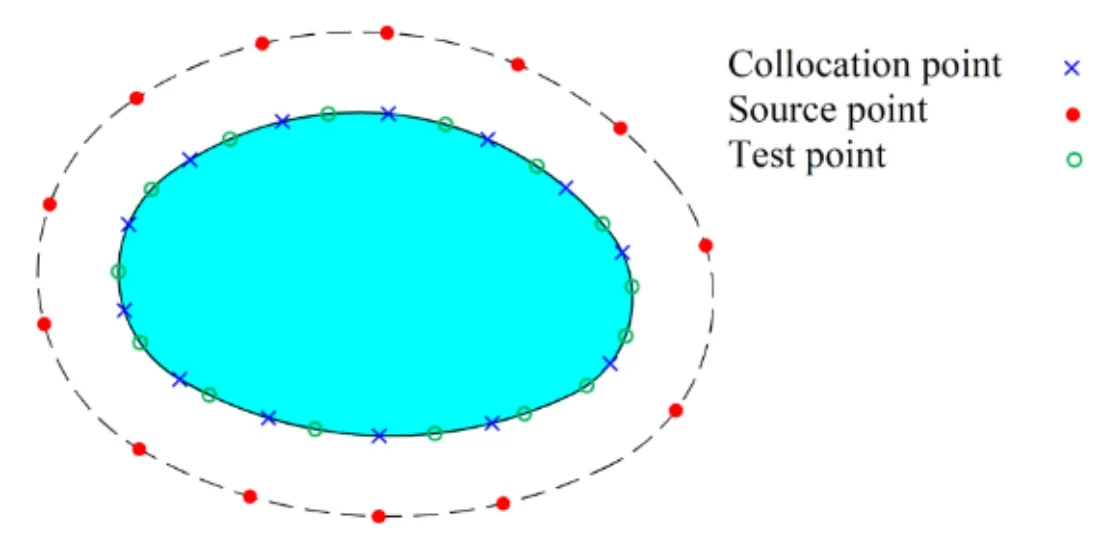
Figure 9:Collocation points,source points,and test points in the MFS modeling of a problem

5 Reducing the condition number of the system of equations by normalizing the shear modulus

In applied engineering problems with stiff materials such as metals,the magnitude of the shear modulus is very large.In these problems,the magnitude of the stress over a part of the boundary with natural boundary condition can be very large,e.g.,108Pa.On the other hand,in the same problems,the magnitude of the displacement is very small,e.g.,10-3m,on the boundaries with essential boundary conditions.Considering Eqs.(6) and (7),it is observed that equations corresponding to essential boundary conditions are expressed in terms of small numbers,while equations corresponding to natural boundary conditions are expressed in terms of very large numbers.It means that the numbers in some lines of the coefficient matrix are very small and in some other lines are very large.This configuration of numbers makes the coefficient matrix highly ill-conditioned.To avoid this issue,before solving the problem using the MFS,we set the shear modulus to the value of 1.0.Moreover,prescribed stresses in the natural boundary conditions are divided by the shear modulus.Then the problem is solved using the MFS.After that,the computed values for stresses should be multiplied by the shear modulus.For better explanation of this approach,we can rewrite the governing equations,i.e.,Eqs.(1),(2) and (3),as follows:

The traction vector on a boundary point with unit normal n,i.e.,σn= t,can be expressed aswhich shows that prescribed stresses on the boundary should be divided byGin the equivalent problem.

By this approach,the condition number of the coefficient matrix significantly reduces and the problem can be solved more accurately.The effectiveness of normalizing shear modulus is demonstrated in Section 6.

6 Examples

In this section,two examples with stress concentration are considered.In the first example,the stress concentration is due to the shape of the member,while in the second example the stress concentration is due to the presence of a concentrated load on the boundary.The locations of source points are determined based on the limitation proposed in this work.The system of equations in each example is solved by the TSVD using the criterion proposed in this study.

In an elastostatic problem,two boundary conditions are defined for each boundary point.The boundary data computed using the MFS at the test points have a difference with the prescribed one (exact values).There is usually a difference between the boundary data computed using the MFS with the exact ones (prescribed values) at test points.The error of boundary data at test points,i.e.,EΓ,is defined as follows:

whereuMFSanduEx.are the MFS and exact solutions for a displacement component andtMFSandtEx.represent the MFS and exact values of a traction component at a test point,respectively.uRef.andtRef.are reference values for displacement and traction,respectively.In this work,the maximum absolute values of displacement and traction are used foruRef.andtRef.,respectively.The total number of displacement and traction boundary data at test points are denoted byNuandNt,respectively.Therefore,Nu+Ntis twice the total number of test points.In this work,only one test point is considered between two adjacent collocation points.Each test point is located at the midpoint of two adjacent collocation points.

6.1 A plate with a circular hole

Consider an infinite plate with a circular hole of radiusaunder the uniform far-field tensionT.Assuming the center of the hole is placed at the origin of the coordinates system andTis applied in thex-direction,the solution for stress field can be expressed as follows [Sadd (2009)]:

where

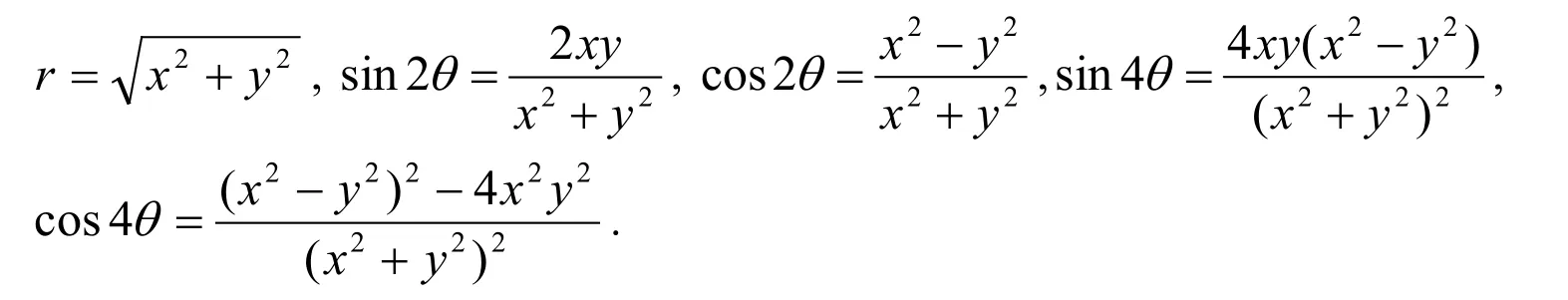
The maximum stress concentration occurs at (x,y)= (0,a),i.e.,pointAin Fig.10,whereσx=3T.

As shown in Fig.10,a finite part of the infinite plate,which includes a quarter of the hole,is considered in this example.Symmetric boundary conditions are considered for the left and lower edges of the domain as shown in Fig.10.For the right edge,i.e.,CD,Eqs.(37) and (39) are considered as boundary conditions,while for the upper edge,i.e.,BC,Eqs.(38) and (39) are used as boundary conditions.The problem is solved under plane stress condition withT=100 MPa,a=1 m,G=80 GPa,andν=0.3.

To solve the problem by the MFS,two cases with 58 and 118 collocation points are considered.The configurations of source and collocation points for these two cases are shown in Figs.11 and 12,respectively.In the first case withN=58,the distance between each source point to the main boundary of the problem is 0.75.In this case,the minimum and average values of the location parameter for source points are 0.85 and 0.95,respectively.In the second case withN=118,the distance between each source point to the main boundary of the problem is 0.65.In this case,the minimum and average values of the location parameter for source points are 0.93 and 0.98,respectively.In the two cases the minimum value of the location parameter is greater than 0.85.

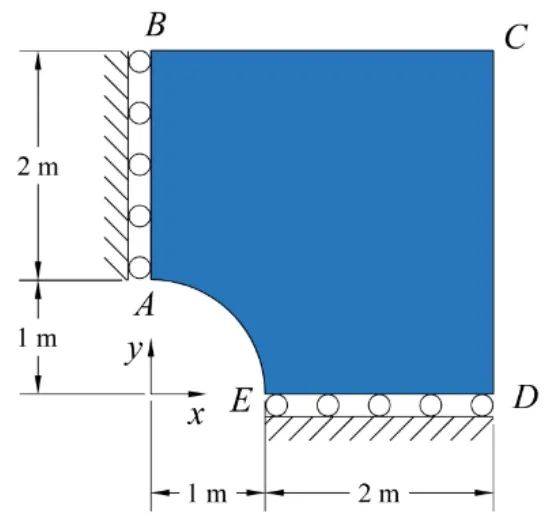
Figure 10:A plate with a hole

Figure 11:Configuration of 58 source and 58 collocation points for the plate with a circular hole

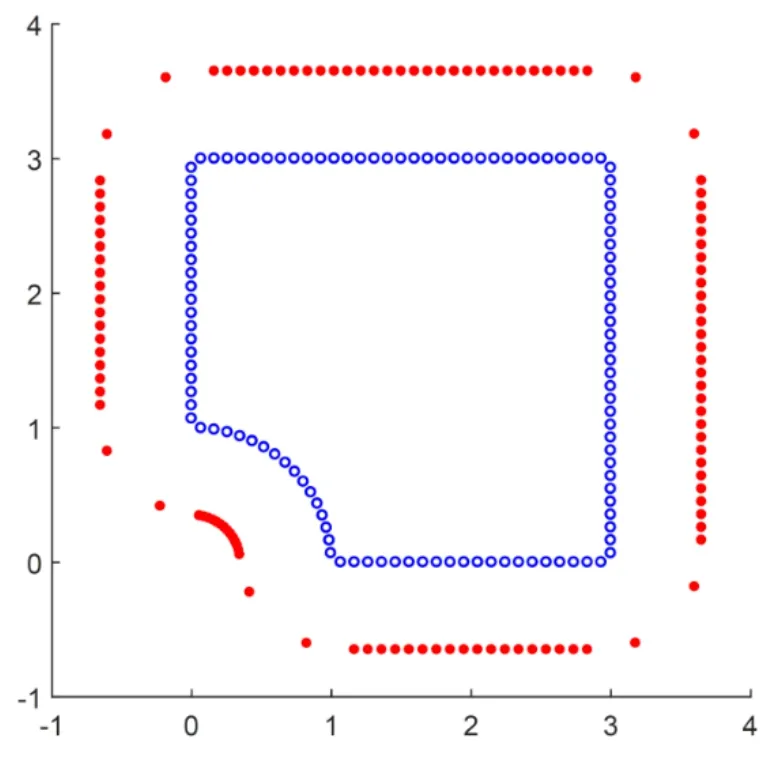
Figure 12:Configuration of 118 source and 118 collocation points for the plate with a circular hole

In the MFS analysis of the problem,the method described in Section 4 was used to solve the system of equations and it was observed that there was no need for truncating any singular value,i.e.,NT=0.The results for the normal stress along the edgeAB,obtained by the MFS in comparison with the exact solution are shown in Fig.13.As it can be observed,the results obtained by the MFS are in very good agreement with the exact solution.For better comparison of the results obtained withN=58 andN=118,the results for the normal stress in thex-direction at pointsAandBare reported in Tab.2.From Tab.2,it can be seen that the results obtained withN=58 is sufficiently accurate;however,the results corresponding toN=118 is more accurate.

The effects of the shear modulus normalizing (described in Section 5) on the results are also investigated in this example.The results for normal stresses at pointsAandBwith and without shear modulus normalizing are given in Tab.3.From this table,it is observed that the condition number significantly reduces by performing the shear modulus normalizing procedure.In the case without shear modulus normalizing,3 singular values are truncated;however,the error of the obtained results is more than the case with shear modulus normalizing.

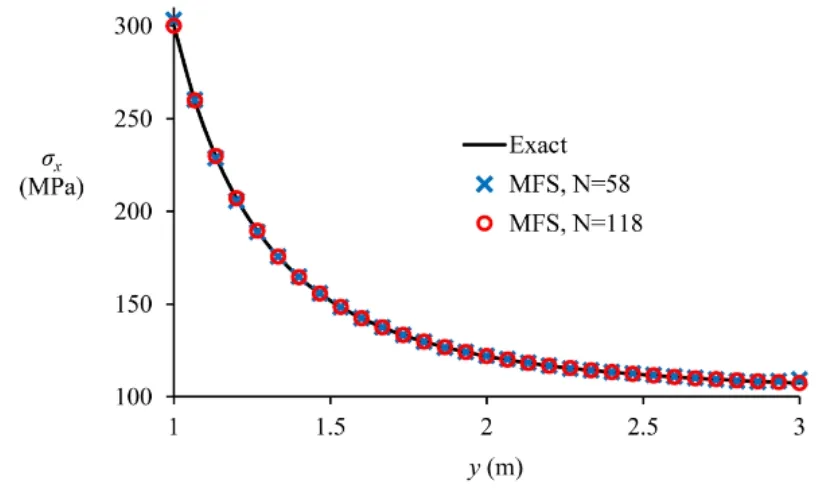
Figure 13:Results for the normal stress along the edge AB

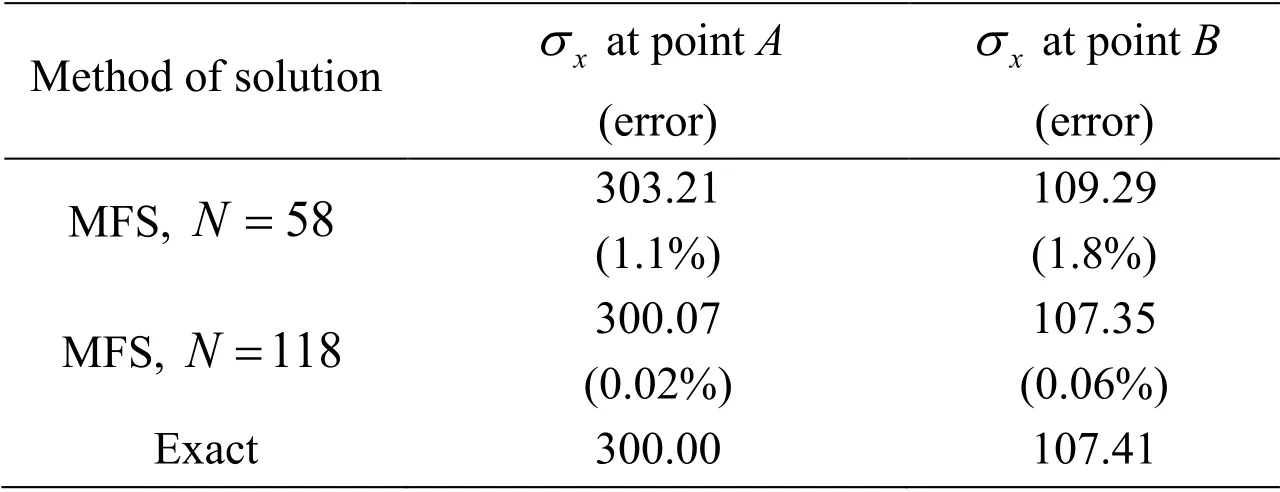
Table 2:The normal stress at points A and B in the plate with a hole

Table 3:The normal stress at points A and B in the plate with a hole,with and without shear modulus normalizing

6.2 A rectangular domain under a pressure with a sharp variation

In the previous example,the complexity in the geometry resulted in a stress concentration at a part of the domain.In the present example,a simple domain is considered;however,a load with a sharp variation causes a stress concentration at a part of the domain.

The geometry and boundary conditions of the problem are shown in Fig.14.The pressurep(x)=(1.52-x2)/(0.01+x2),which has a very sharp variation atx=0,is applied over the upper edge.The other edges of the rectangle are fixed in the normal direction and free in the tangential direction.The problem is solved under plane strain condition withE=200 GPa (G=76.92 GPa) andν=0.3.

To solve the problem by the MFS,two cases with 56 and 111 collocation points are considered.The configurations of source and collocation points for these two cases are shown in Figs.15 and 16,respectively.In both cases,near the critical point (0,0.5),a smaller distance between collocation points has been considered.In both cases,the location parameter for all source points around the critical point is 0.95.Therefore,the source points are located closer to the boundary around the critical point.

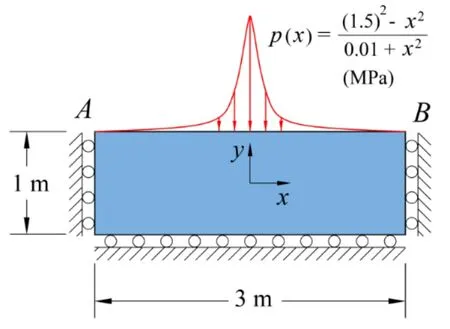
Figure 14:A rectangular domain under a pressure with a sharp variation

Figure 15:Configuration of 56 source and 56 collocation points for the rectangle

Figure 16:Configuration of 111 source and 111 collocation points for the rectangle

For comparison purposes,the problem has been solved by the finite element method (FEM) using ANSYS software too.To obtain an accurate solution at the critical point using the FEM,it is necessary to consider a very fine mesh with more than 450000 quadrilateral 4-node elements.The results at the upper edge of the rectangle are shown in Figs.17 and 18.σyandτxyhave been prescribed over the upper edge as boundary conditions,therefore,the results foruyandσxobtained by the MFS in comparison with the FEM solution are shown in Figs.17 and 18.As it can be observed,the results obtained by the MFS are in excellent agreement with the FEM with very fine mesh.

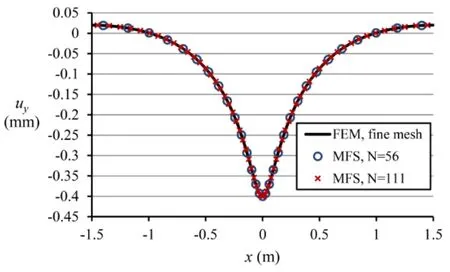
Figure 17:Vertical displacement along the upper edge of the rectangle

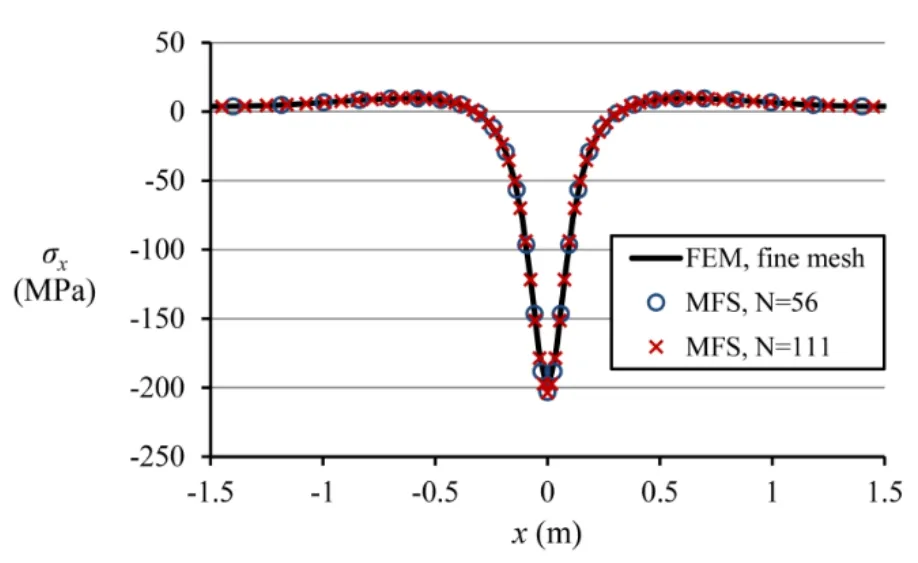
Figure 18:Normal stress in x-direction along the upper edge of the rectangle

For better investigation of the convergence rate of the FEM and the MFS,numerical results forσxat the critical point (0,0.5) with different number of finite elements and different number of collocation points are computed.For the FEM modelling of the problem,a denser mesh is used around the critical point.The discretization of the rectangle with 1200 finite elements is shown in Fig.19.The numerical results are listed in Tab.4.From this table it is observed that a large number of finite elements are required to accurately model the problem.However,it is possible to obtain very accurate solutions using the MFS with a relatively small number of collocation points.

In the previous analysis,we considered a configuration of collocation points with nonuniform spacing.For better clarification,we also examined a case with 116 collocation points and with uniform spacing as shown in Fig.20.In this case,the distance between the pseudo and main boundaries is uniform and equal to 0.285.This distance has been found by solving an optimization problem for minimizingEΓ(see Eq.(36)).The obtained value forσxat point (0,0.5) in this case is -191.8 MPa.Comparing this value with those reported in Tab.4,it is observed that the results obtained by the configurations with non-uniform spacing of collocation points are much better than the case with uniform spacing between collocation points.

Figure 19:Discretization of the rectangle using 1200 finite elements

Table 4:Normal stress in x-direction at the critical point of the rectangle with different number of elements/collocation points

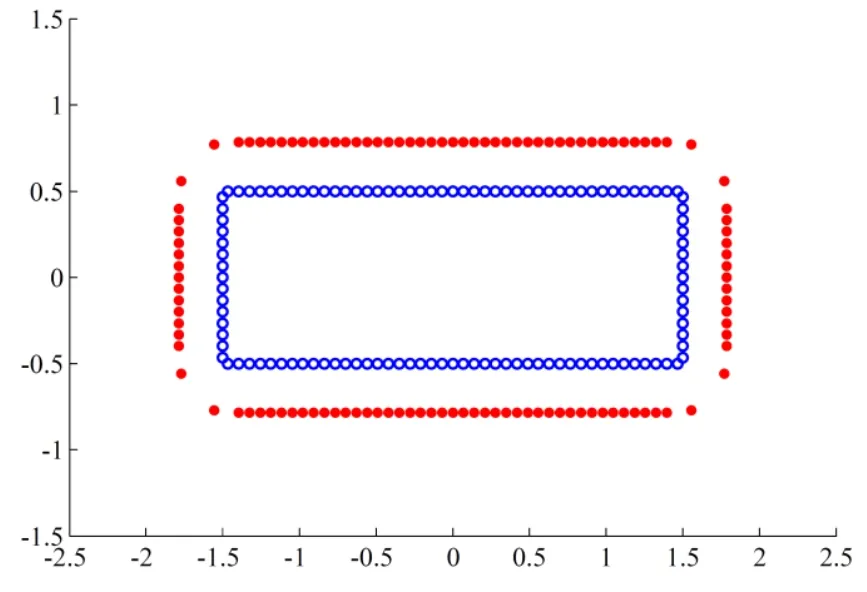
Figure 20:Configuration of 116 collocation points with uniform spacing and 116 source points with uniform distance from the main boundary

7 Conclusions

In this work,by a numerical study,the effects of the distance between pseudo and main boundaries in the MFS for 2D elastostatic problems were investigated.It was observed that in the cases where the source points were near to the main boundary,the obtained solutions for displacements and stresses had unacceptable oscillations on the boundary.It was suggested to locate the source points in a way that their location parameters would be greater than 0.85.

Greater values of the location parameter results in more smooth solutions;however,it makes the resulting system of equations ill-conditioned.To solve the ill-conditioned system of equations,the TSVD with a criterion based on the accuracy of imposition of boundary conditions was employed.The solutions of elastostatic problems obtained by the MFS exactly satisfy the governing equations of elasticity;however,the boundary conditions are only satisfied at collocation points.By making sure that boundary conditions are also accurately satisfied at some test points between collocation points,we can obtain very accurate solutions.

In real engineering elastostatic problems,the values of the elastic constants are very large and the values of displacements are very small.This is another reason for making the system of equations ill-conditioned.A procedure for normalizing the shear modulus was suggested in this work and it was observed that it is very effective in reducing the condition number of the system of equations and improving the results.

It was found that problems involving tractions with a local concentration on the boundary can be suitably modeled and accurately solved by the MFS.In these cases,one can consider condensed collocation points near the critical point on the boundary.The spacing between collocation points should be gradually changed from a small value at the critical point to a larger value at the other parts of the boundary.We can use a specific value of the location parameter (e.g.,K=0.95) for source points around the critical point.By this approach,the source points around the critical points would be closer to the boundary (see Figs.15 and 16).

The results of the presented numerical examples showed that by considering the remarks made in this work,we are able to accurately solve very complicated 2D elastostatic problems using the MFS with a small number of collocation points.Since the MFS is a boundary-type truly meshfree method,it can be efficiently used for analysis of shape and structural optimization problems.It should be mentioned that the application of the presented method to three-dimensional problems is not straightforward and needs more investigations.

References

Alves,C.J.(2009):On the choice of source points in the method of fundamental solutions.Engineering Analysis with Boundary Elements,vol.33,no.12,pp.1348-1361.

Askour,O.;Tri,A.;Braikat,B.;Zahrouni,H.;Potier-Ferry,M.(2018);Method of fundamental solutions and high order algorithm to solve nonlinear elastic problems.Engineering Analysis with Boundary Elements,vol.89,pp.25-35.

Berger,J.R.;Karageorghis,A.(2001):The method of fundamental solutions for layered elastic materials.Engineering Analysis with Boundary Elements,vol.25,no.10,pp.877-886.

Chen,C.S.;Cho,H.A.;Golberg,M.A.(2006):Some comments on the illconditioning of the method of fundamental solutions.Engineering Analysis with Boundary Elements,vol.30,no.5,pp.405-410.

Chen,C.S.;Karageorghis,A.;Li,Y.(2016):On choosing the location of the sources in the MFS.Numerical Algorithms,vol.72,no.1,pp.107-130.

Chen,J.S.;Yoon,S.;Wu,C.T.(2002):Non-linear version of stabilized conforming nodal integration for Galerkin mesh-free methods.International Journal for Numerical Methods in Engineering,vol.53,no.12,pp.2587-2615.

De Medeiros,G.C.;Partridge,P.W.;Brandão,J.O.(2004):The method of fundamental solutions with dual reciprocity for some problems in elasticity.Engineering Analysis with Boundary Elements,vol.28,no.5,pp.453-461.

Fam,G.S.;Rashed,Y.F.(2005):The Method of Fundamental Solutions applied to 3D structures with body forces using particular solutions.Computational Mechanics,vol.36,no.4,pp.245-254.

Feng,G.;Li,M.;Chen,C.S.(2014):On the ill-conditioning of the MFS for irregular boundary data with sufficient regularity.Engineering Analysis with Boundary Elements,vol.41,pp.98-102.

Golub,G.H.;Heath,M.;Wahba,G.(1979):Generalized cross-validation as a method for choosing a good ridge parameter.Technometrics,vol.21,no.2,pp.215-223.

Gorzelańczyk,P.;Kołodziej,J.A.(2008):Some remarks concerning the shape of the source contour with application of the method of fundamental solutions to elastic torsion of prismatic rods.Engineering Analysis with Boundary Elements,vol.32,no.1,pp.64-75.

Grabski,J.K.(2019):On the sources placement in the method of fundamental solutions for time-dependent heat conduction problems.Computers &Mathematics with Applications(In Press).

Grabski,J.K.;Karageorghis,A.(2019):Moving pseudo-boundary method of fundamental solutions for nonlinear potential problems.Engineering Analysis with Boundary Elements,vol.105,pp.78-86.

Gu,Y.;Fan,C.M.;Xu,R.P.(2019):Localized method of fundamental solutions for large-scale modeling of two-dimensional elasticity problems.Applied Mathematics Letters,vol.93,pp.8-14.

Hansen,P.C.(1992):Analysis of discrete ill-posed problems by means of the Lcurve.SIAM Review,vol.34,no.4,pp.561-580.

Hansen,P.C.;O’Leary,D.P.(1993):The use of the L-curve in the regularization of discrete ill-posed problems.SIAM Journal on Scientific Computing,vol.14,no.6,pp.1487-1503.

Hematiyan,M.R.;Haghighi,A.;Khosravifard,A.(2015):A method for appropriate determination of the location of sources in the method of fundamental solutions.16thInternational Conference on Boundary Element and Meshless Techniques.

Hematiyan,M.R.;Haghighi,A.;Khosravifard,A.(2018):A two-constraint method for appropriate determination of the configuration of source and collocation points in the method of fundamental solutions for 2D Laplace equation.Advances in Applied Mathematics and Mechanics,vol.10,no.3,pp.554-580.

Hematiyan,M.R.;Khosravifard,A.;Liu,G.R.(2014) A background decomposition method for domain integration in weak-form meshfree methods.Computers &Structures,vol.142,pp.64-78.

Jamshidi,B.;Hematiyan,M.R.;Mahzoon,M.(2019) An improved time domain meshfree method for analysis of quasi-static and dynamic inhomogeneous viscoelastic problems.Engineering Analysis with Boundary Elements,vol.106,pp.59-67.

Karageorghis,A.(2009):A practical algorithm for determining the optimal pseudoboundary in the method of fundamental solutions.Advances in Applied Mathematics and Mechanics,vol.1,no.4,pp.510-528.

Li,M.;Chen,C.S.;Karageorghis,A.(2013):The MFS for the solution of harmonic boundary value problems with non-harmonic boundary conditions.Computers &Mathematics with Applications,vol.66,no.11,pp.2400-2424.

Li,Z.C.;Lee,M.G.;Huang,H.T.;Chiang,J.Y.(2017):Neumann problems of 2D Laplace’s equation by method of fundamental solutions.Applied Numerical Mathematics,vol.119,pp.126-145.

Liu,C.S.(2008):Improving the ill-conditioning of the method of fundamental solutions for 2D Laplace equation.Computer Modeling in Engineering &Sciences,vol.28,no.2,pp.77-93.

Liu,C.S.(2012):An equilibrated method of fundamental solutions to choose the best source points for the Laplace equation.Engineering Analysis with Boundary Elements,vol.36,no.8,pp.1235-1245.

Liu,C.;Wang,F.;Qu,W.(2018):Fast solving the cauchy problems of poisson equation in an arbitrary three-dimensional domain.Computer Modeling in Engineering &Sciences,vol.114,no.3,pp.351-380.

Liu,X.;Shao,G.;Yue,X.;Yang,Q.;Su,J.(2018).A virtual boundary element method for three-dimensional inverse heat conduction problems in orthotropic media.Computer Modeling in Engineering &Sciences,vol.117,no.2,pp.189-211.

Marin,L.;Lesnic,D.(2004):The method of fundamental solutions for the Cauchy problem in two-dimensional linear elasticity.International Journal of Solids and Structures,vol.41,no.13,pp.3425-3438.

Marin,L.(2005):A meshless method for solving the Cauchy problem in threedimensional elastostatics.Computers &Mathematics with Applications,vol.50,no.1-2,pp.73-92.

Marin,L.;Karageorghis,A.(2013a):The MFS-MPS for two-dimensional steady-state thermoelasticity problems.Engineering Analysis with Boundary Elements,vol.37,no.7-8,pp.1004-1020.

Marin,L.;Karageorghis,A.(2013b):The MFS for the Cauchy problem in twodimensional steady-state linear thermoelasticity.International Journal of Solids and Structures,vol.50,no.20-21,pp.3387-3398.

Marin,L.;Karageorghis,A.;Lesnic,D.(2015):A numerical study of the SVD-MFS solution of inverse boundary value problems in two-dimensional steady-state linear thermoelasticity.Numerical Methods for Partial Differential Equations,vol.31,no.1,pp.168-201.

Marin,L.;Karageorghis,A.;Lesnic,D.(2016):Regularized MFS solution of inverse boundary value problems in three-dimensional steady-state linear thermoelasticity.International Journal of Solids and Structures,vol.91,pp.127-142.

Mohammadi,M.;Hematiyan,M.R.;Khosravifard,A.(2019):Analysis of two- and three-dimensional steady-state thermo-mechanical problems including curved line/surface heat sources using the method of fundamental solutions.European Journal of Computational Mechanics,vol.28,no.1-2,pp.51-80.

Poullikkas,A.;Karageorghis,A.;Georgiou,G.(2002):The method of fundamental solutions for three-dimensional elastostatics problems.Computers &structures,vol.80,no.3,pp.365-370.

Ramachandran,P.A.(2002):Method of fundamental solutions:singular value decomposition analysis.Communications in Numerical Methods in Engineering,vol.18,no.11,pp.789-801.

Sadd,M.H.(2009):Elasticity:Theory,Applications,and Numerics.Academic Press.

Sun,Y.;Marin,L.(2017):An invariant method of fundamental solutions for twodimensional isotropic linear elasticity.International Journal of Solids and Structures,vol.117,pp.191-207.

Tsai,C.C.;Lin,Y.C.;Young,D.L.;Atluri,S.N.(2006):Investigations on the accuracy and condition number for the method of fundamental solutions.Computer Modeling in Engineering &Sciences,vol.16,no.2,pp.103-114.

Tsai,C.C.;Young,D.L.(2013):Using the method of fundamental solutions for obtaining exponentially convergent Helmholtz eigensolutions.Computer Modeling in Engineering &Sciences,vol.94,no.2,pp.175-205.

Tsai,C.C.(2009):The method of fundamental solutions with dual reciprocity for threedimensional thermoelasticity under arbitrary body forces.Engineering Computations,vol.26,no.3,pp.229-244.

Wong,K.Y.;Ling,L.(2011):Optimality of the method of fundamental solutions.Engineering Analysis with Boundary Elements,vol.35,no.1,pp.42-46.

Zhang,A.;Gu,Y.;Hua,Q.;Chen,W.;Zhang,C.(2018):A regularized singular boundary method for inverse Cauchy problem in three-dimensional elastostatics.Advances in Applied Mathematics and Mechanics,vol.10,no.5,pp.1459-1477.