The Multi-Horizon Peridynamics

Ali Jenabidehkordia nd Timon Rabczuk,

1Division of Computational Mechanics,Ton Duc Thang University,Ho Chi Minh,Vietnam.

2Faculty of Civil Engineering,Ton Duc Thang University,Ho Chi Minh,Vietnam.

Abstract:We present a novel refinement approach in peridynamics (PD).The proposed approach takes advantage of the PD flexibility in choosing the shape of the horizon by introducing multiple domains (with no intersections) to the nodes of the refinement zone.We will show that no ghost forces are needed when changing the horizon sizes in both subdomains.The approach is applied to both bond-based and state-based peridynamics and verified for a simple wave propagation refinement problem illustrating the efficiency of the method.

Keywords:Peridynamics,variable horizon size,multi-horizon,ghost force,wave reflection,refinement.

1 Introduction

Peridynamics has initially been introduced by Silling [Silling (2000)].The initial bondbased peri- dynamics (BB-PD) has been extended later on to the so-called state-based peridynamics (SB-PD) approaches [Silling,Epton,Weckner et al.(2007)].In contrast to BB-PD,SB- PD allows for general constitutive models.PD can be regarded as a nonlocal extension of classical continuum mechanics.One key application of PD is modeling material failure though the method has been meanwhile applied to other fields,see e.g.,the contributions in Oterkus et al.[Oterkus,Madenci and Agwai (2014),Bobaru and Duangpanya (2012);Diyaroglu,Oterkus,Oterkus et al.(2015)].PD has meanwhile been implemented into open-source software such as LAMMPS [Parks,Seleson,Plimpton et al.(2011)],which is a software for Molecular Dynamics (MD) simulations.

The “standard” PD requires a fixed horizon size over the whole domain yielding high computational cost.The approaches presented in the work of Dipasquale et al.[Dipasquale,Zaccariotto and Galvanetto (2014)] allow for variable horizon sizes but introduce so-called ghost forces which lead to artificial wave reflections between domains of different horizon sizes.An elegant solution that avoids ghost forces is dual-horizon peridynamics (DH-PD) [Ren,Zhuang,Cai et al.(2016),Ren,Zhuang and Rabczuk (2017)].Other contributions dealing with improving the computational efficiency of PD have been proposed,for instance,by Pasetto et al.[Pasetto,Leng,Chen et al.(2018)] or by Lindsay et al.[Lindsay,Parks and Prakash (2016)].In this manuscript,we present another simple alternative to deal with multiple horizon sizes.The next section describes the basic idea of the refinement approach including advantages and disadvantages.Examples are presented in Section 3 before Section 4 concludes the manuscript.

2 Multi-horizon peridynamics

The PD equations of motion theoretically introduce no limitation on the integration over their horizon [Silling (2000)].In this article,we are proposing a change of the horizon shapes for nodes in the interaction regions between domains with different horizon sizes.

The PD domain can be refined utilizing the “standard” formulation,which requires a fixed spherical horizon with a constant radius.The refinement cost will increase by the neighborhood size,which is exponentially increasing by the refinement factor (the difference between refined and coarse subdomains).

Employing different horizon radii will lead to erroneous results or even instabilities due to ghost forces as illustrated in Fig.1,where a subdomain at a position X has a horizon radius of R and its neighbor at X’ has a horizon radius of r,where R＞r and r＜|X-X’|＜R;X will include X’ in its neighborhood but will not be included in the X’ neighborhood.Thus,X will have a force toward X’ (i.e.,ghost force) without X’ having any force towards X,causing an imbalance in the bond between X and X’.

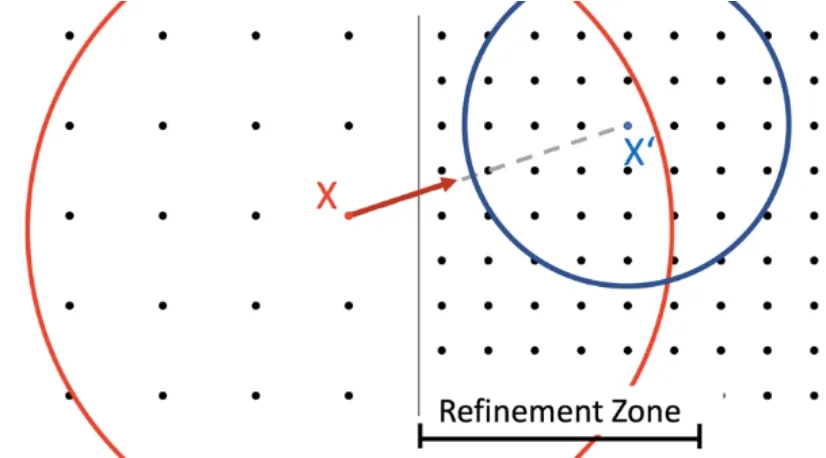
Figure 1:The appearance of the ghost force at the refinement bound

For the sake of simplicity,let us assume refinement occurs along a straight line,as illustrated in Fig.2.The proposed approach suggests enforcing the symmetry of the interaction nodes having different horizon sizes by forcing all the nodes to include themselves to all of their neighbor nodes.For instance,x’ in Fig.2(a) will include all volumes of the subdomains in which x’ is included (e.g.,x in Fig.2(a)).Thus,the nodes in the refined domain may have more than one horizon.Note that the interaction between the domains is a one to one relation,thus multi-horizons of the refined nodes cannot coincide.Let us call the part of the multi-horizon that has the same radius as those of refined nodes as the natural horizon (Hn),and the rest of the multi-horizon as the interaction horizon (Hi).

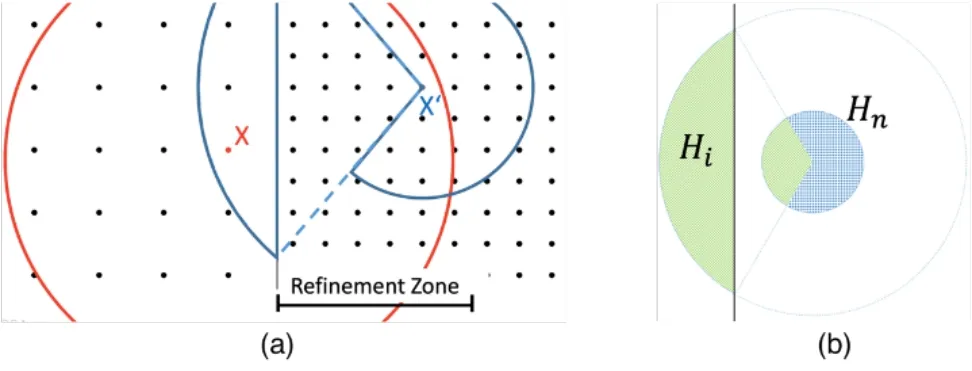
Figure 2:a) The proposed horizons for nodes inside the refinement zone,b) multi-horizon of a node inside the refined domain (Hi:interaction horizon,Hn:natural horizon)

Fig.2(a) illustrates the horizons of two nodes on the refinement zone,x,and x’,while Fig.2(b) presents the natural horizon and interaction horizon of the refined node.Outside of the refinement zone,multi-horizons do not affect the PD equation of motion which can be written for each point of domain positioned at x and a node x’ inside its horizon H in the global form of

where ρ,b,and u are the density,the body force,and the displacement of the center of x’s horizon respectively.Note,that equation 1 is valid for all PD-types,i.e.,bond-based (BBPD),ordinary state-based (OSB-PD),and non-ordinary state-based (NSB-PD) peridynamics.Let us consider the force vector state T.Its relation to the deformed direction vector state M is given as

Eq.(1) within the refinement zone can be written as

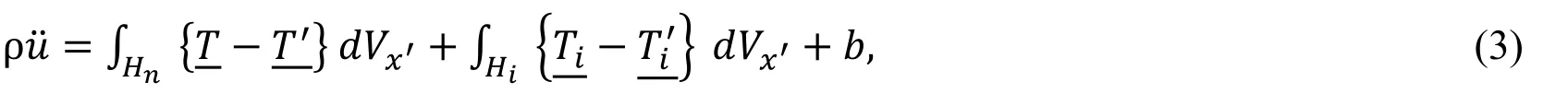
where Tis are the force vector state for the interaction horizon andhas to be defined in a way that Eq.(1),and Eq.(3) have one to one equivalent integral functions on their righthand side.In other words,the multi-horizon formulation has to provide the same acceleration as if the whole domain was refined.This requires

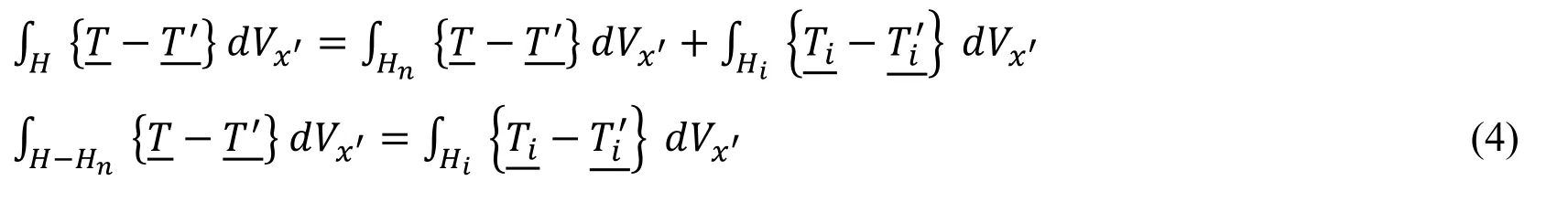
where H-Hnis the difference between the “standard” horizon and the natural horizon,which is a subset of the interaction horizon since it still has no intersections with the natural horizon.Rewriting Eq.(2) for Tiand utilizing the deformed direction vector state,we obtain

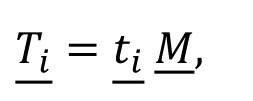
Thus,

Substituting Eq.(5) into Eq.(6)

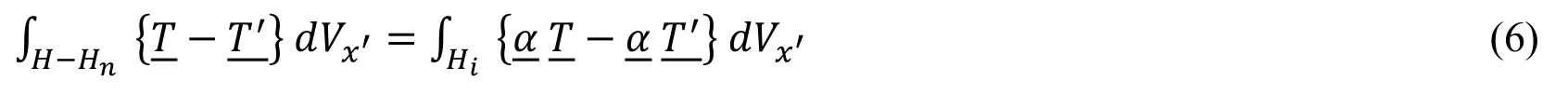
where the only unknown parameter is α,which can be easily computed having the interaction horizon and its equivalent horizon in case of refining the whole domain (H-Hn).Note that α remains time-independent and therefore,it needs to be computed only at the initial configuration.It is also worth mentioning that NSP-PD can also be implemented as a multihorizon method if Eq.(6) is satisfied.If the refined node is located within a finite number of refinement zones,Eq.(7) can be utilized for each of the interaction horizons individually.

2.1 Absence of ghost forces

Ghost forces occur due to violation of Newton’s law,which is the case for unsymmetrical interactions of particles,which commonly occur for nodes with different horizon sizes.This is also possible for un-symmetric or dissimilar shapes of the horizons.For models with only spherical horizon shapes for all sub-domains,only differences in the horizon radius between two sub-domains can cause ghost forces in the refinement zone.Multihorizons guarantee the existence of the nodes inside the domain with larger horizon radii,which eliminates ghost forces.

2.2 Numerical implementation

Implementing the concept of multi-horizons into an existing PD-code requires three changes:

1.At the initial configuration,the nodes in the refinement zone have to be determined.

2.The parameter α(s) for each node located inside refinement zone should be determined.Note that neighbor nodes may share their representative volume with more than one horizon.

3.After computing the bond forces,the forces of the interaction horizons have to be multiplied with α.

Implementing the first two changes usually requires the modification of the data structure in which the horizons and their neighbors are stored.

3 Numerical example

The computation of α can be cumbersome for complex refinement zones,especially in 2D and 3D,as the intersections of the associated volumes of the neighboring nodes may demand complex geometry computations.For the sake of simplicity,we,present a simple 1D example to demonstrate the performance of the multi-horizon approach.Consider a 1D bar of length 100 mm and two fixed ends applied to a velocity wave excitation in the middle of the bar,as illustrated in Fig.3.The two ends of the bar have a node distance of 0.1 mm.The distance between nodes and the horizon radius in the middle of the bar is four-time bigger than the ends.The velocity wave has an exponential equation of v =e-0.03(x-0.05)2m/s.

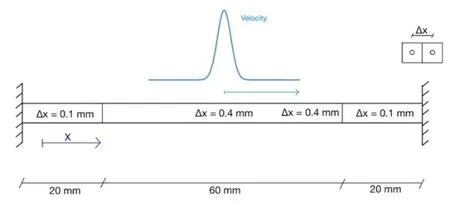
Figure 3:Initial configuration of the numerical example

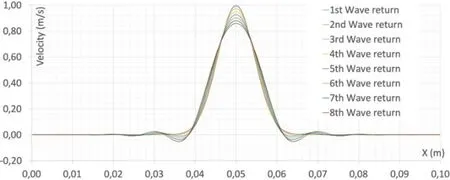
Figure 4:The first eight returned velocity waves for the bar in Fig.3

To study the artificial wave reflection added by refinement zone,the response of the bar is recorded whenever the displacement of the mid node arrives at its peak.Fig.4 presents the first eight returned velocity waves.The artificial wave reflection due to the refinement zone is relatively small.As illustrated in Fig.5,the maximum error of 15% is observed after the eights wave reflection.

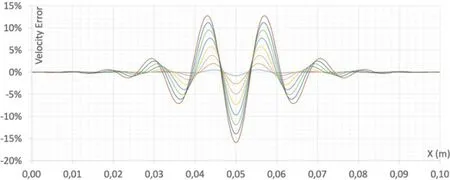
Figure 5:The velocity error of waves in Fig.4 compare to the non-refined bar (Colors are the same as Fig.4)

Let us consider now a 0.2 mm node distance in the middle and 0.05 mm node distance at the two ends of the bar.The velocity and its error after the eight wave reflection can be found in Figs.6 and 7,respectively.

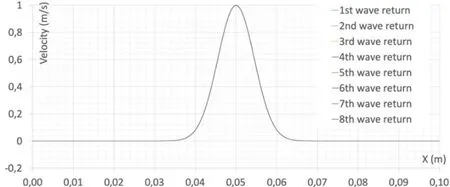
Figure 6:The first eight returned velocity waves for a bar similar to the bar Fig.3 with half of the node distance

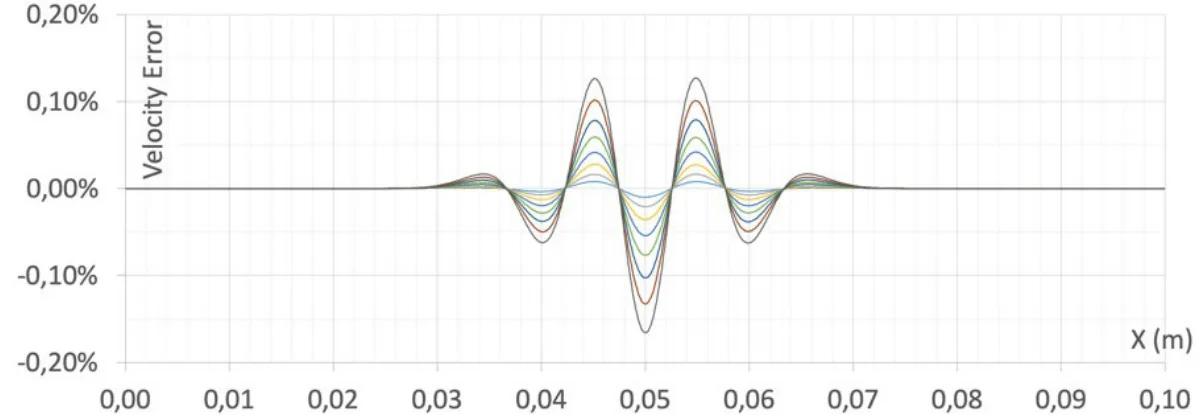
Figure 7:The velocity error of waves in Fig.6 compare to the non-refined bar (Colors are the same as Fig.6)

Finally,we test a pulse excitation on the same bar (see Fig.3) where the node distances are 0.05,and 0.2 mm at the end and middle,respectively.Fig.8 illustrates the first eight wave reflections.Although the error is about 40%,the simulation still remains stable.Note that this error is expected as PD is not well suited for capturing such sharp wave shapes.

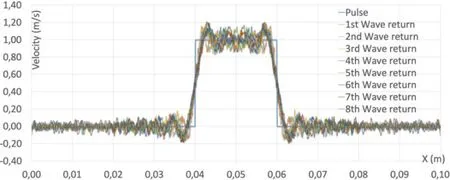
Figure 8:The first eight returned velocity waves for a bar similar to the bar Fig.3 with a pulse excitation

4 Conclusions

A simple approach for PD with variable horizons is proposed,which is important for computational efficiency.The approach avoids ghost forces and related artificial wave reflections.Several problems have been simulated utilizing the proposed method.In summary:

• The proposed model can be used in the interaction of any finite number of domains with different node distances and horizon sizes.

• The method eliminates the existence of any ghost forces.

• The implementation of the method has almost no effect on the computational cost,and only demands changes in the initiation of the domain(s) configuration.

On the downside,the implementation of the method in 2D and 3D requires complex geometrical solver.However,such solvers are open-source and can be combined with the proposed scheme.

References

Bobaru,F.;Duangpanya,M.(2012):A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities.Computational Physics,vol.231,no.7,pp.2764-2785.

Dipasquale,D.;Zaccariotto,M.;Galvanetto,U.(2014):Crack propagation with adaptive grid refinement in 2D peridynamics.Fracture,vol.190,no.1-2,pp.1-22.

Diyaroglu,C.;Oterkus,E.;Oterkus,S.;Madenci,E.(2015):Peridynamics for bending of beams and plates with transverse shear deformation.Solids and Structures,vol.69,pp.152-168.

Lindsay,P.;Parks,M.;Prakash,A.(2016):Enabling fast,stable and accurate peridynamic computations using multi-time-step integration.Computer Methods in Applied Mechanics and Engineering,vol.306,pp.382-405.

Oterkus,S.;Madenci,E.;Agwai,A.(2014):Fully coupled peridynamic thermomechanics.Mechanics and Physics of Solids,vol.64,pp.1-23.

Parks,M.L.;Seleson,P.;Plimpton,S.J.;Silling,S.A.;Lehoucq,R.B.(2011):Peridynamics with LAMMPS:a user guide,v0.3 beta.Sandia Report,pp.1-34.

Pasetto,M.;Leng,Y.;Chen,J.S.;Foster,J.T.;Seleson,P.(2018):A reproducing kernel enhanced approach for peridynamic solutions.Computer Methods in Applied Mechanics and Engineering,vol.340,pp.1044-1078.

Ren,H.;Zhuang,X.;Cai,Y.;Rabczuk,T.(2016):Dual-horizon peridynamics.Numerical Methods in Engineering,vol.108,no.12,pp.1451-1476.

Ren,H.;Zhuang,X.;Rabczuk,T.(2017):Dual-horizon peridynamics:a stable solution to varying horizons.Computer Methods in Applied Mechanics and Engineering,vol.318,pp.762-782.

Silling,S.A.(2000):Reformulation of elasticity theory for discontinuities and long-range forces.Mechanics and Physics of Solids,vol.48,no.1,pp.175-209.

Silling,S.A.;Epton,M.;Weckner,O.;Xu,J.;Askari,E.(2007):Peridynamic states and constitutive modeling.Journal of Elasticity,vol.88,no.2,pp.151-184.