Peridynamic Modeling and Simulation of Ice Craters By Impact

Ying Song,Jiale Yan,Shaofan Li, and Zhuang Kang

1College of Shipbuilding Engineering,Harbin Engineering University,Harbin,150001,China.

2Department of Civil and Environmental Engineering,University of California,Berkeley,CA,USA.

Abstract:In the present work,a state-based peridynamics with adaptive particle refinement is proposed to simulate water ice crater formation due to impact loads.A modified Drucker-Prager constitutive model was adopted to model ice and was implemented in the state-based peridynamic equations to analyze the elastic-plastic deformation of ice.In simulations,we use the fracture toughness failure criterion in peridynamics to simulate the quasi-brittle failure of ice.An adaptive particle refinement method in peridynamics was proposed to improve computational efficiency.The results obtained using the peridynamic model were compared with the experiments in previous literatures.It was found that the peridynamic simulation results and the experiments matched well except for some minor differences discussed,and the state-based peridynamic model has shown the specific predictive capacity to capture the detailed crater features of the ice.

Keywords:Peridynamics,ice constitutive model,adaptive particle refinement,ice craters,impact.

1 Introduction

Studying the behavior of ice under high-velocity impact can be encountered in civil engineering,shipbuilding,arctic research,and aerospace missions [Gao,Hu and Wang (2014);Liu,Xue,Lu et al.(2014);Poelchau,Kenkmann,Hoerth et al.(2014)].Although many methods have been used to conduct research on ice behavior by impact,it is still a challenging task in computational mechanics research.The impact craters in ice can provide an understanding of the ice behavior due to impact [Gao,Hu and Wang (2014)].There are two main approaches to capture the features of ice craters,modeling and laboratory testing.One of them is successfully done using the hydrodynamic code CTH,which produces a state Mie-Gruniesen formulation for ice [Jesse (2010)] to perform computer simulations.However,the modeling contains assumptions as to the physics involved [Shrine (2004)].The process of ice behavior under impact remains incomprehension due to the complexity of ice physical properties including the density,the temperature,the porosity,the salinity,and the strain rate.This makes it a critical issue to select the ice constitutive model.Furthermore,the damage of ice presents a discontinuity process during the impact that involves difficulties in solving such problems by traditional simulation methods came out of classical continuum mechanics [Peng,Zhang and Ming (2018)].Although laboratory crating experiments [Cui,Zhang,Wang et al.(2018)] have many advantages in examining the ice material,it still has limitations in the processing of the ice cratering test involving size scale.

Peridynamic theory,which was proposed by Silling et al.[Silling and Askari (2005)],is a non-local computational continuum mechanical method [Kundu (2018);Madenci (2004)].The mechanical behaviors of ice during impact in solids can be characterized by its ability to capture discontinuous deformations along the cracks [Ha and Bobaru (2011)].Efforts have been made to simulate ice behaviors by using peridynamics in recent years.Wang et al.[Wang,Wang and Zan (2018)] applied peridynamic theory to simulate the ice fragmentation subjected to underwater explosive loads.Based on bond-based peridynamics,the ice was built by an elastic-brittle constitutive model.Liu et al.[Liu,Wang and Lu (2017)] studied the force of a rigid cylindrical structure interacted on the ice based on state-based peridynamics.

Moreover,peridynamic simulations [Bergel and Li (2016)] are usually performed with a constant horizon and are used as a uniform particle distribution.In some cases,especially to simulate the ice craters in 3D [Lange and Ahrens (1981)],the number of particles discretized in peridynamics is too large to use as a uniform particle distribution [Rabczuk,Ren and Zhuang (2019)] and may become forbidden from the perspective of memory requirements.In terms of this issue,using an adaptive particle refinement method may become a reasonable solution [Ren,Zhuang,Cai et al.(2016);Ren,Zhuang and Rabczuk (2017);Ren,Zhuang and Rabczuk (2018)].Bobaru et al.[Bobaru and Ha (2011)] proposed an adaptive refinement algorithm based on bond-based peridynamic model that is capable of solving two-dimension statics problems.Furthermore,adaptive grid refinement adopted by Dipasquale et al.[Dipasquale,Zaccariotto and Galvanetto (2014)] was used to study the dynamic crack propagation in two-dimensional brittle materials.

Unlike the previous work,the present study concludes the following processes:(1) A modified Drucker-Prager model was developed [Drucker and Prager (1952)] and was implemented into the corresponding peridynamic equations to simulate ice elastic-plastic behaviors.(2) Focusing on the ice craters simulation,an ice particle decohesion criterion was adopted to capture the brittle failure of ice.(3) The technique of adaptive particle refinement was used to investigate the ice craters,due to the reduction in the cost of the CPU time and memory requirements.Moreover,the test case was used to demonstrate the proposed adaptive particle refinement method.(4) A peridynamic contact algorithm was used to model the contact between the rigid projectile and ice targets.

Our present paper is organized into the following five sections:(a) In Section 2,the state-based peridynamic theory and introduction of the updated artificial viscosity are overviewed.(b) In Section 3,the ice material properties and the proposed modified Drucker-Prager model are prescribed,with the criteria of ice failure based on peridynamics.(c) In Section 4,a numerical implementation process is introduced to model ice behaviors,mainly focusing on the implementation of the constitutive updates into corresponding peridynamic formulations.Furthermore,the contact algorithm and adaptive particle refinement theory are introduced in this Section.(d) In Section 5,the numerical simulation of ice craters by impact is discussed as well as the parametric study of ice craters,and then used to compare with the corresponding experiments.(e) In Section 6,the numerical results of the study drawn some conclusions,and made significant closing remarks.

2 The state-based peridynamic formulation overview

In this Section,the state-based peridynamic method is briefly introduced.Then the integration of the artificial viscosity is presented,which is developed by Monaghan [Liu and Liu (2003)] into the peridynamic formulation.

2.1 State-based peridynamic theory

Peridynamics was proposed by using the non-local mechanical theory with its equations of motion replacing general partial differential derivatives with displacement,including integral formulations [Silling (2005)].Stated-based peridynamics has an apparent advantage in simulating ice fragmentation.In the state-based peridynamic theory,0Ω as a continuum domain can discretize into material particle xiwith the related mass densityρxiand volumeVi(wherei= 1,2,…,∞ denotes the index of the particle).Assume that a material particle xiis only affected by the forces from its neighboring particles xj(j= 1,2,…,∞) within its local region known as a horizonHx(i)and illustrated in Fig.1.The horizon was typically chosen with the radiusδ,known as the horizon diameter of the particle xi.The relative position vector is called “bond,” which points from one particle xito its neighboring particle xj,and can be considered as an elastic spring due to the interaction (as shown in Fig.1).This is denoted as

The continuum body deforms under specific deformationχ,and the bond in the current configuration is indicated by

The current relative position vector between particle xiand xjis then described by the deformation state functionwhich maps the undeformed relative position vector to a deformed relative position vector:

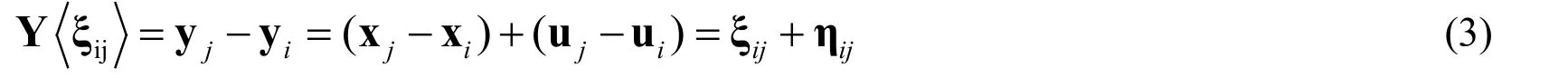
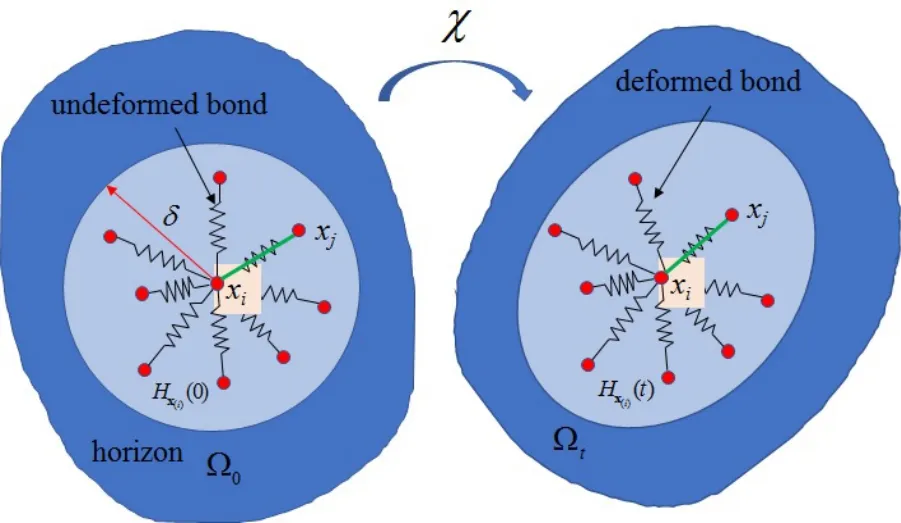
Figure 1:Sketch of the bond in state-based Peridynamics [Fan and Li (2016)]

At a reference configuration,the peridynamic governing equation of motion for a particle xiat timet[Madenci and Oterkus (2014)] can be denoted as

whereρ0is the mass density of the continuum body;f ( ηij,ξij) is a pairwise function defined as the non-local integration of force vector that the particle xjexerts on the particle xi(as shown in Fig.1);and b ( xi,t) is the external body force density vector (as shown in Eq.(4)).Such non-local formulation contributes toward peridynamics to be adequate to perform discontinuity everywhere.

In the state-based peridynamic theory,one concern is the force state T besides the deformation state Y.The momentum balance equation with the force state T can be expressed as

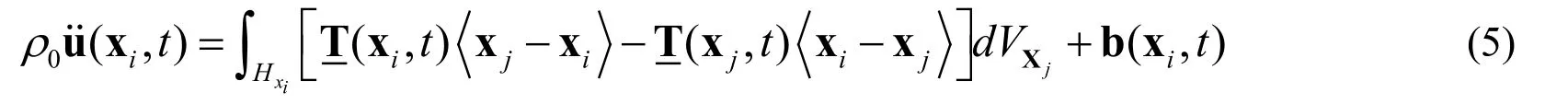
In the present work,the state-based peridynamic theory considered strain-rate effects into account,and the following governing equation can be obtained:

According to the classical continuum mechanics,the relationship between the force-vector state T and the first Piola-Kirchhoff stress tensor Pxi[Silling,Epton,Weckner et al.(2007)] can be expressed as

In whichω(ξij)is a positive scalar influence function can be represented by the length of each bond ξij;and Kxiis the symmetric shape tensor [Fan and Li (2017)] of the particle xiin the reference configuration,which can be defined as

In the case of the horizon size,it is the same between the particle xiand the particle xj.Assuming that the deformations of each bond ξijare uniform within the horizon Hxi,we have Kxi=Kxj.

The relation between Pxiand Cauchy stress σxiis given by

where Fxiis the non-local deformation gradient.We first obtain the deformation gradient tensor Fxito get the first Piola-Kirchhoff stress Pxi.Therefore,a non-local two-point shape tensor Nxiis introduced as follows:

For quasi-uniform particle distributions [Lai,Liu,Li et al.(2018)],the relative deformed bonds can be written as

where Fxiis a second-order tensor,which is the approximated deformation gradient.Then we get

Then the nonlocal deformation gradient Fxican be defined at the particle xiin terms of the shape tensors as

2.2 Artificial viscosity updated

Considering large deformation problems,non-physical deformation modes may occur in the stated-based peridynamic simulations [Silling and Askari (2005)].Different treatments are required to simulate ice fragmentation that takes the strain rate into consideration.Otherwise,the simulation will develop unphysical penetration for particles approaching each other [Wang,Zhang,Ming et al.(2019)].A numerical method is proposed in the present work,which the peridynamic formulation modified with an added artificial viscous stress term.To do so,the Monaghan type artificial viscosity in Smoothed Particle Hydrodynamics [Liu and Liu (2003);Zhang,Sun,Ming et al.(2017)] is expressed as follows:

where

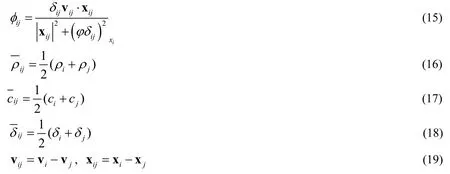
whereαΠandβΠare constants set to be 1.0,αΠgenerates a bulk viscosity,βΠis used to control particle interpenetration.0.1ϕ= is used to prevent numerical divergences.,andδijrepresent the density,the average velocity and the smoothing distance between the particles xiand xj.

The corresponding Cauchy stress [Fan and Li (2016)] can be introduced as follows:

Then,we can get the first Piola-Kirchhoff viscous stress as follows:

Finally,the force state combining with artificial viscosity function [Fan and Li (2015)] is updated as follows:

2.3 State-based peridynamic decohesion algorithm

According to the state-based peridynamic theory,when the stretching of a bond exceeds a critical values0,the bond connecting a pair of particles will break,indicating the occurrence and spread of damage.Such critical values0is called “critical bond stretch.” In order to separate the body by a fracture surface into two parts,all bonds that connecting these particles need to break initially [Madenci and Oterkus (2014)].The material constant energy release rateG0,which can reflect the crack propagation,can be derived from the fracture mechanics as follows:

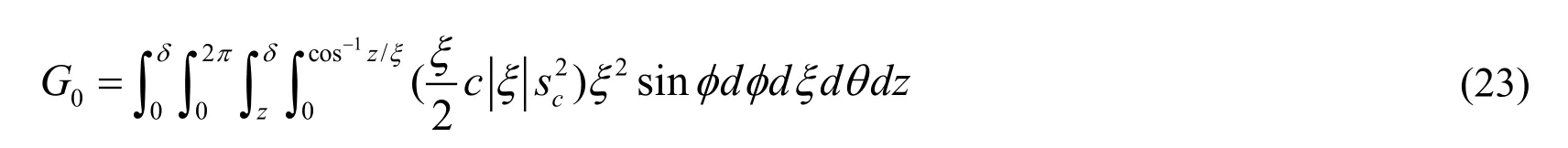
Moreover,s0can be derived as

In which,δis the radius of the horizon,E is the elasticity modulus.

The damage at a material point [Madenci and Oterkus (2014)] can be expressed as

where

3 Ice constitutive model description

The physical properties of ice are mainly affected by parameters such as temperature,porosity,salinity,and density.Ice is a special material affected by the strain rate,under the low strain rate,ice exhibits plastic properties,and under the high strain rate,ice exhibits brittle properties.Moreover,ice exerts strong behaviors under compressive conditions than in tension,which was reported by Pernas et al.[Pernas,Pedroche,Varas et al.(2019)] and Schulson [Schulson (2001)].

Many constitutive models including the Mohr-Coulomb (MC) model and the Drucker-Prager (DP) model [Drucker and Prager (1952)] have been successfully used for simulating the ice behavior.In the present work,a rate-sensitive constitutive model based on the Drucker-Prager model was proposed to simulate the ice material.

3.1 Elastic behavior

It is assumed that a hyperelastic-plastic material may model the mechanical responses of ice.The following elastic and plastic components [Rist (1997)] provide the deformation tensor:

Then adopting the expression of Hooke’s law as

In which,σ∇is an objective rate of Cauchy stress tensor;and Ceis the elastic tensor.

3.2 Inelastic behavior

To produce the inelastic behavior of the water ice,Schulson [Schulson (2001)] made the experimental observations considering the pressure dependence of strength in ice.Wang et al.[Wang and Ji (2006)] used a Drucker-Prager yield function to present the pressure dependence of ice characteristic as follows:

wherecindicates the effective cohesion;ϕindicates the effective friction angle;andpis the hydrostatic pressure expressed as

J2is the second invariant of deviatoric stress tensor defined as

s is the deviatoric stress tensor.

3.3 Failure conditions

Ice is considered to be a brittle material under the condition of an impact.G0can be expressed as [Wang,Wang and Zan et al.(2018)]

whereKIdenotes the fracture toughness,which can be measured by the experiment and reflected the resistance to the brittle fracture of ice [Liu and Miller (1979)].

Substitute Eq.(34) into Eq.(24),s0can be expressed as [Wang,Wang,Zan et al.(2018)]

4 Numerical implementations

In this Section,the numerical method to update the constitutive model of ice and the approach to implementing it into the corresponding state-based peridynamics formulations are introduced.

4.1 Explicit stress update algorithm for ice constitutive model

The non-ordinary state-based peridynamics can be regarded as a basic form of the non-local continuum theory,because the conventional relation of the stress and strain through the force-vector state T can be integrated (Eq.(7)).

The ice is treated as an ideal elastic-plastic material [Song,Yu and Kang (2018)].Drucker et al.[Drucker and Prager (1952)] put forward the yield surface and was used by Wang et al.[Wang and Ji (2006)],which was developed to simulate ice behaviors.In Section 3.2,the D-P yield function is given as mentioned.The potential plastic function of Drucker-Prager is written as follows:

whereψis the effective dilation angle.The yield function overlaps with the potential function under the condition,φ=ψ= 0.Eqs.(37) and (38) are identical,which possess advantages in presenting the ice’s shear strength.

The function of the Helmholtz free energyρΨ [Fan and Bergel (2016);Fan and Li (2017);Fan,Ren and Li (2015)] can be separated into its corresponding elastic and plastic components as

where εedenotes the elastic strain tensor;Cedenotes the elastic modulus tensor;and ζ is the set of kinematic internal state variables (ISVs) [Ren and Li (2010)].For simplicity,based on the linear softening/hardening model,the ISVs are assumed to the evolution independently.H is the softening/hardening matrix,which can be expressed as

In which,Hc,Hϕ,andHΨdenote the linear softening/hardening modulus for c,ϕ,ψ,respectively.

Rate equations for stress states and evolution equations for plastic flows [Ren,Li and Qian et al.(2011)] can be represented as follows

The developed equation of plastic flow [Liu,Amdahl and Løset (2011)] based on the potential plastic function can be expressed as following:

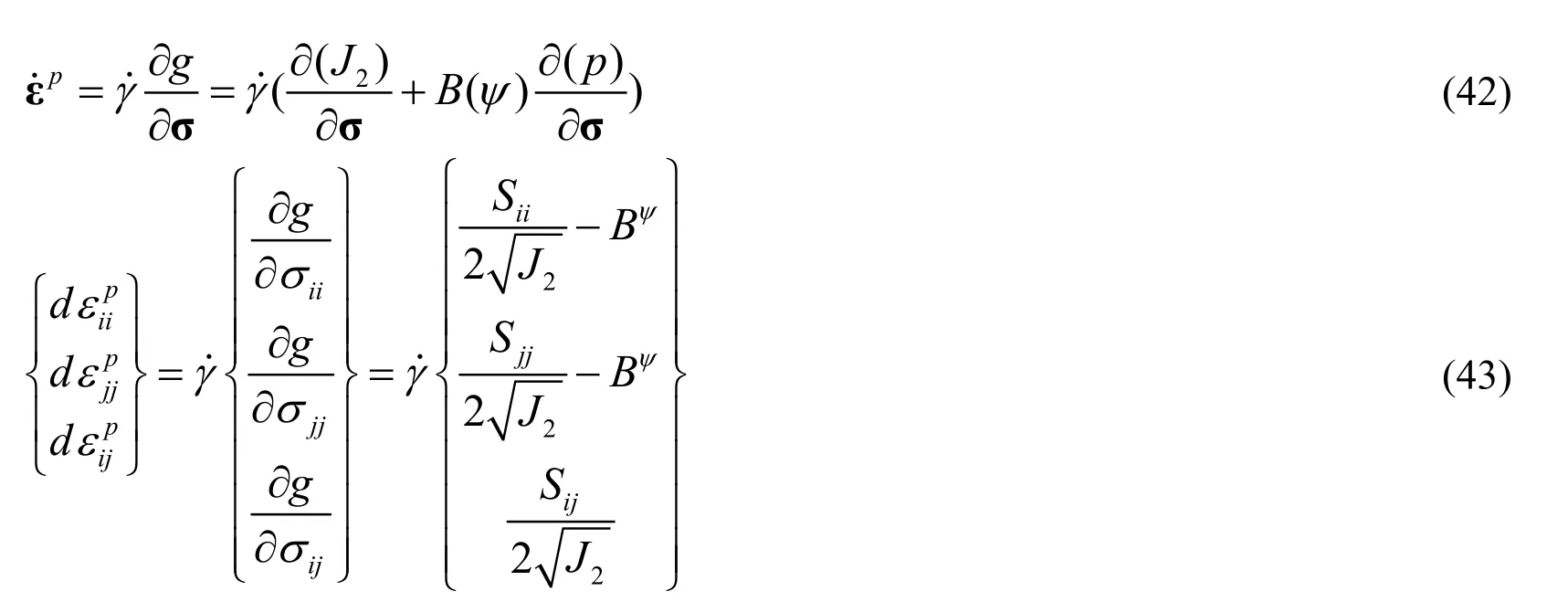
The developed equation of the ISV [Fan,Bergel and Li (2016)] can be written as

In which h is a hardening function,which can be obtained by using the maximum plastic dissipation principle:

The constitutive update equations [Fan and Li (2017)] based on the consistency condition=0 can be derived as

Based on the Newton-Raphson iteration method,the unknown sets ( σ,c,γ ) can be solved in the non-linear equations [Fan,Ren and Li (2015)].The updating algorithm is adopted as follows:

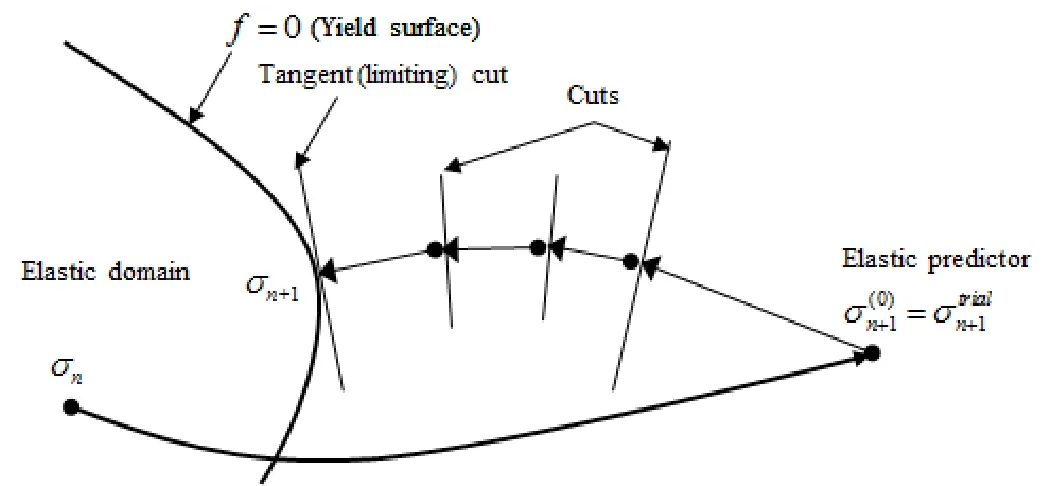
Figure 2:The direction of stress return in the yield surface [Hughes and Winget (1980)]

The trial stress is computed by Eq.(50) under small deformation assumption.However,solids such as ice subjected to high-velocity impact loads may perform large rotation deformations.Therefore,it should be replaced by a nonlinear equation of the Hughes-Winget algorithm [Hughes and Winget (1980)].In the present work,an intermediate configuration [Fan and Li (2017)] at time stepn+αcan be expressed as

whereαis a scalar and is set to be 0.5,then the deformation gradient [Fan,Bergel and Li (2016)] at the configurationxn+αis defined as

Additionally,the gradient of Δu for the reference configuration [Fan,Bergel and Li (2016)] can be represented as

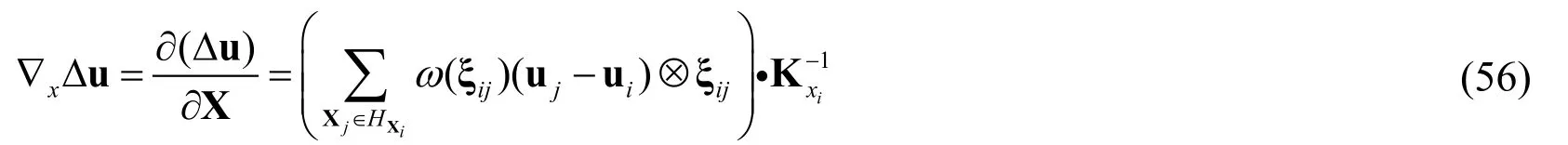
Then the deformation increment [Fan,Bergel and Li (2016)] using the chain rule can be represented as

which can be divided into the increments of strain and rotation [Fan,Bergel and Li (2016)] as follows:

Then the increment of the objective effective stress [Fan,Bergel and Li (2016)] can be written as

Finally,Eq.(49) can be replaced by a set of equations [Fan,Bergel and Li (2016)] as follows:

4.2 Contact algorithm for impact

In this work,we built a contact detection algorithm by using the penalty method [Li,Hao and Liu (2000)],which is based on the peridynamic’s frame,and then it used to be converted into peridynamics precisely due to its benefits in performing the evolution tendency [Madenci and Oterkus (2014)].In the following paragraph,the contact detection algorithm [Li,Qian,Liu et al.(2001)] and its specific implementation are introduced.

Assuming the incoming ball to be rigid and moves at a constant velocity towards the fixed solid (as shown in Fig.3(a)),the incoming ball pierce through the stationary one.It is assumed that certain static solid particles are within the range of the incoming solid particles,as shown in Fig.3(b).These particles are then squeezed out of the solid to simulate the infiltration physical process,as shown in Fig.3(c).The practical contact algorithm is provided based on such operation can be expressed as follows.

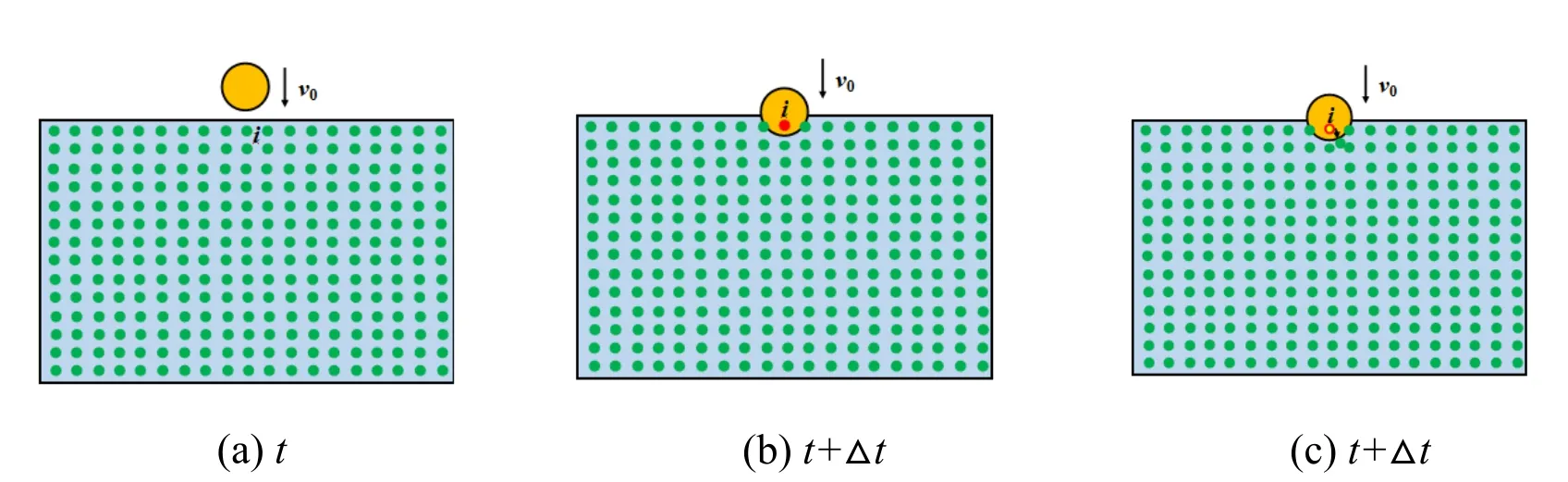
Figure 3:The material particles relocated inside the ice to display the collision with the rigid ball

At the time step(t+Δt),in a new location,we can get the velocity of such a particlexicalculated as follows [Madenci and Oterkus (2014)]:

We can get the total contact force as follows [Madenci and Oterkus (2014)],which exerts between the impact projectile and the stationary solid.

4.3 Adaptive particle refinement theory

To reproduce the physical phenomena in the ice impact problem applications,especially for the cases to simulate ice craters by impact,sufficient refinement particle resolution should be adopted.Conventional peridynamics simulations discretize the ice model to a large number of particles with a uniform distribution,which leads to prohibitive computational costs.In order to reduce costs of the CPU time and memory requirements,the dynamics adaptive refinement method was applied to the peridynamic model.In this paper,the adaptive particle refinement method was adopted in peridynamic simulation,inspired by the SPH method.An example of a plane problem is presented to illustrate the precision of the proposed adaptive particle refinement method.For the first time,the state-based peridynamics with adaptive particle refinement method extended to the 3D simulation of ice crater.

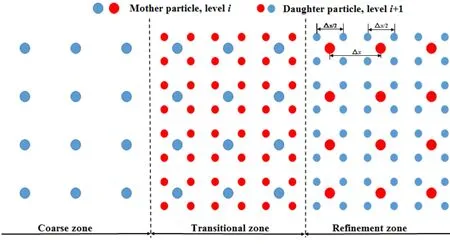
Figure 4:Sketch for the adaptive particle refinement (blue particle are active particle and red particles are inactive particle)

In the adaptive particle refinement method,the coarse particles should be refined (called mother particles) into fine particles (called daughter particles) in the main focus area [Sun,Zhang,Marrone et al.(2018)].As shown in Fig.4,a mother particle is defined into four daughter particles in 2D.Similarly in 3D,a mother particle will be defined into eight daughter particles.A parameter α is defined to determine the spacing between the daughter particle and the radius of the daughter particles corresponding to the mother particles as follows [López,Roose and Morfa (2013)]:

where the subscriptsmanddrepresent mother and daughter particles,respectively.In this paper,α= 0.5.The mass,momentum,and energy of the refinement process should conserve,as shown in Tab.1.

Table 1:Particle refinement conservation conditions

Because the particles in the horizon of each particle of the solid are fixed (which is different from the fluid particles),the coalescing process can be neglected in the PD adaptive refinement method.In the refinement zone,the mother particles will become inactive particles and are not considered for computing the governing equations.The physical variables can be obtained from the Shepard interpolation.On the contrary,the daughter particles in the refinement zone are active,and they will be involved in the calculation during the entire process.In the transition zone,the properties of the particles are the opposite of the refinement zone;the mother particles are active while the daughter particles are inactive particles.

To obtain the physical variables Ψi∈inactive[Bonet and Lok (1999)] of the inactive PD particles such as stress and velocity,we address the Shepard interpolation method as follows:

where N is the active particles’ total number including the horizon of the inactive particlei;andWijdenotes the influence function.According to the velocity obtained by interpolation,the position of the inactive particles can be updated by time integration.The inactive particle is also considered the damage criterion.If the stretch between two inactive particles is beyond the critical stretchs0,the bond existing at the two adjacent particles will be broken.After that,the inactive particle will no longer affect the active particle.

5 Numerical simulations

In the present work,the state-based peridynamic method was validated by using the numerical simulations to capture the ice crater problem.The simulation concludes the 2D and 3D models with adaptive particle refinement.The numerical results used in comparison with the experimental results validate the application of the proposed method.

5.1 Verification of the state-based peridynamics with adaptive particle refinement

To validate the objectivity of the proposed numerical algorithm,a quasi-static stretching of an elastic plate model was presented.A thin plate with the dimension of 0.01×0.01 m is considered,subjected to the traction of 20 m/s at the top and the bottom of the boundary,as shown in Fig.5(a).To check the sensitivity of the simulation results of the initial particle distributions,the uniform peridynamic simulations were compared to the adaptive particle refinement solutions.The whole domain of the uniform distribution contains 10,180 particles,and the grid size is 0.001 m.The refinement particles are 18,115,and the grid size in the refinement zone is 0.0005 m,as shown in Fig.5(b).Material parameters for ice are chosen as follows:the density ρ as 897.6 kg/m3,Poisson ratio ν as 0.33,and Young’s modulus E as 9.31 GPa.The time step is Δt=1.0×10-9s.

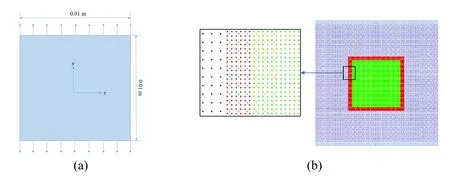
Figure 5:Illustration of a test plate model

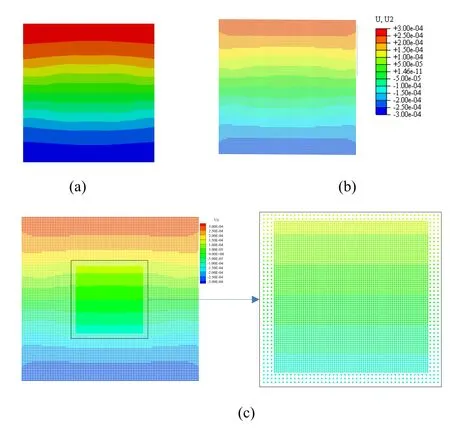
Figure 6:Comparison results of the Y displacement (a) FEM results (b) Peridynamics simulation with a uniform coarse grid (c) Peridynamics simulation with particle refinement grid

By comparing the FEM results and the simulation results in Fig.6,both the numerical results,uniform grid,and particle refinement grid coincide well with the FEM results,proving the availability of the implementation of the state-based peridynamic model.Another significant conclusion is that the particle refinement results coincide well with the uniform particle distribution,illustrating the precision of the proposed adaptive particle refinement technique.

5.2 Ice craters 2D simulation

In order to demonstrate the proposed numerical method to simulate the fragmentation of ice and understand the ice impact catering process,axial cylindrical symmetry is assumed for simplicity,and a 2D plane model was built.The ice target had a radius of 0.045 m and a depth of 0.08 m,and the projectile balls were modeled as spheres with diameterd=0.001 m.In Tab.2,the primary ice material parameters are listed.For simplicity,compared to the ice,the mass of the rigid projectile can be neglected,so that the projectile aimed to move at a constant speed as rigid.According to the compared experimental data [Shrine,Burchell and Grey (2002)],the projectile has different initial velocities,ranging from 1.07 to 7.04 km/s.

The mesh size for ice was chosen to be 0.0002 m.Therefore,we discretized the rigid ball into 48 hexahedral elements and 57 particles,and we discretized the ice target into 115,200 quadrilateral elements and 115,881 corresponding particles.The horizon δ is chosen to be three times the grid size.We set the boundaries to be free.The time step is Δt=5.0×10-9s.

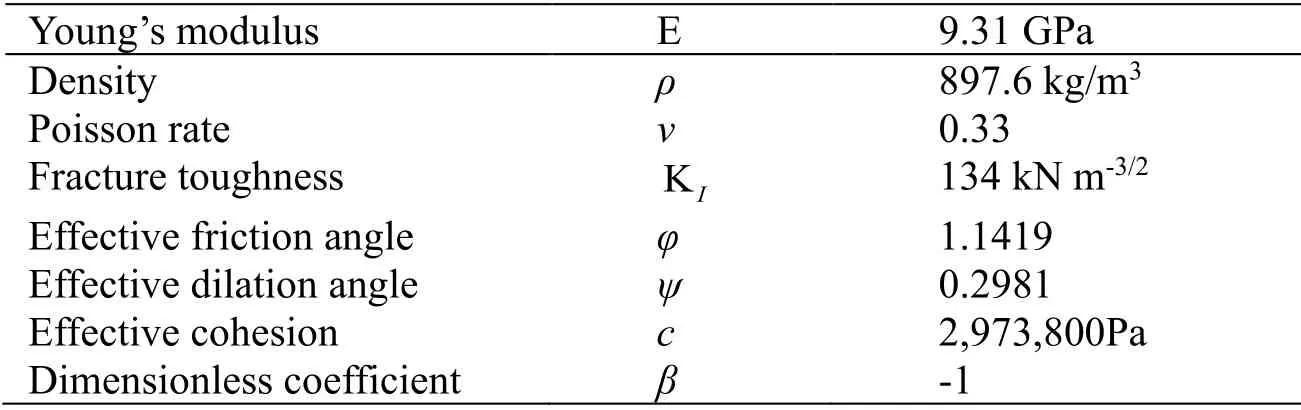
Table 2:Input parameters for ice material

A parametric study including analyzing the crater diameter,depth,and diameter ratio was carried out under the conditions of varies impact velocities.The definition of crater diameter D and depth H is shown in Fig.7.The simulation ran until the shape of the ice crater underwent no significant changes.The total time varied betweent= 1.0 × 1 0-9s andt=2.5 ×1 0-8s,depending on the initial velocity of the projectile.

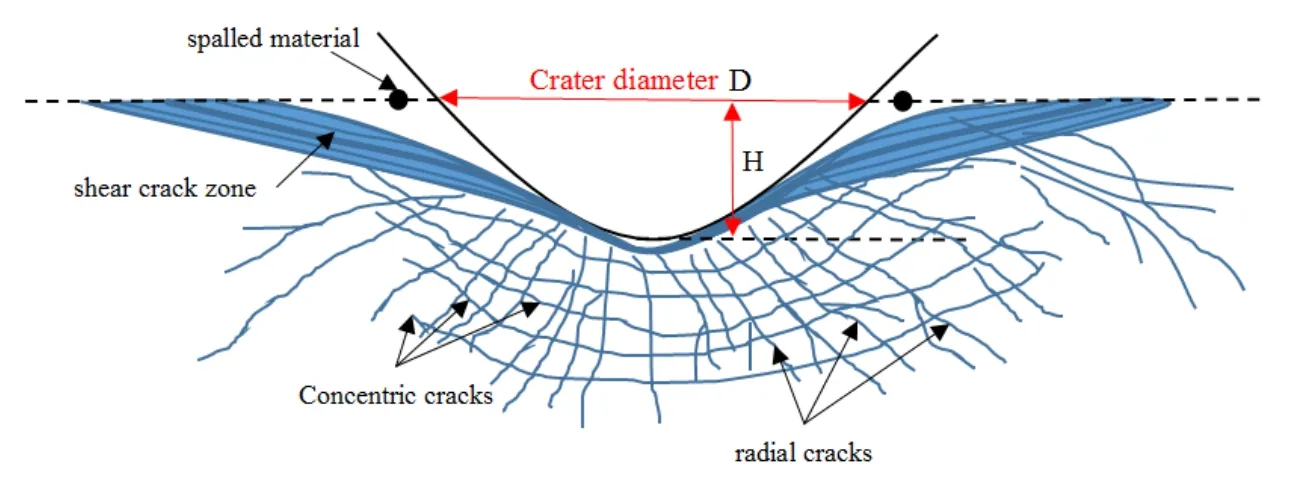
Figure 7:Definition of crater diameter D and crater depth H

From the simulation results,the first interesting observation is that the peridynamic model can observe the damage propagation of the ice target.The total plastic strain and the yield strength can be measured by damage.In general,the strength is assumed to be constant until the damage reached its critical value,then the cracks propagate freely through the ice target.If such cracks are near the surface,spall zone can be defined where the material would move and spall,as illustrated in Fig.7.Finally,the damage of the ice is defined as a scalar quantity in the peridynamic model that comprises shear crack zone,cracks,and spalled material,as shown in Fig.7.

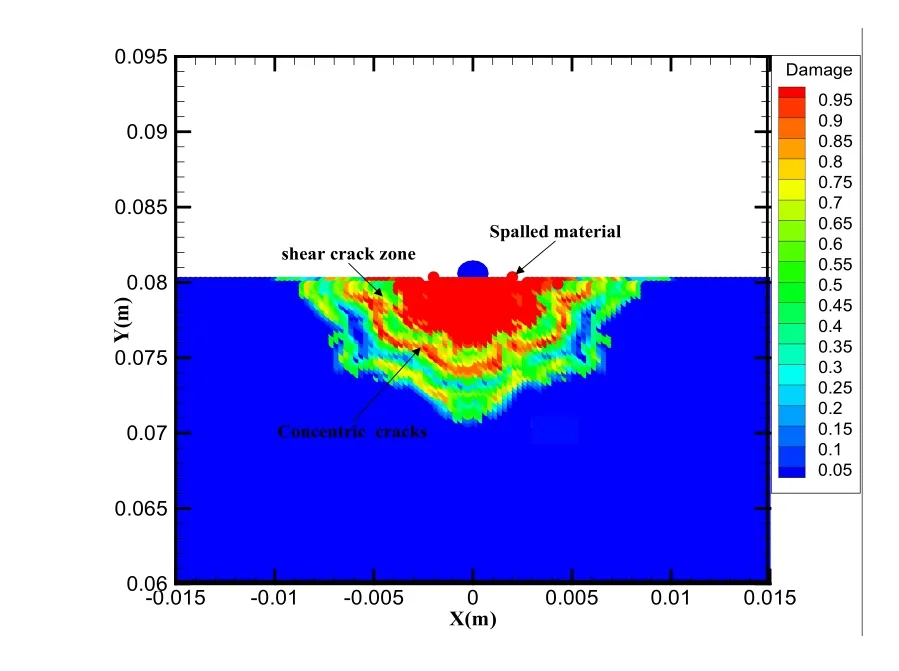
Figure 8:Damage contours plot with an impact velocity of 1.0 km/s

Fig.8 shows the simulation results of the damage contours under the impact condition of 1.0 km/s velocity.From Fig.8:(a) the damaged area is around 1 or 1.5x larger than the total ice cratering area (shown in red color),and the propagation of the damage directly affects the crater evolution;(b) the peridynamic simulation can capture the split material and concentric cracks defined in Fig.7.

Figure 9:Damage contours of ice at a different impact speed

The second important observation is the final forming shape of the ice craters.The peridynamic simulation damage contours of ice at different impact speeds are shown in Fig.9.Assuming that the crater depth and diameter were nearly identical,the projectile velocity is typically chosen to be 1.0,2.5,4.0,and 6.5 km/s.From Fig.9,the crater shape exhibited similar shapes for the cases of 1.0 and 2.5 km/s,which can be observed as concentric cracks and a small pit hole at the bottom of the ice crater.On the contrary,the final crater shape changed at projectile velocities over 4.0 km/s.The craters exhibited damaged cracks along the radial region,as shown in Figs.9(c) and 9(d).

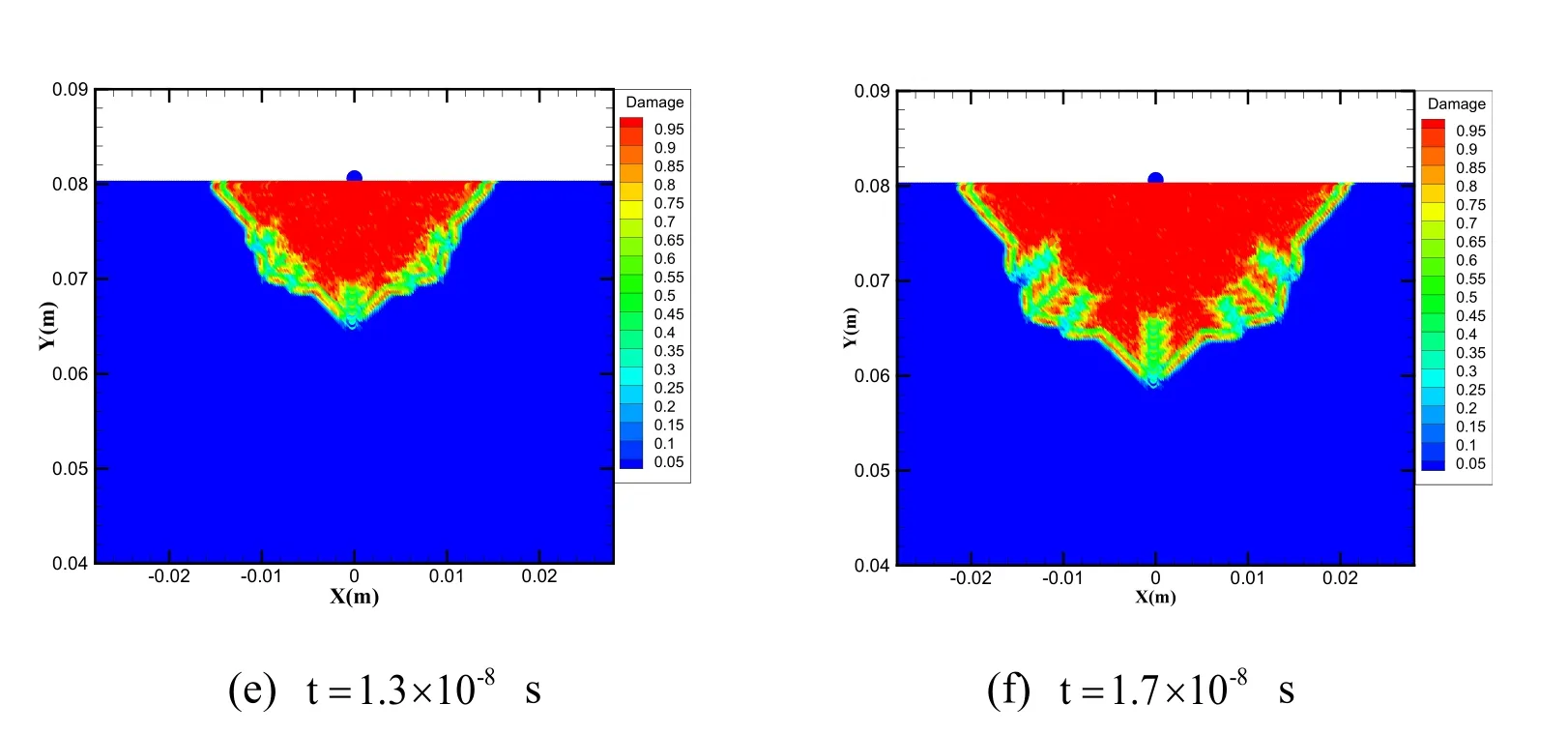
Figure 10:Damage propagation in ice under the projectile velocity of 4.0 km/s (a) Damage counters of the contact and contraction step t=5.0 ×10-9 s ;(b) End of contact and contraction step t= 8.0 ×1 0-9 s ;(c) Damage counters of the initial cracks progression step t=9.0 ×10-9 s ;(d) End of initial cracks progression step t=1.0 ×10-8 s ;(e) Damage counters of the ice craters shaping step t= 1.3 × 1 0-8 s ;(f) End of the ice craters shaping step t= 1.7 ×1 0-8 s

The last important issue to study is the damage propagation of ice cratering during the impact,which can be comprised into three general steps [Jesse (2010)]:(1) the contact and contraction step;(2) initial crack progression step;and (3) ice craters shaping step.Ice crater development at different steps can be observed in Fig.10.We define the first step to be the contact and the contraction step,the rigid projectile first come into the ice target and interact with the ice,as shown in Figs.10(a) and 10(b).This step begins with the impact loading from the rigid projectile.The second step is defined as the initial crack progression step,as shown in Figs.10(c) and 10(d).This step commences when the damage starts to accumulate,and cracks continue to grow and terminate when the crack diameter shows no significant growth.The damage progression step ends att= 1.0 ×1 0-8s.The third step is called the ice craters shaping step,as shown in Figs.10(e) and 10(f).The layer of 0.95 damaged ice began to expand rapidly along the cracks from the previous step as the ice was compressed and continued to grow horizontally along the crater until the final crater shape formulated.This step ended when the damaged ice stopped increasing.

5.3 Ice craters 3D simulation with adaptive particle refinement

Although the 2D simulation can capture most of the ice behavior features during the cratering process with less time and computational costs,it is still a challenging work to reproduce the physical phenomena,and sufficient refinement particle solution should be proposed.In the 3D simulations of the ice craters problem,the number of ice particles discretized in peridynamics is too large to use as a uniform particle distribution,which may lead to computational costs.In order to address this problem,an adaptive particle refinement solution is adopted.The adaptive particle refinement 3D model is shown in Fig.11.The ice target is a cylinder with a diameter of 0.09 m and 0.04 m high.The diameter of the projectile ball is 0.002 m.The ice was discretized into 1,113,364 peridynamic particles correspondingly.Material parameters for ice are similar to the previous model listed in Tab.2.The time step is Δt=1.0×10-9s.We set the boundaries to be free.The projectile velocities were chosen to be 1.0 km/s.

Figure 11:3D numerical model with adaptive particle refinement

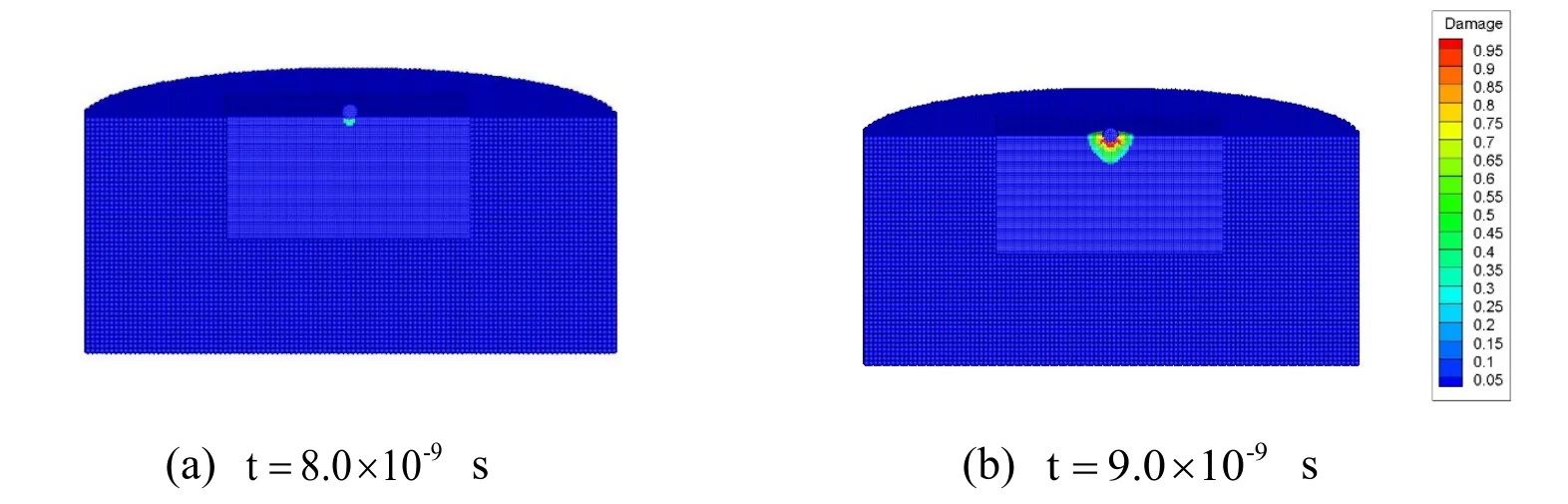
Figure 12:Different stages of damage contours of ice at a velocity of 1.0 km/s

Fig.12 shows the contours of the damage at different time stages under the condition of 1.0 km/s impact velocity.As damage accumulates,the energy wave quickly propagates through the refinement zone of the ice target,which indicates that the state-based peridynamic model with adaptive particle refinement technique is successful.

5.4 Analysis and discussion

Comparing the peridynamic simulation results with the previous experimental data (as shown in Figs.13-15),it can be found that the diameter obtained from the numerical simulations is in good agreement with previous experimental data.

Figure 13:Crater depth vs. velocity

The influence of the projectile velocity on the crater depths is shown in Fig.13.The peridynamic simulation follows the power law trend and coincides well with the power law function.The simulation results were mildly above the experimental data but were well within the indeterminacy of the power law function.The equation of the power law correlation is as follows [Shrine (2002)]:

where H is the crater depth in mm;Vis the impact velocity in km/s;and R2is the correlation coefficient.

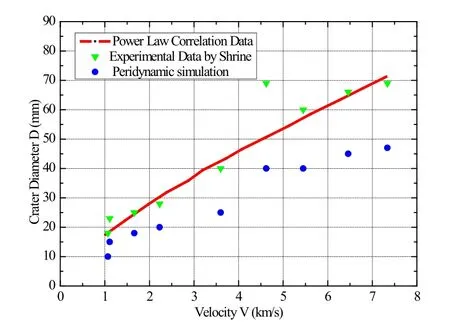
Figure 14:Crater diameter vs. impact velocity

The relationship between the velocity of the projectile and the crater diameter is shown in Fig.14.Compared with the peridynamic simulation.Shrine et al.[Shrine,Burchell and Grey (2002)] developed the experimental data according to the power law fit as follows:

where D is the crater diameter;and V is the projectile velocity.

From Fig.14,the peridynamic simulation data were smaller than the experimental data.However,all of the peridynamic simulation results were within the same increasing trend of the power law denoted by Eq.(72).

Figure 15:Spall diameter ratio vs. impact velocity

Fig.15 shows the influence of the velocity on the spall diameter ratio (H/D),which was plotted by the comparison of the experimental data.The power law is given in Eq.(73) [Shrine,Burchell and Grey (2002)]:

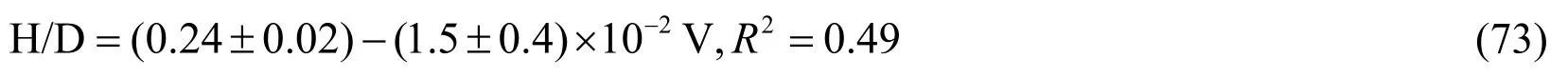
It can be observed that the peridynamic simulation performs on a similar trend to the experimental data,which is approximately a small decrease from 0.3 at 1 km/s to just below 0.2 at 7 km/s.Fig.15 shows that with the increase of the velocity,the crater depth to crater diameter ratio gradually decreased.

From the comparison,it can be validated that the state-based peridynamics can simulate the general characteristics of ice crater by impact.Although the model can exceptionally capture ice crater depth,not all of the ice crater diameters can be obtained due to the initial imperfection of the material and the energy dissipation during the ice cratering process.The advantage of using the peridynamic simulation is that the peridynamics can simulate the evolution of the ice cratering procedure,which is limited during experimental tests.The experiments conducted by Shrine et al.[Shrine,Burchell and Grey (2002)] can only measure the physical features of the ice crater after the impact.

6 Conclusions

In this paper,a modified Drucker-Prager constitutive model for ice based on stated-based Peridynamics with adaptive particle refinement technique is developed to simulate the impact cratering in ice.The critical advantage in this study is that the constitutive ice model was implemented into the peridynamic equations.The proposed numerical model can be divided into two parts:elastic-plastic deformation,and brittle failure.The modified Drucker-Prager peridynamic model was adopted to analyze the elastic-plastic deformation,and we use the fracture toughness failure criterion of ice in peridynamics to simulate the brittle process.The proposed state-based peridynamic method was validated by the numerical simulations.Comparing with the previous experimental data from the open literature,the numerical results coincided well with the previous studies (not only from the view of the parametric study but also from the view of damage propagation of ice).Another important advantage is that the state-based peridynamics with adaptive particle refinement technique is extended to the 3D simulation of ice crater for the first time.The adaptive particle refinement technique can save the CPU time and memory requirements caused by a large number of particles with a uniform distribution and a constant horizon in conventional peridynamic simulations.The last significant result is that this validation process develops the dynamic characteristic of the ice.It can be illustrated that the state-based peridynamic model is capable of representing ice craters features.Considering the high strain rate and temperature effect of the ice,an improved peridynamic model with transient heat conduction and thermomechanical deformation in ice will be presented in the future.

Acknowledgment:The author gratefully acknowledges the financial support from the Chinese Scholar Council (CSC No.201706680094) and the University of California Berkeley.The authors greatly appreciate Prof.Xiaoying Zhuang from Leibniz University Hannover for her guidance.The authors thank reviewers for their valuable comments and suggestions.

References

Barcarolo,D.A.;Le Touzé,D.;Oger,G.;De Vuyst,F.(2014):Adaptive particle refinement and derefinement applied to the smoothed particle hydrodynamics method.Computational Physics,no.273,pp.640-657.

Bergel,G.L.;Li,S.(2016):The total and updated lagrangian formulations of state-based peridynamics.Computational Mechanics,vol.58,no.2,pp.351-370.

Bobaru,F.;Ha,Y.D.(2011):Adaptive refinement and multiscale in 2D peridynamics.Multiscale Computational Engineering,vol.9,no.6,pp.635-659.

Bonet,J.;Lok,T.S.(1999):Variational and momentum preservation aspects of smooth particle hydrodynamic formulations.Computer Methods in Applied Mechanics and Engineering,vol.180,no.1-2,pp.97-11.

Cui,P.;Zhang,A.M.;Wang,S.;Khoo,B.C.(2018):Ice breaking by a collapsing bubble.Fluid Mechanics,vol.841,pp.287-309.

Dipasquale,D.;Zaccariotto,M.;Galvanetto,U.(2014):Crack propagation with adaptive grid refinement in 2D peridynamics.Fracture,vol.190,pp.1-22.

Drucker,D.C.;Prager,W.(1952):Soil mechanics and plastic analysis or limit design.Quarterly of Applied Mathematics,vol.10,pp.157-165.

Fan,H.;Bergel,G.L.;Li,S.(2016):A hybrid peridynamics-SPH simulation of soil fragmentation by blast loads of buried explosive.Impact Engineering,vol.87,pp.14-27.

Fan,H.;Li,S.(2017):A Peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads.Computer Methods in Applied Mechanics and Engineering,vol.318,pp.349-381.

Fan,H.;Li,S.(2017):Parallel peridynamics-SPH simulation of explosion induced soil fragmentation by using OpenMP.Computational Particle Mechanics,vol.4,no.2,pp.199-211.

Fan,H.;Ren,B.;Li,S.(2015):An adhesive contact mechanics formulation based on atomistically induced surface traction.Computational Physics,vol.302,pp.420-438.

Gao,Y.;Hu,Z.;Ringsberg,J.W.;Wang,J.(2015):An elastic-plastic ice material model for ship-iceberg collision simulations.Ocean Engineering,vol.102,pp.27-39.

Gao,Y.;Hu,Z.;Wang,J.(2014):Sensitivity analysis for iceberg geometry shape in ship-iceberg collision in view of different material models.Mathematical Problems in Engineering,vol.2014,pp.1-11.

Ha,Y.D.;Bobaru,F.(2011):Characteristics of dynamic brittle fracture captured with peridynamics.Engineering Fracture Mechanics,vol.78,no.6,pp.1156-1168.

Hanninen,S.(2005):Incidents and Accidents in Winter Navigation in the Baltic Sea,Winter 2002-2003.Finnish Maritime Administration.

Hughes,T.J.;Winget,J.(1980):Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis.Numerical Methods in Engineering,vol.15,no.12,pp.1862-1867.

Lai,X.;Liu,L.;Li,S.;Zelekea,M.;Liu,Q.et al.(2018):A non-ordinary state-based peridynamics modeling of fractures in quasi-brittle materials.Impact Engineering,vol.111,pp.130-146.

Lange,M.A.;Ahrens,T.J.(1981):Fragmentation of ice by low velocity impact.Proceedings of the 12th Lunar and Planetary Science Conference,vol.2,pp.1667-1687.

Li,S.;Hao,W.;Liu,W.K.(2000):Numerical simulations of large deformation of thin shell structures using meshfree methods.Computational Mechanics,vol.25,pp.102-116.

Li,S.;Qian,D.;Liu,W.K.;Belytschko,T.(2001):A meshfree contact-detection algorithm.Computer Methods in Applied Mechanics and Engineering,vol.190,pp.3271-3292.

Liu,G.R.;Liu,M.B.(2003):Smoothed Particle Hydrodynamics:A Meshfree Particle Method.Singapore:World Scientific.

Liu,H.W.;Miller,K.J.(1979):Fracture toughness of fresh-water ice.Glaciology,vol.22,no.86,pp.135-143.

Liu,M.H.;Wang,Q.;Lu,W.(2017):Peridynamic simulation of brittle-ice crushed by a vertical structure.Naval Architecture and Ocean Engineering,vol.9,no.2,pp.209-218.

Liu,R.W.;Xue,Y.Z.;Lu,X.K.;Cheng,W.X.(2014):Simulation of ship navigation in ice rubble based on peridynamics.Ocean Engineering,vol.148,pp.286-298.

Liu,Z.;Amdahl,J.;Løset,S.(2011):Plasticity based material modelling of ice and its application to ship-iceberg impacts.Cold Regions Science and Technology,vol.65,no.3,pp.326-334.

López,Y.;Roose,D.;Morfa,C.R.(2013):Dynamic particle refinement in SPH:application to free surface flow and non-cohesive soil simulations.Computational Mechanics,vol.51,no.5,pp.731-741.

Madenci,E.;Oterkus,E.(2014):Peridynamic Theory and Its Applications,pp.125-150.Springer,New York.

Peng,Y.X.;Zhang,A.M.;Ming,F.R.(2018):A thick shell model based on reproducing kernel particle method and its application in geometrically nonlinear analysis.Computational Mechanics,vol.62,no.3,pp.309-321.

Pernas-Sánchez,J.;Pedroche,D.A.;Varas,D.;López-Puente,J.;Zaera,R.(2012):Numerical modeling of ice behavior under high velocity impacts.Solids and Structures,vol.49,no.14,pp.1919-1927.

Poelchau,M.H.;Kenkmann,T.;Hoerth,T.;Schäfer,F.;Rudolf,M.et al.(2014):Impact cratering experiments into quartzite,sandstone and tuff:the effects of projectile size and target properties on spallation.Icarus,vol.242,no.2,pp.11-24.

Rabczuk,T.;Ren,H.;Zhuang,X.(2019):A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem.Computers,Materials &Continua,vol.59,no.1,pp.31-55.

Ren,B.;Li,S.(2010):Meshfree simulations of plugging failures in high-speed impacts.Computers &Structures,vol.88,pp.909-923.

Ren,B.;Li,S.;Qian,J.;Zeng,X.(2011):Meshfree simulations of spall fracture.Computer Methods in Applied Mechanics and Engineering,vol.200,pp.797-811.

Ren,H.;Zhuang,X.;Cai,Y.;Rabczuk,T.(2016):Dual-horizon peridynamics.Numerical Methods in Engineering,vol.108,no.12,pp.1451-1476.

Ren,H.;Zhuang,X.;Rabczuk,T.(2017):Dual-horizon peridynamics:a stable solution to varying horizons.Computer Methods in Applied Mechanics and Engineering,vol.318,pp.762-782.

Ren,H.;Zhuang,X.;Rabczuk,T.(2018):Dual-support smoothed particle hydrodynamics in solid:variational principle and implicit formulation.arXiv:1810.06010.

Rist,M.A.(1997):High-stress ice fracture and friction.Physical Chemistry B,vol.101,no.32,pp.6263-6266.

Schulson,E.M.(2001):Brittle failure of ice.Engineering Fracture Mechanics,vol.68,no.17-18,pp.1839-1887.

Selvadurai,A.P.S.(2009):Fragmentation of ice sheets during impact.Computer Modeling in Engineering &Sciences,vol.52,no.3,pp.259-277.

Sherburn,J.A.;Horstemeyer,M.F.(2010):Hydrodynamic modeling of impact craters in ice.Impact Engineering,vol.37,pp.27-36.

Shrine,N.R.;Burchell,M.J.;Grey,I.D.(2002):Velocity scaling of impact craters in water ice over the range 1-7.3.Icarus,vol.155,no.2,pp.475-485.

Silling,S.A.;Askari,E.(2005):A meshfree method based on the peridynamic model of solid mechanics.Computers &Structures,vol.83,no.17,pp.1526-1535.

Silling,S.A.;Epton,M.;Weckner,O.;Xu,J.;Askari,E.(2007):Peridynamic states and constitutive modeling.Elasticity,vol.88,no.2,pp.151-184.

Song,Y.;Yu,H.;Kang,Z.(2018):Numerical study on ice fragmentation by impact based on non-ordinary state-based peridynamics.Micromechanics and Molecular Physics,vol.4,no.1,1850006.

Sun,P.;Zhang,A.M.;Marrone,S.;Ming,F.(2018):An accurate and efficient SPH modeling of the water entry of circular cylinders.Applied Ocean Research,vol.72,pp.60-75.

Wang,G.;Ji,S.H.(2006):Drucker-Prager yield criteria in viscoelastic-plastic constitutive model for sea ice dynamics.Engineering Mechanics.vol.23,no.6,pp.154-163.

Wang,P.;Zhang,A.M.;Ming,F.;Sun,P.;Cheng,H.(2019):A novel non-reflecting boundary condition for fluid dynamics solved by smoothed particle hydrodynamics.Fluid Mechanics,vol.860,pp.81-114.

Wang,Q.;Wang,Y.;Zan,Y.F.;Lu,W.;Bai,X.L.et al.(2018):Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion.Marine Science and Technology,vol.23,no.1,pp.52-66.

Ye,L.Y.;Wang,C.;Chang,X.;Zhang,H.Y.(2017):Propeller-ice contact modeling with peridynamics.Ocean Engineering,vol.139,pp.54-64.

Zhang,A.M.;Sun,P.N.;Ming,F.R.;Colagrossi,A.(2017):Smoothed particle hydrodynamics and its applications in fluid-structure interactions.Hydrodynamics,vol.29,no.2,pp.187-216.