A Possible Reason About Origin of Singularity and Anomalous Dispersion in Peridynamics

Xinfeng Wang and Zaixing Huang

1State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,China.

Abstract:In the benchmark problems of peridynamics,there are some eccentric results,for example,singularity of uniaxial tension and anomalous dispersion of wave.The reasons to give rise to these results are investigated.We calculated local tension and wave of an infinite rod after adding a divergence of local stress in the peridynamic motion equation.The acquired results verify that the singularity in the peridynamic solution of local tension problem and anomalous dispersion of peridynamic wave are all eliminated.Therefore,the anomalous features of some peridynamic solutions likely stem from the lack of local stress characterizing contact interactions.

Keywords:Peridynamics,singularity of displacement,anomalous dispersion,peridynamic wave.

1 Introduction

Peridynamics [Silling (2000);Silling and Lehoucq (2010)] is a new branch of continuum mechanics developed at recent two decades.Its motivation is to relax the requirement of continuity for the displacement field so as to conveniently analyze deformation companied with evolution of discontinuities caused by damage,fracture and impact breakage [Silling and Lehoucq (2010);Madenci and Oterkus (2014);Bobaru,Foster,Geubelle et al.(2017)].Based on this motivation,strain and stress are kicked out from peridynamics.They are replaced by relative displacement and internal long-range body force associated with the relative displacement,respectively.However,any profit always accompanies loss.Then,what is the cost of abandoning the strain and stress? This problem has been partially investigated by Weckner et al.[Weckner,Brunk,Epton et al.(2009)] and Wang et al.[Wang,Xu and Wang (2017)].They solved the Green functions of peridynamics,and compared singularities in the Green functions of peridynamics and classical elasticity.In order to further clarify this question,we compare peridynamics with physically-based nonlocal elasticity [Di Paola,Failla and Zingales (2009);Di Paola,Pirrotta and Zingales (2010)] through two benchmark examples.Different from the classical elasticity and peridynamics,the physically-based nonlocal elasticity contains both local stresses and long-range interactin forces,while the classical elasticity only involves the local stresses,and peridynamics only concerns the long-range interactin forces.

In peridynamics,most of problems are solved based on numerical algorithm.So far,only a few analytical solutions are acquired for some simple benchmark problems such as uniaxial tension and longitudinal vibration of rod.Silling et al.[Silling,Zimmermann and Abeyaratne (2003)] analyzed the deformation of an infinite rod subjected a simplepoint load and gave a divergent form solution.Weckner et al.[Weckner and Abeyaratne(2005);Weckner,Brunk and Epton et al.(2009)] found the Green’s functions of 1-and 3-dimensional peridynamics with help of the Laplace and Fourier transforms.By these Green’s functions,they gave an integral representation of 3-dimensional peridynamic solution.Using the similar approach,Mikata [Mikata (2012)] investigated the peristatic and peridynamic analytical solutions of a 1-dimensional infinite rod.These solutions are represented as the sum of the Dirac delta functions and a convergent integral.Further,Wang et al.[Wang,Xu and Wang (2017)] proved that the Green’s functions are uniformly expressed as conventional solutions plus Dirac functions,and convergent nonlocal integrals.Huang[Huang (2017)]solved the local uniaxial tension based on nonordinary state-based peridynamics.

Recently,Bazant and his colleagues discussed improvable physical aspects of peridynamics through analyzing the dispersion of wave [Bazant,Luo and Chau et al.(2016)].As a response,Butt,Timothy and Meschke proposed that the strong dispersion of peridynamic wave can be minimized by choosing a combination of the size of the peridynamic horizon and the shape of the influence function in a way that the peridynamic solution approaches the solution of classical elasticity[Butt,Timothy and Meschke (2017)].

The peridynamic solutions mentioned above all contain a singular Dirac delta function or anomalous dispersion.Where do these singularity or anomalous dispersion come from?Are they caused by peridynamic motion/equilibrium equation or constitutive equation? To answer these questions,peridynamic motion equation and relevant constitutive equations were investigated once again.We found that some eccentric results in peridynamics may be caused by the lack of local stress to a considerable degree.

The outline of the paper is as follows.In Section 2,we discuss internal interactions in peridynamic medium.The 1-dimensional motion equations of peridynamic and the physically-based nonlocal elasticity are compared in Section 3.Their difference and correlation are discussed.In Section 4,we solve the local uniaxial tension of an infinite rod based on peridynamics and the physically-based nonlocal elasticity,respectively.The analytical solutions are acquired,and their characteristics are compered and analyzed.The dispersions of two kind of waves are investigated in Section 4.The dispersion curves corresponding to different micro-modulus and nonlocal kernel are discussed in detail.Finally,we close this paper with summary and comment.

2 Internal interactions in peridynamics

Let Ω denote spatial domain occupied by a body.Hx(Hx ⊂Ω)is a peridynamic family at point x(x∈Ω),as shown in Fig.1.In peridynamics,the motion equation of the body is written as[Silling (2000);Silling and Lehoucq (2010)]

where f(x,x′,t)is peridynamic force characterizing long-range interactions within body,b(x,t)is external body force,ρ(x)is mass density and u(x,t)the displacement field.The peridynamic force complies with the antisymmetric relation below

Integrating Eq.(1)onHx,we have

It can be also rewritten as[Silling and Lehoucq (2010)]

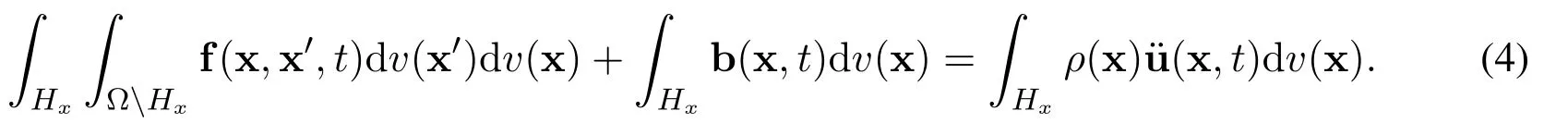
Eq.(4)is valid for bond-based and state-based peridynamics.The first term of it represents the long-range interactions betweenHxand ΩHx.Clearly,there is no term describing the contact interactions on the interface∂Hxin Eq.(4).

Figure 1:Peridynamic family Hx(Hx ⊂Ω)at point x(x ∈Ω)

To clarify origin of this point,let us observe physically-based nonlocal elasticity (PNE),whose master equation reads[Di Paola,Failla and Zingales (2009);Di Paola,Pirrotta and Zingales (2010);Huang (2012)]

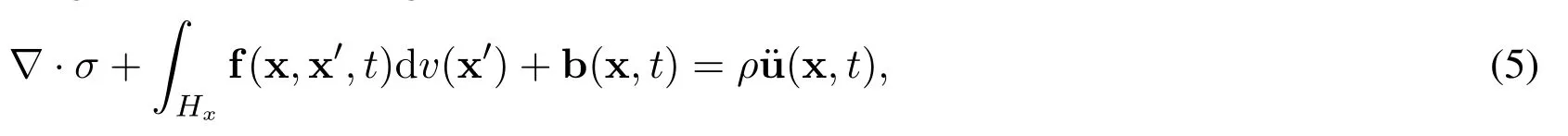
in which f(x,x′,t)is still subjected to the constraint of Eq.(2).Integrating Eq.(5)onHxleads to

where p(x,t) =σ ·n,being traction on interface betweenHxand Ω/Hx.This traction characterizes the contact forces applied onHxby Ω/Hx.Therefore,we see that peridynamics lacks a local stress describing contact interactions.Is the lack of local stress the cause of the singularity and anomalous dispersion of peridynamic solutions.Next we turn to discussing this question.

3 Basic equations of physically-based nonlocal elasticity and peridynamics

In order to understand the origin of singularity and anomalous dispersion in the peridynamic solutions,let us use,respectively,physically-based nonlocal elasticity and peridynamics to calculate local tension and wave of an infinite rod.Consider an infinite 1-dimensional homogeneous medium.The governing equation of physically-based nonlocal elasticity can be written as [Di Paola,Failla and Zingales (2009);Di Paola,Pirrotta and Zingales (2010);Huang (2012)]

whereβis a normalized parameter,u(x,t) denotes the displacement,b(x,t) is the prescribed load,ρandEare the line mass density and elastic modulus,andK(x′-x,τ)is referred to as the nonlocal kernel in whichτis a scale parameter.Whenτ →0,the value ofβis required to ensure that Eq.(7)can degrade into the classical elastodynamic equation.On the other hand,the governing equation of peridynamics has the form below [Silling(2000);Silling and Lehoucq (2010)]

whereC(x′ - x,l) is the so-called micro-modulus andlis also a scale parameter.In general,K(x′-x,τ)/=C(x′-x,l),but they are all of symmetry[Silling (2000);Silling and Lehoucq (2010)],i.e.,K(x′-x,τ)=K(x-x′,τ)andC(x′-x,l)=C(x-x′,l).

Eq.(7) is independent of Eq.(8).However,under some special conditions,they can be also correlated to each other.For example,Eq.(7)can be transformed into Eq.(8)through the equality below

whereδ(ξ) is the Dirac delta function.In the same way,Eq.(8) can be also acquired by Eq.(7).

Whenτ →0 andl →0,Eqs.(7) and (8) should return to the governing equation of classical elastodynamics.As a result,it is necessary that the following equalities hold,i.e.,

For simplicity,we setγ=β.This equality combining withβ+γ= 1 leads toβ=γ=1/2.Comparing Eq.(10)with Eq.(11),we further have

Using Eqs.(7) and (8),in the following we will firstly calculate the local tension of an infinite rod.

4 Local uniaxial tension in an infinite rod

4.1 The formal solutions

The local uniaxial tension of infinite rod is defined as the tension of a finite segment between two points in the infinite rod,as shown in Fig.2.

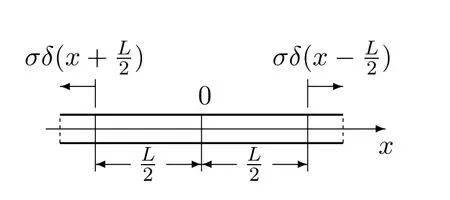
Figure 2:Local uniaxial tension of an infinite rod

When we calculate the local uniaxial tension,the inertia effect can be ignored.By Eq.(12),so Eqs.(7)and(8)are simplified into

where

For the convenience of distinction,we have useduNanduPto replaceuin Eqs.(13) and (14),respectively.Applying the Fourier transform (it is defined as ˆf(k) =to Eqs.(13)and(14),we have(see Appendix A)

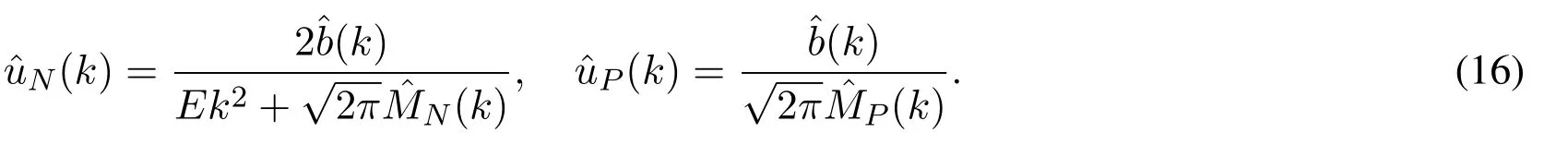
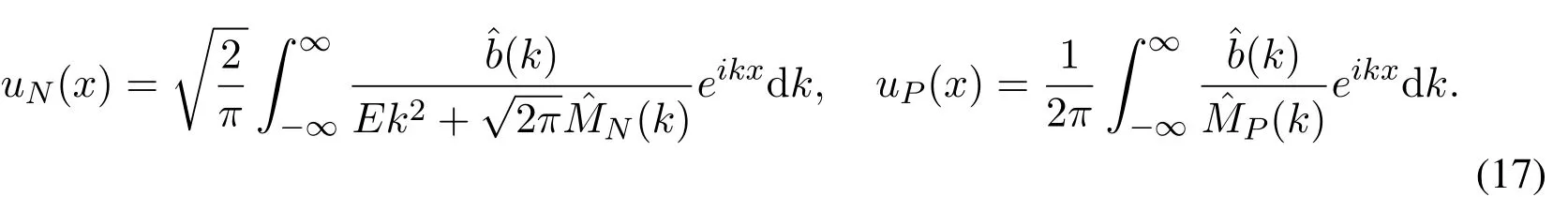
As shown in Fig.1,the total load applied on the rod can be written as

whose Fourier transform reads

Example 1:

Example 2:

It is easy to verify that Eqs.(20)and(21)satisfy the limitation given by Eq.(11).Taking the Fourier transform of Eqs.(20)and(21),we have

Substituting Eqs.(19),(22)and(23)into(17),we acquire the formal solutions below.

PNE solutions:

Peridynamic solutions Mikata (2012):

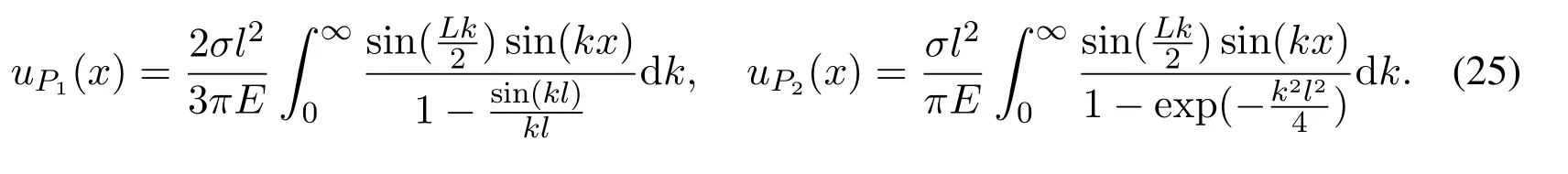
Figure 3:Distribution of displacement along the bar in Example 1 when σ/E = 1 and L=1(l=1.2:black doted line;l=0.8:blue dot-dashed line;l=0.2:green dashed line;l=0:red solid line)

4.2 Analysis and discussion

The formal solutions of peridynamics given by Eq.(25)were firstly treated by Silling et al.[Silling,Zimmermann and Abeyaratne (2003)]and[Mikata Mikata (2012)],respectively.Unfortunately,they are divergent.These divergent formal solutions can be transformed into a singular function plus a convergent integral [Mikata (2012);Wang,Xu and Wang(2017)].With the decrease ofl/L,the convergent integral will approach the elasto-static solution of local uniaxial tension(see Appendix B)

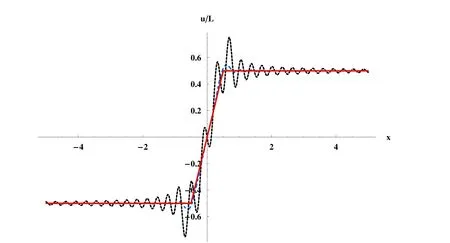
Figure 4:Distribution of displacement along the bar in Example 2 when σ/E = 1 and L=1(l=0.8:black doted line;l=0.5:blue dot-dashed line;l=0.1:green dashed line;l=0:red solid line)

On the other hand,inspecting Eq.(24)carefully,we have

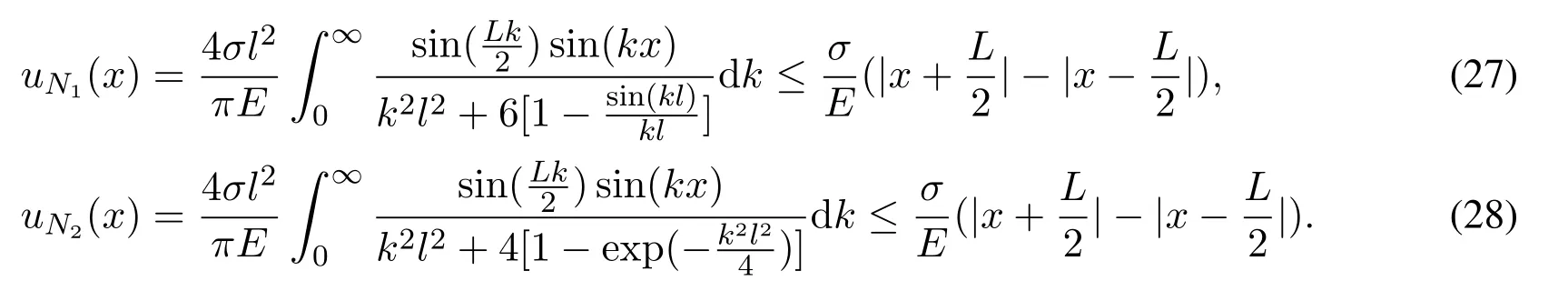
Therefore,the PNE solutionsuN1(x)anduN2(x)are convergent.By Eq.(24),we have

Just as mentioned in Section 3,whenl →0,uN1(x)anduN2(x)degrade to the classical elastostatic solution represented by Eq.(26).

Eq.(5) is acquired by taking a combination of the local stress divergence and Eq.(4).So the difference between the solution (24) and (25) comes from this divergence of local stress.Owing to introduction of this local stress,the singularity disappears in the solution of local tension.Therefore,we judge that the singularities of peridynamic solutions are likely caused by the lack of local stress,although this conclusion needs further verification.Figs.3 and 4 illustrate the similarity and difference between the nonlocal solutions and the elasto-static solution for the local uniaxial tension of infinite rod.From them,we see that the displacement distribution given by nonlocal solutions approaches the displacement field of the classical elasticity with the decrease of the scale parameterl.

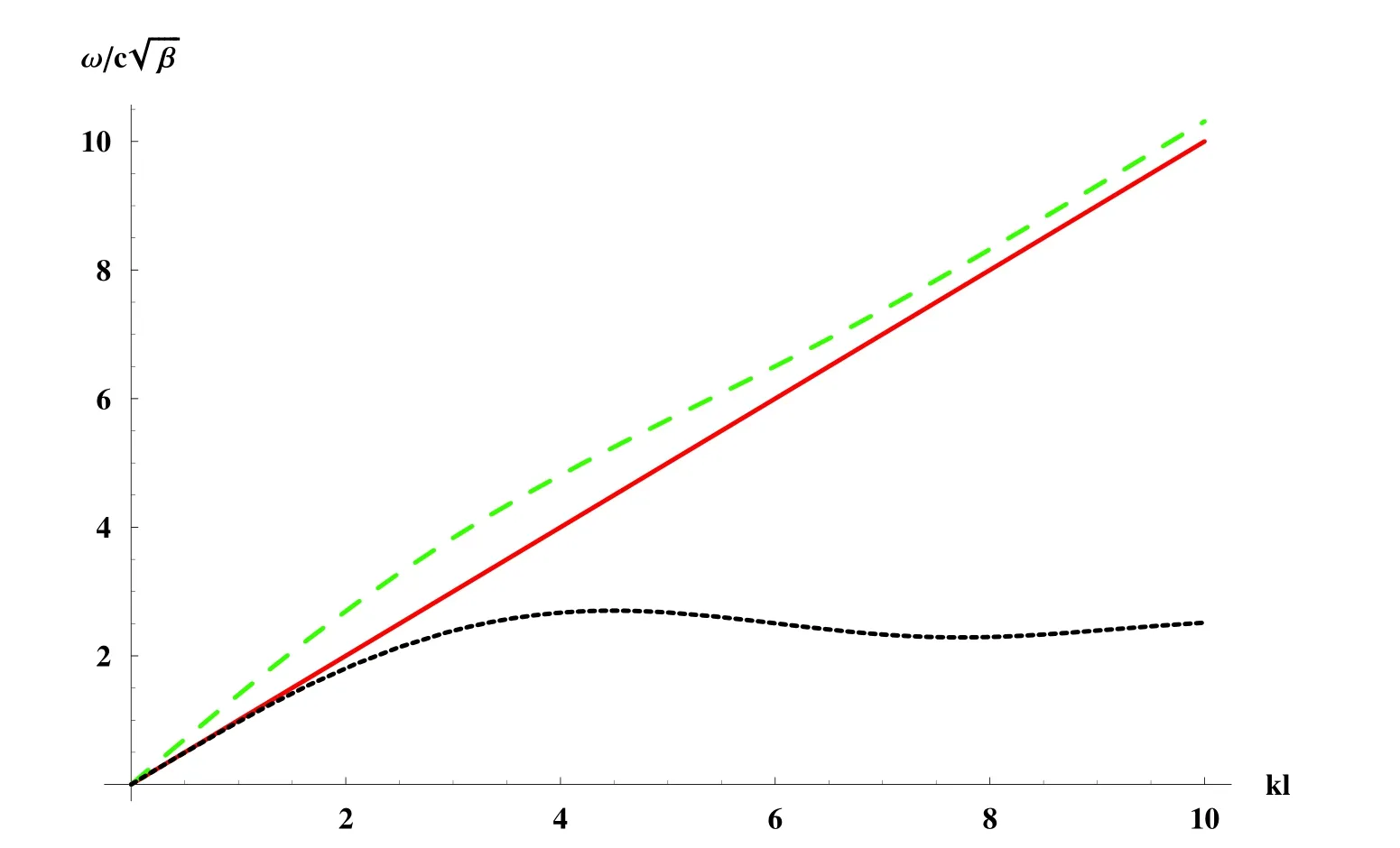
Figure 5:Dispersion curves of waves in Example 1(peridynamic:black doted line;PNE:green dashed line;elastic:red solid line)

5 Dispersion of wave

In order to compare the dispersion relation of physically-based nonlocal elastic wave and peridynamic wave,take the Laplace transform(i.e.,wheresis a complex number.) of Eqs.(7)and(8).As a result,we have

Not concerned with external stimuli and initial conditions,Eqs.(31)and(32)reduce to

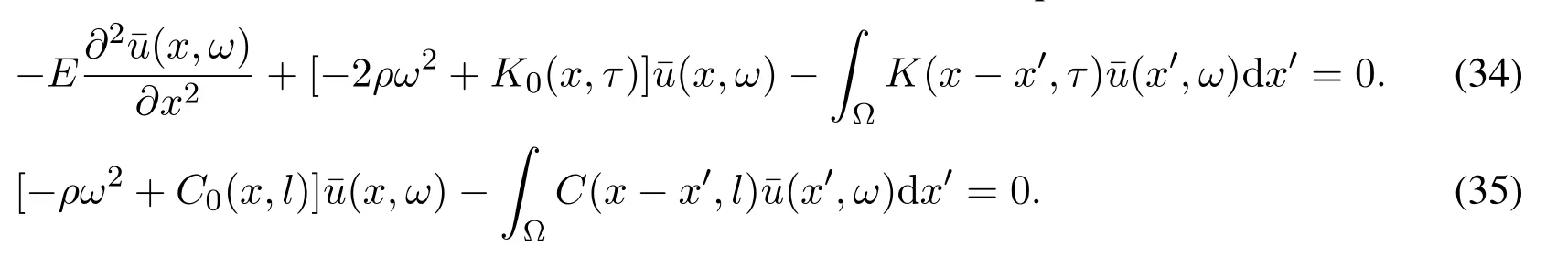
where we have sets=-iω.Applying the Fourier transform to Eqs.(34) and (35),we have

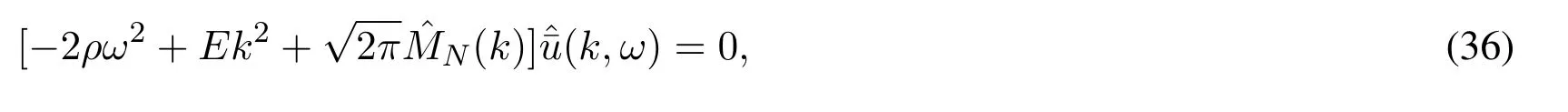
whereωandkrepresent the angular frequency and wave number,respectively.In general,(k,ω)/=0.So Eqs.(36)and(37)hold if and only if

Eqs.(38) and (39) are the dispersion relation of PNE wave and peridynamic wave,respectively.Substituting Eqs.(22) and (23) into (38) leads to the nonlocal dispersion relations below

Here,c=denotes the elastic wave speed.In the same way,the peridynamic dispersion relations can be given as follows

The dispersion curves determined by Eqs.(40)and(42)together with elastodynamics are depicted in Fig.5.We see that PNE wave and peridynamics wave always give rise to the dispersion,while the wave propagation has no dispersion in the classical elastodynamics.With the increase of angular frequency,the dispersion curve of PNE wave approaches the result of elastodynamics.It shows that the dispersion caused by nonlocality decays with the angular frequency increasing.

Fig.5 shows that there exists a maximum of angular frequency in the dispersion curve of the peridynamic wave.This is a result worth notice.It means that the propagation of wave is prohibited when the angular frequency exceeds this maximum.Meanwhile,the occurrence of negative slope in the dispersion curve shows that the group velocity of the peridynamic wave is negative.To the best of my knowledge,this is an anomalous dispersion,which has been pointed out by Bazant et al.[Bazant,Luo and Chau et al.(2016)],but not being observed in elastic wave.

Fig.6 shows that the peridynamic wave characterized by Eq.(21)is slightly different from that described by(20)in dispersion.The former has no the negative group velocity,but its angular frequency asymptotically approaches a constantwithk →∞.It implies that there is no wave that angular frequency is greater thanif Eq.(21)is used to characterize the constitutive behaviors of materials.By comparison of Fig.6 with Fig.5,it is easy to find that the dispersion of wave depends on the selection to the mathematical form of micro-modulus.

Compared peridynamics with physically-based nonlocal elasticity in dispersion curves,we see that peridynamic wave has an anomalous dispersion.As same as the singularity of peridynamic solution in the uniaxial tension,maybe this anomalous dispersion stems form the the lack of local stress characterizing the contact interaction.

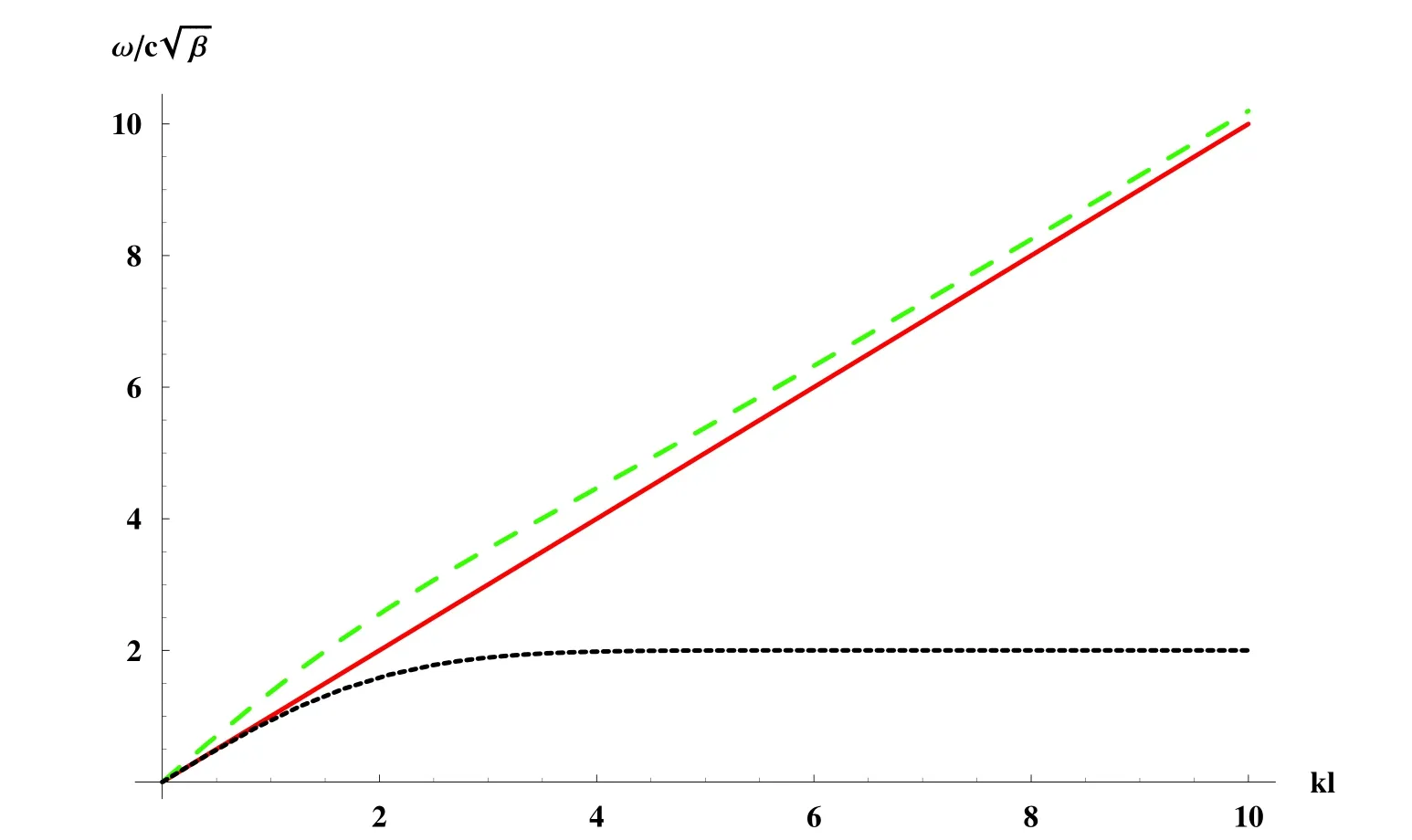
Figure 6:Dispersion curves of waves in Example 2(peridynamic:black doted line;PNE:green dashed line;elastic:red solid line)

6 Conclusions

Peridynamics and physically-based nonlocal elasticity are two kinds of nonlocal formulations with an inherent connection.Peridynamics abandons the local stress characterizing the contact interaction,while the physically-based nonlocal elasticity retains this stress.However,we find that some anomalous results will appear after the local stress is kicked out from peridynamics.By analyzing the local uniaxial tension and the dispersion of elastic wave,we compare peridynamics and the physically-based nonlocal elasticity.Some conclusions are summarized as follows:

(1) In the framework of generalized function,the mutual transformation can be accomplished between peridynamic and the physically-based nonlocal model of elasticity if the micro-modulus differs from the nonlocal kernel by a second-order gradient term of the Dirac delta function.

(2) Compared with the physically-based nonlocal model of elasticity,the peridynamic solution of the local uniaxial tension always contains a singular Dirac function.This singularity is likely due to the lack of local stress.

(3) Peridynamic wave and PNE wave are all dispersive,but the dispersion of peridynamic wave is anomalous.The peridynamic wave will be cut off when the frequency exceeds the maximum at the dispersion curve.Meanwhile,the negative group velocity also occurs in the peridynamic wave.We think that this anomalous dispersion also stems from the lack of local stress.

In a word,the singularities of peridynamic solutions and anomalous dispersion may be caused by the lack of local stress to a considerable degree.However,if the local stress is introduced,just as same as Eq.(11),the advantage of peridynamics to handle problems with discontinuities will be lost.Consequently,a question is whether there is a model in which these anomalous results can be removed but the advantage of peridynamics is still retained.This question awaits further exploration.

Acknowledgement:The support of the National Nature Science Foundation of China through the Grant No.11672129 is gratefully acknowledged.

Appendix A

The key to the Fourier transform of Eq.(13)consists in determiningC0(x)u(x).It can be given by the multiplication theorem as follows

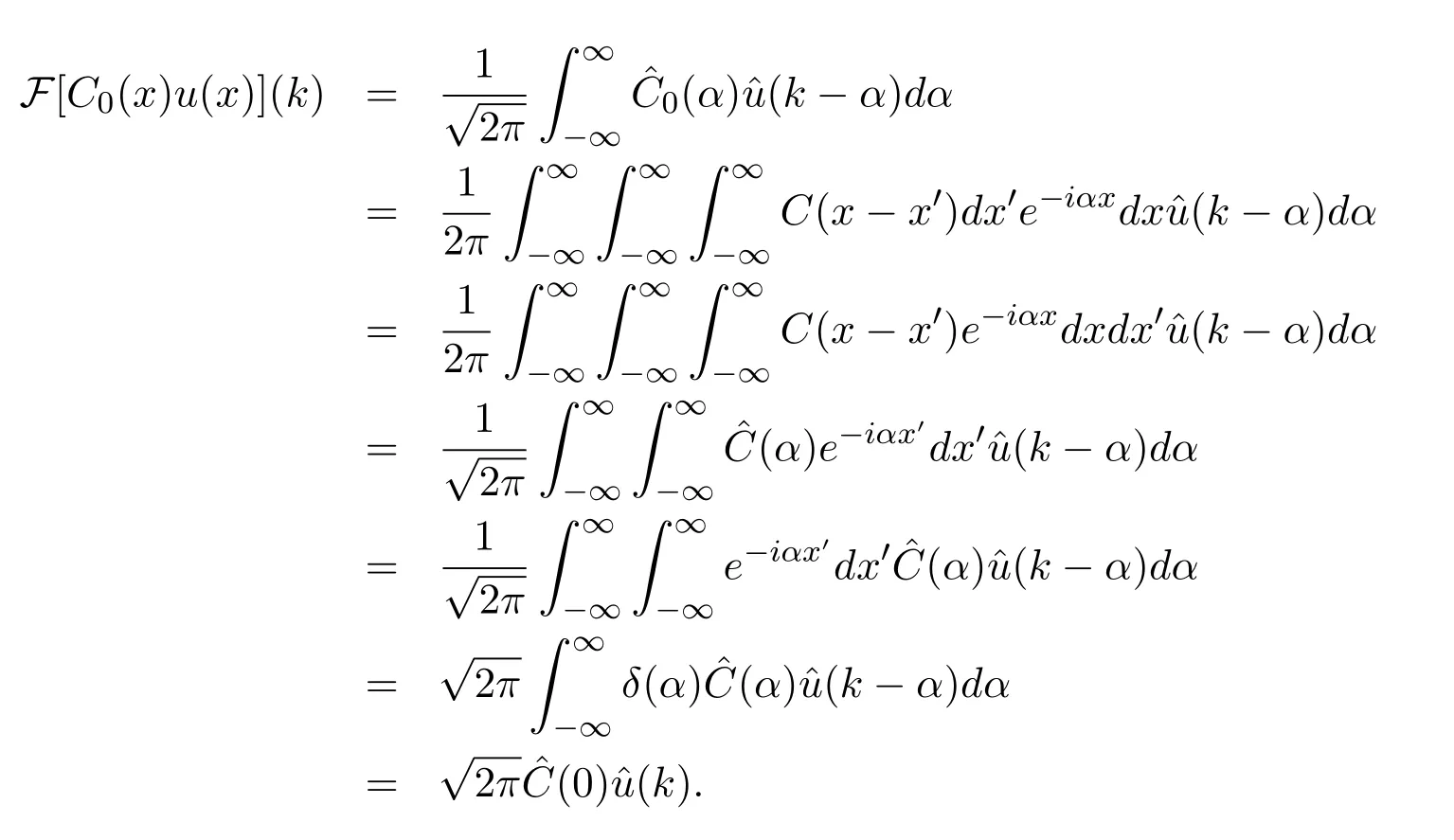
Appendix B

For the two-point tension,the governing equation of classical elasticity is written as

which can be derived from Eq.(14)by lettingC(x)=Ed2δ(x)/dx2.This shows that the classical elasticity is a limit case of peridynamics.The Fourier transform of Eq.(B1)leads to

Applying the inverse Fourier transform to Eq.(B2)yields Eq.(26).