A Dual-Support Smoothed Particle Hydrodynamics for Weakly Compressible Fluid Inspired By the Dual-Horizon Peridynamics
Huilong RenXiaoying Zhuang and Timon Rabczuk
1Institute of Structural Mechanics,Bauhaus-Universität Weimar,99423,Weimar,Germany.
2Division of Computational Mechanics,Ton Duc Thang University,Ho Chi Minh City,Viet Nam.
3Faculty of Civil Engineering,Ton Duc Thang University,Ho Chi Minh City,Viet Nam.
Abstract:A dual-support smoothed particle hydrodynamics (DS-SPH) that allows variable smoothing lengths while satisfying the conservations of linear momentum,angular momentum and energy is developed.The present DS-SPH is inspired by the dual-support,a concept introduced from dual-horizon peridynamics from the authors and applied here to SPH so that the unbalanced interactions between the particles with different smoothing lengths can be correctly considered and computed.Conventionally,the SPH formulation employs either the influence domain or the support domain.The concept of dual-support identifies that the influence domain and the support domain involves the duality and should be simultaneously in the SPH formulation when variable smoothing lengths are used.The DS-SPH formulation can be implemented into conventional SPH codes with minimal changes and also without compromising the computational efficiency.A number of numerical examples involving weakly compressible.fluid are presented to demonstrate the capability of the method.
Keywords:Dual-support,conservation law,variable smoothing length,duality,SPH,dual-horizon peridynamics.
1 Introduction
In the field of numerical methods of solving continuum mechanics,various particle-based methods have been proposed,among which include smoothed particle hydrodynamics (SPH) [Lucy (1977)],discrete element method (DEM) [Mishra and Rajamani (1992)],particle finite element method (PFEM) [Idelsohn,Oñate and Pin (2004)],material point method (MPM) [Bardenhagen and Kober (2004)],Peridynamics [Silling (2000);Ren,Zhuang,Cai et al.(2016)] and so on.As one of the most famous particle-based method,SPH was originally proposed in the 1970s for the modeling of astrophysical problems [Lucy (1977);Gingold and Monaghan (1977)].The SPH method has attracted attentions of the researchers from a variety of fields since the beginning of the 1990s,and has been successfully applied to solve problems such as the impact in solids [Allahdadi,Carney,Hipp et al.(1993);Randles and Libersky(1996);Rabczuk and Eibl(2003);Hedayati and Vahedi(2017)],dynamic fracture and fragmentation [Rabczuk,Eibl and Stempniewski (2004)],multiple-phase flows [Cleary (1998);Hu and Adams (2006);Memarzadeh,Barani and Ghaeini-Hessaroeyeh (2018)],free-surface flows in fluid dynamics [Monaghan (1994)],Magnetohydrodynamics [Monaghan (1988);Price and Monaghan (2004)].For a more complete review of SPH,we refer to[Liu and Liu(2010);Ye,Pan,Huang et al.(2019)].
Peridynamics[Silling(2000);Silling,Epton,Weckner et al.(2007);Nikravesh and Gerstle(2018);Zhao,Tang and Xue(2018);Shafiei(2018)]is a formulation of solid mechanics that is oriented toward deformations with discontinuities,especially fractures.Though derived from different physical background,Lagrangian smoothed particle hydrodynamics shows great similarity with the state-based peridynamics [Ganzenmüller,Hiermaier and May(2015)].Peridynamics is regarded as a physics-based method for solid mechanics,and the attempt to solve fluid problem has not been explored.On the other hand,the conventional SPH is restricted by constant smoothing length for all particles,though several numerical techniques have been proposed[Nelson and Papaloizou(1994);Monaghan(2002);Springel and Hernquist (2002)].Variable smoothing length in SPH can significantly improve the numerical efficiency and allows for adaptive analysis.Dual-horizon peridynamics allows variable horizon domain for each point by defining two horizon domains for each point,where the horizon describes the direct force interaction and dual-horizon represents the reaction force interaction.Based on the similarity between SPH and peridynamics,it is possible to apply the dual support (inspired by the concept of “dual-horizon” in peridynamics)in the field of SPH to solve the variable smoothing length problem.
SPH is a Lagrangian method based on the kernel approximation,where the partial differential equations are transformed into integral form with the so-called kernel interpolation technique[Liu and Liu(2003)].The computational domain is represented by a set of particles which carry the physical properties,i.e.,mass,density,velocity,position,pressure and internal energy.The particles move and properties change with the time due to the interactions between neighboring particles.
One constraint on the kernel approximation is that the smoothing lengths are required to be constant for all particles.However,a computationally efficient SPH implementation requires locally refined regions where variable smoothing lengths can be used.In order to introduce variable smoothing lengths,several methods have been proposed e.g.,the averaged kernel method [Hernquist and Katz (1989)] or correction methods with∇h[Nelson and Papaloizou (1994);Springel and Hernquist (2002);Vacondio,Rogers and Stansby (2012);Vacondio,Rogers,Stansby et al.(2013)].The averaged kernel method uses the averaged smoothing lengths or averaged kernel functions,where the conservation laws can not be satisfied.In the correction methods,the gradient of the smoothing length must be calculated to determine the optimal smoothing length,and a modified coefficient is introduced in all SPH formulations to preserve the conservations laws(more details will be presented in§2).The optimal smoothing length is calculated iteratively,which makes the implementation of SPH more complicated.
The difficulty of varying support domain for SPH arises from that the single support of one particle fails to account for all force interactions with other particles.In contrast with the correction methods aforementioned,we introduce the concept of “dual-horizon” in dual-horizon peridynamics [Ren,Zhuang,Cai et al.(2016);Ren,Zhuang and Rabczuk(2017)] into SPH for varying the smoothing length for each particle.Meanwhile,the dual-support SPH in fluid may be viewed as the fluid version of dual-horizon peridynamics based on the similarity of SPH and peridynamics in solid.
In this paper,we develop a SPH formulation which naturally includes variable smoothing lengths.The formulation named dual-support smoothed particle hydrodynamics(DS-SPH)is simple,satisfies the conservation of linear momentum,angular momentum and energy when variable smoothing lengths are employed.The paper is outlined as following.In§2,the theoretical background of SPH is reviewed.In §3,the concepts of support and dual-support are introduced,based on which we present a general method to reformulate the SPH equations.In§4,we convert the traditional SPH formulation into the dual-support SPH.In §5,the conservations of momentum,angular momentum and energy are proved.In§6,the implementation of DS-SPH is discussed.Three numerical examples are tested to demonstrate the performance of the DS-SPH method in§7.
2 Theoretical background
2.1 Kernel function
Letidenote the point in the global domain Ω;ribeing the current coordinates vector of pointi,Hiis the support domain associated withiwith a radius ofhi.The kernel functionWiis defined as
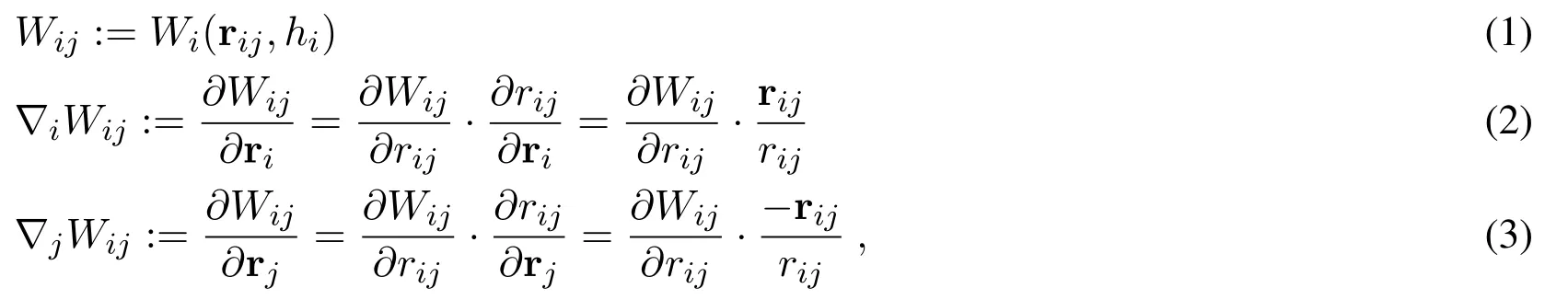
whererij=|rij|,rij= ri -rj.It can be seen that ifhi=hj,Wij=Wji,∇iWij=-∇jWji.There are a wide variety of kernel functions including the Gaussian kernel,cubic-spline,quintic spline or Wendland kernel [Wendland (1995)],to name only a few.For more discussions on these kernel functions,readers are referred to Liu et al.[Liu and Liu (2003);Dehnen and Aly (2012)].As the support in SPH fluid is often defined by the current configuration of the particles,the kernel function is termed as the Eulerian kernel.Aside from the Eulerian kernel,there exists another type of kernel function called Lagrangian kernel whose support domain is based on the material coordinates in the initial configuration.The Lagrangian kernel is capable of overcoming the tensile instability when large deformation is encountered in the context of SPH for modeling solid [Rabczuk,Belytschko and Xiao (2004)].However,the Eulerian kernel is more suitable for fluid simulation compared with the Lagrangian kernel[Rabczuk,Belytschko and Xiao(2004)].
2.2 Kernel interpolation
Kernel interpolation theory starts with the identity

wherefis an arbitrary scalar variable,δis the Dirac delta function andVjis the volume associated with pointj.This integral is approximated by replacing the delta function with a smoothing or kernel functionWwith finite widthhi,e.g.,
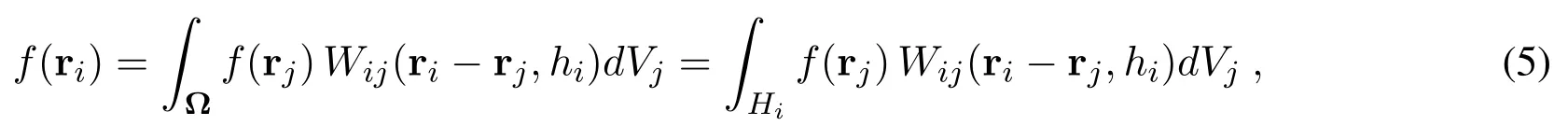
whereWhas the property
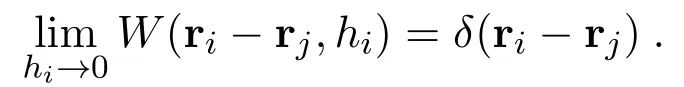
Integration by parts and neglecting all surface terms,the derivative off(ri)is derived as

Hence the derivative of a function is transferred to the kernel function by kernel interpolation theory.
2.3 Completeness of kernel function
The completeness is related to the capability of the kernel approximation to reproduce a polynomial function of certain degree exactly.Zero-order completeness is necessary to represent the rigid body modes while first-order completeness is a necessary condition for constant strain state.According to Belytschko et al.[Belytschko,Krongauz,Dolbow et al.(1998)],first-order completeness is defined by

First-order completeness for the derivatives of the kernel approximation for any particleiin 1,2 and 3 dimensions should satisfy

Here,I is the identity matrix.SPH in its continuous form (or integral form) fulfills zero- and first-order completeness and hence the 'standard' kernel function as given in Eq.(5) is sufficient.However,not even zero-order completeness is guaranteed for the discrete SPH form as shown by Nguyen et al.[Nguyen,Rabczuk,Bordas et al.(2008)].Therefore,many correction methods have been developed such as the symmetrization proposed by Monaghan [Monaghan (1988)],Randles &Libersky correction [Randles and Libersky (1996)],Johnson &Beissel correction [Johnson and Beissel (1996)] and Krongauz-Belytschko corrected derivatives [Krongauz and Belytschko (1997)].In the current paper,two of those approaches are briefly summarized.
The gradient correction of kernel function [Bonet and Lok (1999)] in discrete form satisfying Eq.(8)is

where ΔVj=mj/ρj.The gradient correction guarantees the conservation of angular momentum.The zero-order(Shepard filter)is given by

Such correction is often adopted to reduce the pressure oscillations for particles near the boundaries or close to free-surfaces when density summation is used instead of the continuity equation.Based on Eq.(10),the kernel gradient correction (or corrected derivatives method)is given by
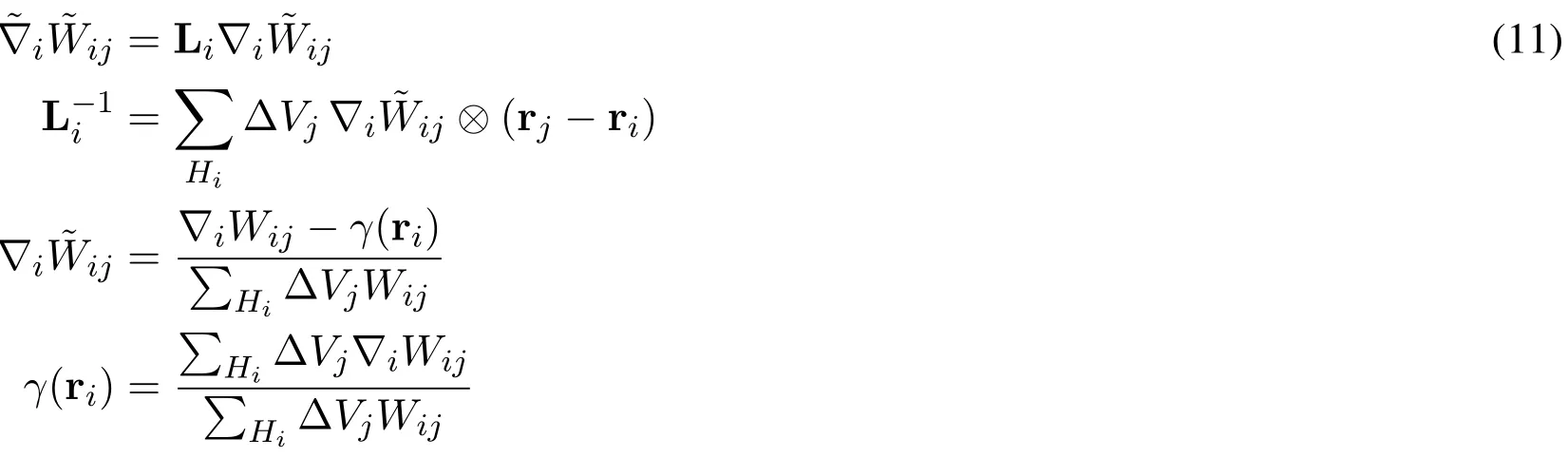
where ΔVj=mj/ρj.It is not difficult to verify that both Eq.(9)and Eq.(11)satisfy Eq.(8).
The gradient correction Eq.(9) is much simpler than the mixed correction Eq.(11).In the current paper,the gradient correction is employed.The formulations with zero-order correction or gradient kernel correction are straightforward in SPH.It requires only the replacement of the kernel functions with their associated corrected kernels,i.e.,Wij →andorSubsequently,we derive all equations based on thestandardSPH formulation but the equations for the associated correction methods are straight forward.
2.4 Variable smoothing length in SPH
There are several methods to deal with the variable smoothing length issue.The first method is the averaged kernel function[Hernquist and Katz(1989)]given by
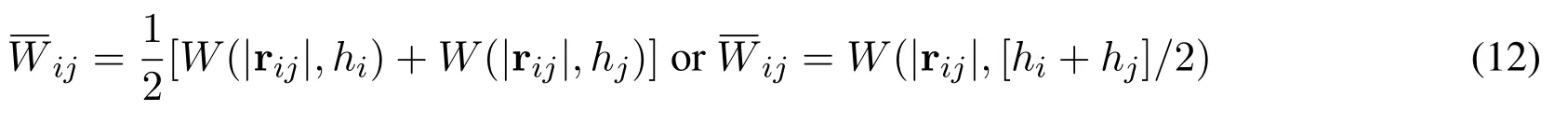
The averaged kernel between paired particles with different smoothing lengths guarantees the anti-symmetrical pair-wised forces and thus preserves the symmetry of the particle interactions[Liu and Liu(2003)].The second method is based on the correction term∇h[Nelson and Papaloizou(1994);Springel and Hernquist(2002);Vacondio,Rogers,Stansby et al.(2013)]in the equations of motion.The key idea is to relate the local number density of particles with the smoothing length and to keep the variable inside the smoothing sphere constant[Springel and Hernquist(2002)],i.e.,
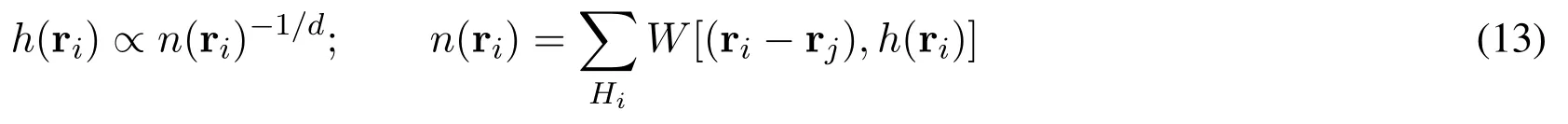
The equation of motion in Springel et al.[Springel and Hernquist(2002)]is w
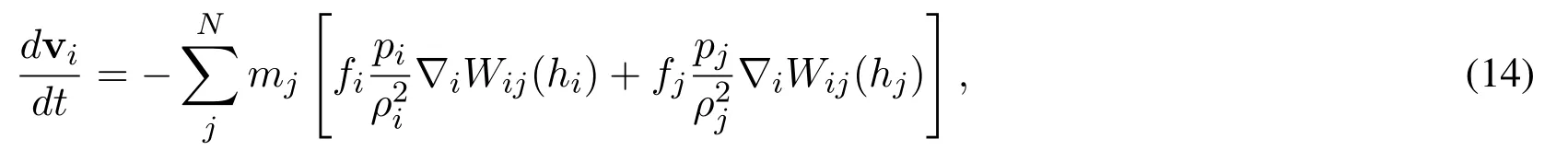
hereNis the number of all particles,piis the pressure andfiis defined as

The quantitiescan be computed along with the densities themselves;more details are found in Springel et al.[Springel and Hernquist(2002)].
Monaghan[Monaghan(2002)]proposed a similar formulation for the smoothing length.In his work,the momentum equation is
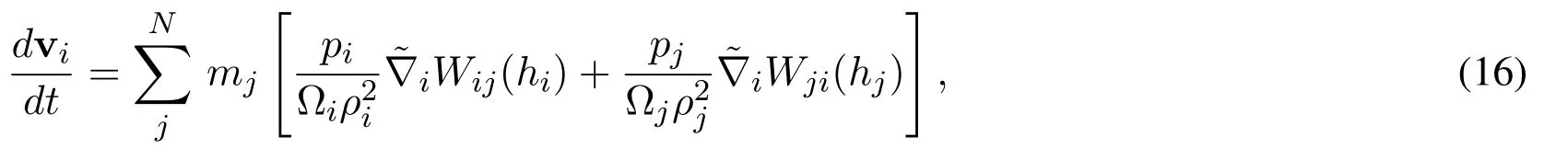
where Ωiis given by

The coefficient Ωiis also introduced in the continuity and energy equations.Both expressions in Eq.(15) and Eq.(17) are related to the term∇hi.The basic idea is to find the proper valuehiwhich satisfies Eq.(13).In order to find the desirable smoothing length,Eq.(13)is transformed into a set of two simultaneous equations which is computed at the location of particlei,
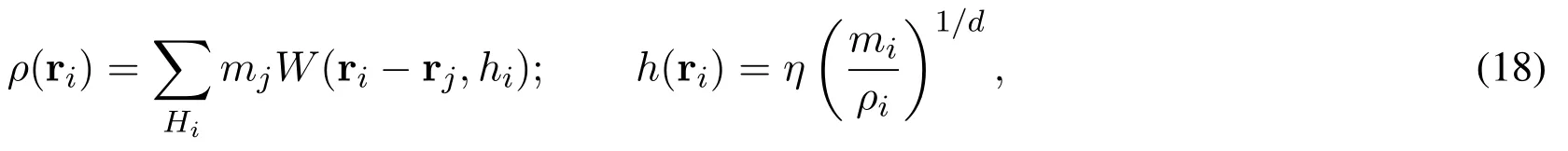
whereηis a parameter specifying the smoothing length in units of the mean particle spacing (m/ρ)1/d,dis the number of dimensions.These two equations can be solved simultaneously using standard root-finding methods such as Newton-Raphson or Bisection[Price(2012)].However,this inevitably increases the computational cost and make the SPH implementation more complex.
3 Support domain and dual-support domain
In this section,the key concepts of support and dual-support are presented and the duality of dual-support is proved.The new concept provides great flexibility to convert the traditional constant support SPH to dual-support SPH allowing for variable smoothing length for each particle.
3.1 Support and dual-support
The conventional SPH formulations based on variable smoothing lengths consider the unbalanced interaction with averaged kernel functions,correction terms∇h.The basis of all these methods is a single support domain.However,the single support domain cannot elegantly resolve the unbalanced interaction with different support radii.In SPH with variable smoothing lengths,one common situation as shown in Fig.1 is thatj ∈Hi,i /∈Hj.The unilateral interaction violates the Newton’s third law.Therefore,a single variable support is not sufficient to define the interactions between particles and the new concept of support and dual-support is introduced subsequently.A similar concept is the“dual-horizon”in peridynamics[Ren,Zhuang,Cai et al.(2016)].
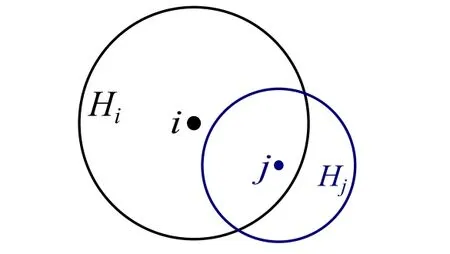
Figure 1:Two points with different support domains. j ∈Hi,i /∈Hj
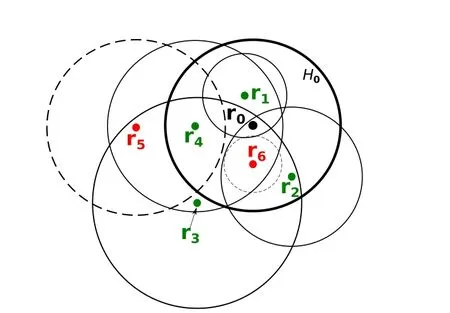
Figure 2:The support and dual-support for point 0,H′0 ={1,2,3,4,H0} ={1,2,4,6},where circles denote support domains
Support
The supportHifor pointiis defined as a domain related toi.When the domain is centered atiwith a radius ofhi,the supportHican be given as

In traditional SPH,the support of a particle is a domain where the kernel function is positive(see p60 in Liu et al.[Liu and Liu(2003)]).The definition in Eq.(19)implies the positivity of kernel function since the kernel function is calculated in the support,and the kernel function is zero outside of the support domain.Therefore,the support in Eq.(19) is the same as that in conventional SPH.Dual-support ofiis defined as a union of the points whose support domain includesi,denoted by

In the notation of dual-supportH′i,the superscript prime indicates“dual”,and the subscriptidenotes the object particle.When the support is defined as circle or sphere centered at that point,i’s dual-support can be expressed as

For any pointi,the shape ofH′iis arbitrary and depends on the sizes and shapes of supports as well as the locations of the particles.For example,as shown in Fig.2,the dual-support with respect to point 0 contains particles {1,2,3,4},whose supports are denoted by thin solid circles.Particles{5,6} are not included in the dual-support of point 0 since their supports do not include point 0.For case with constant smoothing length,asj ∈Hi ⇔i ∈Hj,H′iis equal toHiand then support and dual-support degenerate to the constant support in traditional SPH.
It is worth mentioning that the dual-support domain with respect to the support domain is similar to the relation between the influence domain and support domain in meshfree methods [Hernquist and Katz (1989);Liu and Liu (2003)].The dual-support domain actually represents the influence domain.However,to the authors’knowledge,the duality of the influence domain and support domain was not identified in the literature.In the conventional SPH formulation,either the support domain or the influence domain is employed.In our study,the influence domain and the support domain should be employed simultaneously in the SPH formulation when variable smoothing lengths are used.For the simplicity of derivation,we use the dual-support domain to represent influence domain.
3.2 The duality of dual-support and support domain
LetF(i,j)be any expression depend on two pointsi,j.The duality of dual-support-which we have proven in Ren et al.[Ren,Zhuang and Rabczuk (2017)]-states that the double integral of the termF(i,j)in dual-support domain can be converted to the double integral of the termF(j,i)in support domain:
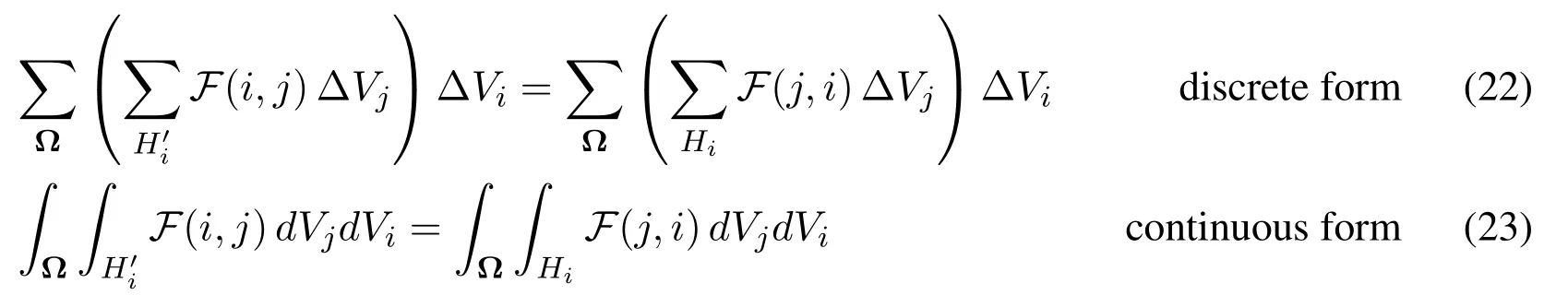
The key idea lies in the fact that the termF(i,j) can be both interpreted inHiandHj′.For the sake of completeness,the proof of duality of dual-support is provided in Appendix A.
3.3 The dual formulation based on support and dual-support
Letρbe any scalar,fbe any scalar field.The SPH formulation ofcan be obtained as
In order to derive the DS-SPH formulation,we simply exploit the duality,Eq.(23),and replace the integral over the support of the first term in Eq.(25)with the integral over the dual-support:

This obviously yields the DS-SPH formulation:
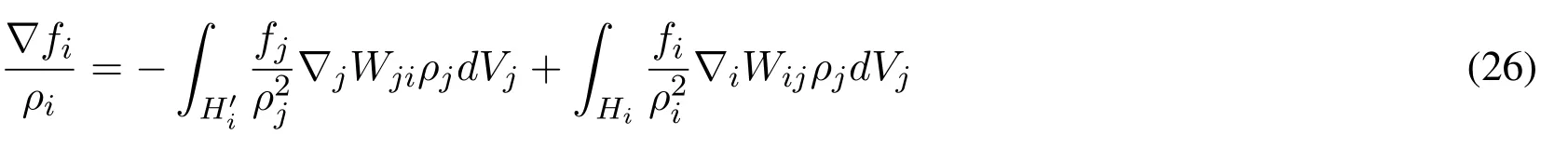
Note that for points with identical smoothing length,hi=hjleads toHi=H′iand∇iWij=-∇jWjiin Eq.(25).Eq.(25)forms the key step to convert traditional constant support SPH to dual-support SPH.Letφbe any scalar and A be any vector.With the operation defined in Eq.(25),the following dual support formulations can be devised
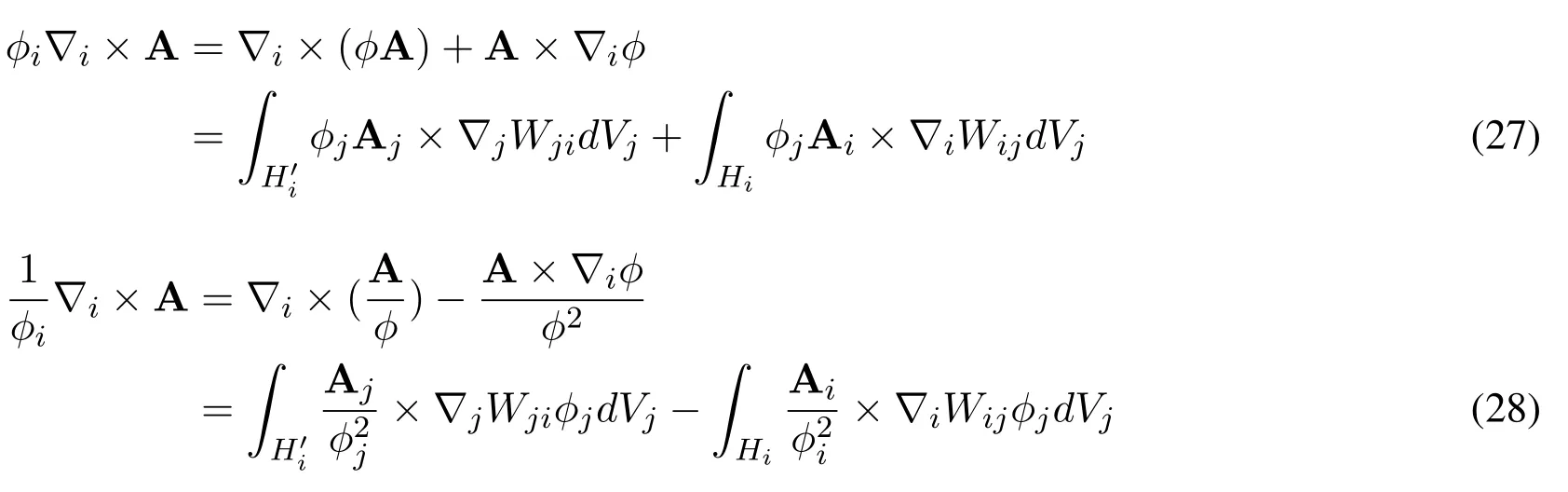
The second order derivative can be obtained in a similar way.One expression recommended by Brookshaw et al.[Brookshaw(1985);Morris,Fox and Zhu(1997)]for second derivative is
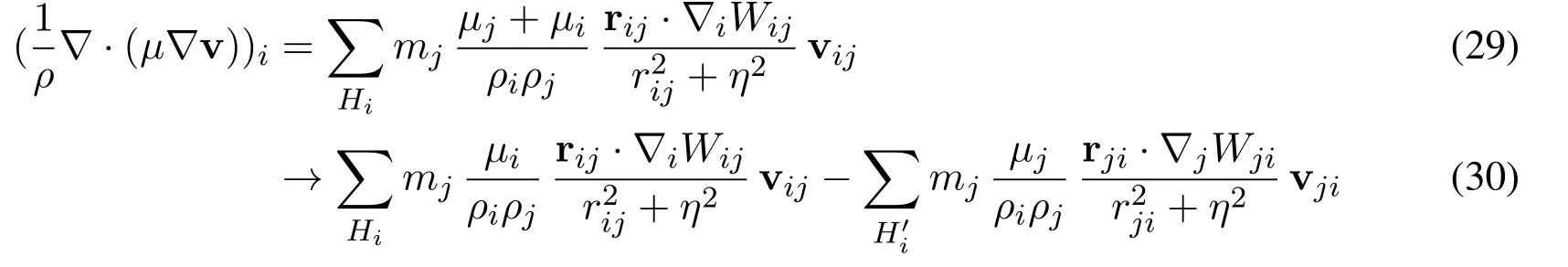
which requires only first spatial derivatives,where vij= vi -vj,ηis a small number introduced to avoid a zero denominator during computations and is set to 0.1h.Eq.(29)is the combination of SPH formulation of first derivative and first order finite difference.
4 Dual-support smoothed particle hydrodynamics
In this paper,we apply the dual-support formulation to fluids.The application of DS-SPH in solid is refereed to Dai et al.[Dai,Ren,Zhuang et al.(2017)].The Lagrangian form of the fluid dynamics equations is given as
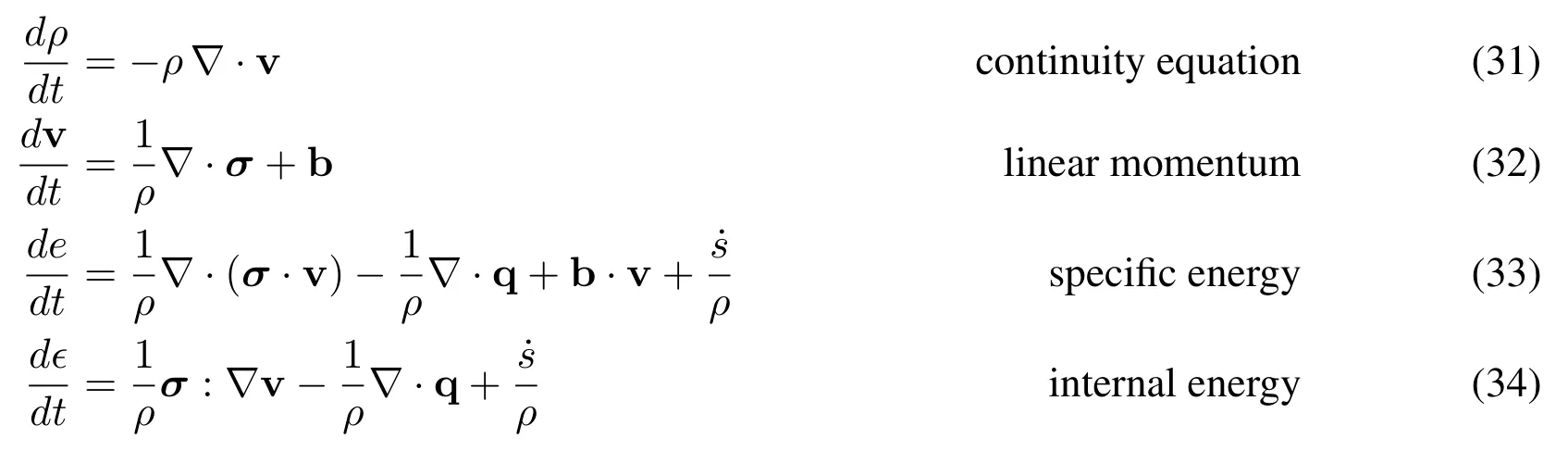
whereis the material time derivative,σthe Cauchy stress;q =-κ∇Tthe heat flux density vector,κthe thermal conductivity,Tthe temperature,˙sthe source term;b the body force density,dthe internal energy density,the specifci energy per unit mass.Eq.(33)and Eq.(34)are equivalent.Two constitutive models for the fluid are
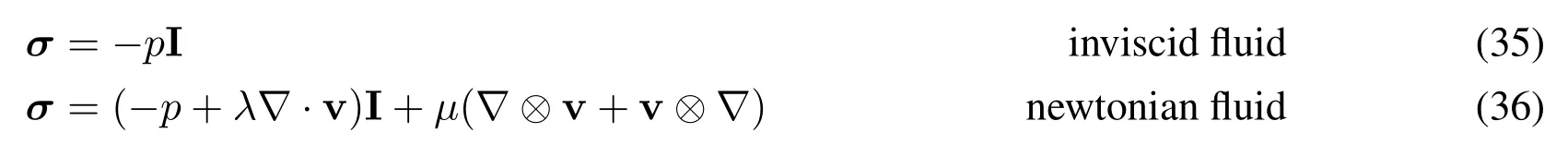
wherepis the pressure;µis the dynamic viscosity,andλis the second coefficient of viscosity.As a detailed derivation of the SPH equations is provided elsewhere,see e.g.,[Liu and Liu(2003)],we omit it in this manuscript.The continuity equation in SPH form is given by[Liu and Liu(2003)]

In the Lagrangian formulation,the conservation of mass is naturally satisfied,hence we are not going to recast the continuity equation into the dual-support formulation.The continuity equation is often replaced by the summation density approach

4.1 SPH formulation with dual-support
It can be shown [Randles and Libersky (1996)] that the SPH formulation with constant smoothing length for the equation of motion is given by
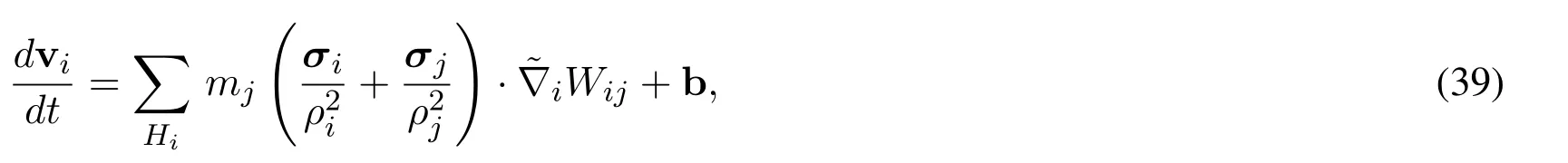
and the energy equation by
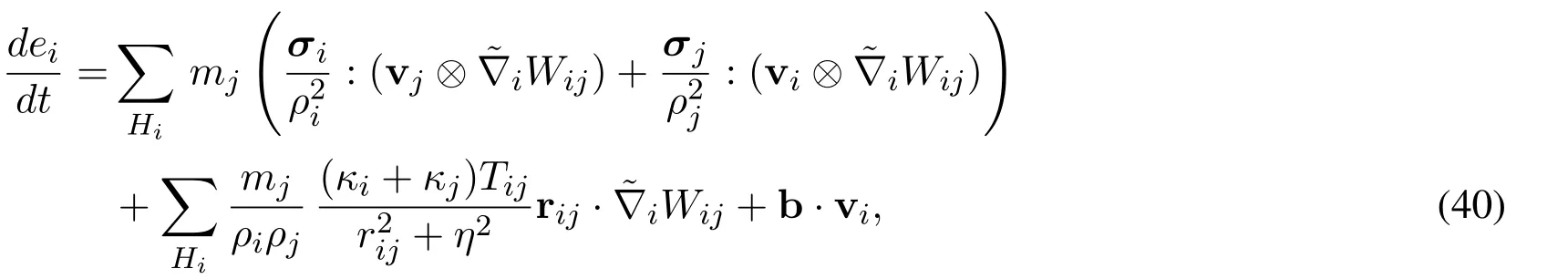
where the term on heat conduction is similarly expressed by Eq.(30).
Eq.(40)can be simplified via the momentum equations Eq.(39),which leads to the energy equation based on the internal energy
In order to allow variable smoothing lengths,applying the procedure in Eq.(25)-Eq.(39),Eq.(40)and Eq.(41),we obtain the following dual-support formulations for the equation of motion and energy equations,
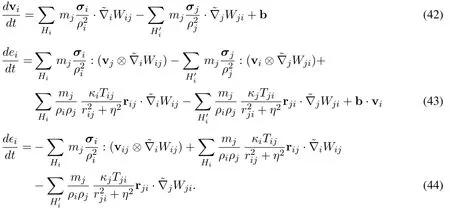
4.2 Two special cases
For fluid with material constitution given by Eqs.(35),(42) and (44) can be further simplified into,respectively
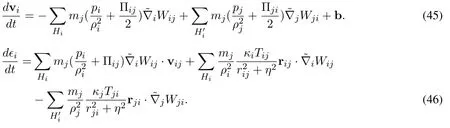
where Πijis the artificial viscosity,which is necessary to model strong shocks and prevent particles from interpenetration [Benz (1990)] in the absence of physical viscosity and is given by
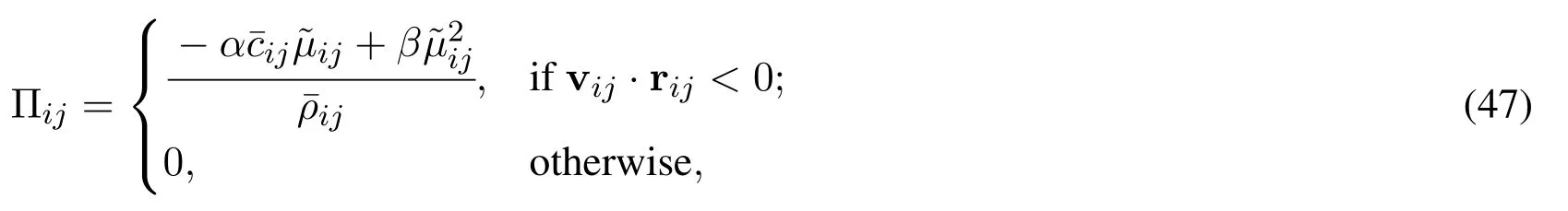
When all support radii are constant,the dual-support domain is identical to the support domain,then Eqs.(45)and(46)degenerate to the traditional SPH with artificial viscosity(e.g.,[Liu and Liu(2003);Gomez-Gesteira,Rogers,Dalrymple et al.(2010)]).
Another viscosity in fluid is the physical viscosity.When the artificial viscosity in Eqs.(45)and (46) is replaced with the physical viscosity using Eq.(30),SPH can be reformulated as,
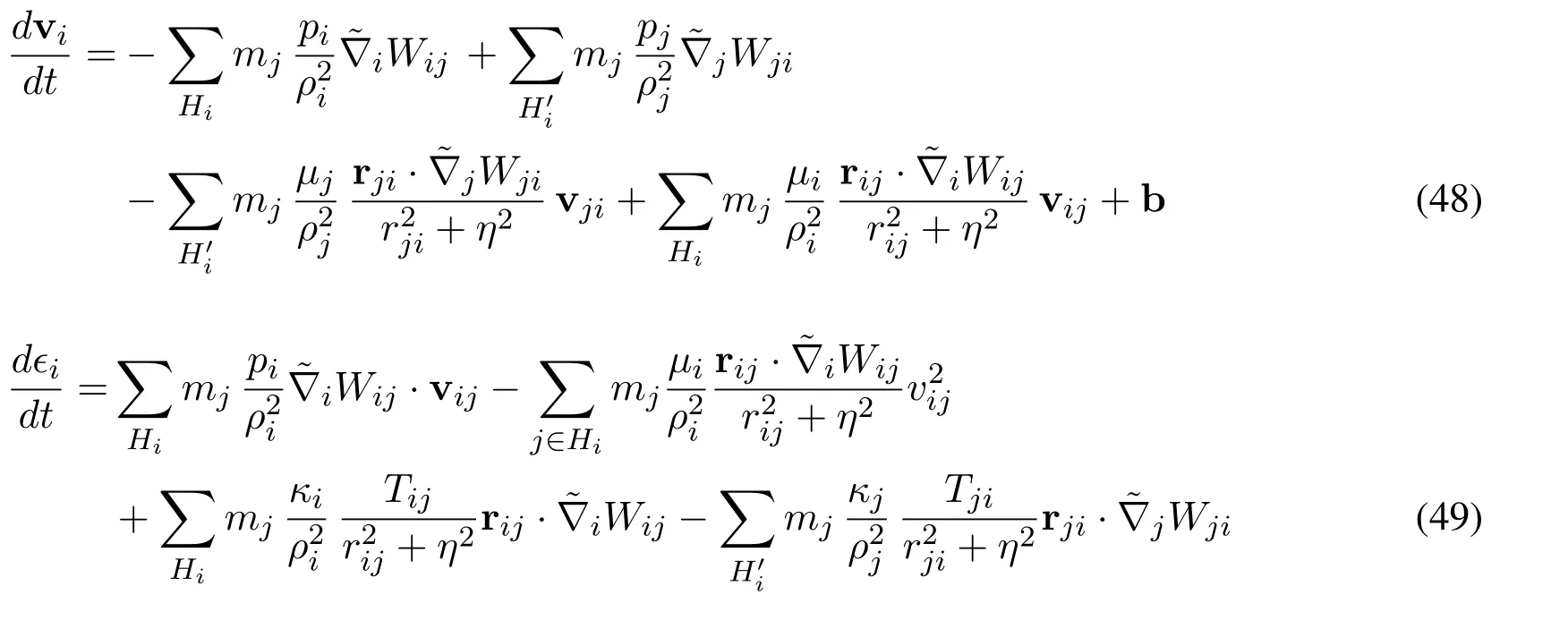
5 Conservation of the basic laws
In this section,the conservation laws,i.e.,the linear momentum conservation,angular momentum conservation and energy conservation,in DS-SPH are discussed.Due to the Lagrangian description of motion,the total mass is conserved naturally as pointed out previously.
5.1 Conservation of linear momentum
The conservation of momentum requires
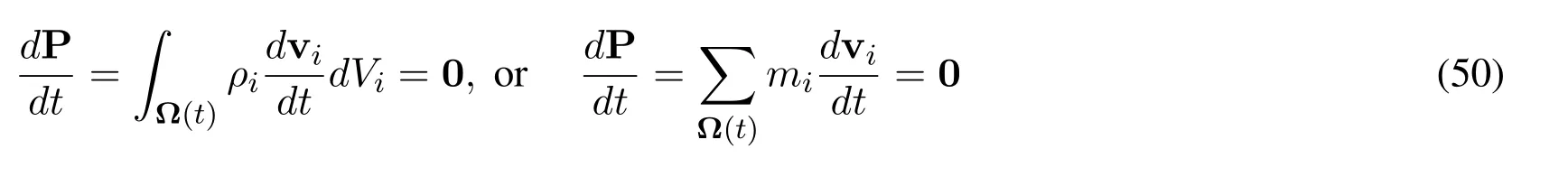
which represent the continuous form and discrete form,respectively.The variation of momentum is derived as
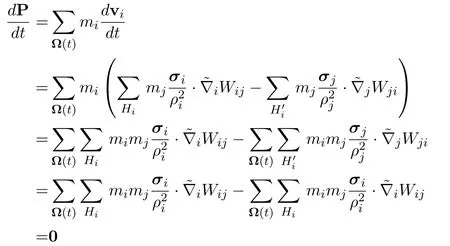
In the fourth step,the duality of dual-support is used.Therefore,the conservation of momentum is satisfied.
5.2 Conservation of angular momentum
The conservation of angular momentum requires
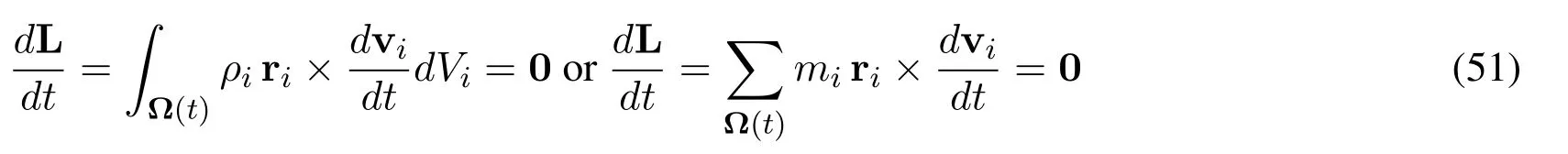
In the proof of angular momentum,we replacein momentum equation withThe variation of angular momentum is derived as
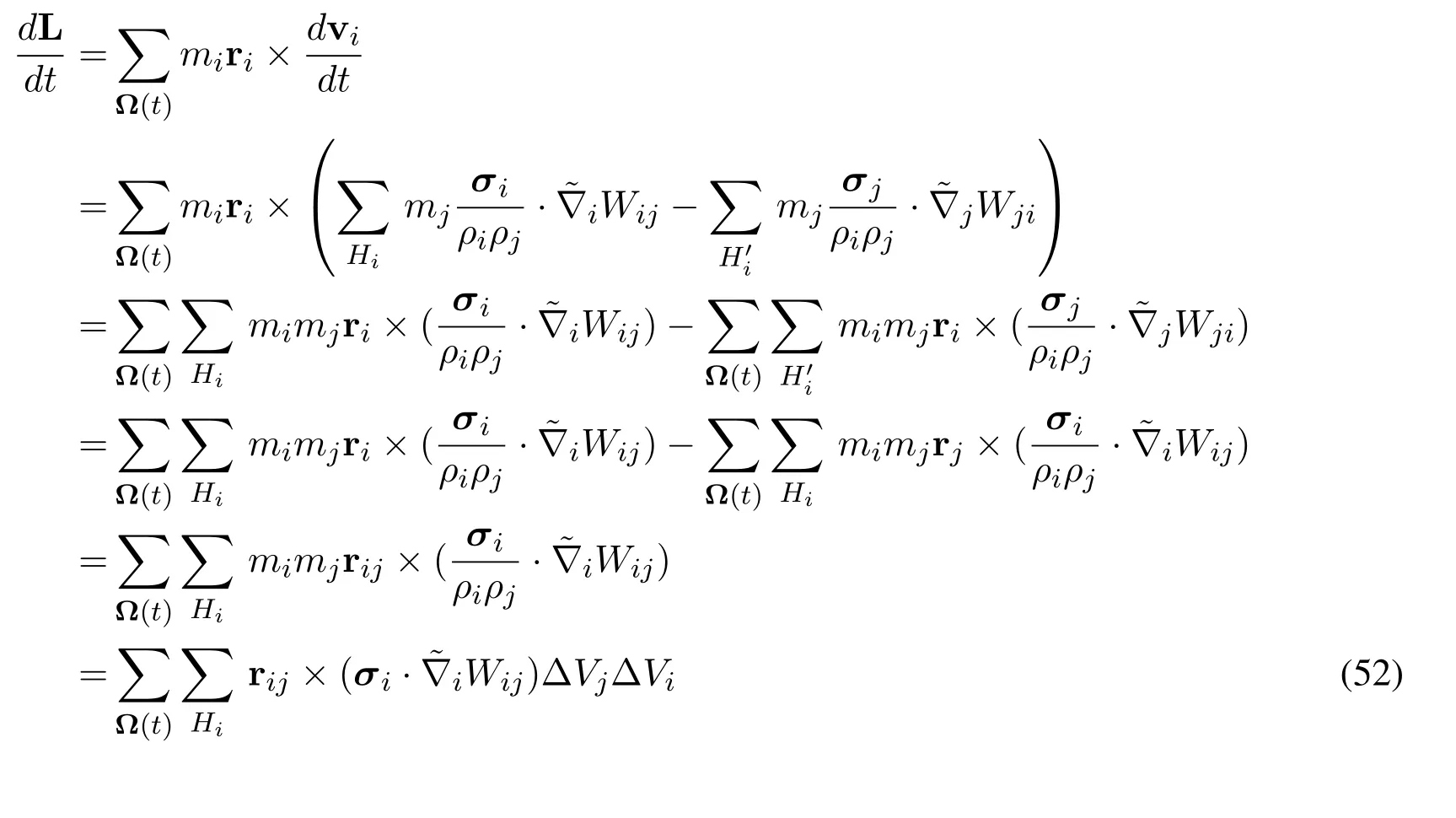
In the fourth step,the duality of dual-support is used.Temporally,for the sake of simplicity,we abbreviateHi →H,ΔVj →ΔV,rij →r,Wij →Wandσi →σ.Let capital lettersI,J,K,Lbe the dimensional index.
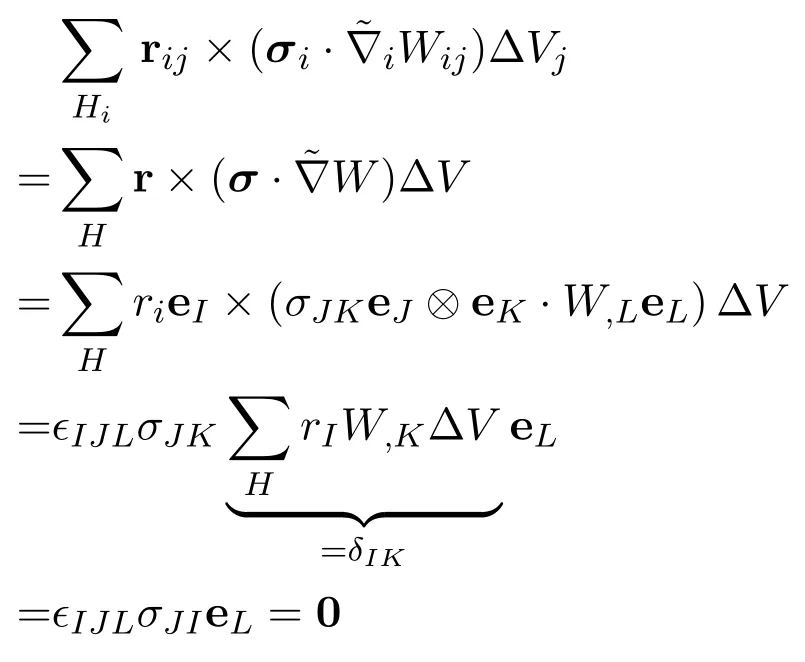
wheredIJLis the permutation symbol andrIrefers to the I-th component of r,is the function with gradient correction,and the symmetry of the Cauchy stress tensorσand the completeness ofWijare used.Therefore,Eq.(52)is zero,and the angular momentum is conserved when the linear completeness is satisfied.
5.3 Conservation of energy
The conservation of energy requires
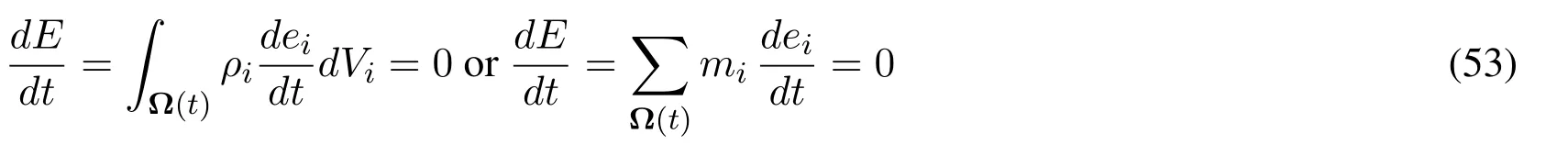
The variation of specific energy is derived as
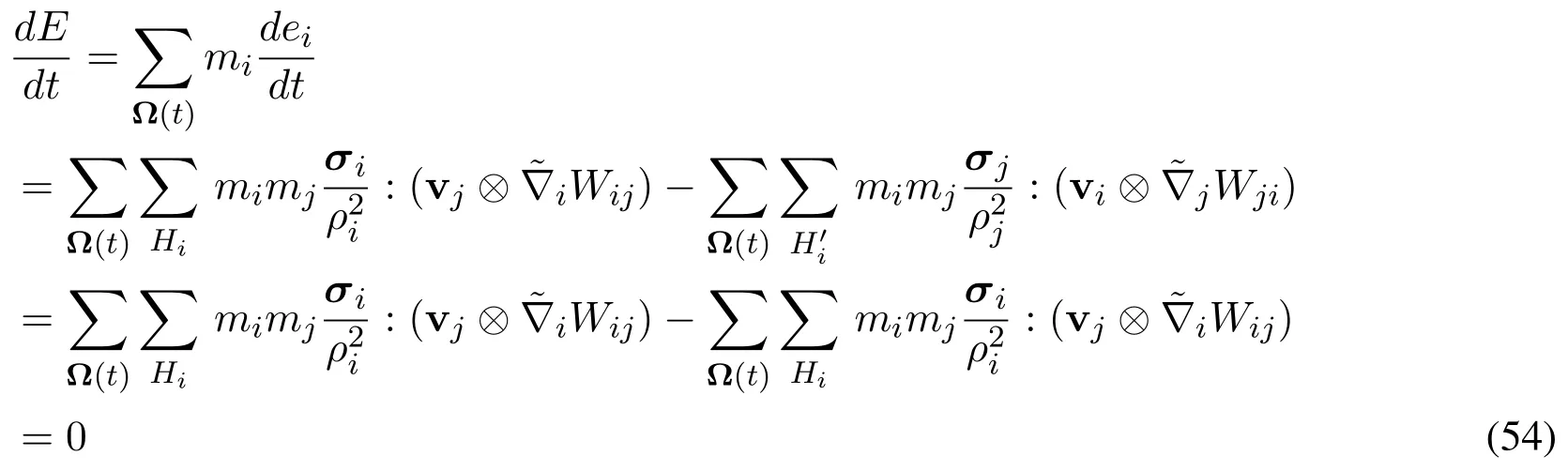
In the third step,the duality of dual-support is used.So the specific energy is conserved.
6 Implementation of DS-SPH
At each step,the values at stept+Δtare calculated based on the known variables as rti,vti,fti,ρti,dti,˙ρti,˙dti.Many numerical schemes can be used to integrate the SPH formulation,e.g.,the Leap-frog prediction-correction scheme and the Verlet-velocity scheme[Verlet(1967)].
When the energy equation is considered,the Leapfrog prediction-correction scheme is preferred.The Leapfrog prediction-correction scheme comprises three steps as below
1.Prediction step
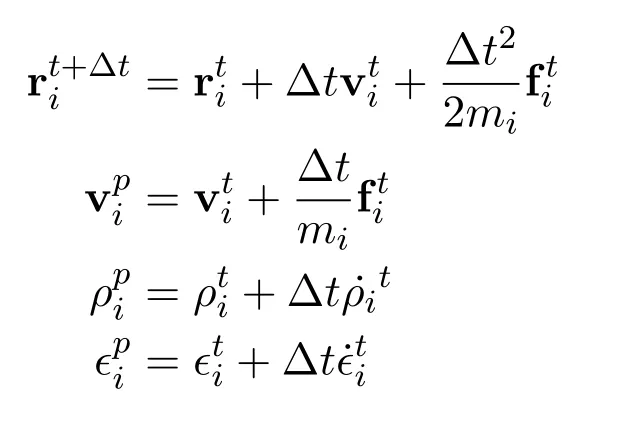
3.Correction step
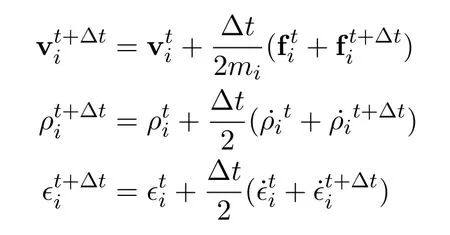
DS-SPH requires the summation over the support and dual-support for each particle.However,the forces from the dual-support domain are obtained from other particles’support domains.For any particlej ∈Hi,the force fijfor pairijis calculated and added to particlei.Sincej ∈Hi ⇔i ∈H′j,-fijis the force from dual-supportH′jof particlej,thus it can be added to particlej.Hence,when summing over all other particles,the forces fromH′iare automatically calculated.In other words,the force from one particle’s support domain is reusable for the other particle’s dual-support domain.
Let us consider Eq.(45).In the implementation,we loop over all particlesj ∈Hiand add the forceto particlei.Sincej ∈Hi ⇔i ∈Hj′,we can simply add-fijto particlej.In contrast,traditional SPH requires computing-mj(++Πij)Wijwhen loopingj ∈Hi,and calculating-when loopingi∈Hj.Hence,DS-SPH is more efficient compared with the traditional SPH.
In contrast with the kernel average method which depends on two particles’ kernel functions,any particle in DS-SPH only concentrates on its own kernel function and support domain,which is independent with the other particles.Eq.(18) indicates that the smoothing length is inverse proportional to the density.Let Δxidenote the 'size' of particlei.Without loss of generality,we assume that the shape of the particle is a cube in 3D or square in 2D.

wheren ≈1.5~3.It can be seen that the smoothing length decreases with increasing particle density;the low(high)density,which indicates relatively sparse(dense)neighbors,causes the support domain to expand(shrink)adaptively.
7 Numerical examples
7.1 1D heat conduction
Consider a 1D bar of with lengthL=50 cm.The bar is discretized with a particle spacing of Δx=1 cm or Δx=0.5 cm;the heat diffusion coefficient isα=1.0×10-4m2s-1.The left half is assigned an internal energy ofe0l= 1 J/m,the right halfe0r= 2 J/m.The total energy in the 1D bar isEtotal=0.75 J.There is neither potential nor kinetic energy present in this simulation.The only non-zero contribution is the total internal energy.The energy profile given by

is compared to the analytic solution at 4.0 s.Three cases as shown in Tab.1 are considered.The first case is modeled by conventional SPH with constant smoothing length.The second case is simulated by conventional SPH with variable smoothing lengths but without additional treatment.The third case is implemented with our dual-support SPH.In order to test the influence of the transition of smoothing length,two particle spacings Δx=1 cm,Δx=0.5 cm in Case II and Case III were employed,more specific,the particle spacing in the interval ofx= 0.3L-0.5Lis Δx=0.5 cm.TheL2error in internal energy is given by

with
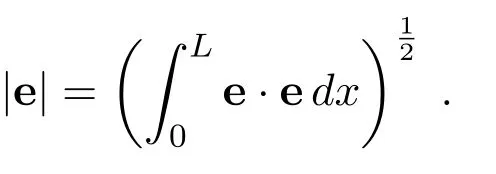

Table 1:The parameters of three cases
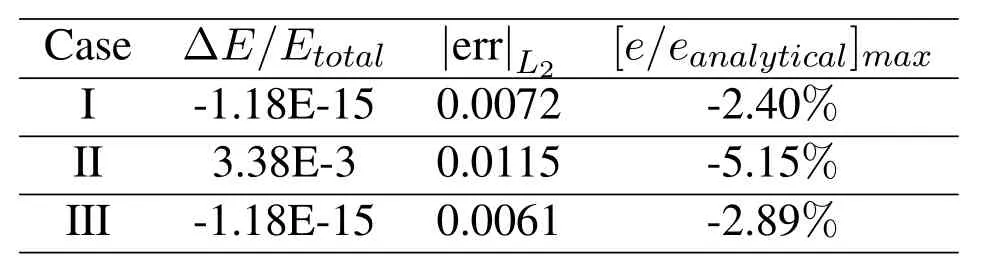
Table 2:The results of three cases for t = 4 s
The numerical results agree well with theoretical solution,as shown in Tab.2.The error of the conventional SPH formulation with varying smoothing length is roughly twice as high as the error with the dual-support SPH version.
7.2 Waterdropletflow
In this section the flow simulation of an elliptical water droplet is presented.The main purpose of this example is to demonstrate that the total linear and angular momentum are conserved for the dual-support SPH in the absence of external forces.This example is tested by two formulations,one is the Eq.(39) with only one varying support for each particle (namely,single support SPH),the other is Eq.(42) (dual-support SPH).No treatment of varying support radii is employed for the first formulation.The gradient correction of kernel function (cubic-spline kernel) is employed in two formulations.The continuity equation Eq.(31) is calculated directly by the divergence of velocity.The velocity gradient is calculated by

The geometry of the bubble is a circle of 1 m radius without external forces but with initial velocity field of(-100x,100y)m/s.The bubble is discretized with 1979 particles,whose distribution is shown in Fig.3.The cell’s volume represents the particle’s volume.In order to test the influence of variable smoothing lengths on the conservation laws,the upright part of the bubble is discretized with small particles.The initial smoothing length is selected as two times of the particle size,i.e.,hi= 2Δxi.The particle size is estimated by assuming the shape of square.
The total stress is calculated by Eq.(36).The pressure is calculated by the following equation of state for water[Monaghan(1994)],
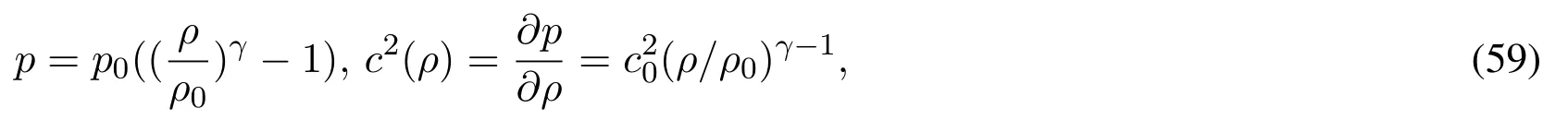
whereγis a constant;γ=7 in our simulations;ρ0is the reference density,c0=1400m/sis the sound speed at the reference density.p0=c20ρ0/γis the artificial bulk modulus[Morris,Fox and Zhu(1997)].In this example,the artificial bulk modulus isp0=285.714 MPa,viscosity coefficientsλ=0 andµ=0.5 kg m-1s-1,initial densityρ0=103kg/m3.Within the simulations,the shape of the bubble should remain elliptical,the value ofab(semi-major axis×semi-minor axis)should remain constant.The analytical solution ofbvarying with time can be obtained as

andwis the initial value ofab.
Fig.4 shows the geometry of the water droplet simulated by single support SPH and the dual-support SPH.The result by DS-SPH agree well with the theoretical shape denoted by solid lines,while the result by traditional SPH using only one support domain is affected by the particle distribution.The reason is that the traditional SPH formulation is only suitable for constant smoothing length;when encountering the variable smoothing length,the accumulated unbalanced forces drive the final result away from the theoretical solution.In addition,when tracking the total linear momentum(Fig.5),and total angular momentum(Fig.6),the results by single support SPH change significantly with time,whereas that by dual-support SPH fulfill all conservation laws.The non-zero initial total momentum and angular momentum are due to the unsymmetrical discretization.The variation of linear momentum and angular momentum for single support SPH is due to the variation of the smoothing length for each particle at every 50 steps.

Figure 3:The particle discretization of water droplet.Each cell represents one particle
7.3 2D dam break over dry bed
The dam breaking experiment,which was described in Koshizuka et al.[Koshizuka and Oka (1996)],is a benchmark problem to test the accuracy of SPH code by Violeau et al.[Violeau and Issa (2007)] and Crespo et al.[Crespo,Gómez-Gesteira and Dalrymple(2007)].The tank is 4 m long,the initial volume of water is 1 m long and its height 2 m,as shown in Fig.7.The system is solved with a leapfrog prediction-correction scheme,using a cubic-spline kernel without kernel gradient correction,specular reflection boundary condition by Eq.(61),artificial viscosity,α= 1,β= 1.The density is calculated by Eq.(37).Fluid particles were initially placed on a staggered grid with zero initial velocity.In order to employ a large time increment,the sound speed is set as 100 m/s,which is 10 times larger than the maximum flowing speed.The specular reflection boundary is given by

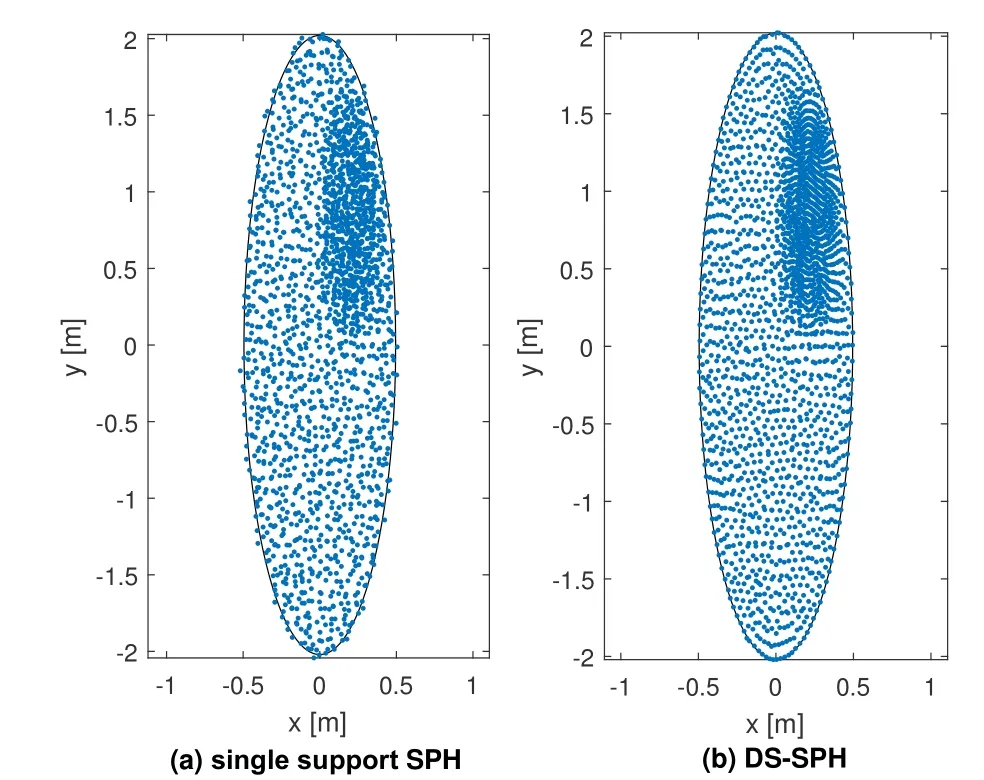
Figure 4:The geometry of water droplet at t = 8×10-3 s.The solid line represents the theoretical shape
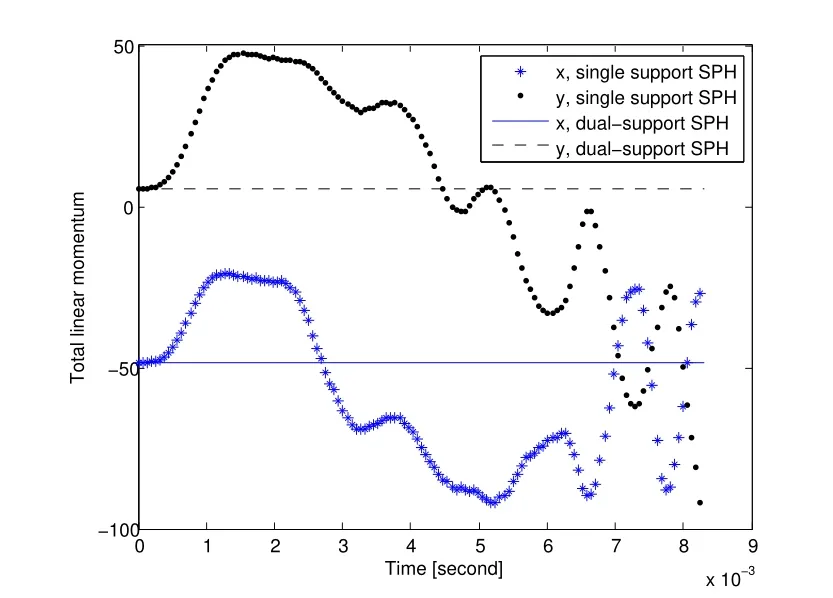
Figure 5:The total linear momentum against time
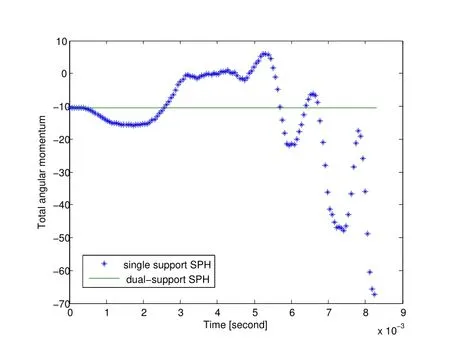
Figure 6:The total angular momentum against time
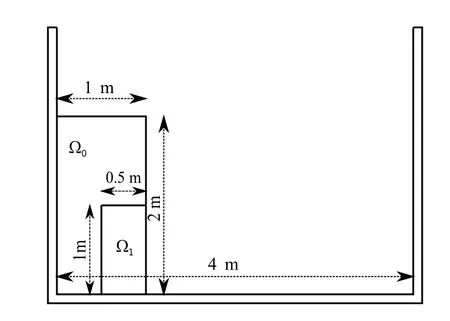
Figure 7:Initial configuration of the water column and the tank
where v denotes the velocity,n is the inward normal direction of the wall at that point.Note that the specular reflection boundary only changes the direction of the particle’s velocity when the particle is approaching the boundary,thus the kinetic energy is not affected.Such good property enables us to track the global energy during the simulation.Although the equation of state given by Eq.(59)is irrelevant to the energy state,the energy equation Eq.(46)is considered in order to track the internal energy since the artificial viscosity converts the kinetic energy into the internal energy.
Three cases are run to shown the capabilities of the dual-support SPH.Case I is based on traditional single support SPH with variable smoothing length and Case II adopts the DS-SPH formulation.Case III uses constant smoothing length during the simulation.The initial smoothing length is set ashi= 2Δxi.The smoothing length for each particle in Case I and Case II is updated with Eq.(55)at every 200 time steps.The particle spacing of Case I (5,600 particles) and Case II (5,600 particles) is Δx= 2.5×10-2m in Ω0,Δx=1.25×10-2m in Ω1,whereas only one particle spacing Δx=1.25×10-2in Case III(12,800 particles).There is a sharp change of smoothing length in the interface of Ω0and Ω1for Case I and Case II.Such transition deteriorates the traditional single support SPH,while dual-support SPH can reduce the adverse effect.The Case III based on traditional constant support SPH is served as the reference.
As shown in Fig.8,the toe velocity of Case II and Case III agreed well with experimental data,whereas that of Case I was affected by sharp transition of smoothing lengths.
The fluid domain is marked with four colors so that the deformation of the interfaces can be tracked.The deformation of water column for three cases at different time is shown in Fig.9 and Fig.10.For case I,the blue zone pushed the red zone and caused the simulation to deviate far away from the reference results given by Case III;the interfaces became irregular and the blue zone spreaded over the bottom.The results of Case II agreed well with that by Case III;the interfaces were continuous and smooth in all steps.Hence the dual-support SPH can reduce the adverse effect of variable smoothing lengths to minimum.When the front toe hit the right wall,for Case II and Case III,the maximal density variation for front toe is smaller than 2%,as shown in Fig.11,while the density for other parts of the fluid is very close to the initial density.
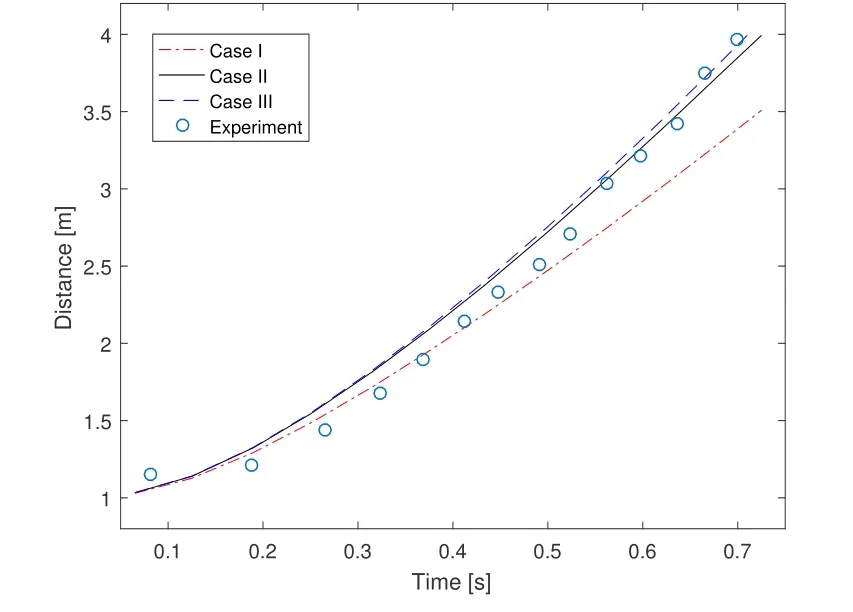
Figure 8:The evolution of dam front toe in experiment[Koshizuka and Oka(1996)]and three cases
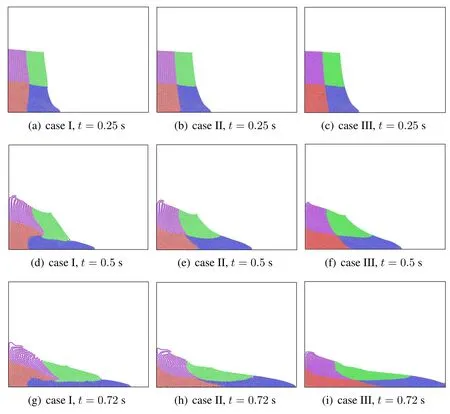
Figure 9:The profile of particles at different time
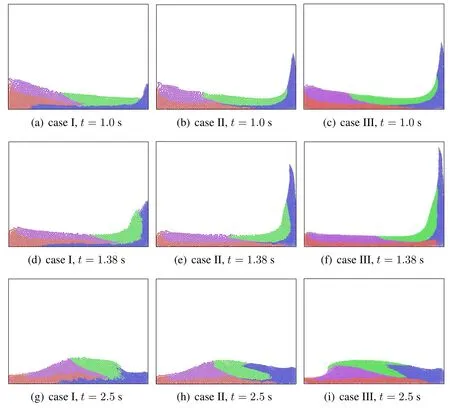
Figure 10:The profile of particles at different time
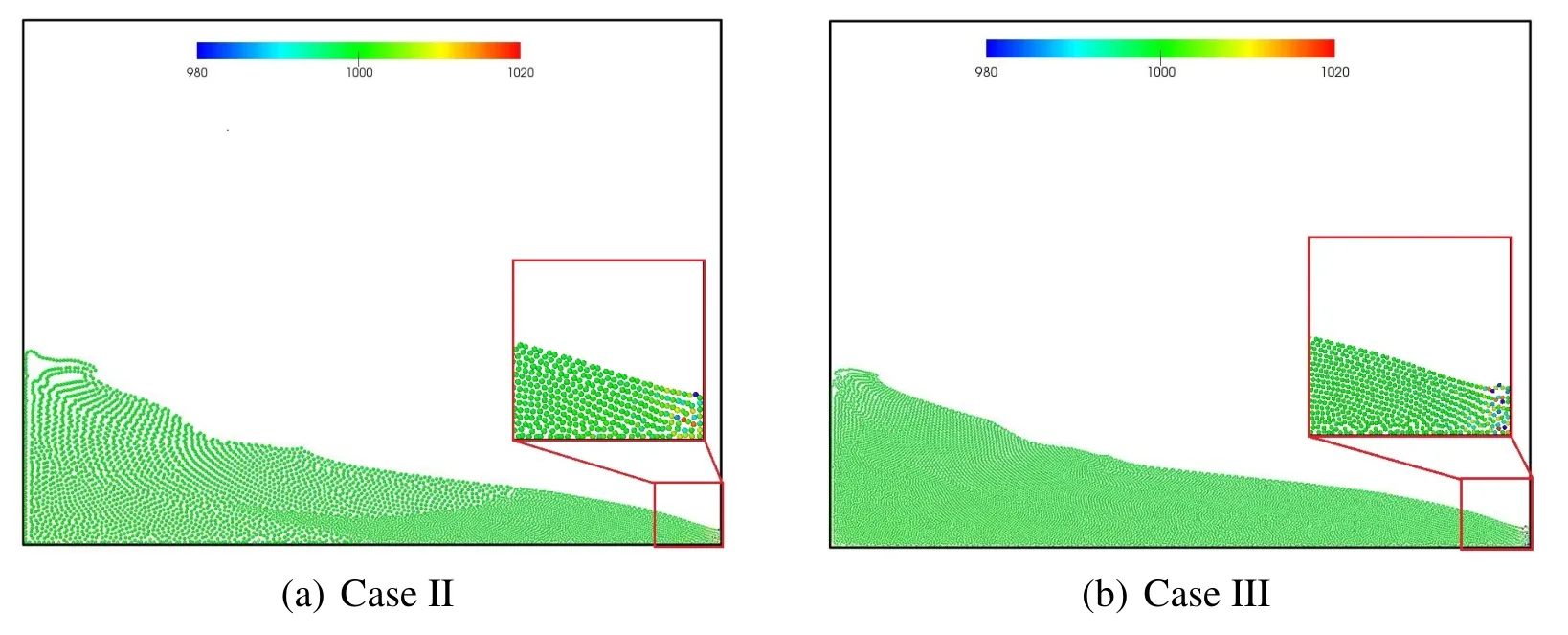
Figure 11:The density contour at different time
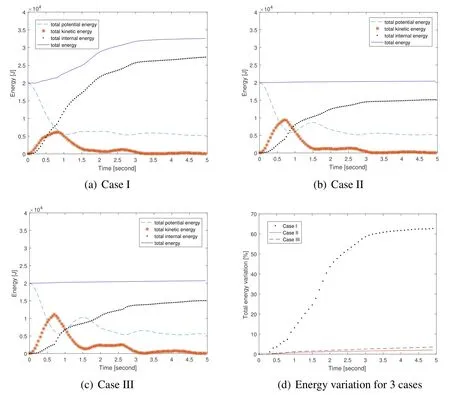
Figure 12:The total energy at different time
The total energy for three cases were compared in Fig.12.Fig.12(a)shows that the total energy of Case I increased over time,which indicates that the spurious force has a great impact on the global energy conservation.In fact,the spurious force is the unbalance force interaction between two particles with different smoothing lengths.For Case II and Case III,the total energy variation arising from the time integration is less than 4%.Therefore,the dual-support SPH formulation conserves the global energy in the absence of external force doing work.The dual-support formulation is a good alternative to varying the smoothing lengths in SPH.
8 Conclusions
In this paper,we have introduced the dual-support domain,the dual part of support domain,based on which the conventional SPH was reformulated into dual-support SPH.
We identified that the duality of influence domain and support domain in conventional SPH method.This formulation enables the conservations of momentum,angular momentum and energy when variable support domains are employed.In DS-SPH,the change of smoothing length is achieved with ease and the modified coefficients in Eq.(14) and Eq.(16) are eliminated.The implementation of DS-SPH shows that the DS-SPH can reduce the computational cost compared with traditional SPH.
Three numerical examples were presented to validate the dual-support SPH.The first numerical example showed for heat diffusion problem the energy is conserved when variable smoothing lengths are utilized.The third numerical example verified that the conservations of basic laws for DS-SPH are well preserved while the traditional SPH not.The last example showed traditional SPH is greatly affected by the variable smoothing lengths and DS-SPH can eliminate the adverse effect.
The concept of dual-support facilitates the support-variable SPH formulation.To some extent,the concept of support domain and dual-support domain is similar to Newton’s third law,considering the direct force and reaction force for paired particles.The proof of conservation is obtained easily with the aid of duality of dual-support and support domain.Therefore,the dual-support can be also applied in the SPH on solid or SPH on magnetohydrodynamics.The present method is also promising for multi-scale analysis where the models with different length scales can be bridged by using different smooth length settings.
Acknowledgement:The authors acknowledge the supports from the ERC-CoG(Computational Modeling and Design of Lithium-ion Batteries (COMBAT)),RISE-BESTOFRAC and National Science Foundation of China(51474157).
Appendix A:The duality of dual-support
LetF(i,j) be any expression depend on two pointsi,j.The duality of dual-support is that the double integral of the termF(i,j)in dual-support can be converted to the double integral of the termF(j,i)in support,as shown in Eq.(22)and Eq.(23).The key idea lies in that the termF(i,j)can be both interpreted inHiandH′j.

Proof:
Let Ω be discretized withNvoronoi tessellations(or other shape),as shown in Fig.13.
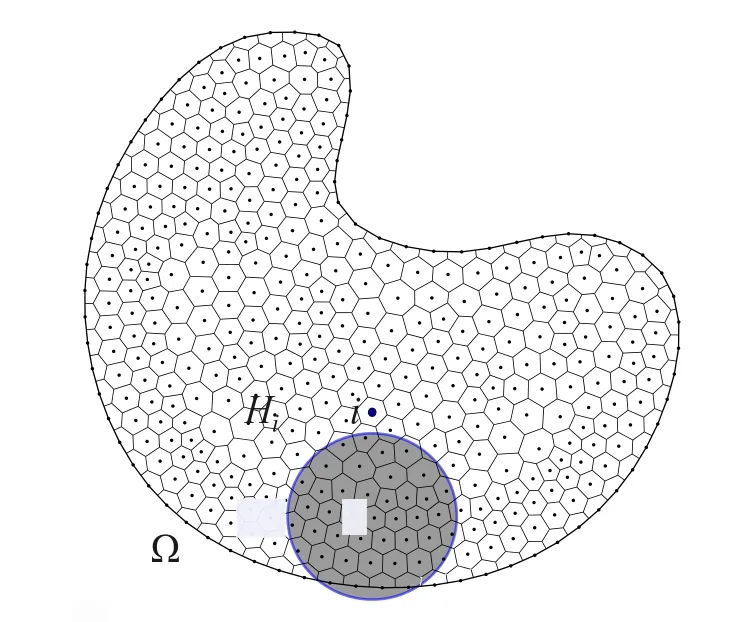
Figure 13:The discretization of domain Ω
Each polygon is denoted with an indexi ∈{1,···,N},riis the coordinate fori’s center of gravity,ΔViis the volume associated toi,HiandH′iarei’s support and dual-support,respectively.So
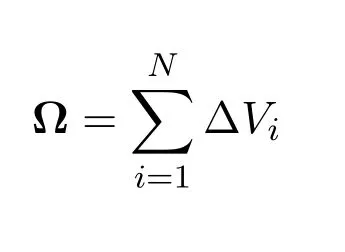
Consider the double summation ofF(i,j)on Ω.
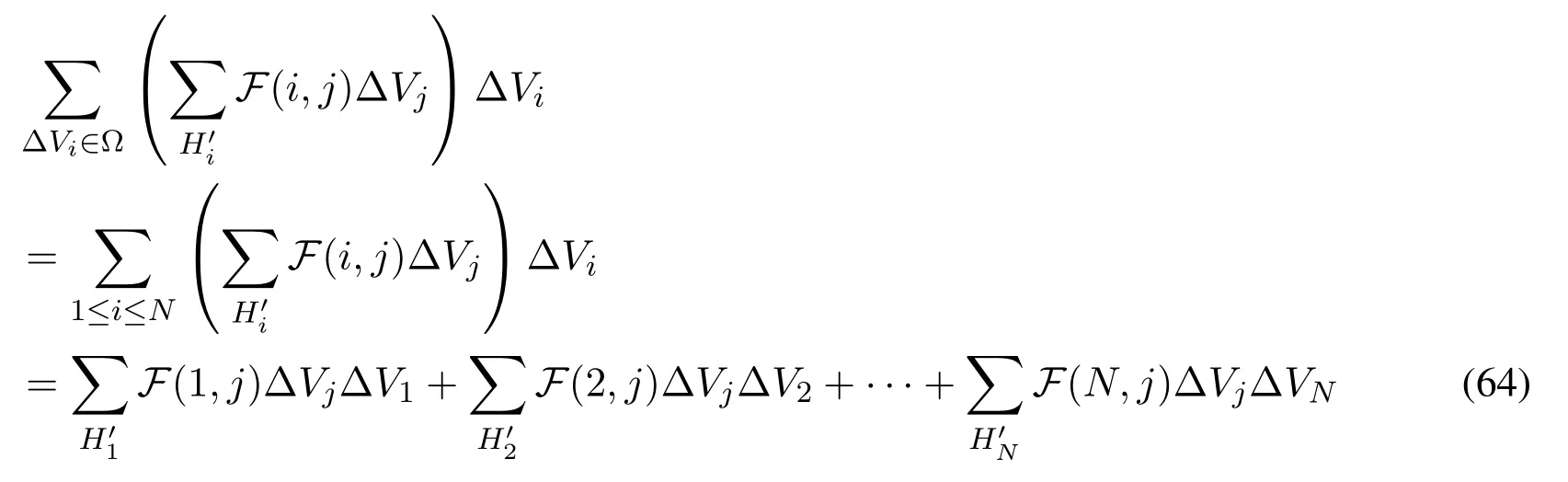
In the third step,j ∈{1,···,N}meansjbelongs to that point’s dual-support.Each termF(i,j)ΔVjΔViinH′ican be interpreted as termF(i,j)ΔViΔVjinHj.Let us sum all terms in a way based on pointj’s supportHj,wherej ∈{1,···,N}
In the second step of Eq.(65),for example,means gathering all termsj=1 in
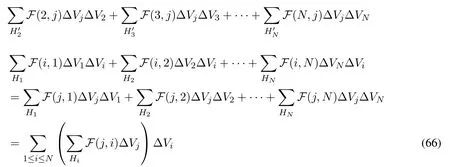
In the second step of Eq.(66),iandjis swapped.Eqs.(64)-(66)lead to
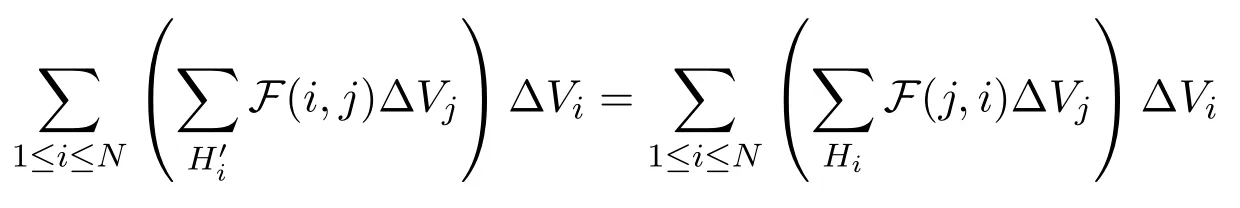
WhenN →∞so that ΔVi →0,we have
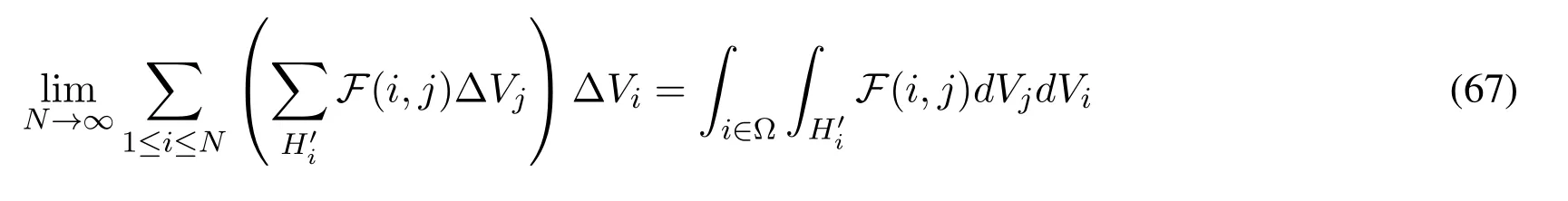
Hence the duality of dual-support in the integral form is
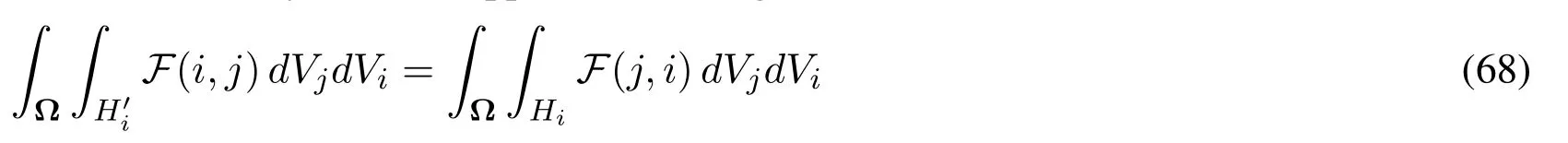
Eq.(68) means the double integral of the term in dual-support can be converted to the double integral of the term withiandjswapped in support.
Note that the domain is not necessary to be continuous,ΔVi,ΔVjcan be replaced with sparse particles with massmi,mj,respectively.So,we get
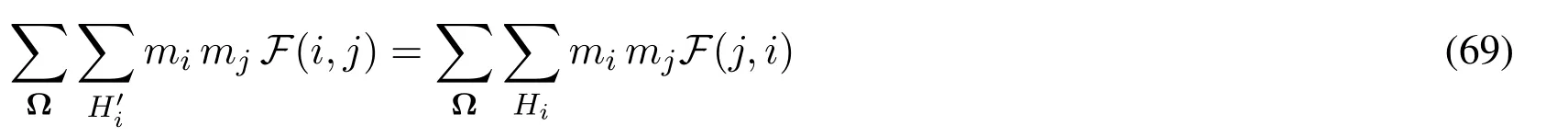
 Computer Modeling In Engineering&Sciences2019年11期
Computer Modeling In Engineering&Sciences2019年11期
- Computer Modeling In Engineering&Sciences的其它文章
- Synchronization of Robot Manipulators Actuated By Induction Motors with Velocity Estimator
- Research on Nonlinear Frequency Compression Method of Hearing Aid with Adaptive Compression Ratio
- Feature Selection with a Local Search Strategy Based on theForest Optimization Algorithm
- IDSH:An Improved Deep Su pervised Hashing Method for Image Retrieval
- Some Remarks on the Method of Fundamental Solutions for Two-Dimensional Elasticity
- A Parametric Study of Mesh Free Interpolation Based Recovery Techniques in Finite Element Elastic Analysis
