问题引领 拓展变式
张丽

勾股定理可以解决“已知直角三角形的两条边长,求第三边”问题。除此之外,在求解折叠问题时,也常会出现直角三角形及其边长的数量关系,此时可结合题意,借助相关概念及图形性质,找到或者构造出各边之间存在着某些数量关系的直角三角形,从而利用勾股定理列出方程求解。下面对这类问题进行归类整理。
一、利用折叠建立数量关系
这类问题关键是要结合已知条件,利用折叠等性质,找到或构造直角三角形,将三边用含同一个字母的代数式表示,然后利用勾股定理列出方程求解。
例1 如图1,将一个三角形纸片沿着DE折叠,使点B落在点A处,请分析图形特征,说出相关线段的数量和位置关系。
图1 图2
【解析】这是一个开放性问题,主要考查同学们对折叠性质的掌握情况,线段AD=BD,AE=BE,AB⊥DE。
变式 如图2,直角三角形纸片的两直角边的长分别为AC=6cm,BC=8cm。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
【解析】由翻折得AC=AE=6,设CD=x=DE,BE=4,BD=8-x,由勾股定理知x2+16=(8-x)2,解得x=3。
【点评】通过勾股定理建立方程是数学中常用的思想方法。先设未知数把未知的量与已知的量集中到一个直角三角形中,再通过勾股定理建立方程,然后解方程求出CD的长。
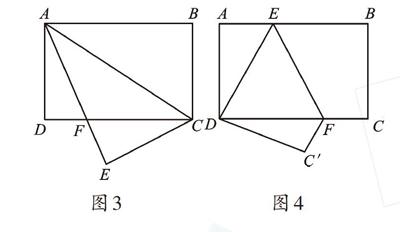
例2已知如图3,将一个长方形纸片ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F,AB=10cm,AD=8cm,求AF的长。(同学们可自己提出问题再解决)
图3 图4
【解析】这是一个开放性问题,由翻折得AB=AE=10,EC=8,设CF=x,AF=x,EF=10-x,由勾股定理知,(10-x)2+64=x2,x=8.2。当然也可以求EF等线段。
变式 在长方形纸片ABCD中,AB=10cm,AD=8cm,按图4方式折叠,使点B与点D重合,折痕为EF,求DE的长。(同学们可自己提出问题再解决)
【点评】通过勾股定理建立方程是数学中常用的思想方法。所谓方程思想,就是通过观察、分析、判断,从已知量和未知量之间的位置关系或数量关系入手,找出等量关系,运用数学符号语言将相等关系转化为方程,再通过解方程来解决问题。运用勾股定理构建方程,建立已知量与未知量之间的关系是解题的关键,同时体现了运用方程思想解题的简便快捷。
二、利用全等的性质或者等腰三角形性质建立数量关系
例3 如图5,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 。
图5 图6
【解析】根据OE=OD,可以证明△OPD≌△OGE,从而得到EG=PD,EP=DG。若设AP=x,则CG、BG可以用含x的代数式表示。在Rt△BCG中,BC的长已知,利用勾股定理列出方程求解即可。
设AP=EP=DG=x,则GE=PD=6-x,CG=8-x,BG=2+x。在Rt△BCG中,BC2+CG2=BG2,即62+(8-x)2=(x+2)2,解得x=4.8,∴AP的长为4.8。
变式 如图6,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足E。若DE=CD=1,AE=2EM,则BM的长为 。
解:连接DM,在Rt△DEM和Rt△DCM中,
[DE=DC,DM=DM,]
∴Rt△DEM≌Rt△DCM,
∴∠AMD=∠CMD。
∵AD∥BC,
∴∠DMC=∠ADM,
∴∠AMD=∠ADM,
∴AD=AM。
设EM=CM=x,则AD=AM=BC=3x,
∴BM=2x。
在Rt△ABM中,AB2+BM2=AM2,
即12+(2x)2=(3x)2,
解得x=[55]。∴BM的长为[255]。
【点评】解决这类问题的关键是首先要找到或构造出这样的一个直角三角形,利用全等、等腰三角形等性质确定其中两边的数量关系。那么,这两条边都可以用含同一個字母的代数式表示,然后利用勾股定理列出方程,求解即可。
(作者单位:江苏省太仓市第一中学)

