情境认知观照下的数学游戏化学习*

王素旦

知识不是孤立存在的，而是嵌入情境的。情境认知理论认为，知识不是个体头脑中静态的智力结构，获得知识的过程就是个体与情境交互的过程。换言之，学习具有个体与情境相联系的属性。如同工具，知识只有在应用中才可被理解和发展。

低年级学生的无意记忆占据主导地位，抗干扰能力相对较弱。操作性、互动性和参与性强的游戏化学习符合小学生的心理和认知发展特点，儿童的游戏心理与数学学习的动机机制相匹配。游戏化是学习新事物的方法，可以使思维和行动更有效。它将学习任务置于真实的情境中，能在一定程度上促进数学学习中情境与儿童身体的契合。游戏情境支持教师根据学情和知识体系结构，将教学设计与游戏形态相结合，为学习者设计并组织数学游戏化情境、基于情境的任务序列等，这有助于发挥教师的主导作用，也有利于提高学生游戏化学习的质量。

那么，如何在情境认知观照下引导学生开展数学游戏化学习呢？

一、构建知行交互多向情境的游戏场

思维的培育需要适宜的土壤，而游戏无疑是再合适不过的土壤。当情与智相融时，学生便学在玩中、乐在学中，能深刻体会到学数学、用数学的乐趣。游戏化的处理可以让学习内容变得更加生动、有趣、富有张力。以游戏为工具，挖掘情境的多向价值，激发学生的学习心向，催生更多知与行的交互，可以让学生的数学学习兴趣转变为数学学习思趣。

1.在学为中心的游戏情境中织基本知识之网。

在情境认知学习中，学生的前在知识和生活背景是有意义学习的主要基础，可以引领他们积极地进行意义的自我建构，使其始终处于学习环境的中心。因此，创设以学习者为中心的游戏情境是情境认知与学习实践的核心特征和主要任务。

游荡的零散知识容易被遗忘，这就需要学生具备将目前所学嵌入已有经验和认知结构中的能力，如此就需要教师首先有这样的意识和能力。通过游戏的浸润往往会事半功倍，有助于学生在知识间形成自组织联结。图1 呈现的就是学习苏教版一下“十几减9、8、7”时学生画的知识结构图。

（图1）

2.在意见分歧合法性中固数学技能之本。

人与人之间、班与班之间都正常地存在着差异，因为差异，所以出现不同声音和不同观点是必然的。在情境认知观照下的数学游戏化学习中，意见分歧不仅合法，而且能在共同体的互动中建立相互支持的良好环境。因此，我们需要接受这种差异，更需要基于差异发挥差异、发展差异。

【案例：苏教版五下《圆的认识》】

男女生借助教师提供的道具进行画圆比赛。女生不一会儿就画好了，但男生过了好一会儿还没画完半个，而且线条不够平滑。

师：刚才权当练手，接下来正式比赛！

女生还是非常轻松并圆满地完成了任务。

教师适时“煽风点火”：“你看这，是不是还要比试一场啊？”

“再比也是输！”一句话让现场瞬间安静下来。

“我们男生的道具有问题！”

台上的男生恍然大悟：“对！我们的绳子有弹性！”

“有弹性的绳子长度不定。”

“不公平，女生是固定位置、固定长度，而男生的虽然固定住了位置，但长度固定不了……”

一时间，七嘴八舌的声讨不绝于耳。

多变的呈现方式，使学生通过多层次体验对数学概念的核心与本质有了深刻的认知，从而能更好地抓住圆特征的关键和根本。教师引领学生经历先猜想后观察带绳小球运动轨迹形成的圆，到利用各种方法画圆，再到统一用圆规画圆并小结画圆的技术方法，再到在生活中画大圆。让学生亲历了多次画圆过程，积累了大量数学经验。接着安排男女生开展画圆比赛，男女生都信心满满，势在必得。有猫腻的游戏道具推波助澜引发了学生的思考，使他们更直观地感受到圆的本质。

3.在分布式专家互为引领中触数学思想之核。

大脑必须经过反复的、强烈的信息输入才能形成永久链接。如果新知识只从教师那里传到学生这里，从此再也不用，那这个知识就等于没学。因为神经元之间的强劲链接尚未形成，学习过的知识便如过眼云烟，因而教师应让学生在游戏、实验、辩论、研讨等多元学习过程中不断、反复取用知识。如此，就需要以“用”为手段，在多样的情境中，引导学生不断通过合法的边缘性参与直抵数学思想之核。合法的边缘性参与这一学习方式使得分布式专家在参与中变得丰富。换句话说，共同体中的每一位成员都有可能成为专家，他们都有义务与他人分享自己的专业知识，有义务促进共同体中的其他成员在某一个方面取得进步。

【案例：苏教版六下《解决问题的策略：转化》】

生2：全部转化成小数，0.5＋0.25＋0.125＋0.0625=0.9375。

生3：转化成图形（如图2）。

（图2）

小结：同学们说得真好！有的把数转化成数来解决，有的把数转化成形来解决。其实，在我们的学习和生活中， 很多时候都要用到转化的策略，你想到了哪些？接下来，我们就来进行小组间头脑风暴玩转“转化”的游戏。

A 组：二年级学习乘法时用到过转化。

B 组：我们在《数学在哪里》上见过“三角形数、正方形数”（如图3）。

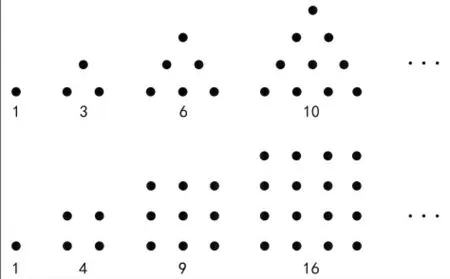
（图3）

师：古希腊毕达哥拉斯学派的“三角形数、正方形数”，把形转化成式，有意思！

从教师引着学生玩数与数的转化和数与形的转化，到学生自由创生形与数和形与式的转化，教师和学生一起玩转了“转化”策略。

二、打造意义协商多维互动的游戏实践共同体

1.以游戏构建相互依赖的系统。

情境认知理论认为，我们每个人都是实践共同体中的一员，每个人都与共同体有着不可分割的联系，通过实践，通过有意义协商，通过个体与教师或家长的互动，在游戏中更多地促进学生个体与个体之间的互动。每一次问题解决都有助于促成实践共同体的共享互动、目标理解和身份建构。在教学中，我们带领学生玩数学胜任力游戏，开展主题式数学游戏，谁有想法就听从谁的安排。在活动中，专家与新手、教师与学生、中心参与和边缘参与都是动态的，都是学习的参与者，也都有可能成为他人的“支架”。

生1：今天，我发现学校停车场边沿长了不少杂草，我觉得我们可以开展小组间PK 赛，可以比一比哪组最快清理并收集到1 千克杂草，还可以比一比最终哪组清理的杂草最重。

师（心中暗喜有意义、有意思）：很不错的提议！还有补充和完善的吗？

生2：我觉得还可以来估一估大家拔到杂草的重量，比一比谁估得准，大家也可以对每组所拔杂草的总重量进行估计。

生3：不一定只跟千克和克有关，还可以估计拔到的杂草有多长，比一比谁的眼力好。

一呼百应的行动和自发的掌声让三位学生倍感兴奋。于是，我们的“最强身体尺”和“最牛身体秤”游戏PK 赛开始了……

在游戏中，学生不断开发用数学眼光观察世界、用数学语言表达自我、用数学思维分析周边的机会与平台。正是在这样的过程中，学生的数学能力得到了更好的萌发与滋养。

2.以游戏促进多元规划与控制。

在情境认知与学习中必须给学习者提供反思的机会，使他们的关注点由原来知识的传递、个体的生长转向共同体的成长。

笔者每天都组织学生进行2 分钟“摇号点赞”游戏，每天抽取3 个学号对一节课进行相应的总结，或是全班学生对抽中的3 个学号进行评价。每当号码产生时，学生期待的眼神就亮了。从一开始不太会总结，到慢慢地讲到哪里就只会想到哪里，再到后来可以依据板书进行总结；从一开始散点评价同学的学习习惯、总结知识点一个侧面，到慢慢开始关注过程性方法、数学思想，有时还会进行知识经验和数学思想的关联，不知不觉间滋养了学生数学的情感、态度、价值观，他们的观察能力、元认知能力、合作意识、同伴和师生间的情谊都在相互鼓励中被发现了，评价也从甄选变成了促进与鼓励。

有个特别爱计较的男生，常常为了一些小事与同学争吵，三年级了还常哭鼻子。一天，在室外学习“千克”，他不允许其他人用他带来的秤，一度因为有人争抢他的秤而发脾气。可当争抢的同学一个个激动地说自己估摸着拎出的沙很接近1 千克，甚至有人当场拉着他的手跳起来以示庆祝时，可以看出他也很激动。虽然在接下来的全班争霸赛中他还是在旁边叫嚷着，不过这回叫嚷是为了让大家有序、正确地使用秤。笔者想，此刻，合作意识正在他心中扎根、萌芽。

3.以游戏催生共同体再生产循环。

整理并消化错题是提升数学学习力的一个重要途径，但要让三年级学生主动坚持并形成习惯，很多时候只是教师的一厢情愿而已。我们可以通过任务机制给出支架（如图4），让儿童的数学游戏化学习形成自我的概念地图，建构知识体系结构。在这种流程体系的游戏过程中，知识的“播种”和拥有过程从本质上来讲是双向的，学习共同体中的每个人都有可能是某方面的新手或专家，每个人都可以拥有多元的“最近发展区”。共同体内不少学生的身份在动态地发生着反转，催生着共同体的再生产循环。

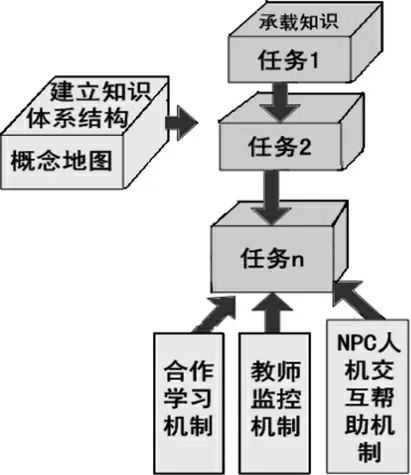
（图4）

笔者常带领学生开展“易错联盟消消乐”游戏，由每位学生准备1 道两周内出现的高频错题，组内审核并上交，每天从每个小组中抽取1道题，开展全班消错行动，根据出错频率的高低给予小组和出题者相应的积分奖励。学生在错题收集过程中真可谓“八仙过海，各显神通”，他们拼命翻看数学书、练习题中出现的易错点，有学生甚至学会了整合，从开始的翻看、收集错题逐渐演变成改编题，又从改编数据到改装出现多余信息、进行其他领域的整合等。不到三周，班里慢慢开始盛行记数学笔记，笔者私下询问学生原因，他们都不假思索地回答，这样自己知道重点，少犯错，今后出题也用得着。学生自觉自愿，自我生长。