异步电机矢量控制系统的仿真研究

李 瑾

(江西省精密驱动与控制重点实验室南昌工程学院机械与电气工程学院 江西南昌 330099)

1 前言

由于交流电机的数学模型是一个高阶、非线性、强耦合的多变量系统，使对它的转速控制不如直流电机那样方便，通过将矢量控制技术用于异步电机的转矩控制可使其调速性能够跟直流电机相媲美[1][2]。

2 异步电机的数学模型

在静止的两相Oαβ坐标系下建立异步电机数学模型如下：

(1)电压方程

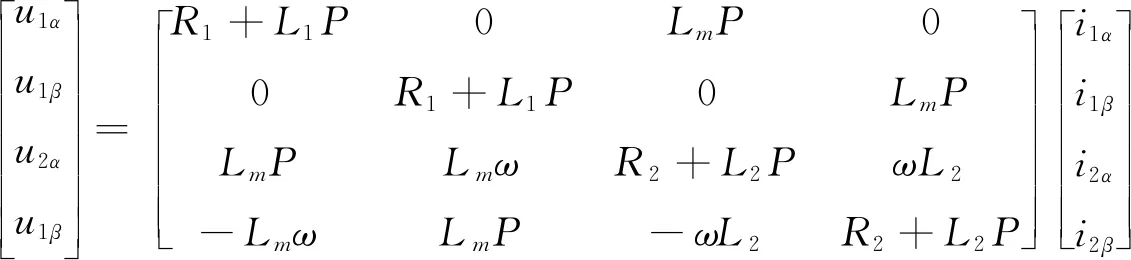
(1)

(2)磁链方程

(2)

(3) 转矩方程

Tem=npLm(i2αi1β-i1αi2β)

(3)

以上三式中，下标中的1对应定子侧、2对应转子侧的物理量，np为极对数，Lm为定转子绕组的互感，ω为电机角速度。

3 矢量控制策略

本文采用定子磁链定向矢量控制，即将旋转坐标的M轴定向于定子磁链Ψ1方向上，则定子磁通Ф1的T轴分量等于零。如果保持Ф1恒定，那么转矩正比于T轴电流，这样转矩就直接等于两个标量之积，能更好地实现对转矩的控制[3]。另外采用定子磁链定向可使定子磁链观测过程与转子参数无关从而能够简化控制系统的结构。系统的矢量图如图1所示，其中MT坐标系以同步转速ω1旋转，dq坐标系以转子转速ω旋转，α轴为坐标系旋转的参考轴，则有θs=θ1-θ2=(ω1-ω)t为转差角。

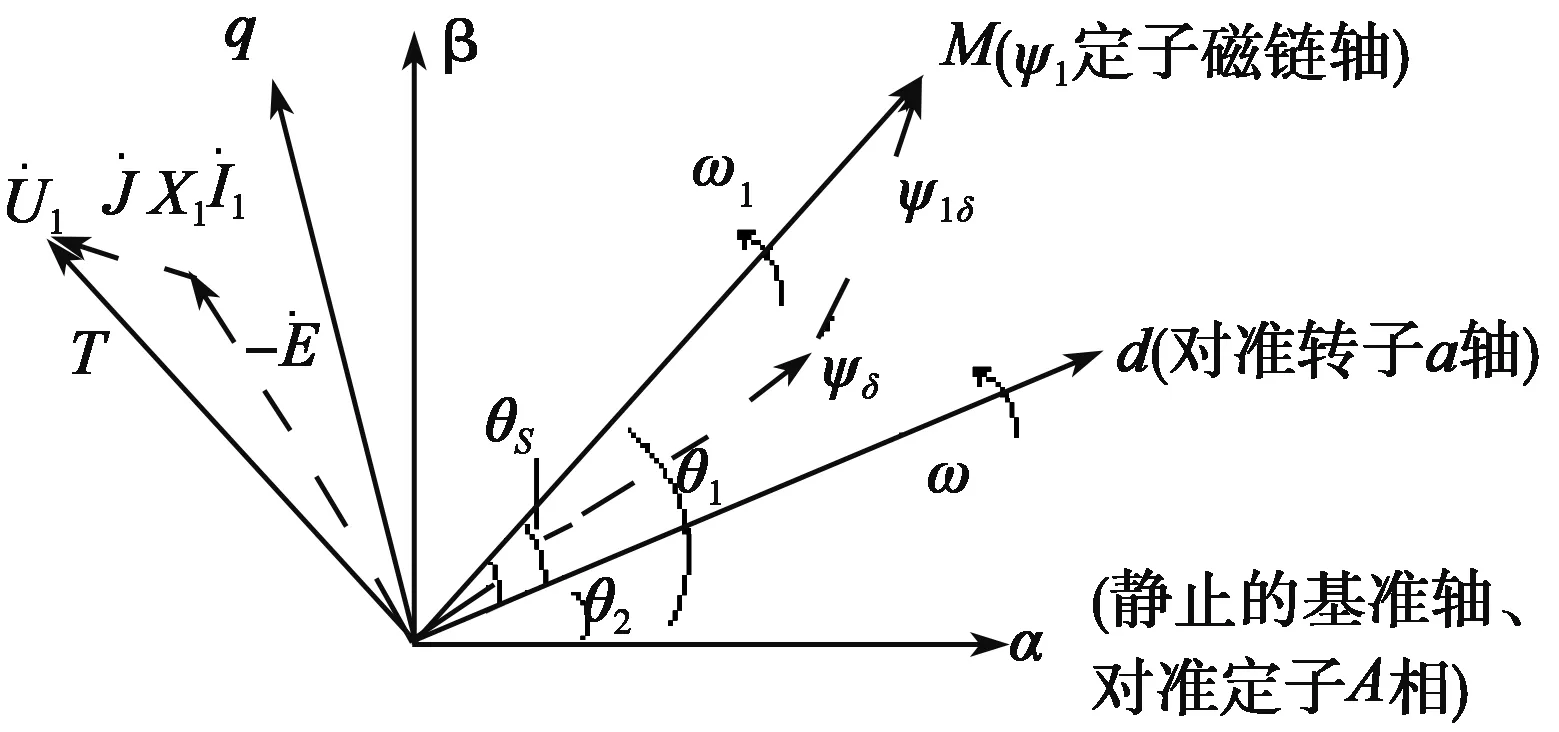
图1 矢量图

要实现定子磁链定向，需要定子磁链矢量的准确值，这里采用由检测出的定子电压和电流来计算定子磁链的U-I模型，图2是U-I模型的结构框图。

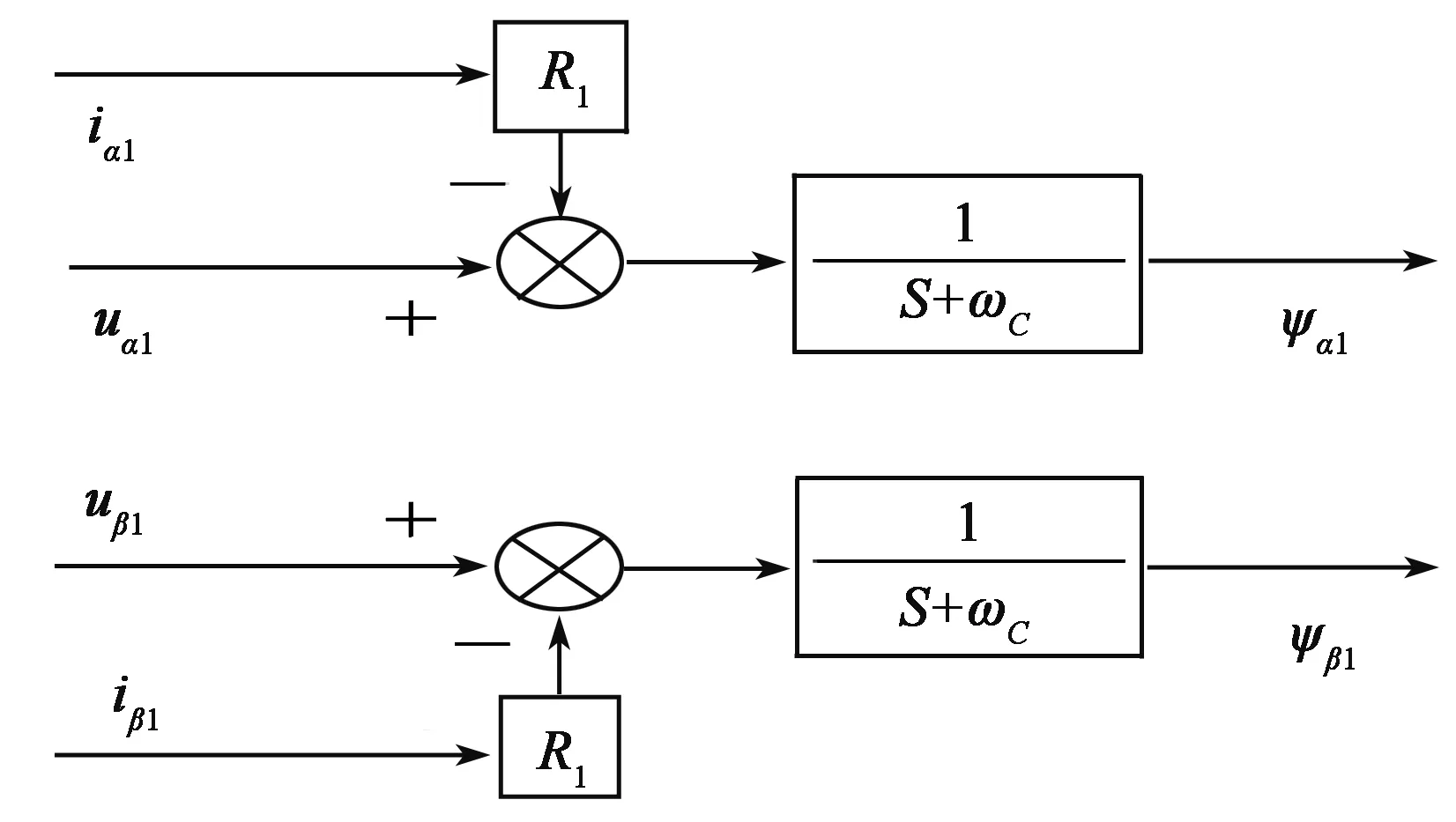
图2 定子磁链的U-I模型结构框图

4 坐标变换公式

(1)2/3变换

根据磁动势等效，(4)式是由两相Odq坐标系向三相Oabc坐标系(a轴与d轴重合)变换的公式(Odq坐标系与Oabc坐标系都以ωr速度旋转，且三相绕组Y接法，无零线)。由图1可得由以ωr速度旋转的odq向静止的oαβ坐标系及由以同步转速ω1旋转的OMT坐标系向静止的oαβ坐标系转换的公式分别如(5)(6)式所示：

(4)

(5)

(6)

由以上两式有：

(7)

将(7)式代入(4)式有

(8)

(8)式即是由同步旋转的OMT坐标系变换到以ωr速度旋转的oabc坐标系的2/3变换(其中含旋转变换)公式。

(2)3/2变换

由(4)式和(7)式可得：

(9)

(10)

由(9)，(10)两式可得由oabc坐标系变换到同步旋转的OMT坐标系的3/2变换(其中含旋转变换)公式。

(11)

5 系统仿真实验

5.1 仿真框图

运用MATLAB软件对调速系统矢量变换部分进行仿真，得出仿真模型。

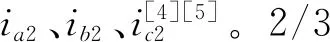
5.2 仿真波形

在仿真图的基础上对整个矢量控制系统进行建模仿真，电机参数设置如下：额定功率750W，额定电压380V，额定转速1420r/min，4极，功率因数0.86，效率84%。

初始给定转速为1400r/min，t=0.2s时给定转速值变为1000r/min，仿真得到的转速波形如图3所示。

图3 在0.2s转速给定1000r/min时的转速波形

从图中可看出，当电机给定转速值发生突变时，响应非常迅速，动态调整时间大约只有0.01s。

给定转速1400r/min，电机空载起动，在0.2s时突加负载5N·m，得到的转速和转矩波形分别如图4和图5所示。

从图4和图5可见当突加负载时，电机的转速和转矩都能很快响应，t=0.2s时转速经过短暂的动态调整之后迅速回复到给定值1400r/min，在t=0.2s时转矩迅速上升，然后很快就稳定在负载转矩值5N·m，响应非常迅速，说明系统的抗扰性能较强。

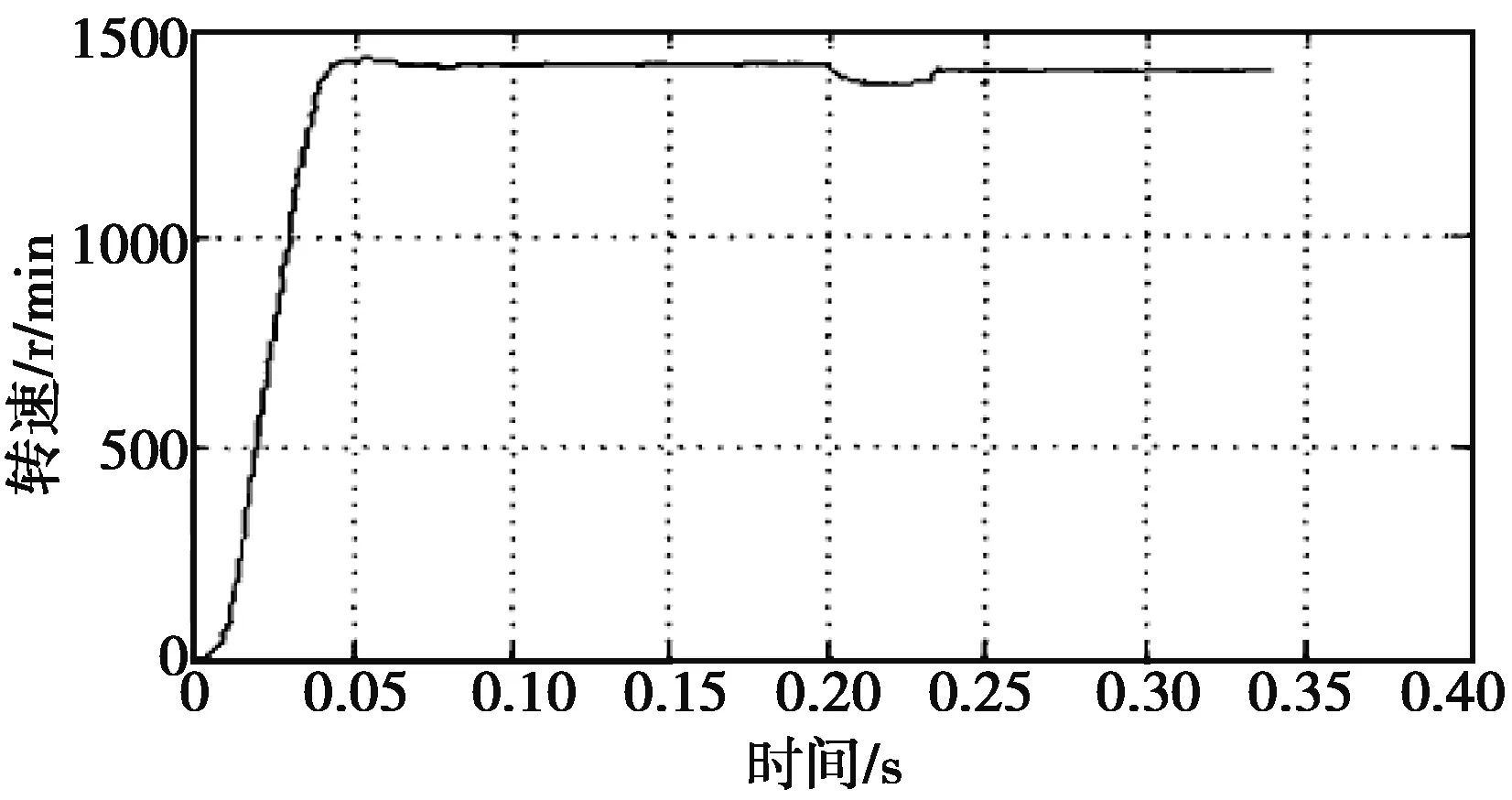
图4 在0.2s突加负载时的转速波形

图5 在0.2s突加负载时的转矩波形

6 结论

本文分析了矢量控制原理，建立了采用定子磁链定向控制的异步电机矢量控制系统，对该系统进行仿真实验的结果表明，采用本文所述的控制策略可使异步电机获得完全能够跟直流电机相媲美的调速性能。