基于地震易损性的连续梁桥减隔震方案研究

周 波，魏鲡鋆，宋新龙

(中铁西北科学研究院有限公司，甘肃 兰州 730000)

0 引言

我国地处亚欧板块与太平洋板块之间，地壳运动活跃、地震频发[1]。21世纪以来发生的汶川地震、玉树地震等多次强震造成了大量桥梁毁坏甚至倒塌，给国家带来了巨大经济损失。高速铁路桥梁作为生命线工程，其在地震作用下的安全性是高速铁路安全运营的重要保障[2]。

连续梁桥以其刚度大、变形小及动力性能好等特点在高速铁路线上广泛采用[3]。地震作用下连续梁桥的震害主要表现为支座失效和桥墩损伤等破坏形式。高烈度区高速铁路桥梁一般需通过减隔震设计改善结构抗震性能，使结构满足抗震设防要求。王传坤等[4]考虑轨道约束及墩柱弹塑性，采用时程分析法对摩擦摆支座最优隔震参数进行分析；温留汉·黑沙等[5]针对高烈度区高速铁路减隔震装置难以满足设防要求的问题，提出功能分离减隔震理念，并通过振动台试验对分离型减隔震系统进行研究；李健宁等[6]采用粘滞阻尼器与双曲面球型隔震支座配合使用的方案，对某高烈度大跨连续梁桥进行了减隔震设计，并对粘滞阻尼器和双曲面球型支座的工作机理进行了探讨；冯亚成[7]对某高速铁路连续梁桥4种减隔震方案进行对比分析发现，在结构中同一部位的减隔震措施并非愈多愈好，还应使减隔震措施之间保证协同工作，在减隔震设计中需慎重考虑。

本文结合高速铁路桥梁的特点，在既有研究的基础上选用4种减隔震设计方案对算例桥梁进行地震易损性对比研究，为高速铁路桥梁减隔震优化设计提供必要参考。

1 工程概况及减隔震方案

1.1 桥梁概况和有限元建模

本文以一座孔跨布置形式为(48+80+48)m的高速铁路连续梁为工程背景，结构主要尺寸如图1所示。该桥主梁采用C55混凝土，中墩采用C50混凝土，边墩采用C40混凝土。桥址位于Ⅷ地震区，场地类别为Ⅱ类，设计地震加速度为0.3 g，场地特征周期为0.45 s。

图1 连续梁立面布置Fig.1 Layout of continuous beam elevation

基于有限元软件MIDAS/Civil建立全桥非线性有限元模型。模型主梁采用线性梁单元模拟；桥墩采用非线性纤维梁柱单元模拟，其中，桥墩主筋运用双折线模型，核心混凝土运用Kent-Park模型。梁、墩与支座采用主从约束，支座和阻尼器采用一般连接模拟。有限元模型如图2所示。

图2 有限元模型Fig.2 Finite element model

1.2 减隔震方案

高烈度区高速铁路桥梁通常采用减隔震设计以满足结构抗震设防要求。高铁桥梁多采用液体粘滞阻尼器、双曲面球型隔震支座等装置进行减隔震设计。然而，减隔震装置高昂的造价给利益相关者带来巨大的经济压力。为使桥梁满足抗震性能要求的同时兼备经济性，本文选取4种方案进行对比分析，具体布置方案见表1。

表1 减隔震措施布置方案Table 1 Arrangement schemes of seismic mitigation and isolation measures

表1中普通固定支座的水平承载力按竖向承载力的20%考虑[8]。减隔震支座选用KZQZ型双曲面球型隔震支座，其中，中墩支座竖向承载力为35 000 kN，等效曲率半径为5.0 m；边墩支座竖向承载力为7 000 kN，等效曲率半径为3.0 m；隔震支座设计位移为150 mm，屈服位移取为2.5 mm，支座摩擦因数取为0.03。隔震支座滞回模型选用双直线简化模型[9-10]，普通支座选用盆式支座，阻尼器选用液体黏滞阻尼器。为兼顾现场安装方便并取得较好的减震性能，5#，8#墩顶各设2个FVD-1 000 kN型，6#，7#墩顶各设4个FVD-2 500 kN型。有限元模拟时，双曲面球型隔震支座采用双折线模型，阻尼器采用Maxwell模型。

2 地震动选取

从美国太平洋地震工程研究中心(PEER Center)调用与该桥场地条件相近的14条地震记录。将峰值加速度(PGA)作为地震动强度指标，采用等步长分析方法以0.05 g为步长进行调幅，逐一输入有限元模型进行计算分析。选取地震记录信息见表2。

3 地震易损性分析

3.1 损伤指标

运用X-TRACT程序对墩底进行弯矩-曲率分析，得到初始屈服曲率、等效屈服曲率、混凝土压应变为0.004时的曲率和极限曲率。由塑性铰公式求得对应位移作为桥墩损伤状态指标。

因缺乏支座的试验实测数据，本文参考文献[11-12]以支座容许位移、1.5倍容许位移、2.0倍容许位移、0.5倍球面直径为隔震支座和普通活动支座轻微、中等、严重及完全损伤的性能指标；普通固定支座取10，15，20，50 mm 4种状态的性能指标。

桥墩和支座各损伤状态位移延性比μi定义为：

(1)

式中：Δi为第i个损伤状态的临界位移，mm；Δy为纵筋首次屈服位移，mm。

表2 地震动记录Table 2 Seismic motion records

对算例桥梁桥墩、支座位移延性比进行计算，得到损伤状态划分指标见表3。

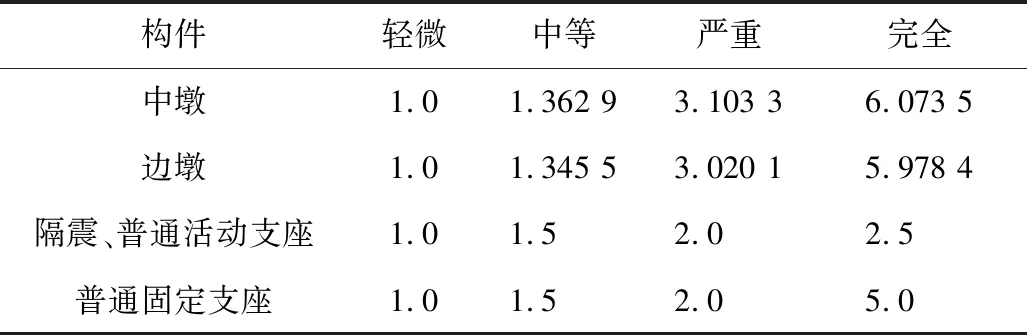
表3 损伤状态指标Table 3 Indexes of damage status

3.2 易损性分析

相较于传统确定性分析方法，地震易损性分析法可以更全面地评价桥梁在寿命期内的抗震性能。大量震害资料表明，主梁在地震中损伤的概率通常较小，主要损伤构件为支座和桥墩，且支座遭遇震害损伤的概率较大，因此仅用桥墩地震易损性代替全桥系统地震易损性会引起较大误差。

本文在计算中将支座与桥墩采用串联方式，即假定任意构件达到极限状态就认为桥梁系统达到了极限状态。桥梁系统失效概率计算公式为[13-14]：

(2)

式中：Psys为系统达指定损伤状态的超越概率；P(Fi)为第i个构件达指定损伤状态的超越概率。

在此采用幂运算定律，假设在地震作用下结构地震需求与地震强度符合对数线性关系[15-16]，建立PGA与支座、桥墩位移延性比的概率地震需求函数关系，见表4。

利用式(3)求得支座和桥墩构件地震易损性曲线[17]，再通过桥梁系统失效概率计算方法得到4种方案下的该桥系统地震易损性曲线，如图3所示。

(3)

式中：μd，μc分别为结构需求和结构能力；βc，βd为结构能力和地震需求对数标准差。

根据图3中4种破坏状态超越概率可知，桥梁系统易损性概率由各工况下界控制，下文中主要对4种方案的系统易损性下界展开分析。

由图3可知：1)地震动强度相同时，基于一次一阶矩方法的桥梁系统易损性下界较上界概率有所增大，表明仅考虑单个构件代替全桥易损性会显著低估结构的破坏概率；2)仅采用桥墩延性设计(方案1)时，在设计地震动强度下，桥梁系统发生轻微、中等破坏的概率趋近100%，显然不满足规范抗震设防要求，必须通过减隔震设计改善结构抗震性能；3)方案3和方案4发生轻微、中等破坏的概率较为接近，但方案4由于在边墩设置了减隔震支座，因此发生严重破坏和完全破坏的概率明显降低；4)全桥采用隔震支座与粘滞阻尼器配合使用(方案2)时，结构地震易损性最低，为本文4种方案中的最优方案。

表4 各方案下不同构件地震需求响应回归分析Table 4 Regression analysis on seismic demand response of different components under each scheme

图3 桥梁系统易损性曲线Fig.3 Vulnerability curves of bridge system

根据《规范》[18]，结构在抗震设计中须满足“小震不坏、中震可修、大震不倒”的原则，即在小震作用下不发生损伤或者轻微破坏，在中等强度地震下可发生轻微破坏，且易于检查修复，在强震作用下可发生较大破坏但不至倒塌。本文基于损伤超越概率对规范中的定性描述进行量化，在此假定结构在某一损伤状态的系统易损性大于50%时即会发生该种损伤。该桥小震、中震和大震峰值加速度分别为0.1，0.3，0.57 g。基于上述原则可以发现：1)方案1远不满足规范要求；2)方案2在小震和中震下发生轻微破坏的概率分别为0%和28.6%，在大震下发生严重破坏和完全倒塌的概率为16.6%和1.5%，由此可见该方案设计过于保守，尤其昂贵的粘滞阻尼器会造成结构初始造价的显著提高；3)方案3和方案4在小震和中震下均满足要求，但在大震作用下，方案3和方案4发生完全破坏的概率分别为78.4%和43.7%。

综上分析，方案2与方案4均能满足结构抗震设防要求，但方案2过于保守的抗震设计造成了结构经济性较低。综合结构力学性能和经济性，方案4为本文所选方案中的最优方案，该方案在地震动较小时主要通过隔震支座进行耗能，当地震动强度逐渐增大时，边墩上设置的粘滞阻尼器充分限位并耗能，使结构抗震性能得到显著改善。

4 结论

1)全桥采用粘滞阻尼器和双曲面球型隔震支座配合使用时，通过阻尼器的限位、耗能和球型支座摩擦耗能，使地震能量充分耗散，有效保护了桥墩构件，显著提高了结构抗震性能。

2)全桥配置双曲面球型支座且仅在位移响应较大的边墩配置粘滞阻尼器，能使结构满足抗震设防要求的同时获得较好的经济性。