城市综合管廊燃气舱室输气管道泄漏扩散规律研究*

邓小娇，姚安林,2，徐涛龙，蒋宏业

(1.西南石油大学 石油与天然气工程学院，四川 成都 610500; 2.油气消防四川省重点实验室，四川 成都 610500)

0 引言

综合管廊指建于城市地下用于容纳城市工程管线的构筑物及附属设施。为了改善拉链马路的现状，高效利用城市地下空间，便于后期对城市各类生活用管道的集中管理与维护，综合管廊的建设将成为未来的重点基础设施[1]。但管舱内天然气管道一旦发生泄漏，极有可能发生严重的燃烧爆炸事故，造成巨大的经济损失和人身伤害事故[2]，因此有必要对管廊狭长空间内天然气管道的泄漏扩散进行模拟，以便预测泄漏点位置和爆炸危险区域。

胡敏华[3]通过模型实验证明在管廊舱室内的扩散是二维的；方自虎等[4]指出距离泄漏口一定距离后，甲烷浓度的变化与泄漏口的开口方向无关；Chen[5]提出Standardk-ε模型，天然气在狭长空间的泄漏扩散更接近实验结果，并且结果满足工程精度要求；赵然[6]在进行泄漏的有限元模拟时并未加入事故通风的影响;林圣剑[7]对入廊燃气独立舱室内的通风系统进行模拟研究，得出换气次数越高，有效时间越好，舱室内所形成的爆炸空间更小，但并未针对不同管输压力作详细分析。

目前大部分学者对管廊的研究工作大多将真实管廊模型按比例进行缩减[8]，无法体现管廊长高比接近100∶1的特点，本文基于计算流体动力学理论，采用通用CFD软件FLUENT进行数值模拟[9-11]，按照管廊的真实几何参数建立综合管廊内输气管道泄漏扩散模型，研究了天然气泄漏的扩散过程、特点以及管输压力、通风速度等关键因素对可燃气体爆炸危险区域的影响规律，从而进一步探讨可燃气体报警器的报警时间和关闭阀门后的解除报警时间。

1 气体扩散模型

对于气体扩散半经验模型，国外学者提出高斯模型[12]、箱模型[13]、Sutton模型[14]等，随后国内学者又对这些半经验模型进行了改进[15-16]。气体扩散的理论模型仍被广泛应用，但上述模型的准确性会受到模型假设和气体扩散条件的影响[17]。

1.1 高斯模型

高斯模型(Gaussian Model)分为高斯烟团模型(Gaussian Puff Model)和高斯烟羽模型(Gaussian Plume Model )。管道上小孔或缝隙持续漏气时，因发生连续泄漏，即泄漏排放时间与扩散时间相当，泄漏时间比较长，故选用高斯烟羽模型。

由于高斯模型未考虑气体自身重力的作用，所以只适用于描述密度不大于空气的气体泄漏扩散。模拟的精度虽较差，但对于大规模连续性或短时间瞬时泄漏均可模拟。

1.2 箱模型

1970年，Uan[18]在重气气云实验中发现重气下沉的规律，模拟重气气云的扩散状况时提出箱模型的概念。

该模型假设扩散区域内的浓度场、温度场等在下风向的任一横截面上均满足均匀分布(又称矩形分布)。这类模型在考虑重力的基础上，只能描述气云的平均状态，不能描述细节状态。

1.3 Sutton模型

英国学者萨顿(O.G.Sutton)从泰勒公式中的拉格朗日相关系数的具体形式求得扩散参数。再将其代入高斯模型得到Sutton模型。该模型是在高斯模式和泰勒公式的基础上发展的一种用气象参数进行扩散估算的经验公式，适用于密度不大于空气的气体，大规模长时间泄漏扩散的模拟，计算量小，对模拟湍流效果好，但误差较大。

2 气体泄漏扩散物理模型

由于研究对象主要关注天然气在管廊长度方向的浓度分布和报警时间，此外，建立三维模型对计算机配置要求过高，本文假设天然气沿管廊宽度方向的浓度梯度较小，采用ICEM软件建立沿长度(X轴)和高度(Y轴)方向的二维天然气扩散模型。按照国家标准[19-20]设计管舱空间的几何尺寸，选取2.4 m作为管廊高度，防火区间200 m作为计算域长度。本文主要针对中压、次高压管道，因为这类管道在管舱的相对密闭空间泄漏后，气体扩散范围更广，潜在风险更大。为了便于计算将泄漏孔处理为20 mm孔径的圆形孔口，如图1所示。

图1 天然气管舱几何模型Fig.1 Geometric model of natural gas pipeline cabin

根据国家标准[21]，可燃气体处于封闭或局部通风不良的半敞开厂房内，每隔15 m设置1台探测器，且探测器距其所覆盖范围内的任意释放源不宜大于7.5 m。因此，本文将可燃气体报警控制器对称布置在泄漏源两侧，坐标点依次为x=-22.5,-7.5,7.5,22.5 m。

2.1 模型简化

为了简化计算过程，根据管舱内的实际布置情况，在满足工程精度的条件下可忽略一些次要因素，具体假设如下[22]：

1)天然气泄漏口处的泄漏压力恒定。

2)忽略空气粘性的影响。

3)假定泄漏天然气全为甲烷，且是理想气体，气体之间不发生化学反应。

4)泄漏过程中，温度恒定且与外界无热量交换。

2.2 网格划分

采用结构化网格进行划分，但因泄漏孔径相较于防火区间长度200 m的量级差异接近104，故必须对泄漏孔及进出风口进行局部网格加密，网格数共计41 598个，网格质量约为0.7。

2.3 模型参数及边界条件

Fluent计算基于压力求解器，采用Standardk-ε模型模拟湍流流动、组分输运模型(Species Transport)模拟天然气在大气中的泄漏扩散过程。

泄漏孔口喷射出的高速流体视为可压缩的流体，故采用质量流量入口，流量值按照侯庆民[23]所提的公式计算。进风口采用速度入口，正常通风换气次数(6次/h)和事故通风速度(12次/h)换算成速度分别为1.92，3.85 m/s。管廊防火墙两端和排风口均采用压力出口，管廊壁面采用无滑移的恒温壁面。

3 数值模拟及结果分析

3.1 报警响应时间

地下综合管廊中天然气报警浓度设定值不应大于其爆炸下限值(体积分数)的20%，换算成质量分数为0.6%。为了考察最长的报警响应时间，将泄漏源设在2个可燃气体报警控制器的中点。

在2.1节模型简化的基础上，将外部大气压设为1个标准大气压，环境温度为300 K，小孔泄漏孔径为20 mm，模拟正常通风风速(1.92 m/s)、管输压力为200，400,800 kPa时的报警时间，报警时刻t的数值及相应的浓度分布如图2所示。3种管输压力下最先响应的报警器位置均是x=7.5 m处，即顺风侧方向距离泄漏源最近的可燃气体报警控制器，进而推断报警器正常响应时，泄漏源坐标位于报警器的逆风侧7.5 m范围内。在不同管输压力对应的报警时刻，逆风侧的扩散距离与管输压力成正比，当p=800 kPa时逆风侧扩散距离最远。由此可知，顺风侧比逆风侧扩散速度快，天然气在管舱内扩散后浓度并不呈对称分布。

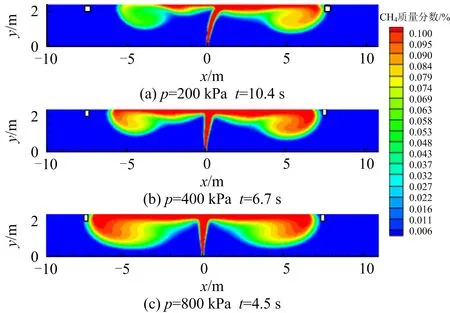
图2 不同管输压力报警时刻浓度分布Fig.2 Geometric model of natural gas pipeline cabin

不同管输压力的报警响应位置及报警时间如图3所示，随着压力从200 kPa增加到800 kPa，相同位置报警器的报警时间呈倍数减小且最大幅值位于x=-22.5 m。说明报警时间和管输压力成反比，随着管压的增加报警时间逐渐减小。

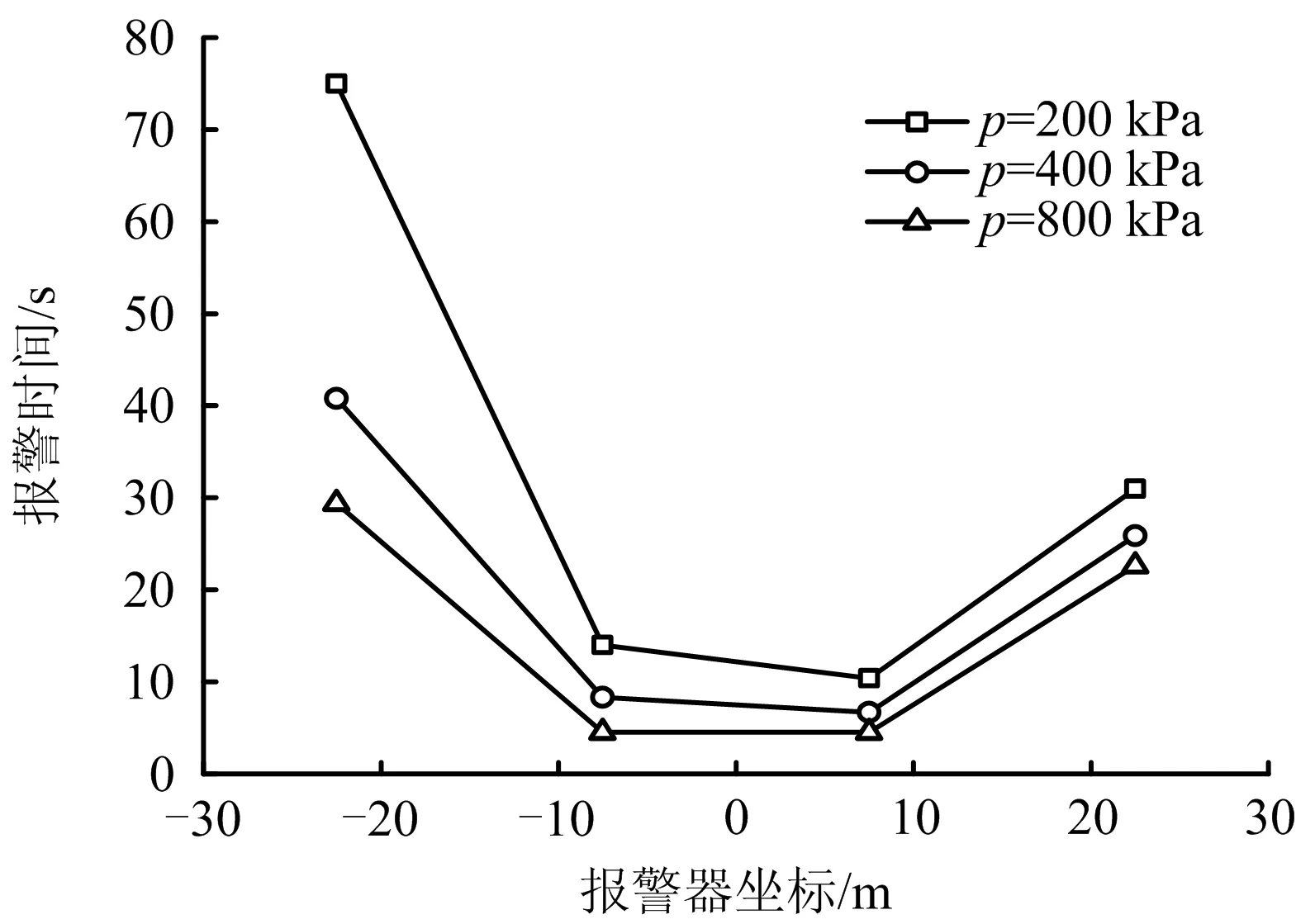
图3 不同管输压力的报警响应位置及报警时间Fig.3 Alarm response position and alarm time under different pipeline transportation pressures

报警响应曲线是指报警时间t与报警器坐标x的关系，由数据拟合得到抛物线型函数关系式：p=200 kPa时，t=0.078x2-0.978x+13.348；p=400 kPa时，t=0.046x2-0.107x+4.915；p=800 kPa时，t=0.045x2-0.151x+3.216。

若距离泄漏源最近的报警器因故障而失效，则报警时间随报警器坐标的递增呈抛物线型增长，报警时间的延长将给现场救援队伍对泄漏源和泄漏时间的判断增加难度。因此，实际工程中应定期检修报警器以尽可能降低其失效概率。

3.2 扩散实时位置分析

为了考察报警装置响应后的天然气扩散情况，将进风口风速取事故通风速度(3.85 m/s)，其余条件与3.1节一致。如图4所示，在3种不同管输压力泄漏后，天然气均能在200 s内扩散至1个防火墙距离，且顺风侧的扩散趋势比逆风侧平缓。3种工况的扩散距离到达极值后均不再增加，因为逆风侧到达泄漏扩散边界，而顺风侧也已经扩散到管廊计算域的右端。天然气的扩散速度随着管输压力的增大而增大，从而天然气到达管廊两端边界的时间与管输压力呈负相关。

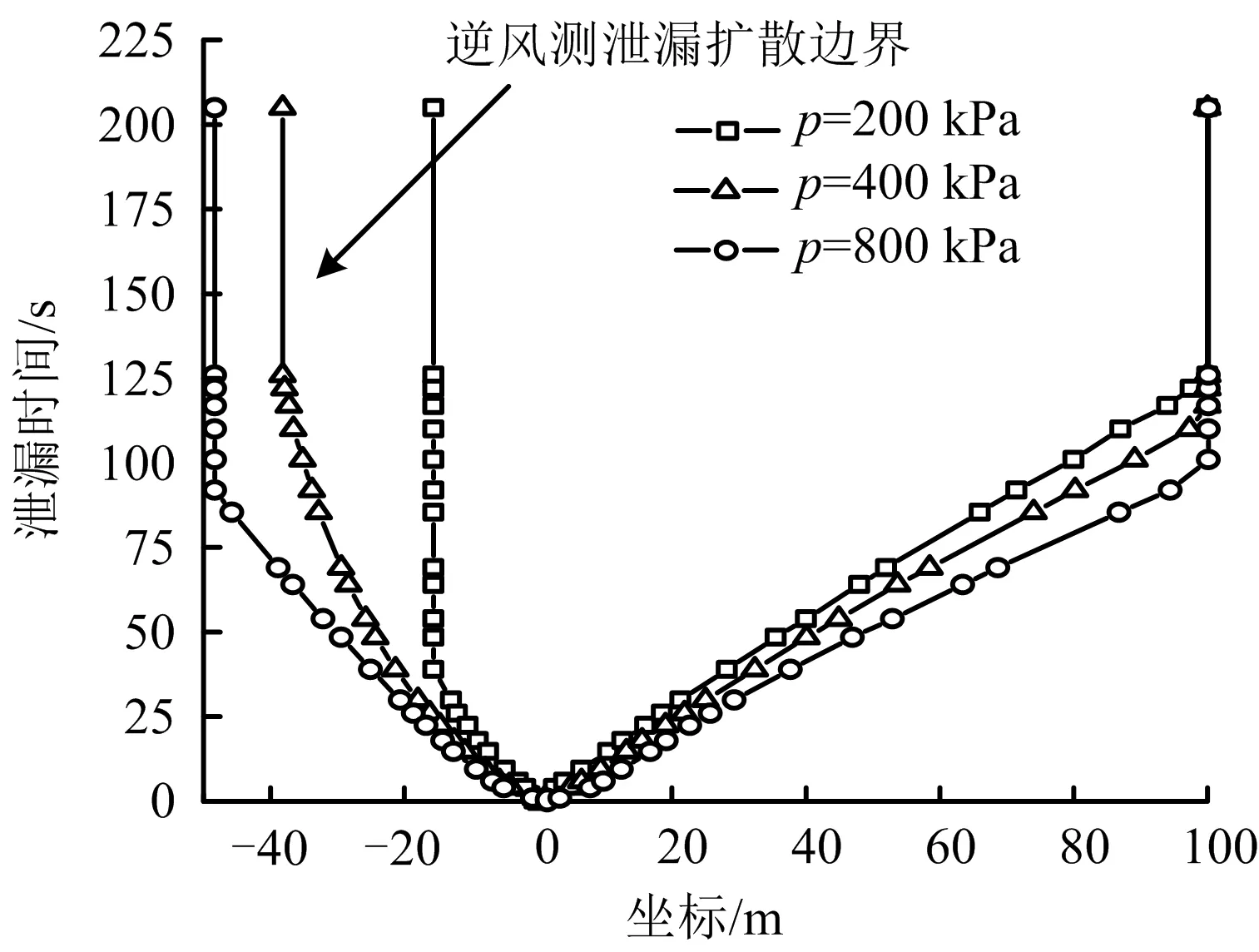
图4 不同管输压力下随着泄漏时间变化的扩散位置Fig.4 Diffusion location changing with leakage time under different pipeline transportation pressures

天然气泄漏扩散至逆风侧边界局部图如图5所示，在进风口风速的吹扫作用下，当管输压力为200，400和800 kPa时，向逆风侧扩散的最远端分别在x=-15.6，-38.2，-50.3 m处。研究发现，天然气在管舱内发生泄漏后，在进风口风速和管输压力的共同影响下天然气的初始动量不同，天然气朝逆风侧扩散时自身动量逐渐减小，导致逆风侧存在泄漏扩散边界且位置不同。此外，天然气因自身密度小产生的浮力起主导作用，逐渐向管舱上方空间聚集。

图5 不同管输压力下逆风侧的泄漏扩散边界Fig.5 Leakage diffusion boundary at upwind side under different pipeline transportation pressures

3.3 天然气爆炸极限浓度区移动速度

由于管廊兼有报警系统和通风系统，报警器一旦响应，通风装置将会加大进风口风速，爆炸危险区域会在风速动态变换的影响下随泄漏时间的推移而移动。因此，合理的预测天然气爆炸极限移动速度将为现场救援队伍判断爆炸危险区域起到一定的指导作用，最大程度地降低火源在天然气爆炸范围内出现的可能性。

将进风口风速取事故通风速度(3.85 m/s)，其余条件与3.1节一致，天然气泄漏扩散后的浓度分布如图6所示。t=18 s时，管输压力为200，400，800 kPa的爆炸下限到达位置分别为：x=10.1，15.5，18 m。由此可知，天然气爆炸极限移动速度与管输压力成正比。而距离泄漏口两侧15 m内的爆炸范围与管输压力成反比，管输压力越高，初始喷射速度越快，故当p=800 kPa时天然气由泄漏口快速向管舱内喷射，该区域内大部分天然气浓度超过爆炸上限，导致爆炸范围的减小。

图6 t=18 s时不同管输压力的天然气扩散质量分数Fig.6 Mass fraction of natural gas diffusion under different pipeline transportation pressures at t=18 s

用天然气最高爆炸极限移动速度来反映不同管输压力下处于爆炸上限的气体移动速度，如图7所示，天然气爆炸极限移动速度的初始值随管输压力的增大而增大，p=200 kPa时，在t=10 s内快速上升至0.7 m/s；p=400 kPa与p=800 kPa的移动速度则是先上升后快速下降，最终在t=125 s后达到相同的移动速度0.75 m/s。

图7 不同管输压力时最高爆炸极限移动速度Fig.7 Moving velocity of maximum explosion limit under different pipeline transportation pressures

用天然气最低爆炸极限移动速度来反映不同管输压力下处于爆炸下限的气体移动速度，如图8所示，在t=20 s内，天然气爆炸极限移动速度的变化最剧烈，之后100 s内趋于平缓，最终在t=120 s后达到相同的移动速度0.8 m/s。对移动速度v和泄漏时间t曲线积分，可得不同泄漏时刻爆炸上下限的位置坐标，为爆炸危险区域的划分提供了参考。

图8 不同管输压力时最低爆炸极限移动速度Fig.8 Moving velocity of minimum explosion limit under different pipeline transportation pressures

3.4 环境大气压对天然气扩散的影响

大气压随着四季气候更替和昼夜温差发生微小的变化。一般来说，随着气温和湿度的降低，大气压会增大，反之降低。刘虎生[24]指出最大的负压差14 kPa出现在夏季的下午。当大气压下降时，管廊两端和排风口的压力变化较管舱内变化显著，导致管舱产生内外压差，从而影响管舱内天然气的扩散。以p=200 kPa为例，改变管廊两端及排风口的边界条件，模拟标准大气压(101 325 Pa)和低于标准大气压14 kPa(87 325 Pa)下的天然气扩散规律。

监测报警器可知，2种工况下最先响应的装置均是在顺风侧方向x=7.5 m处的报警器，而且工况2比工况1的报警时间更短，说明若泄漏时刻发生在夏季下午，会比正常大气压下的报警响应更灵敏，缩短报警时间有利于及时发现泄漏。

如图9所示，当泄漏时间相同时，工况2天然气扩散距离均大于工况1，且在t=54 s时，幅值最大为10.1%；当t=126 s时，2种工况的扩散距离到达各自极值，因为在进风口风速吹扫作用下，天然气向逆风侧扩散时动能逐渐减小，大气压的降低导致逆风侧的扩散距离增加，从而延长总扩散距离。

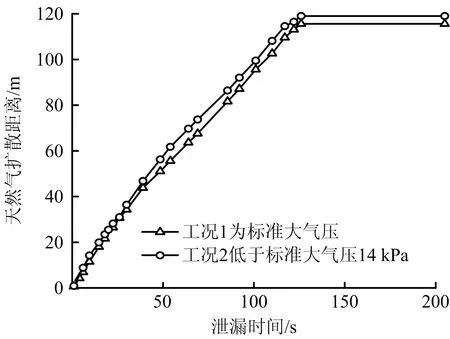
图9 不同环境大气压的天然气扩散距离Fig.9 Diffusion distances of natural gas under different ambient atmospheric pressures

3.5 解除报警时间

解除报警时间定义为管舱全部空间的天然气质量浓度值低于报警浓度值，即质量分数为0.6%。紧急切断浓度设定值不应大于其爆炸下限值的25%，换算成质量分数为0.9%。

为了分析风速对解除报警时间的影响，依次选择4，5，6，7,8 m/s作为目标风速，以泄漏总时长t=25，1 500 s 2种工况的天然气浓度分布作为初始值，其余条件与3.1节内容一致。

由图10可知，解除报警时间随着进风口风速的增大而减小。解除报警时间t与进风口风速v呈近似线性函数关系：泄漏总时长25 s：t=418-40.5v；选择4～8 m/s的风速均能够在300 s内解除报警；泄漏总时长1 500 s：t=1 242-125.5v。建议选择8 m/s作为进风口经济风速，使得用最小的通风量就能将解除报警时间控制在300 s以内。

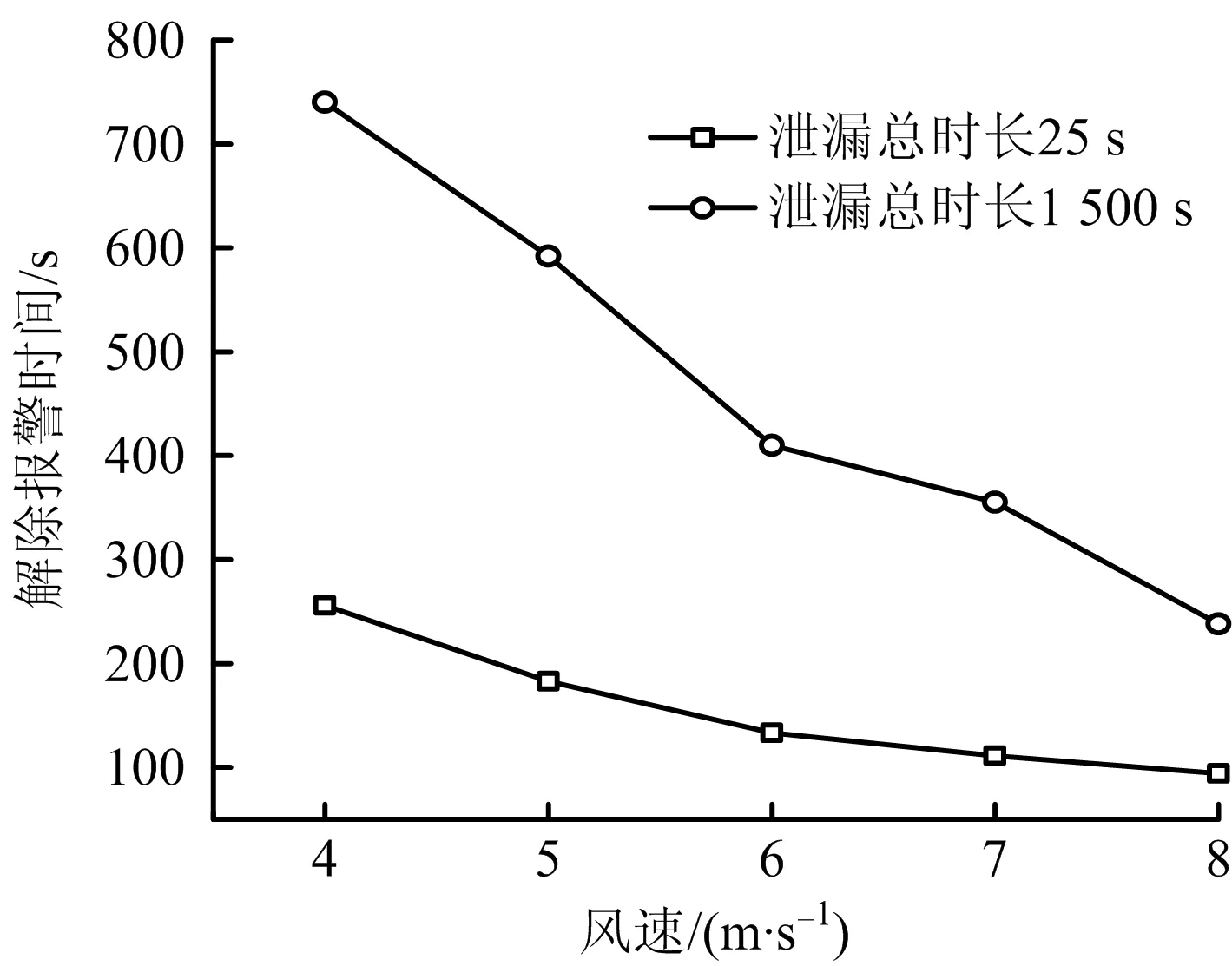
图10 不同泄漏时长的解除报警时间对比Fig.10 Comparison of release alarm time under different leakage time

4 结论

1)当泄漏孔径为20 mm，通风速度为1.92 m/s，且泄漏源处于2个报警器中间时，管输压力为200，400，800 kPa时报警时间分别为10.4，6.7，4.5 s。3种管输压力下最先响应的报警器均是x=7.5 m处，即顺风侧方向距离泄漏源最近的报警器。

2)不同管输压力的天然气朝逆风侧扩散时，扩散距离极大值随初始喷射速度的增大而增大。环境大气压的降低不仅会缩短报警装置的首次报警时间，还通过增加逆风侧扩散距离而延长总扩散距离。

3)天然气爆炸极限移动速度与管输压力成正比，通过预测爆炸危险区域的实时位置，有利于在事故抢险救援中准确地指导爆炸危险区域的划定，在该区域内杜绝任何火源以使爆炸可能性降到最低。

4)解除报警时间与进风口风速呈近似线性关系。可根据不同的泄漏初始状况和管廊周边环境选择最佳风速，为现场救援队伍对通风量及解除报警时间的判断提供参考。