再论圆形断面临界水深的近似直接计算式
李 蕊, 郭旭新, 徐 松
(1.杨凌职业技术学院, 陕西 杨凌 712100; 2.西北农林科技大学, 陕西 杨凌 712100)
0 引 言
在水力计算中,经常会遇到求解圆形断面渠道的临界水深,对于此水深的方程结构比较复杂,实质为计算含参变量的超越方程,且未知量包含在三角函数中,求解难度非常大。自1990年开始,许多专家对圆形断面临界水深进行了大量研究,获得了一些成果,主要成果集中在两个方面:①引入临界水深的无量纲参数,通过对临界水深方程的数学变换,得到无量纲水深的近似直接计算公式[1-4];②采用迭代法计算,通过选取合适的迭代初值和迭代方程计算临界水深[5-6]。鉴此,本文应用数学软件Matlab优化拟合法得到一种较简洁且高精度的近似直接计算式。
1 圆形断面临界水深基本方程
水力学中临界流的基本方程为:
(1)
如图1所示,圆形断面的水力要素分别为:
过水断面面积
(2)
水面宽度
Bc=dsin(θ/2)
(3)
临界水深
(4)
其中:Q为流量(m3/s);Ac为临界流对应的过水断面面积(m2);Bc为水面宽(m);g为重力加速度(通常取9.81 m/s2);a为流速分布不均匀系数(通常取1.0);θ为临界水深对应的圆心角(rad);d为洞径(m )。
将式(2)、(3)、(4)代入式(1)得:
(5)
由此可见:要求出圆形断面临界水深hc,必须先从(5)式中求出θ,然后代入(4)式中求出临界水深hc,而(5)式为关于θ的含参数的超越方程,理论上无解析解。
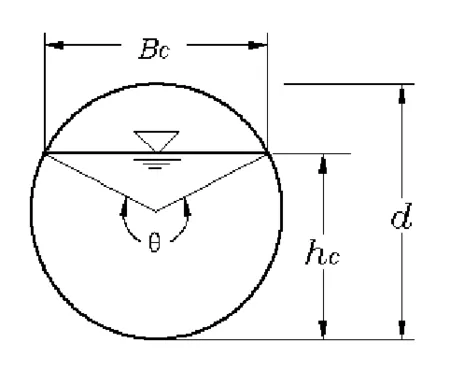
图1 圆形过水断面
2 圆形断面临界水深的近似直接计算公式
设
(6)
(7)
k可认为是无量刚参数,x可认为是圆形断面无量刚临界水深。
根据工程实际的要求及参考文献[3-5],x的取值范围为:0.05 >> k=[0 0.0001 0.0006 0.0018 0.0042 0.0085 0.0154 0.0258 0.0405 0.0606 0.0872 0.1216 0.1654 0.2209 0.3820 0.5044]; >> x=[0.05 0.10,0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.80 0.85]; >> plot(k,x,'go') >> k1=log(k); >> x1=log(x); >> plot(k1,x1,'r') >> cftool 由kx的散点图(图2所示)可见,kx之间的函数关系为: x=akb (8) 对原始数据进行取对数处理,得到数据k1与x1,借用拟合工具箱cftool得到k1、x1之间的函数关系为: x1=0.2557k1+0.02105 (9) 拟合图像如图3所示。 对式(8)两边同时取对数得到: lnx=lna+blnk (10) 比较(9)与(10)得到: lna=0.02105⟹a=e0.02105⟹a=1.0213 b=0.2557所以, x=1.0213k0.2557 (11) 将其代入(7)式,可得圆形断面临界水深的近似直接计算公式为: hc=x×d=1.0213k0.2557×d (12) 图2k-x散点图 图3k1-x1拟合图像 近几年求解圆形断面临界水深的近似直接公式很多,就简捷、通用、计算精度高这三方面考虑,有孙建公式和王正中公式相对较好,下面就和本文公式作一比较: ②孙建公式[4] ③本文公式hc=1.0213k0.2557×d 根据参考文献[3-5],x的取值范围为:0.05 表1 圆形断面无量纲临界水深误差计算表 根据表1,在0.05 从公式结构上来看,孙建公式最为复杂,本文公式最为简捷。 从公式的适用范围上来看,孙建公式、王正中公式和本文公式都能满足工程实际要求。 由此可知本文公式结构简捷,误差小,适应范围广。 以文献[1]为例,某圆形断面的引水式电站输水隧洞,洞径d=15.0 m,求设计流量Q=500 m3/s时的临界水深。 解:由(6)得: 由(12)得: hc=1.0213k0.2557×d=6.4283m 用孙建公式和王正中公式分别计算本例,结果见表2。 表2 临界水深计算 从例题的计算过程可见,本文公式计算步骤简单,仅需两步就可以求出临界水深;从上表的误差比较可见,本文公式相对误差仅为为0.012﹪;从公式的简捷程度可见,本文公式最为简捷。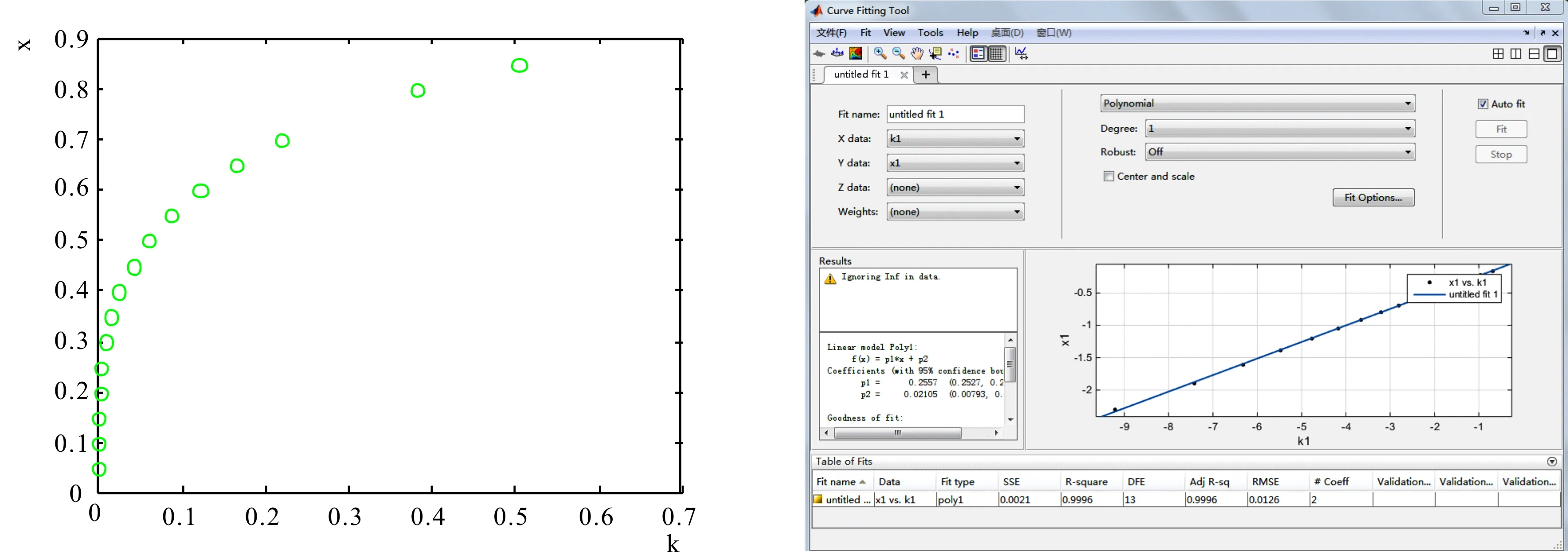
3 精度评价
3.1 近几年得到的近似公式

3.2 公式误差计算

4 工程实例


