频域积累耦合LMS的噪声消除方法

吴连军，郝惠敏

(1.太原理工大学机械与运载工程学院，山西太原 030024；2.教育部暨山西省新型传感器与智能控制重点实验室，山西太原 030024)

0 引言

在工程领域，机械设备故障对应的各类特征信号往往以某种方式与其他信号混合，使得特征信号相当微弱，同时，设备在工作时，又有强噪声干扰[1]。因此，采集到的信号多为信噪比(signal to noise ratio，SNR)很低的微弱信号，包含许多尖峰或突变部分，信号频谱与噪声频谱也往往重叠，分布在整个频域内，严重影响信号特性的提取。对低信噪比微弱信号处理时，传统的傅里叶变换无法表征其时频特性，对突变信号的灵敏度也很差[2]；小波变换应用广泛，但对低信噪比以及信号与噪声频带重叠的信号处理效果很差。另外，小波基、阈值函数、分解层数的选择也会影响处理结果，往往小波基、阈值函数确定了，信号的去噪特性就固定了，存在很大的局限性[3]。近年来，最小均方算法(least mean square，LMS)因其计算量小、收敛速度快、失调量小、不受不相关噪声干扰等特点而被广泛关注，它克服了传统去噪方式的局限性，能最大程度地保留信号细节特征[4]，可以对低信噪比噪声信号进行初步对消处理，但效果还不够理想。

针对以上问题，本文提出一种频域积累耦合LMS算法的低信噪比噪声消除方法，结合两种算法的优势，在利用频域积累提高信噪比的基础上，再通过LMS算法做进一步的去噪处理。经过仿真和实验验证，该方法可以有效提取低信噪比振动信号的特征信息。

1 频域积累

频域积累先将信号变换到频域中，然后在频域中进行信号累加。在不同时间段内选取相同时间长度的信号，分别进行固定点数的快速傅里叶变换 (FFT)，然后再将相应频率成分进行频域累加。离散傅里叶变换定义为[5]：

(1)

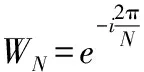
令N=M×L，M为积累次数，L为傅里叶变换点数，则频域积累的计算式转换为

(2)

式中xm(l)为第m次积累的信号。

2 LMS算法

由Widrow和Hoff提出来的LMS算法是自适应滤波算法中的一种，是在维纳滤波理论上运用速下降法后的优化延伸。

LMS算法的最终目标是通过调整系数，使输出误差序列e(n)=d(n)-y(n)的均方值最小化，其中y(n)表示算法输出量,d(n)表示理想信号，并根据此结果来修改权系数wk(n)。误差序列的均方值又叫“均方误差”(mean square error，MSE)。算法核心迭代公式如下[6]：

e(n)=d(n)-X(n)TW(n)W(n+1)=W(n)+2μe(n)X(n)X(n)=[x(n),x(n-1)…x(n-L)+1]TW(n)=[w(n)0w(n)1…w(n)L-1]T

(3)

式中：e(n)为误差;d(n)为期望输出值;L为滤波器阶数;μ为步长因子;W(n)为n时刻的自适应滤波器的权系数;X(n)为时刻n的输入信号矢量。

LMS算法的主要优点在于不必重复使用数据，也不必对相关矩阵和互相关矩阵进行运算，只需要在每次迭代时利用输入向量和期望响应即可，结构简单，易于实现，而且在解决许多实际的信号处理问题时，LMS 算法不受不相干噪声干扰。但仍有其自身的缺点，在处理低信噪比噪声时，稳定性较差，可能出现收敛缓慢甚至发散的问题。

最近几年，企业结构的调整一直是研究重点。企业改制也成为了重点研究对象。对于重组整合也进行了多种探索和尝试。在这些企业的改制中，涉及的领域较多，需要统一不同的部门，需要考虑到各方的利益。可能影响到权利的调整。这些领域的变动会带来国有资产管理、人事关系、社会福利保险等的问题。需要认真、审慎的对待这些问题。避免处于被动的局面。所以，对于这些企业的调整、重组，按照市场规律操作是必须的。

3 频域积累耦合LMS算法的去噪方法

对于低信噪比信号，频域积累可以有效提高其信噪比，得出关键特征频率，却往往需要较多的积累次数，而且随着积累次数的增加，信噪比的提升效率会降低。另外，积累后的信号总会含有较多的高频噪声，影响特征频率的提取。但鉴于LMS算法的缺点，频域积累耦合LMS算法可以互相弥补自身缺陷，发挥各自优势，从而提高低信噪比信号的处理效果。

频域积累耦合LMS的噪声消除方法的主要过程如下：先将采集到的信号变换到频域中累加，在不同时间段内对相同时间长度的信号分别进行固定点数的快速傅里叶变换，然后再将相应频率成分进行频域累加。经此过程提高信噪比后，再利用LMS算法作进一步处理，通过调整LMS算法自身参数，使输出信号与输入信号之间的误差最小，最大限度地保留低信噪比信号的细节特征，进而得到理想的处理效果，准确提取信号特征信息。

4 去噪效果评价

原始的纯净信号经加噪后再去噪，其降噪效果可用信噪比大小来衡量，也可采用平滑度指标来区分去噪效果。信噪比是指有用信号功率与噪声功率之比值，具体计算公式如下[7]：

(4)

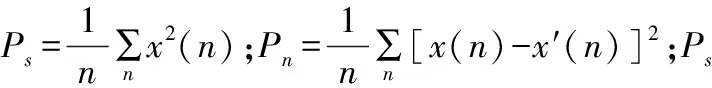
平滑度指标是指去噪后信号的差分数的方差根与原始信号的差分数的方差根之比，记为r。

(5)

式中：x(i)为原始信号；x′(i)为含噪信号分解重构后的信号。

平滑度指标的数值越小，信号越光滑，去噪效果就越好。

文中针对不同的信号处理方法，以信噪比SNR作为第1评价指标，平滑度r作为第 2 评价指标，在其他参数相同的情况下，衡量各个方法的去噪效果，选取最优的去噪方案。

5 仿真及结果分析

xn=sin(2πtf/fs)

(6)

在生成的原始信号基础上，利用awgn()函数产生不同信噪比的噪声信号，最后对得到的信号利用不同的方法进行处理。图1(b)为信噪比SNR=-15 dB的信号，从图中可以看出，原始信号在噪声信号中几乎完全淹没，无法提取特征信息。

(a)原始信号

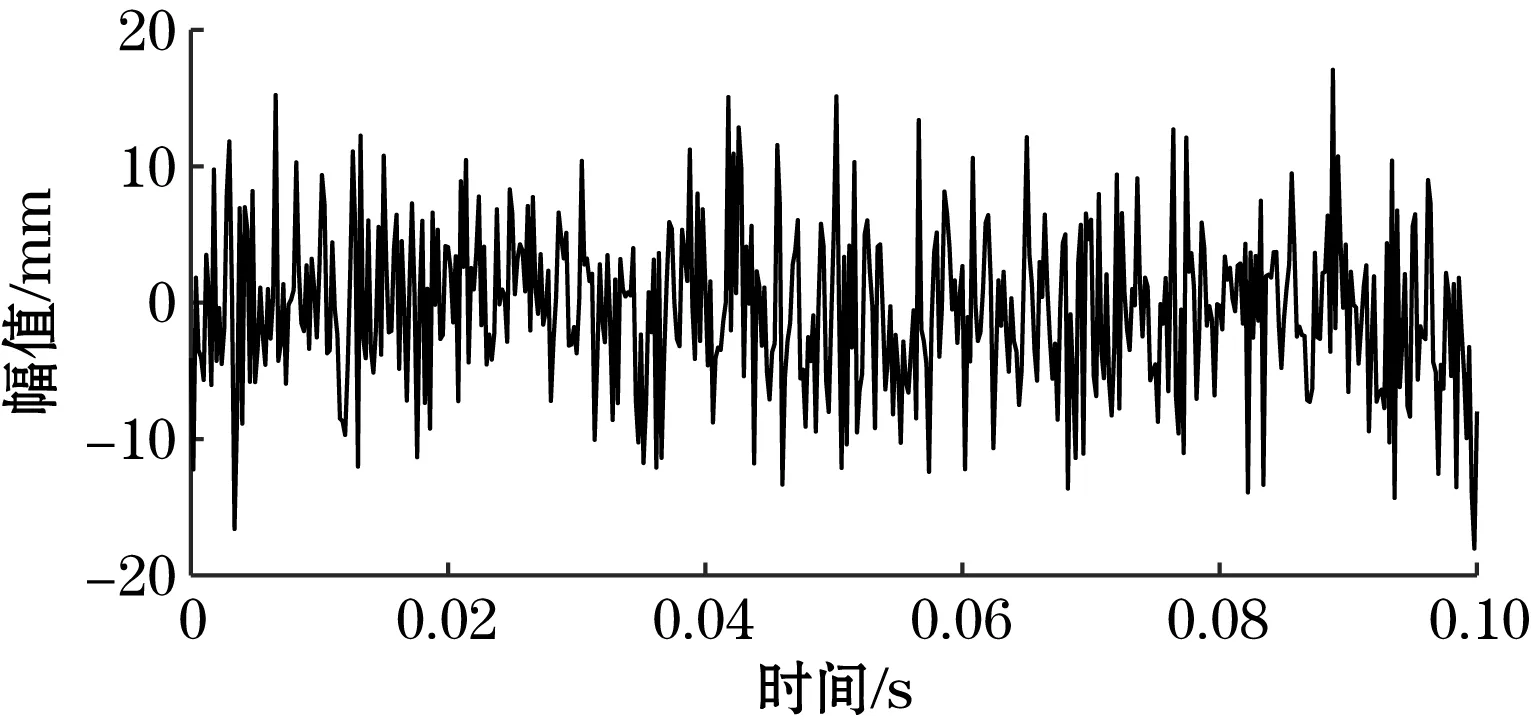
(b)噪声信号图1 仿真中原始信号及噪声信号

5.1 频域积累去噪

基于仿真，对含噪信号进行不同次数的频域积累后得到的结果，如图2所示。可以发现，频域积累5次后信噪比得到提高，经计算，SNR提升到了3.75 dB。经过20次、50次频域积累后，信噪比分别达到SNR=7.68 dB，SNR=10.37 dB。可见，随着积累次数的增多，对噪声的抑制效果逐渐变好，信噪比得到提高。但如表1所示，当次数达到一定值之后，继续积累对信噪比的提升程度越来越小，平滑度改善较小，而且高频噪声始终存在，所以单纯地依靠增加积累次数提高信噪比并不是好的选择。

表1 不同积累次数下的处理效果

5.2 LMS算法

为了探究LMS算法对低信噪比噪声的去噪能力，通过awgn()函数，分别生成信噪比为-15 dB，-10 dB，0 dB的噪声信号，利用LMS算法分别处理后，信号的信噪比分别达到SNR=-1.067、SNR=1.836、SNR=6.623，都有了一定程度的提高，但并不足以达到提取信号特征信息的目的，造成这种问题的原因在于LMS的固有特性，在噪声干扰较强时容易发散、稳定性差。

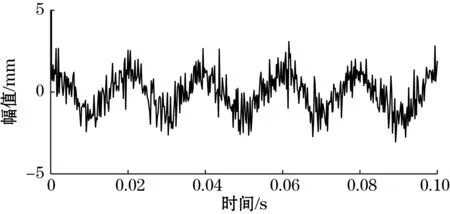
(a)频域积累5次

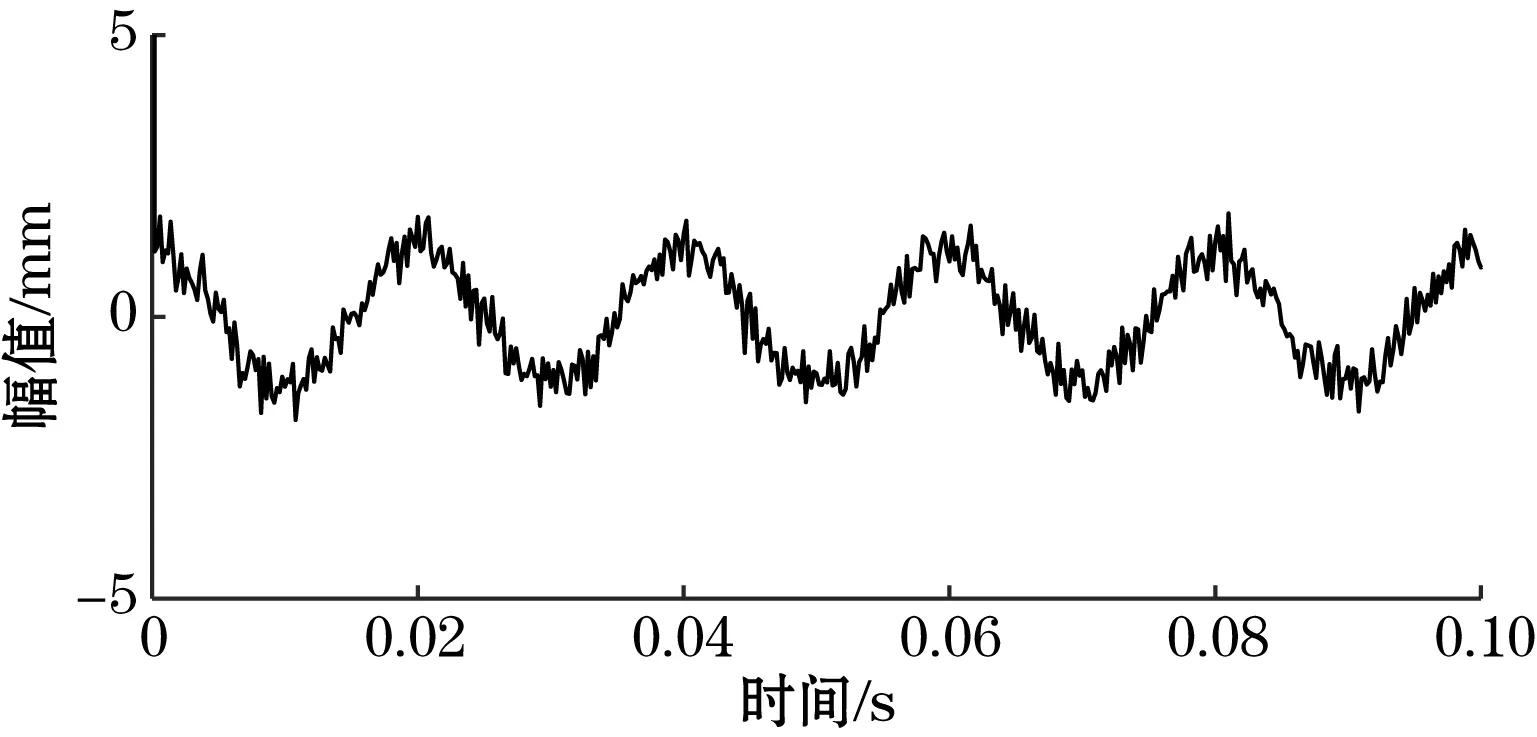
(b)频域积累20次

(c)频域积累50次图2 不同频域积累后的仿真结果

图3为利用LMS算法对信噪比SNR=-15 dB的噪声信号进行处理的结果。设置参数迭代步长μ=0.0015，迭代次数50。经过LMS算法处理后可以得到图3所示的信号效果比较图，可以看出，LMS算法对低信噪比信号的处理结果并不理想，处理前后误差很大，难以得到准确信息。

图3 LMS算法信号处理效果对比

5.3 频域积累耦合LMS算法去噪

频域积累耦合LMS算法的噪声处理方法，在于结合两种算法的优点，针对信噪比为-15 dB的噪声信号，首先通过频域积累的方式提高信号的信噪比，然后通过LMS算法作进一步处理，利用LMS算法的优势，更好地提取特征信息。图4(a)为频域积累与LMS结合去噪后的信号图，图4(b)为频域积累与LMS结合去噪后的效果分析图，可以看出，利用该方法处理过的信号误差显著减小，相比LMS算法，得到的信息更加真实可靠，可以较好地去除噪声，提取特征。

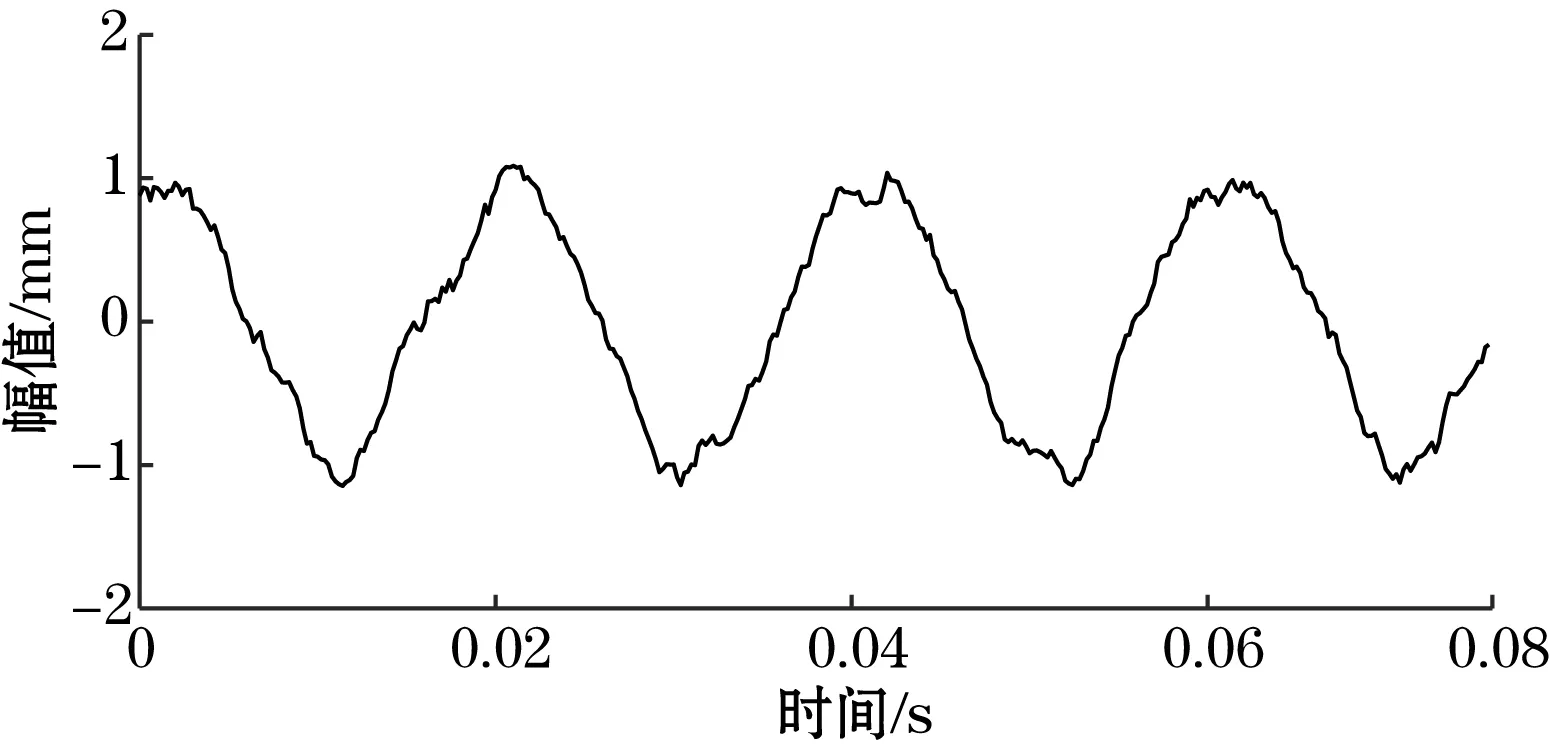
(a)频域积累与LMS结合去噪后信号

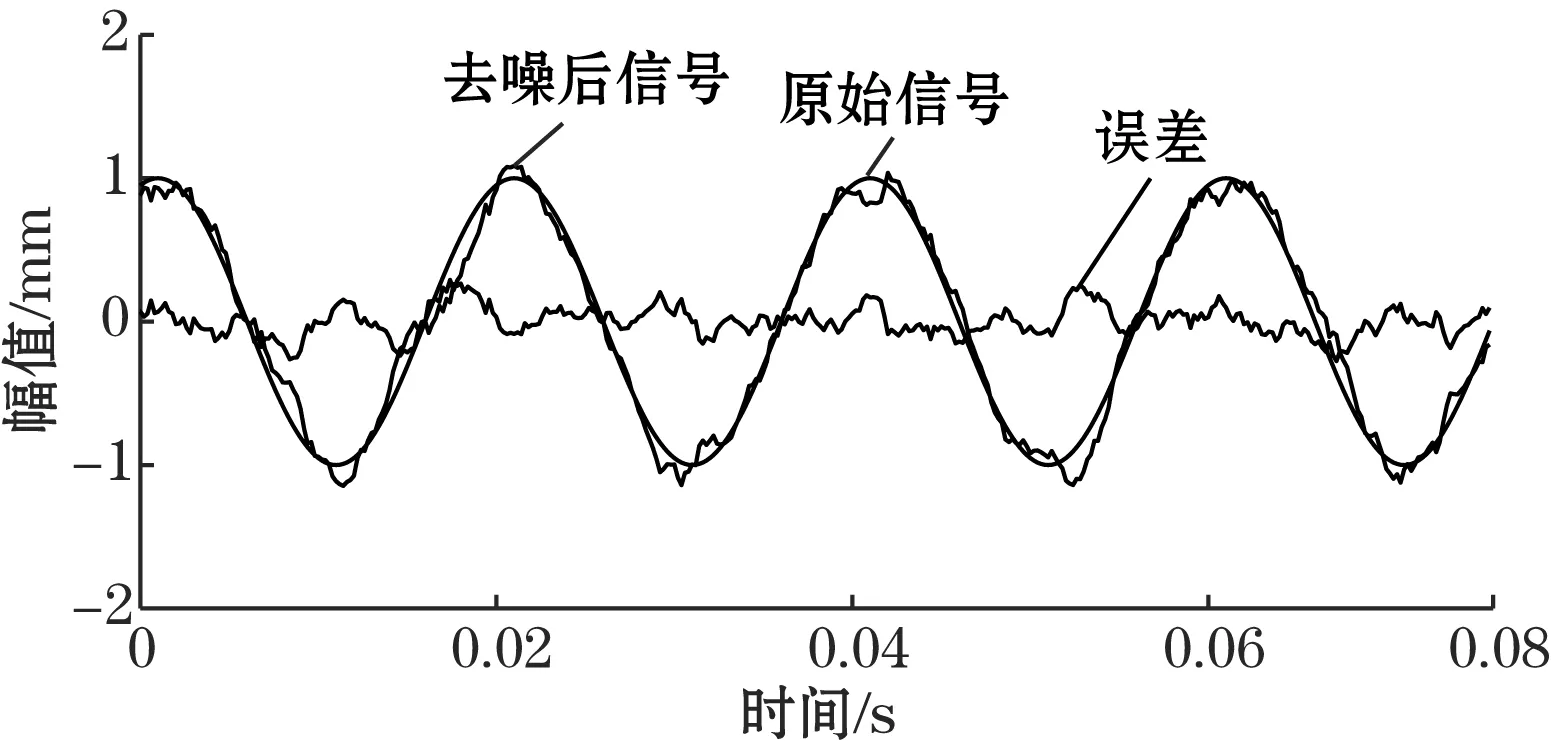
(b)去噪效果图图4 频域积累与LMS结合去噪后信号及去噪效果分析图

为了进一步验证频域积累耦合LMS的噪声处理方法对低信噪比信号处理的高效性，将其与小波变换处理效果做对比。小波变换处理低信噪比信号的结果如图5所示，从图中可以发现信号严重失真，许多细节特征也被平滑掉，在处理效果上与频域积累耦合LMS算法相比要差很多。

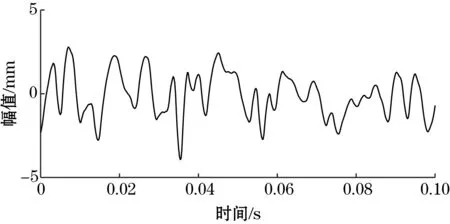
图5 Sym5小波去噪效果

最后对各信号处理方法的性能从信噪比、平滑度方面进行比较，如表2所示。

表2 各方法对噪声信号的处理效果

从表2可以看出，利用以上4种方法处理后的噪声信号信噪比都有了不同程度的提升，频域积累与LMS耦合方法的处理效果最明显，在保留信号细节特征的基础上，将信噪比提高到18.62 dB，平滑度低至0.007 3。

6 实验信号的去噪处理

为了验证该处理方法对实际应用中低信噪比噪声信号的处理效果，从带有故障的转子实验台上采集振动信号，并对其进行处理和验证分析。实验台如图6所示。

图6 转子实验台

实验台的主要组成有：三轴加速度传感器(测量垂直与水平方向的振动)、电动机(驱动转子旋转)、变频器、滚动轴承。设置转子实验台的电动机转动频率为50 Hz，采样频率5 000 Hz。采集到的原始信号如图7所示。

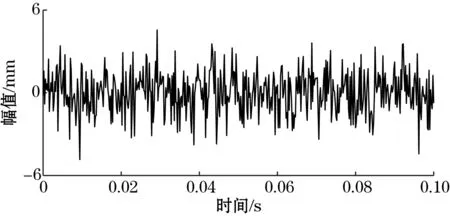
图7 实验采集信号

从图中可以看出，从故障实验台上采集到的信号与噪声互相混叠，噪声将信号淹没，难以提取特征信息。利用频域积累、耦合方法和sym小波对信号处理的结果分别如图8～图10所示。

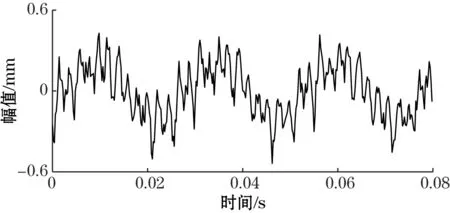
图8 频域积累后的信号

图9 频域积累耦合LMS去噪后的信号

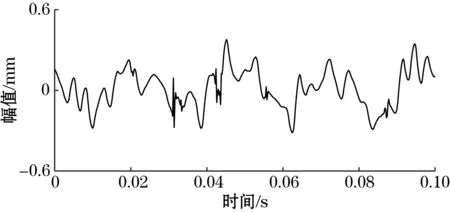
图10 Sym5小波处理后的信号

从图8和图9可以看出，噪声信号经过频域积累后，信噪比得到明显提高，但仍旧存在许多毛刺等杂波信号。而经过LMS算法做继续处理之后，振动信号可以清晰地识别出来。图10表明，利用sym5小波变换处理过的振动信号失真严重，许多细节特征被平滑掉。由此可见，频域积累耦合LMS算法对实验振动信号的处理效果很好。图11为实验信号的频谱图，可以看出，在实测环境中，各种干扰较多，难以从频谱中获取特征频率。经过频域积累耦合LMS算法处理后(图12)，效果明显改善，得出振动信号的特征频率为50 Hz。

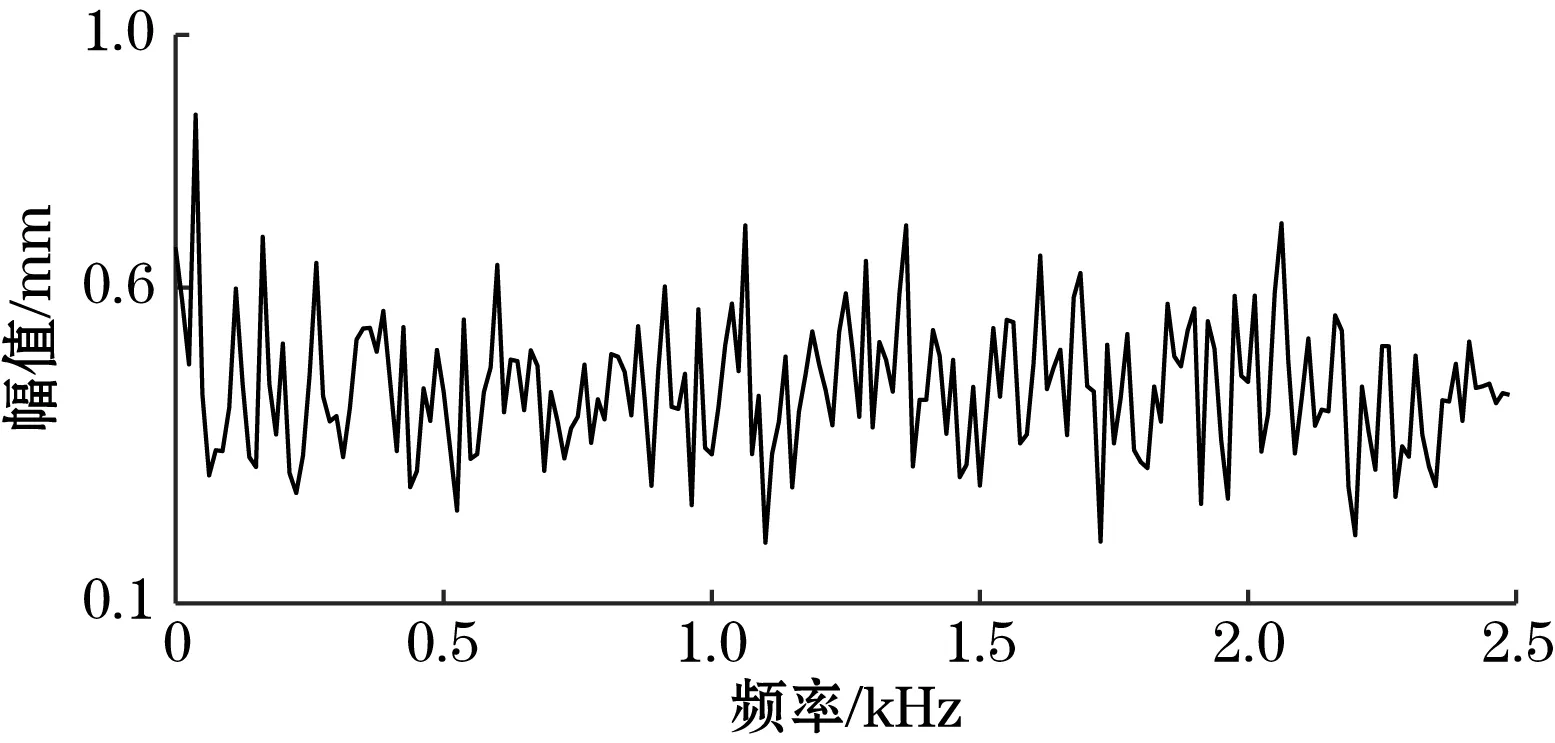
图11 实验信号频谱

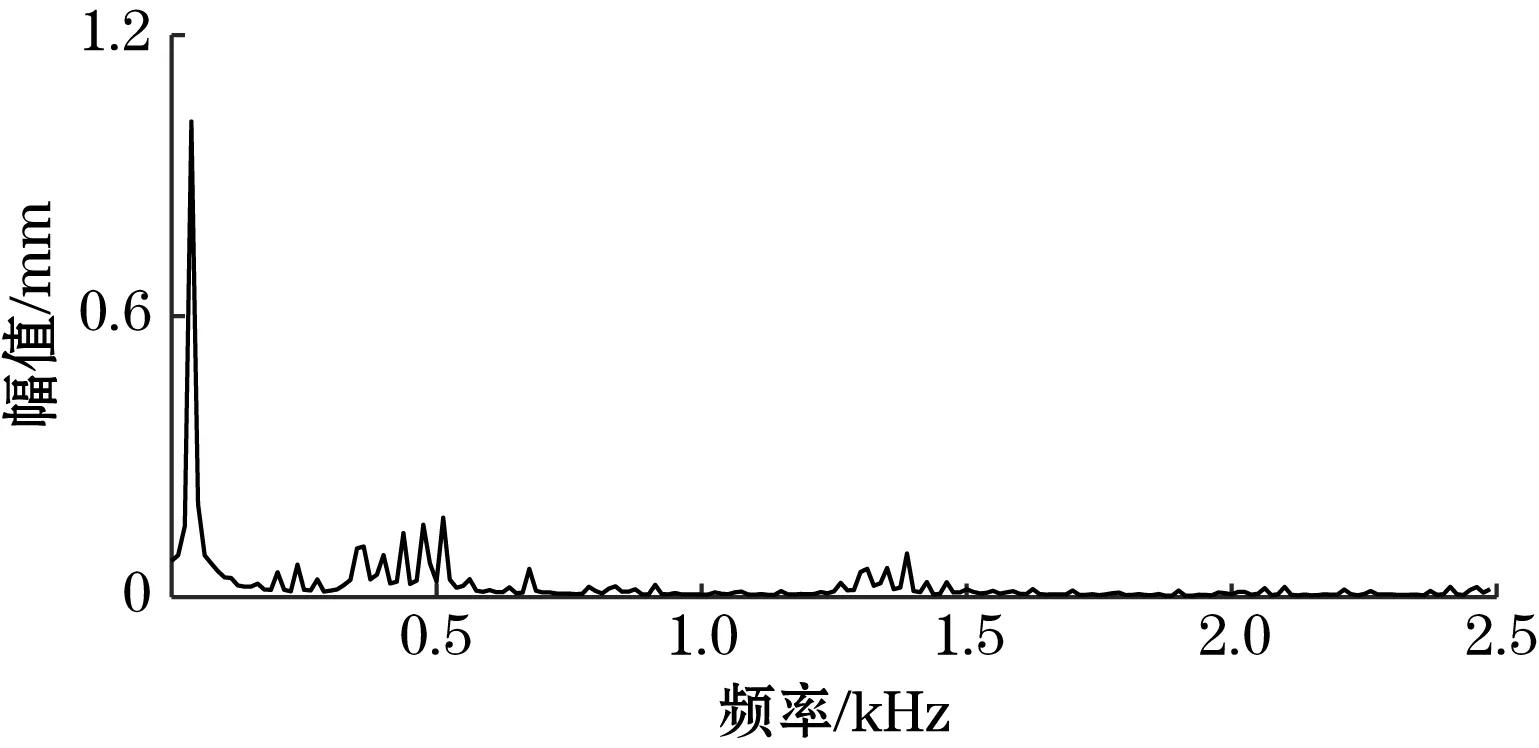
图12 频域积累耦合LMS算法去噪后信号

7 结束语

频域积累能有效提高信噪比，但需要比较多的积累次数。LMS算法不受不相干噪声干扰，能够很好地保留细节特征，但对低信噪比噪声信号处理效果较差。利用频域积累耦合LMS算法对低信噪比信号进行处理，不仅有效提高了信噪比，而且保留了信号的细节特征。仿真和实验表明，该方法可以有效提取低信噪比信号的特征信息，是一种很好的噪声消除方式。