基于PR控制的PMSM钢模板提升平台系统的研究

摘 要：在高层建筑钢模板提升控制平台中，为了满足钢模板在提升过程中稳定性和快速性的要求，对此本文提出了一种基于比例谐振控制静态坐标下的PMSM的控制策略，在利用传统的永磁同步电动机控制的基础上对实验结果进行验证。

关键词：PMSM;PR控制;钢模板

永磁同步电动机PMSM是一种非线性的数学模型，在用于提升装置的动力源时，其调速系统需要较好的控制精度和控制效果，而传统的PI控制难以满足其钢模板提升控制的要求。因此要达到钢模板平台的提升效果，需要对传统的PI算法进行改进。传统的同步控制器都是采用同步旋转坐标下进行前馈解耦PI控制，但是在系统的运行中，系统的电阻、电感的电机参数会随着磁路温度等众多因素升高而改变，使系统的精确度下降，满足不了钢模板提升平台高精度的要求。為此，本文提出了一种基于比例谐振控制的静止坐标系下的矢量控制策略。

1 传统的PI控制策略

当前传统的矢量控制方法主要包含三个部分，转速环PI调节器、电流环PI调节器和SVPWM算法。

在转速环PI调节部分，为了便于转速环的参数整定，三相PMSM的电机运动方程为：

Jdωmdt=32pniqiqLd-Lq+ψf-TL-Bωm

若采用传统的PI调节器，则转速环控制器的表达式为：

i*q=KPω+Kiωsω*m-ωm-Baωm

在电流环调节部分，定子电流id、iq分别在q轴和d轴方向产生交叉耦合电动势，id、iq完全解耦公式为：

ud0=ud+ωeLqid=Rid+Ldddtid

uq0=uq-ωe（Ldid+φf）=Riq+Lqddtiq

对该式进行拉普拉斯变换可得：

id（s）

iq（s）=R+sLd 0

0 R+sLq-1ud0（s）

uq0（s）

2 基于比例谐振PR控制的矢量控制策略

对于系统的电阻、电感的电机参数会随着磁路温度等众多因素升高而改变，使系统的精确度下降等问题，提出了一种基于比例谐振控制的静止坐标系下的矢量控制策略。对于直流控制系统，在同步坐标系下的PR控制器的坐标函数为：

GPI（s）=12GPI（s+jω0）+GPI（s-jω0）=Kp+2Kiss20

其中若ω0为信号的角频率时，GPI（s）的幅值可以表示为：

GPI（s）s=jω0=K2p+2Kiω0-ω20+ω20

由于上述公式的幅值的大小可以随意变化，进而可以根据具有同频信号进行零稳态误差控制，但这种情况仅存在于理想状况，由于PR控制器本身存在的问题和自身的局限性，提出了一种改进的准PR控制器，其传递函数为：

GPR（s）=Kp+2Kiωcss2+2ωcs+ω20

同步坐标下PR传递函数为s函数，在对三相PMSM系统进行控制时，为了使离散化过程更为简便，控制效果更为明显，本文的离散化过程仅针对谐振控制器，利用双线性变换，公式变换为：

s=2Ts1-z-11+z-1

将其带入PR传递函数，可得：

GR（z）=b0+b1z-1+b2z-21+a1z-1+a2z-2

整理后得到差分方程：

y（k）=b0e（k）+b2e（k-2）-a1y（k-1）-a2y（k-2）

该方程实现了对误差信号的稳态控制，其控制比较简单且实现容易，对于钢模板提升过程中稳定性和精确性都有很好的控制，满足工程项目的要求。

3 系统仿真模型的仿真结果

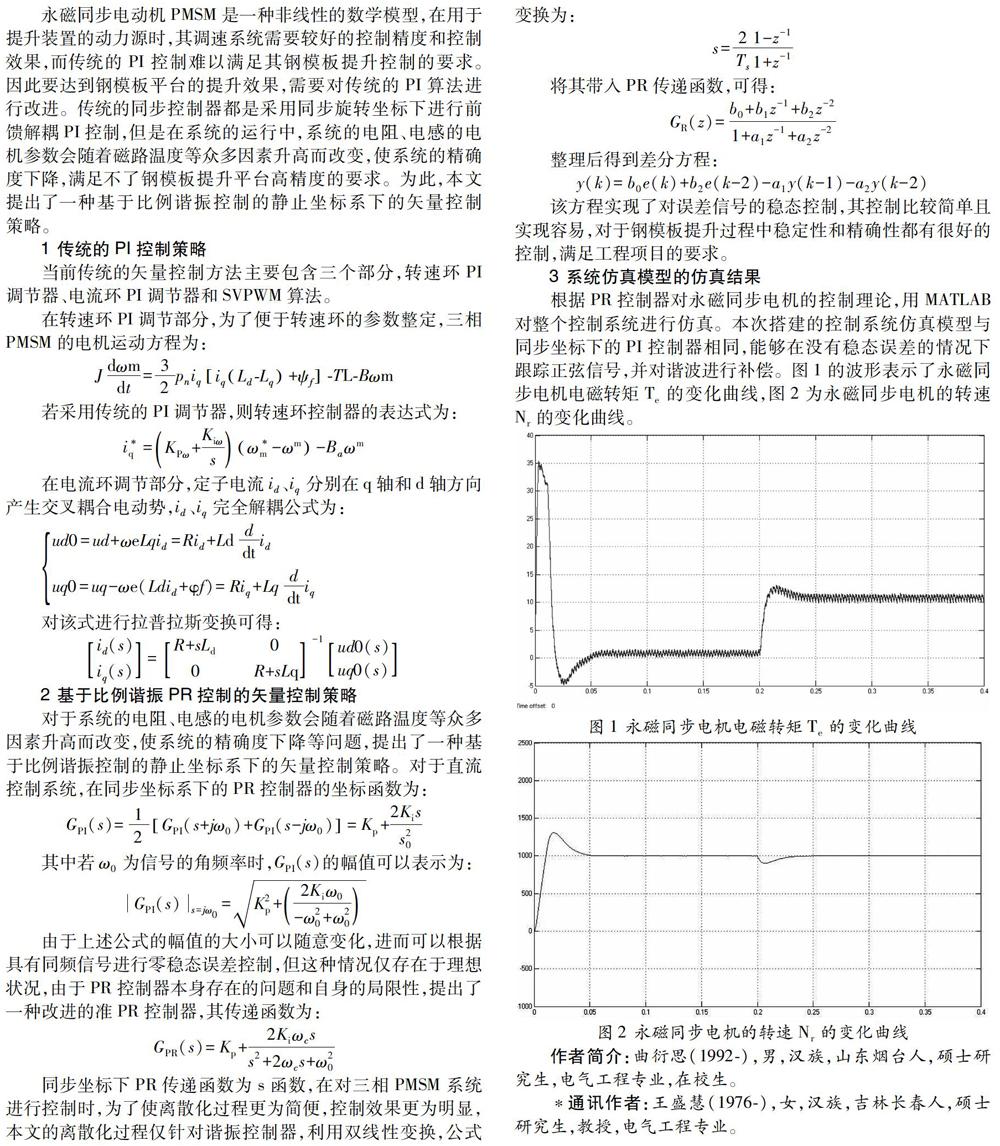
根据PR控制器对永磁同步电机的控制理论，用MATLAB对整个控制系统进行仿真。本次搭建的控制系统仿真模型与同步坐标下的PI控制器相同，能够在没有稳态误差的情况下跟踪正弦信号，并对谐波进行补偿。图1的波形表示了永磁同步电机电磁转矩Te的变化曲线，图2为永磁同步电机的转速Nr的变化曲线。

作者简介：曲衍思（1992-），男，汉族，山东烟台人，硕士研究生，电气工程专业，在校生。

通讯作者：王盛慧（1976-），女，汉族，吉林长春人，硕士研究生，教授，电气工程专业。