双馈电机交交实时变频系统研究

摘  要： 双馈电动机因其在调速及节能控制中的诸多优点，使其在工业发展中具备广泛的应用前景。在雙馈调速系统中，一般常用交交变频器作为变频电源，因而对变频器输出电能的质量及频率切换响应速度有着较高要求。本文在双变量交交变频控制原理的基础上，对余弦交截法在线计算触发策略进行了优化改进，以触发交点纵坐标的幅值为参考，简化了触发时序在线计算过程，并在此基础上提出了频率间实时切换的变频方式，该方式具有较快的频率切换响应速度，可使频率间的实时切换过程变得平滑。基于此，在SIMULINK仿真环境下搭建双馈电机调速系统的仿真模型，对本文提出的改进后的在线触发策略及频率间实时切换方式进行验证，仿真结果表明，改进后的在线触发策略及频率间实时切换方式能够满足双馈电动机对调速性能的要求。

关键词： 交交变频器;实时切换;在线计算;双馈调速

中图分类号： TM343;TP391.9    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.10.029

本文著录格式：李亚民. 双馈电机交交实时变频系统研究[J]. 软件，2019，40（10）：129134

Research on Real-time Frequency Control System of Doubly-fed Machine

LI Ya-min

（Zhengzhou Institute of Science and Technology， Zhengzhou 450064， China）

【Abstract】： Doubly-fed motor has a wide range of applications in the industrial development. because of its advantages in aspecs of speed-regulation and energy-saving. The double-fed speed control system which commonly uses AC-AC frequency transformer as a variable frequency power， has a higher demand to the frequency power quality and frequency switching response speed. In this paper， based on the principle of bivariate AC-AC frequency conversion control， the online triggering strategy of cosine crossover method is optimized and improved. With the amplitude of the ordinate of the intersection as a reference， the on-line calculation process of the triggering timing is simplified. On this basis， the frequency Real-time switching strategy is proposed， which has a fast frequency switching response speed and can make The real-time switching process becomes smooth. Based on this， the simulation model of the doubly-fed motor speed control system is established in the SIMULINK simulation environment， in which the improved online triggering strategy and the real-time switching strategy are verified. The simulation results show that the improved online triggering strategy and frequency Real-time switching strategy is correct and feasible， which can meet the requirements of the doubly-fed motor on the speed performance.

【Key words】： AC-AC frequency converter; Real-time switching; Online calculation; Double fed speed regulation

0  引言

双馈调速系统是将绕线式感应电动机的定子接工频电源，转子绕组接一个幅值、频率、相位均可调节的变频电源，从而构成定、转子双向同时馈电的调速系统。双馈调速一般常用交交变频器作为变频电源，对变频器输出电能的质量有着较高要求。为使输出的波形具有较好的余弦度，交交变频器常用余弦交截法求取开关器件的触发时刻。但是余弦交截法计算较为复杂，难以实现实时在线计算[2]。在计算机处理技术快速发展的今天，为了取得比较好的控制效果，对晶闸管等功率器件触发的实时性、精确度以及频率切换响应的快速性都有着较高的要求。为便于在计算机中实现实时在线计算，文献[3]中提出一种近似余弦交截法的在线求解触发交点算法，该方法用三角波代替参考电压波和同步余弦波，把复杂的反三角函数方程的求解过程简化为求解直线方程，易于实现触发时刻的在线计算[3]，其计算过程以触发时间为参考，对于频率间的切换采用采用固定点切换方式，频率切换的实时性较差。为此，本文在文献[3]算法的基础上，提出了一种以触发交点的纵坐标为参考的在线计算改进算法，并以此为基础，提出了基于实时切换方式的交交连续变频方法。改进后的在线计算策略及实时变频方式不仅能够简化在线计算的过程，而且能够提高频率切换响应的实时性，实现实时连续变频，满足双馈电动机对于调速性能的要求。

1  双馈电机调速原理

在稳态运行时，电机定转子旋转磁场在空间上是相對静止的，定子磁场以旋转，转子磁场相对于转子的旋转速度，上式说明，因为一般小于0.5，所以在低频段采用交-交变频器最合适。

图1为双馈电机的等效电路根据电机等效电路列出平衡方程：

（1）

电机的转子侧串入后，转子的计算公式为：

（2）

电机的转子侧有功和无功电流公式分别为：

（3）

（4）

由上述公式可见通过控制就可以改变电机的和控制电动机的转速和功率因数。

由此可见，双馈异步机比较以往的定子侧全压、全功率的变频方式，具有速度可调，功率因数可调，且需要变频器功率小、电压低、特别适合低频段调速等优点。

2  双变量交交变频控制原理

双变量控制理论是指在角控制基础上加上对脉冲宽度的控制，即对触发脉冲的后沿进行控制，从而实现了双变量相控变流器及变频器的自然无环流控制[4]。

双变量控制理论利用余弦交截法，当晶闸管正组触发，电流为正时，取基准电压波和同步余弦波的下降沿交点为触发脉冲点，可以实现正组晶闸管自然无环流换相。当电流过零点处时，控制电流在一组反并联的晶闸管上实现自然换流。当电流为负时，控制晶闸管反组触发，取基准电压波和同步余弦波的上升沿交点为触发脉冲点，可以实现负组晶闸管自然无环流换相[5]。

3  触发时刻在线计算改进算法

由于双变量六脉波交-交变频器三相触发规律完全相同，在这里仅以U相的切换为例进行分析。

图2为改善后的U相晶闸管触发时刻示意图，图中TA、TB、TC、TD、TE、TF分别为A、B、C、D、E、F六相电源的同步波，则相邻两同步波在横轴上交点的间隔为1/300，幅值为1，UC为U相参考电压波，幅值为（0<≤1），点A和点A1为参考电压波的波谷，点C为参考电压波的波峰，点B和点D分别对应着U相参考电压波上的电流过零时刻。参考电压波幅值和换流点对应的纵坐标幅值将一个周期分成四段，分别为AB，BC，CD，DA1，通过触发交点对应的纵坐标幅值与电压幅值r和换流点对应的纵坐标幅值间的比较来确定换流点、波峰和波谷的位置。

从图中容易求得同步波的斜率=，参考波的斜率=（上升沿斜率符号取“+”，下降沿斜率符号取“–”），各段内相邻两点间的幅值增量及时间增量文献[3]中已有详细计算说明，本文不再详细复述，由文献[3]中计算可得=，=。当同步波与参考波交点处于AB段和CD段内时，及分母符号取“–”，当同步波与参考波交点处于BC段及DA1段内时，及分母符号取“+”。如图2所示，设AB段内当前触发交点为，则根据当前触发交点的横坐标、及纵坐标及所在段内相邻两点间的幅值增量及时间增量即可求出该段内下一个触发交点的坐标和，即下一个触发交点的坐标为+，=+。

对于换流点处的计算，以B点处为例，如图2中所示，设当前触发交点的横坐标为，幅值为，为相电流由负过零变正时所对应的换流角值，则换流点B处幅值，则在点触发A相反组晶闸管A-，当<且>时，可以判断换流点B处于和之间，此时根据双变量控制原理，需要在点后延时0.5ms，然后触发A相正组的晶闸管A+，使电流可以在两只反并联的晶闸管上实现自然换向。电流换向后，首先要在处触发B相的正组晶闸管B+，根据线性关系，可得出到处的时间增量和幅值增量，其中= =，从而可求得电流换向后第一个触发点点的横坐标 +及其纵坐标的幅值=+。由于此时的值已大于换流点处幅值，且电流为正，故应按照BC段相应的算法依次计算BC段内各触发交点的触发时刻及其幅值，如图2所示，在参考波上升沿BC段内，当前触发交点的横坐标为，幅值为，和分别为BC段内任意两点间对应的时间增量和幅值增量，则下一个触发点的横坐标可表示为，而其相应的纵坐标可表示为=+。

对于波峰C、波谷A1处的计算，以参考波峰值C点为例，如图2所示，C点幅值为，当判断BC段内当前触发交点的坐标幅值<且 >时，可以判断波峰C处于和之间。根据线性关系可以得出过峰值后下一个触发点相对于点处的时间增量及幅值增量，如式（5）和式（6）所示：

（5）

（6）

所以峰值过后点的触发时刻，也即其横坐标为+，其对应的纵坐标幅值为=+。由于此时已过峰值，故接下来应按照CD段相应的算法依次计算CD段内各触发点的触发时刻及其幅值。

对于参考波下降沿CD段、换流点D处、DA1段及波谷A1处触发时刻及幅值的计算方法分别于与参考波上升沿AB段、换流点B处、BC段及波峰C处触发时刻及幅值的计算方法类似，由于篇幅有限本文不再详细说明。由以上分析可知，改善后的在线计算方法，以触发交点纵坐标幅值为参考，按点进行计算，大大简化了触发时序的在线计算过程，使程序调试方便、简单。

4  频率间实时切换方式

由以上分析可知，本文提出的在线计算改进算法实现了交-交变频触发时刻按点在线计算的功能，为频率间实时切换方式的实现提供了有利条件。交-交变频输出频率间的切换，实际上对应着不同频率参考电压波间的切换。实时切换方式即在接收到频率变化命令后，立刻进行参考电压波的变换。为保证变换过程的平滑过渡以及变化后变频器的三相输出对称，实时切换方式在实现频率变化时，按照相位相等的条件，从当前频率对应的参考电压波切换到指定频率对应的参考电压波。根据图3，频率切换时刻出现在参考电压波上的位置可分成四种情况，分别对应着：切换时刻出现在AB区间;切换时刻出现在BC区间;切换时刻出现在CD区间;切换时刻出现在DA1区间。由于交-交变频器输出三相的频率切换规律完全相同，在这里仅以U相的切换为例进行分析。如图3所示为频率切换命令  出现的时刻在参考电压波AB区间时频率间切换示意图。

如图3所示，对应着频率为的相参考电压波，幅值为（0<≤1），点、为和同步波上升沿的交點，频率切换指令出现的时刻在图中的点与点之间。为切换后，频率对应的相参考电压波，幅值为（0<≤1），，，点、为和同步波BT、CT上升沿的交点，竖直线L1与和分别交于点与，点在当前周期的相位与在当前周期的相位相等，频率切换的响应从点后的下一个触发时刻开始。设当前触发交点的坐标为（，），由于在当前周期的相位与在当前周期的相位相等，所以可以方便的求得的坐标

为（，），由点可求得所在的同步波上升沿的直线解析式（7）;由点可求得所在参考电压波U2上升沿的直线解析式（8），如下所示：

（7）

（8）

联立式（7）、式（8），求得的坐标表达式如下：

（9）

（10）

点与点的时间间隔 和纵坐标间隔，则由点坐标很容易求得点坐标如式（11）、式（12）所示：

（11）

（12）

此时点在当前周期的相位与在当前周期的相位相等，频率切换的响应从点后的下一个触发时刻开始。同理，当频率切换指令出现在BC段、CD段以及DA1段内时，其对应的计算过程与频率切换指令出现在参考波上升沿AB段内时的计算过程类似，由于篇幅有限，在此亦不再详细列出。

5  仿真分析

5.1  双馈调速系统模型搭建

根据本文提出的在线计算改进算法及频率实时切换方式，结合双变量交交变频原理和双馈电动机的工作原理，在MATLAB/SIMULINK环境下搭建六脉波双变量交交变频双馈电机调速系统仿真模型，并对双馈电机启动过程和实时连续变频调速过程进行仿真。仿真中所用电机参数为：=2.2 Kw，=380 V，=50 Hz，=5.49 Ω，=6.78 Ω，= 6.7 Ω，=0.00069H，=0.0009H，=0.1152H。根据以上电机参数及双馈电机的调速原理，在SIMULINK中搭建双馈调速系统的仿真模型如图4所示。模型中主要包括电源模块、电机模块、晶闸管模块、S函数模块、检测模块、断路器模块等部分组成，六脉波交交变频器电源模块POWER有6相互错60度的交流电源组成，变频电路模块U、V及W由3相36个反并联晶闸管组成，每一项对应12个，在S-FUNC模块中利用MATLAB中的S函数对上述在线化算法进行编程，以根据双馈调速系统对交交变频器输出电压、频率以及频率间的实时切换命令的要求实现对各个晶闸管触发时刻的在线计算，而断路器模块主要通过控制其通断时刻，以实现转子侧变频电源的切入[6]。

5.2  双馈电机启动过程仿真

根据双馈电机的工作原理，采用双变量六脉波交交变频器来设计双馈电机的启动方案。因为双馈电机需要定转子双边馈电，其起动过程与同步电机相似，需要经过两个阶段即单边起动和牵入双馈。当电机单边起动后转速达到一定值时，加入交流励磁电流，牵入同步。双馈电机常用的启动方案有转子侧变频起动和定子侧降压启动。本文采用定子侧降压启动方案，定子侧降压启动方案是在转子绕组

先接入频敏变阻器，定子工频软启动，电机在某一合适的转速下稳定运行后，发出切换控制指令牵入双馈[7]。

图5为双馈电机在六分频下启动的转速波形，电机带2 N?m负载。定子电压为85 V，馈入前电机转速1320 r/min，在1s时切入双馈，同时通过断路器将定子侧电压幅值提升至工频311 V，电机经0.1 s短暂震荡后稳定运行于1250 r/min，启动过程结束。从图中可以看出，双馈电机成功切入双馈后双馈电机运行状态良好。

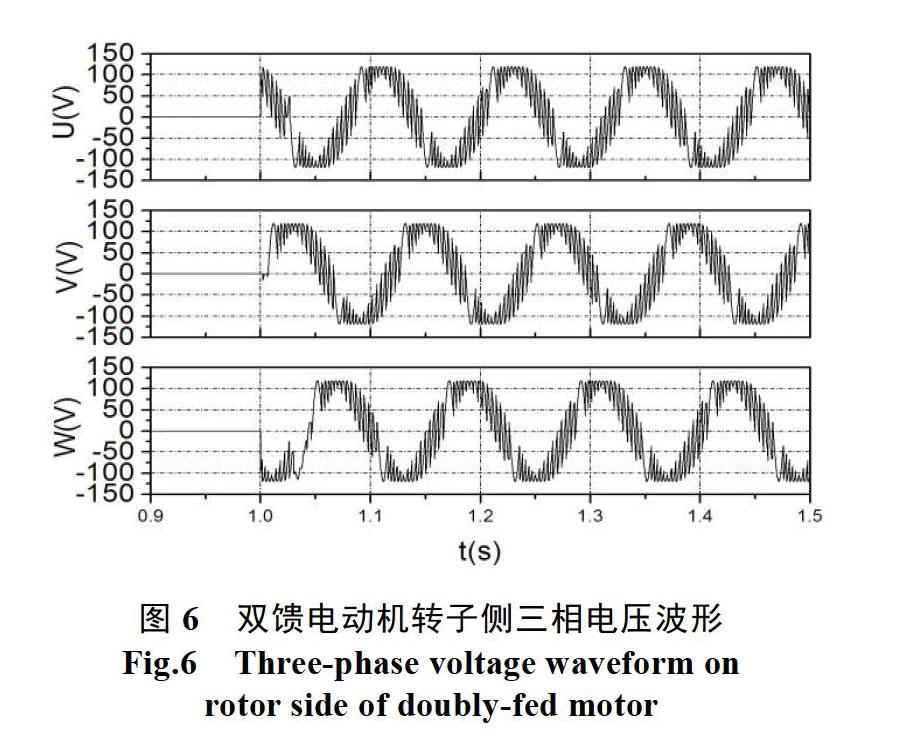
图6为馈入双馈后转子侧电压波形，由图中波形可以看出采用实时在线计算改进算法，可使变频器输出波形具有较为理想的对称度、余弦度及平衡度，能够很好的满足双馈电机对于变频电源波形质量的要求。

5.3  双馈电机连续变频调速过程仿真

根据双馈变频调速原理，他控制式异步双馈电机在稳态运行以后，定子侧电压幅值、转子侧电压幅值和负载大小对电机的转速均无影响，转速只与转子侧变频电源的频率有关，并与变频电源的频率呈线性关系[8]。所以在异步电机起动并成功切入双馈稳定运行以后，通过改变变频电源的频率大小就可以调节电机的转速。

连续变频调速仿真中，采用本文提出的实时频率切换方式，来进行连续变频调速。首先，在6分频下启动电机，电机带2 N?m负载，定子侧电压85 V。馈入双馈之后每隔1 s切换一次转子侧变频器的频率，使变频器输出频率的分频数每隔1 s按6分频、7分频，8分频的顺序依次进行切换，双馈电机连续变频调速仿真实验波形如图7所示。

从图7中可以看出，以6分频进行双馈启动，在1 s时成功馈入双馈，速度稳定在1250 r/min，2 s时由6分频切换至7分频，速度升至1295 r/min后稳定运行，在3 s时再由7分频切换至8分频，速度升至1315 r/min后稳定运行。由图可知各频段切换前后电机转速变化平稳，转速及转矩震荡较小，从而说明在双馈电机进行变频调速的过程中，采用本文提出的频率间实时切换方式，各频段间的切换较为平滑，频率切换响应也较为迅速。

为更直观的反映实时切换方式下频率间切换的效果，下面将从U相电压波形的角度对切换过程进行分析。如图8为双馈电动机在变频调速过程中电压波形的变化情况。首先由图7（a）中电压波形可以看出在1 s时转子侧通入6分频变频电源馈入双馈，然后在2 s和3 s时，分别进行6分频至7分频以及7分频至8分频的切换，看以看出2 s和3 s两侧，电压波形的频率明显发生变化，且没有明显的波动或是震荡，图8（b）和图8（c）分别对频率切换时刻进行放大，由放大后的电压波形图可知，无论是6分频向7分频过渡或是7分频向8分频过渡，不同频段间均可以实现平滑切换，过渡过程几乎没有震荡，且在接到频率变化指令的下一刻即能按照新频率的触发时序对晶闸管进行触发，频率响应的实时性较高，能够较好的满足双馈调速系统对于调速性能的要求。

6  结论

本文提出了一种余弦交截法在线计算触发时刻的改进算法，使触发交点可以在线按点进行计算，基于此，本文着重论述了频率间实时切换方式下的连续变频策略，并通过搭建双馈调速系统模型对改进的在线化算法及实时连续变频策略进行了仿真验证，结果表明，改进后的在线化算法能够满足双馈电机对于交交变频器输出波形对称度、余弦度及平衡度的要求，且实时变频策略能实够现不同频率间实时切换的平滑过渡，并能够满足双馈电机对于连续变频调速性能的要求，可为双馈电动机实时变频调速提供一定的参考价值。

参考文献

[1]周玲华. 异步电动机的双馈调速—一种中压电动机经济可靠的节能调速方式[J]. 电力电子， 2004（2）： 40-43.

[2]谭兴国， 王艳， 王剑波. 交交变频器余弦交截法微机实现方法研究[J]. 电气開关， 2005（4）： 17-20.

[3]陈鑫， 杜庆楠， 乔美英， 鲁西坤. 矿井提升机变频调速控制策略的研究[J]. 计算机仿真， 2015（8）： 245-249.

[4]高曼曼， 杜庆楠. 双变量交交变频双馈电动机功率因数控制研究[J]. 工矿自动化， 2014（9）： 70-74.

[5]杜庆楠， 王新.晶闸管相控变流器及变频器的双变量相控理论[M]， 北京： 煤炭工业出版社， 2006.

[6]倪璐， 田力. 六脉波双变量交交变频调速系统的Matlab仿真[J]. 上海有色金属， 2014（4）： 165-169.

[7]高曼曼， 杜庆楠， 潘天文， 杨树德. 绕线电机启动状态到双馈状态过渡过程的研究[J]. 电气传动， 2012（12）： 23-26.

[8]张勇军， 潘月斗， 李华德.现代交流调速理论[M]. 北京： 机械工业出版社， 2014.

[9]姚剑， 朱桂平. 异步电动机软启动技术探讨[J]. 硫磷设计与粉体工程， 2004（3）： 34-38+53.

[10]杜庆楠， 王新， 陈立香. 相控变流器和变频器双变量控制理论的研究[J]. 煤炭学报， 2000（S1）： 154-157.

[11]曾聪， 杨世祥. 电动机软启动技术及应用[J]. 电气开关， 2005（6）： 25-27.