基于凸和非凸优化低秩矩估计的大数据处理算法
刘晓霞 王钰宁 陈 霞
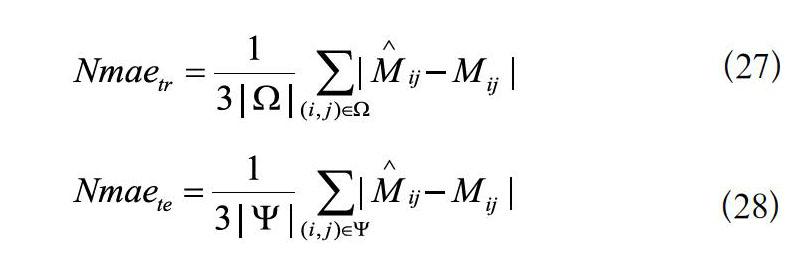
摘 要:针对大数据处理中存在的优化问题,提出一种基于凸和非凸优化低秩矩估计的大数据处理算法,并利用物联网采集与感知的大数据进行算法的实验验证与对比分析。在简单描述凸优化、非凸优化和低秩矩阵优化基础上,设计了基于凸和非凸优化低秩矩估计的大数据处理算法,并对算法收敛性进行了分析;然后利用物联网感知设备,进行数据感知与采集,然后利用所設计的算法进行对比实验。通过实验表明,本文算法在训练时和测试时,在归一化平均绝对误差和运行时间上,具有较好的结果。
关键词:凸优化;非凸优化;低秩矩阵;估计;大数据处理
中图分类号:TP309 文献标识码:A
Processing Algorithm for Big Data Based on Convex Optimization,Non-convex Optimization and Low-Rank Matrix Estimation
LIU Xiaoxia,WANG Yuning,CHEN Xia
(Department of Information Engineering,Sichuan Water Conservancy Vocational College,Chongzhou 611231,China)
Abstract:Aiming to the optimization problem in big data processing,a big data processing algorithm based on convex optimization,non-convex optimization and low rank matrix estimation is proposed,and the experimental verification and comparative analysis of the algorithm are carried out by means of the big data collected and perceived by Internet of Things.On the basis of convex optimization,non-convex optimization and low rank matrix optimization,the big data processing algorithm is designed and the convergence of the algorithm is analyzed.Then data perception and collection are performed by using the Internet of Things perception devices and the proposed algorithm is used to conduct comparative experiments.Experiments show that the proposed algorithm has good results in normalized mean absolute error and running time during training and testing.
Keywords:convex optimization;non-convex optimization;low rank matrix;estimation;big data processing
1 引言(Introduction)
各类数据信息形成的大规模高维数据正在以每年ZB(Zetta Byte,ZB)级海量递增,为处理和存储带来巨大的机遇和严峻的挑战。而各种数据的采集与处理过程中,几乎都是高维数据且相互关联,需要进行数据优化。而凸优化由于其在凸集、凸函数的结构和特性,具有不确定性,已应用于信号处理、生物信息学、机器学习和大数据等。
对于凸优化、非凸优化和低秩矩阵优化等,国内外研究者们进行了诸多研究,取得了一定成果。文献[1]对复杂网络关键节点选择问题进行研究,提出一种基于凸优化的维度不精确乘法器交替向量算法。文献[2]利用非凸优化理论研究航站间路径规划的编码问题,提出一种基于非凸优化的非连续时间的航站间约束满足的非凸路径规划编码算法。文献[3]对低秩矩阵优化中的全局最优性问题进行研究,分析一般目标函数下的最多矩阵的最小化问题。文献[4]利用随机方法对大规模矩阵进行低秩近似研究,提出了一个稀疏的正交变换矩阵来减少数据维数的算法。文献[5]用低秩矩阵完备的大规模通信估计。以上研究,将凸优化、非凸优化和低秩矩阵优化应用于不同场景,仅文献[6]利用凸优化、非凸优化和低秩序矩阵估计来处理大数据结构性问题。
综上,应用凸优化和非凸优化,结合低秩序矩阵优化的优越优化性能,研究大数据的处理算法,提出一种基于凸和非凸优化低秩矩估计的大数据处理算法,并利用物联网采集与感知的大数据进行算法的实验验证与对比分析。
2 相关优化方法(Related optimization method)
本部分,简单介绍凸优化、非凸优化和低秩矩阵优化的概念。
2.1 凸优化和非凸优化
凸优化的目标函数为凸函数,同时变量所属集合为凸集。在变量所属集合中的任意两点,连线得到的直线段,如直线段上的所有点,均分布于变量所属集合内,则该变量所属集合为凸集。即假定集合,若和,有:
成立,则称集合为凸集。假设给定集合为凸集,若使得:
成立,则称函数为定义在凸集上的凸函数。因此,若满足:
且为定义在(为凸集)上的凸函数,则该优化问题称为凸优化。
而不能直接用凸优化进行优化的问题即为非凸优化。而现实世界的大部分优化问题为非凸优化,非凸优化是可解决如机器学习、信号处理等,直接对非凸问题进行直接优化,得到全局最优解。
对应于凸优化之定义与描述,可形式化得到非凸优化的描述。如式(1)、(2)和(3)所示,若目标函数不是凸函数,则该问题为非凸优化;若变量中包含离散变量或0-1变量或整数变量,则该问题为非凸优化;约束条件,不是凸函数,则该问题为非凸优化。即假定集合,若和,有:
成立,则称集合为非凸集。假设给定集合为非凸集,若使得:
成立,则称函数为定义在非凸集上的非凸函数。因此,若满足:
且为定义在(为非凸集)上的非凸函数,则该优化问题称为非凸优化。
2.2 低秩矩阵优化
矩阵的秩描述矩阵行(列)向量极大无关组的个数。低秩矩阵是指给定矩阵的秩远小于矩阵的行数或列数。
对秩为的矩阵进行奇异值分解,可描述为:
其中,为对应的奇异值和奇异向量。由此,低秩矩阵的集合可描述为:
因此,低秩矩阵优化问题可形式化描述为:
其中,矩阵变量,函数为变量的损失函数;为矩阵的秩,作为正则化项描述,以確保矩阵的低秩特性;为平衡因子,以使损失函数和低秩间平衡。
低秩矩阵优化问题就转化为目标函数式(9)最小化问题,即通过优化算法,求解一个最优化矩阵,使得在给定平衡因子下,损失函数和矩阵的秩均为最小。
3 大数据处理算法(Big data processing algorithm)
本节将利用凸优化、非凸优化和低秩矩阵优化方法,设计一种基于凸优化和非凸优化低秩矩阵估计的大数据处理算法,并对算法的收敛性进行分析。
3.1 算法设计
对海量大数据进行处理,其处理问题大多为非凸问题,需要使用一定理论和方法进行凸问题转化。在快速有效地处理大数据方面,提出一种非凸正则化凸优化的低秩矩阵估计算法,并构建一种有效的解决方法来求解最优解。
给定缺少值的矩阵,其秩最小化的矩阵完备一般公式为:
其中,为矩阵中已知元素索引集合。因矩阵秩最小化问题为NP-hard(Non-deterministic Polynomial hard,NP-hard)问题,故需要用其他方法进行凸松弛优化,即:
通过广义奇异值阈值非凸逼近问题时,其较大奇异值为需保留的信息,而较小奇异值通常为零处罚函数的噪声信息。实际中,期望矩阵为近似低秩矩阵,并为秩最小化的矩阵。因此,引入弛豫函数进行正则化,以实现矩阵的最小化秩和核范数,对一个非凸正则化重构矩阵完备问题可描述为:
其中,;是具有的矩阵,否则;表示矩阵的Hadamard乘积。对式(12)增加较小的惩罚值并减少大值的惩罚,即对式(12)进行秩最小化和核范数的折中处理;假设,则式(12)可重新描述为:
其中,,显然是非凸函数;为正定矩阵。
对式(13)无法直接进行求解或优化,在此利用迭代加权最小二乘法对式(13)进行优化,其算法如算法1所示。
算法1 示意代码
Algorithm 1 Iterative Weighted Least Squares Optimization Algorithm
input:Incomplete data matrix
ouput:low rank matrix
init:initialize by
for (i=1;i<=n1;i++)
{
Eigenvalue split: (14)
Update by: (15)
Update by solving:
(16)
Convergence checking.
}
算法1迭代时,用当前加权矩阵进行更新,而后用当前更新的来更新。但算法1中的式(16)的求解式困难的,因此需要对其用拉格朗日函数进行辅助,即在忽略变量的条件下,得到:
其中,为拉格朗日乘数。对式(17)进行求导,并令其一阶导数为零,即:
其中,为正定矩阵,为可逆矩阵。
由上,得到:
对任意i,有:
其中,为对角矩阵。式(20)可改写为:
由于式(21)中,是一个奇异矩阵,导致式(21)的求解变得非常困难,因此由的结构特点,得到:
其中,为矩阵中非零元素的子向量;是对应的非奇异子矩阵。由此得到的最优解可通过求解得到。因此,的最优解即为的最优解。
3.2 算法收敛性分析
算法1中,在给定完备矩阵时,其迭代步长具有有界性。因在线性搜索过程中,迭代步长具有单调性,使得搜索条件式(14)得到满足,而且迭代步长不会无限增长,当迭代步长增长满足:
则搜索迭代停止。
定义1:若序列存在收敛的子序列,则该子序列收敛到的点称为累积点,其中。
定义2:若0属于在X*处次梯度集合,则称是式(10)中目标函数的稳定点。即:
其中,为函数在处的次梯度,且有
由上定义1和定义2可知,算法1产生的更新序列,使式(10)的目标函数单调下降,且序列所有累积点皆为稳定点。因此,算法1能够收敛于稳定点,且更新序列,为序列的任一累积点,则有:
即算法1的收敛速度为。
4 实验(Experiment)
4.1 实验数据采集
使用深圳亿道电子技术有限公司的物联网数据采集系统,如图1所示。
图1 实验数据采集系统
Fig.1 Experimental data acquisition system
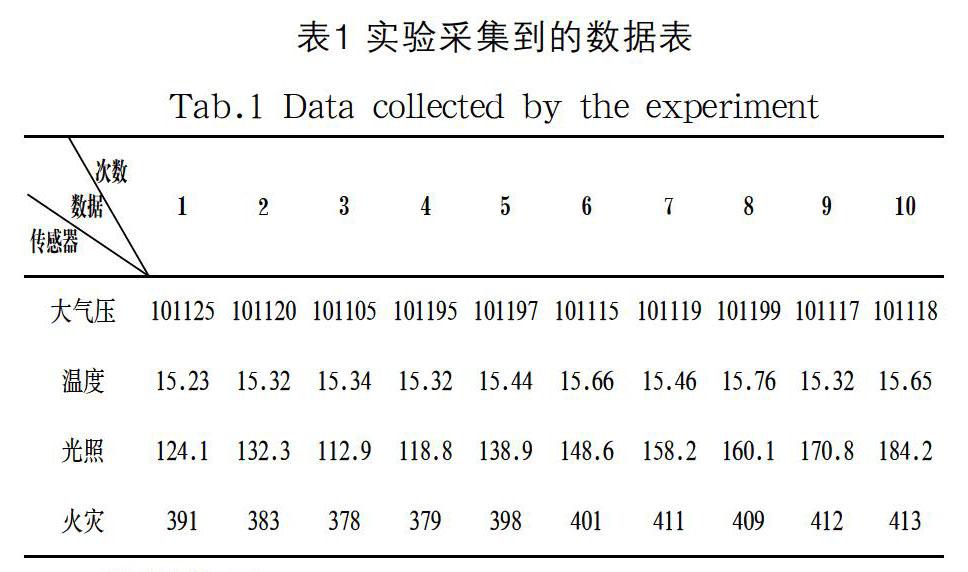
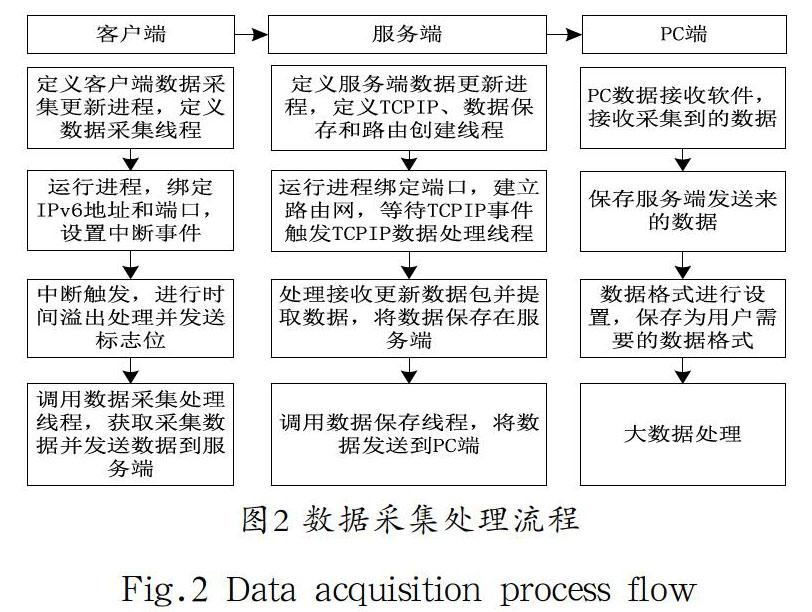
实验时,还需要建立实验采集系统软件,如图2所示,按照客户端、服务端和PC端来进行构建。所采集的数据有大气压、温度、光照和火灾,运行一段时间,采集到的数据如表1所示,每个感知数据的单位分别为帕斯卡、摄氏度、勒克斯和百万分之一(parts per million,ppm)。其中火灾传感器采用紫外感知CO/CO2的综合浓度。实验共采集50000次数据,由于篇幅限制,表1中仅给出10次。
图2 数据采集处理流程
Fig.2 Data acquisition process flow
4.2 数据处理
对上述感知到的数据进行初步处理,然后用s.dat存储。对s.dat里面的数据进行处理,划分为训练集sa.dat和测试集sat.dat。设表示s.dat中数据构成的不完整矩阵,并用表示s.dat中包含的所有可用数据的索引集。因此,和是的矩阵,每个。又设、分别描述训练和测试时不相交的数据集,且存在。
矩阵数据处理时,使用训练数据集作为矩阵完备输入算法1中,代替算法1的,由此用未得到的估计测试数据集,并将其存储于。对算法1,对少量数据进行调整,以便于对误差进行度量,故使用训练集和测试集上的归一化平均绝对误差(Normalized Mean Absolute Error,Nmae)进行数据的评判。
定义3若给定矩阵为矩阵完备,则定义训练矩阵和测试矩阵的Nmae分别为:
由定义3和矩阵的数据,在inteli76700处理器上,运行Apachespark模拟软件进行数据处理,并用文献[7]、[8]的算法对矩阵的数据进行处理,得到正则化处理比较曲线,如图3所示。
图3 数据处理参数正则化曲线
Fig.3 Data processing parameter regularization curve
图4 矩阵的数据处理Nmae和运行时间比较曲线
Fig.4 Matrix data processing Nmae and runtime comparison curve
由图3可知,运行同样字节数的矩阵M中的数据,在训练时返回的正则化矩阵的秩如图3(a)所示,由此可知,本文算法返回的秩较参比算法低;同样,图3(b)可知,在训练时和测试时进行正则化,得到的Nmae值,本文算法曲线变化比较平缓,仅开始随曲线变化较为陡峭,在矩阵M中的数据量达到5kB后,较参比算法而言,其变化趋势较为平缓稳定。由图4(a)可知,在训练时,随着矩阵M正则化得到的秩的增加,本文算法的Nmae变化趋近于线性,较参比算法而言,变化趋势较为平缓稳定。在测试时,随着秩的增加,本文算法得到的Nmae值在呈现下降趋势,其趋势接近于线性,而参比算法则波动较大。同样,由图4(b)可知,本文算法随着秩的增加,其运行时间增加比较平缓光滑,而参比算法无论在训练时还是测试时,其运行时间波动较大。
由上实验可知,本文提出的算法,无论时在训练时还是测试时,其Nmae值和运行时间,都具有较平稳的特性,且可近似于线性。
5 结论(Conclusion)
在大数据处理中存在的优化问题,提出一种基于凸和非凸优化低秩矩估计的大数据处理算法,并利用物联网采集与感知的大数据进行算法的实验验证与对比分析。在简单描述凸优化、非凸优化和低秩矩阵优化基础上,设计了基于凸和非凸优化低秩矩估计的大数据处理算法,并对算法收敛性进行了分析;然后利用物联网感知设备,进行数据感知与采集,然后利用所设计的算法进行对比实验。通过实验表明,本文算法在训练时和测试时,在归一化平均绝对误差和运行时间上,具有较好的结果。
参考文献(References)
[1] Ding Jie,Wen Changyun,Li Guoqi,et al.Key Nodes Selection in Controlling Complex Networks via Convex Optimization[J].IEEE Transactions on Cybernetics,2019,PP(99):1-12.10.1109/TCYB.2018.2888953.
[2] Arantes M D S,Toledo C F M,Williams B C,et al.Collision-Free Encoding for Chance-Constrained Nonconvex Path Planning[J].IEEE Transactions on Robotics,2019,35(2):433-448.
[3] Zhu Zhihui,Li Qiuwei,Tang Gongguo,et al.Global Optimality in Low-rank Matrix Optimization[J].IEEE Transactions on Signal Processing,2018,66(13):3614-3628.
[4] Hatamirad S,Pedram M M.Low-rank approximation of large-scale matrices via randomized methods[J].The Journal of Supercomputing,2018(74)830-844.
[5] 孙梦璐,唐起超.基于低秩矩阵完备的大规模MIMO系统信道估计研究[J].计算机应用研究,2018,35(6):247-250.
[6] Yudong C,Yuejie C.Harnessing Structures in Big Data via Guaranteed Low-Rank Matrix Estimation: Recent Theory and Fast Algorithms via Convex and Nonconvex Optimization[J].IEEE Signal Processing Magazine,2018,35(4):14-31.
[7] NieFeiping,Hu Zhanxuan,Li Xuelong.Matrix Completion Based on Non-convex Low Rank Approximation[J].IEEE Transactions on Image Processing,2019,28(5):2378-2388.
[8] Oh T H,Matsushita Y,Tai Y W,et al.Fast Randomized Singular Value Thresholding for Low-rank Optimization[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2015(99):376-391.
作者簡介:
刘晓霞(1976-),女,硕士,副教授.研究领域:大数据处理与应用,物联网技术.
王钰宁(1982-),女,本科,讲师.研究领域:大数据.
陈 霞(1971-),女,本科,副教授.高级工程师.研究领域:土木工程材料,施工应用,计算机技术应用.

