基于ISRCDKF的移动机器人同时定位与建图研究

齐咏生 孙作慧 李永亭 刘利强

(内蒙古工业大学电力学院， 呼和浩特 010080)

0 引言

随着人工智能技术的不断发展，移动机器人的自主定位已成为机器人研究领域的热点问题。同时定位和建图(Simultaneous localization and mapping，SLAM)[1]是指当移动机器人处于未知环境中时，如何凭借自身携带的外部传感器获取周围环境信息，增量式地构建地图，并且在已经构建好的地图上完成自主定位。这也是移动机器人实现智能导航的关键技术之一。在研究SLAM问题的过程中，移动机器人的自主定位与地图的构建密不可分，地图的构建依赖于机器人精确的位姿信息，而准确的地图又能促进机器人实现精确的自主定位。所以有学者将SLAM中定位与建图的关系比喻成“鸡和蛋”的关系[2]，两者相辅相成，任何一方都无法单独实现。

SLAM问题主要分为基于视觉的SLAM算法和基于激光雷达的SLAM算法两大类[3-4]。在视觉算法方面，有学者提出了RGB-D视觉SLAM算法[5-7]，该算法通过构建深度图像地图解决自主定位问题。与视觉传感器相比，激光雷达具有精度高、抗干扰能力强、夜间也能正常工作等优点，成为目前研究SLAM问题主要使用的外部传感器[8]。另外，SLAM问题中存在诸多不确定性因素，包括环境的不确定性、噪声的不确定性等，所以基于概率估计的方法成为研究SLAM问题的主流思想。该方法以贝叶斯滤波估计理论为基础，最早是通过扩展卡尔曼滤波(EKF)与SLAM算法结合[9-10]，形成了EKF-SLAM框架，该算法的计算复杂度为O(L2)，L为系统状态向量的维数。但是扩展卡尔曼滤波需要进行复杂的矩阵计算，难以满足实时性的需要，而且EKF在线性化时舍弃了系统的高阶项，导致误差变大。文献[11]提出了基于无迹卡尔曼滤波(UKF)的SLAM算法，计算复杂度为O(L3)。UKF是基于无迹变换(Unscented transform，UT)的一种滤波方法，不需要计算雅可比矩阵，复杂度相应降低。但是，随着系统状态向量的增加，无迹变换中采样点与中心点的距离越来越远，导致滤波发散。近年来，容积卡尔曼滤波(CKF)也被应用于SLAM中[12]，CKF根据容积变换实现系统状态的线性化，与UKF计算复杂度相同，而且具有更少的采样点，所以理论上精度更高。然而，随着系统状态向量的增加，CKF同样存在计算复杂的问题，无法从根本上减少算法的计算量。除此之外，还有研究提出了基于粒子滤波(Particle filter，PF)的SLAM算法[13-14]和经过改进的FastSLAM算法[15-19]。由于PF存在计算量大、粒子集容易退化、需要进行重采样等缺陷，故在SLAM的应用中还存在一些问题。

在中心差分卡尔曼滤波(Central difference Kalman filter，CDKF)的基础上，文献[20]提出了迭代中心差分卡尔曼滤波算法，该算法通过Gauss-Newton迭代方法进行观测更新，在一定程度上提高了算法的精度。但是该算法在状态更新中传递的是整个协方差矩阵，无法解决计算复杂的问题，而且Gauss-Newton迭代方法在处理该问题时性能不够稳定。文献[21]提出了自适应平方根中心差分卡尔曼滤波算法，该算法可以根据输入的状态量自行调整参数性能，能够在一定程度上克服噪声的影响。但是随着计算步骤的增加，由于没有观测状态的矫正，该算法的估计误差逐渐增大，从而使系统失去稳定性。

针对目前的SLAM算法普遍存在定位精度不高或计算复杂的问题，本文提出一种基于迭代平方根中心差分卡尔曼滤波的SLAM算法，简称为ISRCDKF-SLAM算法，计算复杂度为O(L3)。该算法使用中心差分变换原理，通过Stirling插值公式替代泰勒公式进行因式分解[22]，降低复杂度；将平方根滤波理论引入算法中，通过传递噪声协方差矩阵的平方根矩阵减少算法计算量；在迭代观测更新的过程中，使用L-M方法引入调节参数，通过修正协方差矩阵增强算法的稳定性。通过仿真测试实验和基于实物平台的现场实验对算法的有效性和时间性能进行验证。

1 算法原理

1.1 SLAM问题的概率学描述

图1 SLAM问题的概率模型Fig.1 Probabilistic model of SLAM problem

因为SLAM问题遵循马尔可夫模型，所以可以根据车辆当前时刻的位姿信息、控制信息和环境信息将其转换为求下一时刻机器人位姿和环境特征地图的联合后验概率问题[23]，概率模型如图1所示。图中，xt为t时刻机器人的状态向量；yt为t时刻的观测向量；ut为t时刻的控制向量；m为路标特征点。

假设环境中存在n个可观测的路标特征点，那么M={m1,…，mi,…，mn}表示环境地图信息。根据以上参数，可以推算出t时刻机器人位姿信息和环境特征地图的后验概率分布为

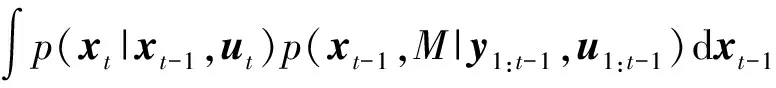
(1)

式中y1:t——初始时刻到t时刻的观测信息

u1:t——初始时刻到t时刻的控制信息

p(yt|xt,M)——传感器观测概率模型

p(xt|xt-1,ut)——机器人运动概率模型

p(xt,M|y1:t,u1:t)——t时刻的后验分布

p(xt-1,M|y1:t-1,u1:t-1)——t-1时刻的后验分布

η——归一化系数

1.2 中心差分变换

中心差分变换主要是利用Stirling插值公式来解决系统中的非线性问题。因为SLAM本身是一个比较复杂的非线性系统，所以中心差分变换使用多项式逼近非线性方程导数的方法替代了泰勒公式等复杂的运算，便于求解均值和协方差等统计量，可以从理论上减少算法的复杂度。中心差分的一阶和二阶导数公式为

(2)

(3)

h——中心差分半步长

δx——零均值的随机变量

2 迭代平方根中心差分卡尔曼滤波SLAM算法

首先，使用一组加权的采样点来近似系统的状态分布，以解决非线性系统的概率估计问题。其次，将平方根滤波理论引入到算法中，同时在观测更新中使用L-M方法优化迭代过程，最终，形成了迭代平方根中心差分卡尔曼滤波来处理上述的SLAM问题。

假设移动机器人的状态方程和观测方程分别为

xt=f(xt-1,ut-1)+w

(4)

yt=h(xt)+v

(5)

式中xt-1——机器人t-1时刻的状态向量

ut-1——机器人t-1时刻的控制向量

yt——机器人t时刻的观测向量

w——服从于N(0,Q)的高斯白噪声

Q——系统噪声协方差矩阵

v——服从于N(0,R)的高斯白噪声

R——观测噪声协方差矩阵

本文提出的ISRCDKF-SLAM算法由状态预测过程和迭代观测更新过程组成，具体算法步骤描述如下。

2.1 系统初始化

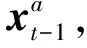
(6)

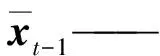
E()——求均值函数

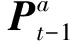
(7)

式中 chol()——乔里斯基(Cholesky)分解函数，又称平方根法，可以求得矩阵的平方根矩阵

2.2 状态预测

(8)

式中ξt-1——t-1时刻的Sigma点，共2L+1个

每个Sigma点对应的权值公式为

(9)

ξt|t-1=f(ξt-1)

(10)

(11)

式中ξt|t-1——Sigma点ξt-1沿非线性函数f(·)传播得到的变量

ξi,t|t-1——变量ξt|t-1的第i列数据

(12)

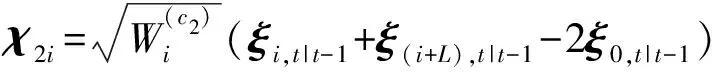
(13)

(14)

式中χ1i——一阶序列权值下的状态量

χ2i——二阶序列权值下的状态量

qr()——矩阵的QR分解函数

2.3 迭代观测更新

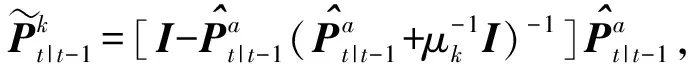
在观测更新开始前首先定义初始值ψ1作为线性化参考点，其值等价于当前时刻由状态预测得到的状态均值估计量，公式为

(15)

参数初始化后，开始进行迭代更新，具体计算步骤为

Fork=1:j

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

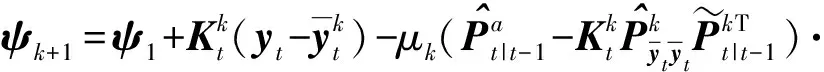
(25)

End for

式中μk——L-M方法的参数，取0.1

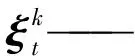
β1i——一阶序列权值下的观测变量

β2i——二阶序列权值下的观测变量

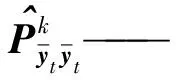
2.4 状态增广

当k=j时，迭代过程终止，可以得到t时刻经过迭代更新后状态矩阵的均值为

(26)

式中j——最大迭代数，均衡考虑实时性与精确性的要求，本算法中j=3

那么，t时刻状态的协方差的平方根矩阵公式为

(27)

式中 cholupdate()——乔里斯基因子更新函数

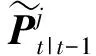
通过重复进行2.1～2.4节的步骤，最终可以实现基于ISRCDKF的SLAM算法在移动机器人中的应用。

3 仿真实验与分析

3.1 建模

移动机器人运动过程和传感器观测过程都需要适当建模才能完成算法的实现。本文参照文献[9]的SLAM模型，分别建立了简化后前轮可以转向的车辆运动学模型和传感器观测模型。

机器人的运动学模型为

(28)

式中xx(t)、xy(t)、β(t)——t时刻的状态变量，车辆在x、y轴坐标值和朝向角

ΔT——时间间隔

Vt——t时刻车辆速度

αt——t时刻车辆前轮转向角

Ld——前轴心与后轴心之间的距离

观测模型为距离-角度模型，用极坐标表示，公式为

(29)

式中x0、y0、β0——车辆当前的状态参数

xi、yi——第i个特征点的全局坐标值

ρi——环境特征点与机器人的距离

θi——环境特征点与机器人的夹角

3.2 仿真实验

实验使用的是内存为8 GB、主频为2.20 GHz的Intel(R)Core(TM)i5-5200四核处理器便携式计算机，程序运行环境为Matlab 2014a。

仿真实验是在澳大利亚悉尼大学野外机器人中心(ACFR)提供的开源SLAM算法仿真器上进行的。仿真环境设定在一个长、宽为250 m×200 m的室外环境中，并且在该环境中放置了17个路径点，用于确定机器人的运行路径，同时放置了35个环境特征点作为移动机器人SLAM过程中的外部环境观测信息，具体的仿真环境如图2所示。

在图2中，“*”表示环境特征点，虚线表示机器人理想的行驶路径。设定的实验参数有：机器人行驶速度4 m/s，速度的控制噪声0.2 m/s，激光雷达的观测距离25 m，观测距离噪声0.1 m。实验的具体过程为：机器人首先从原点(0,0)出发，按照参考路径和环境特征点信息进行SLAM运算，逆时针行走两圈后停止。实验中，将提出的ISRCDKF-SLAM算法分别同EKF-SLAM、UKF-SLAM、CKF-SLAM算法进行对比，并对实验数据进行比较分析。不同算法仿真结果如图3所示。

图2 仿真环境图Fig.2 Diagram of simulation environment

图3中，实线表示机器人实际行走的SLAM路径，圆圈表示对环境特征点的匹配精确度。通过对4种算法的结果比较分析可以看出，在算法初始阶段机器人行驶路径的误差都不大。但随着环境信息增多，EKF-SLAM出现较大的误差，这是因为EKF在数据关联中出现了错误，导致第2圈的行驶路径彻底发散。ISRCDKF-SLAM算法与UKF-SLAM、CKF-SLAM相比，实际路径与原始路径偏移量最小，这是因为通过迭代观测更新，会减少样本处理时的线性化误差，使机器人的位姿估计更加准确。

图3 不同算法仿真结果对比Fig.3 Comparison of simulation results of different algorithms

算法的性能估计标准采用均方根误差(Root mean square error，RMSE)衡量，计算公式为

(30)

式中T——运行时间

xk、yk——k时刻的理想位置坐标值

4种算法的均方根误差和仿真时间如图4所示。分析数据可知，本文提出的ISRCDKF-SLAM算法与EKF-SLAM、UKF-SLAM、CKF-SLAM算法相比，均方根误差分别降低了47.3%、32.7%和25.0%，验证了SLAM过程中定位更加准确。通过仿真时间对比，可以得出ISRCDKF-SLAM算法耗时仅次于EKF-SLAM，在算法实时性上也具有一定的优势。

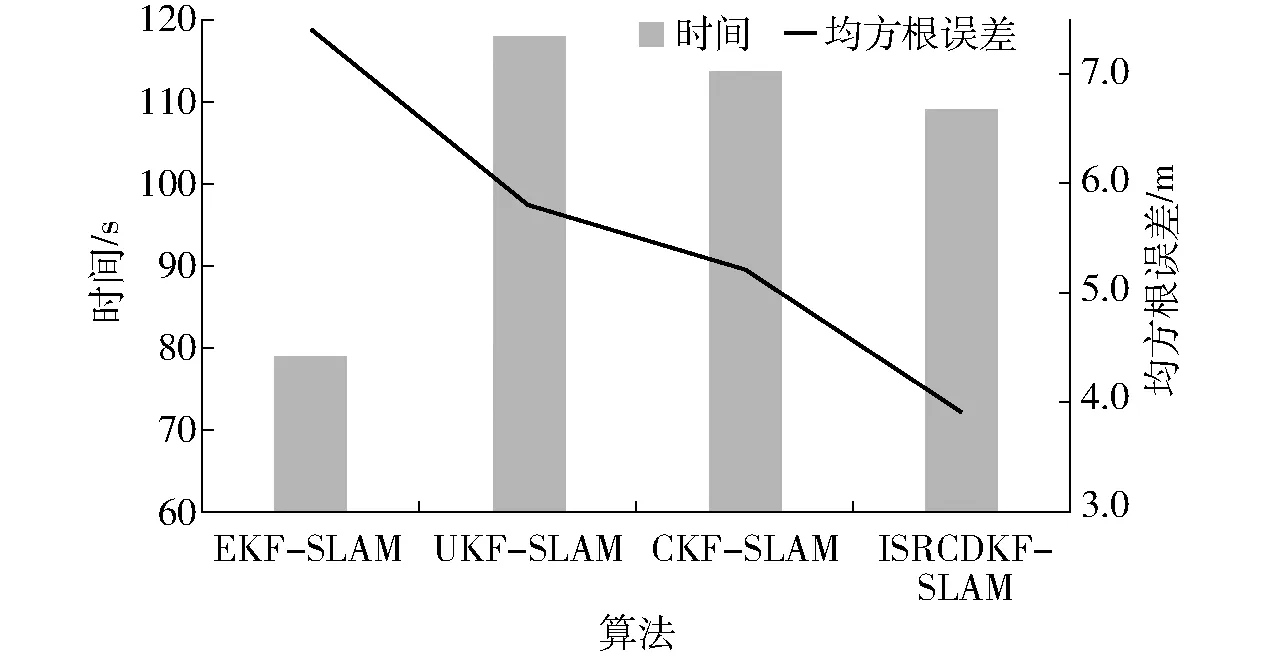
图4 不同算法时间和均方根误差对比Fig.4 Comparison of time and RMSE of different algorithm

3.3 “Car Park-dataset”停车场实验

“Car Park-dataset”停车场数据集是SLAM的标准数据集之一，该数据是在悉尼大学的一处面积为45 m×30 m的停车场环境中采集而来的。首先人为的在停车场中放置15个人工路标当做环境特征点，然后驾驶四轮皮卡型汽车(移动机器人)围绕路标低速行驶约2 min，采集到的数据包括：后轮线速度和前轮转向角、路标位置信息、经纬度信息。由GPS传感器测得的车辆真实轨迹如图5所示。

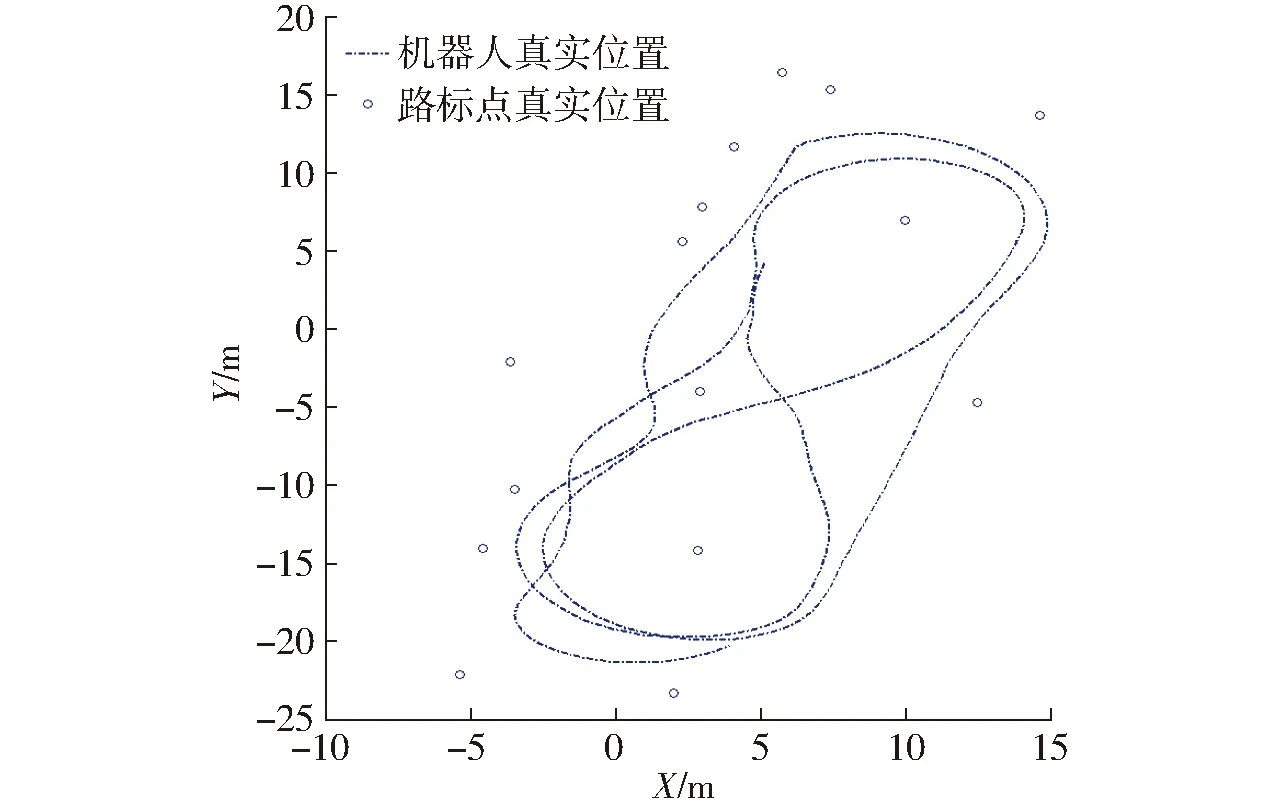
图5 车辆真实轨迹图Fig.5 Diagram of vehicle real trajectory

通过停车场数据集实验，进一步验证ISRCDKF-SLAM算法的有效性。实验中，设置机器人速度噪声为0.5 m/s，车轮转向噪声为1°；传感器观测噪声为0.2 m，观测角度噪声为1.5°。分别采用ISRCDKF-SLAM算法与UKF-SLAM、CKF-SLAM算法(此处只比较相同复杂度的SLAM算法)进行仿真比较，使用式(30)所示的算法性能估计标准进行数据分析。3种算法的车辆位置误差如图6所示，特征点位置误差如图7所示。

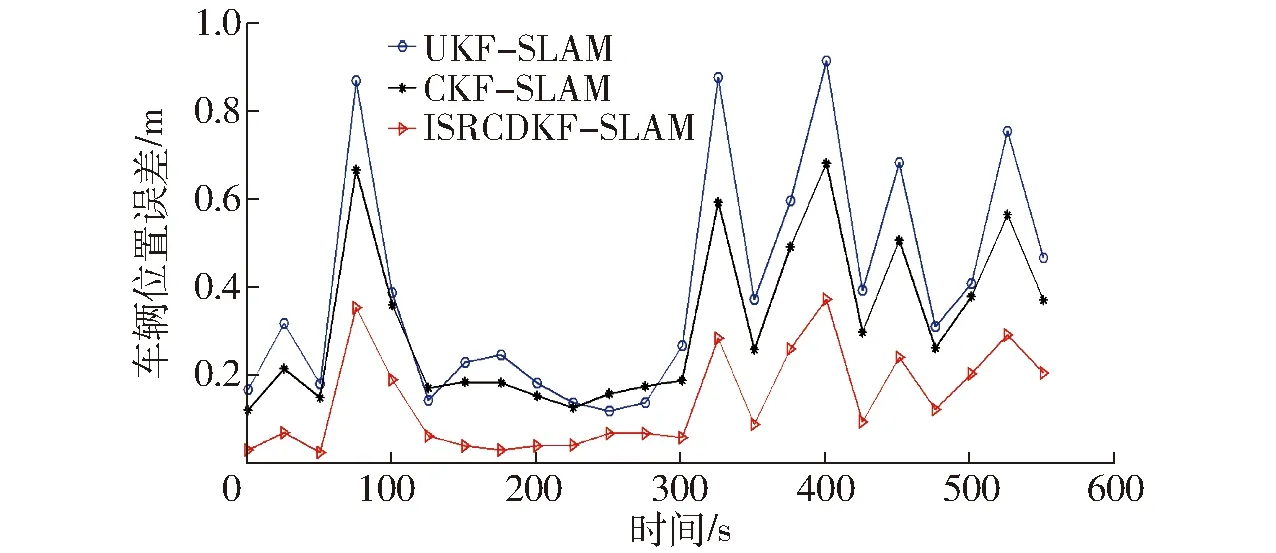
图6 车辆位置误差Fig.6 Vehicle position error

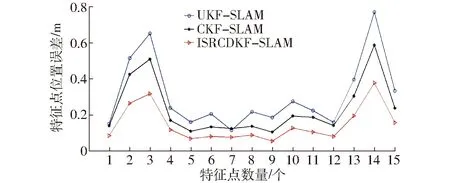
图7 特征点位置误差Fig.7 Characteristic point position error

从图6中可以看出，UKF-SLAM算法的车辆位置误差大多数情况下处于最大位置，因为无迹变换在线性化时产生了较大误差。ISRCDKF-SLAM算法因为在观测更新过程中使用了迭代更新，而且在整个滤波过程中都传递协方差矩阵的平方根因子，所以车辆的位置误差始终最低。图7中，UKF-SLAM算法的特征点位置误差比其他两种算法的误差值稍大，ISRCDKF-SLAM算法的特征点位置误差最小。

表1为分别独立运行30次仿真实验后，得到的3种算法的平均运行时间和平均误差最大值。分析表中数据可以看出本文提出的ISRCDKF-SLAM算法的误差明显低于其他两种算法，而且与UKF-SLAM和CKF-SLAM算法相比，新算法的运行时间分别减少了15.1%和10.8%。但是由于需要迭代观测更新，在算法运行时间上优势不是太明显，这需要以后对迭代算法做进一步的优化。

表1 不同算法的误差与时间对比Tab.1 Error and time comparison of different algorithms

4 实物平台实验与分析

为了更近一步验证算法的有效性，本文搭建了四轮移动机器人平台，如图8所示。该机器人的主控板为树莓派3B，搭载了频率为1.2 GHz的64位四核ARM处理器；底盘由STM32单片机控制电机的运动；使用的激光雷达为思岚公司开发的2D雷达RPLIDAR A2。同时，机器人还安装有IMU和编码器等内部传感器。

图8 移动机器人平台Fig.8 Photos of mobile robot platform1.激光雷达 2. 12 V锂电池 3.树莓派 4.单片机 5.电源转接板

使用机器人操作系统(Robot operating system，ROS)作为软件开发平台，安装在基于树莓派的Ubuntu 16.04 Linux系统下。在ROS自带的Hector_mapping程序包的基础上，分别将UKF、CKF和本文提出的ISRCDKF滤波算法移植到该程序中，形成了UKF-SLAM算法、CKF-SLAM算法和ISRCDKF-SLAM算法。在相同的实验场景与参数配置下，分别对这3种算法进行对比实验。

4.1 走廊实验

首先在实验室外面的走廊进行建图实验，环境包括走廊和与走廊边缘呈直角的拐角区域，实景拍摄如图9所示。

图9 走廊实验环境Fig.9 Photos of corridor experimental environment

配置好移动机器人后，将机器人放置在走廊的一端作为初始位置，然后将计算机与机器人连在同一个局域网下。计算机远程打开终端启动程序包，运行Rviz软件接收各个节点发布的话题进行实时的图形化显示，现场实验如图10所示。

图10 现场实验初始界面Fig.10 Field experiment initial interface

启动SLAM程序，让移动机器人绕走廊环境行驶一圈后回到起始点，可以构建出走廊的环境地图。图11为不同的算法下构建的地图，图中左上角为局部放大图。

图11 不同算法构建的地图对比Fig.11 Comparison of maps constructed by different algorithms1.拐角 2.楼梯口 3.洗刷间 4.立柱 5.走廊

通过对3种算法的建图情况对比可以得出前2种SLAM算法构建的地图在走廊拐角处的数据关联发生错误，均出现了误匹配的现象，导致后面的建图局部出现失真，走廊整体呈弯曲的状态，基于ISRCDKF-SLAM算法构建的地图优于其他两种算法。

在建图过程完成后，通过获取激光雷达和机器人内部传感器的参数可以估算出建图过程中的平均直线误差和角度误差，并且能够得到算法运行时间。分别对3种算法在走廊环境中做了3次建图实验，通过式(30)所示的均方根误差法对上述两组参数作对比，得到的数据如表2所示。通过分析表中数据可以直观看出ISRCDKF-SLAM算法在地图的构建上误差更低，且算法平均耗时最短。

4.2 室内实验

由于走廊是一个简单的环境，特征点相对较少，为了完成不同环境下的SLAM建图，接下来在相对

表2 走廊实验数据Tab.2 Corridor experimental data

复杂并且有回环的室内进行SLAM研究。实验环境如图12所示，左图中依次排放着3个桌子，桌子基本在同一水平线上，右图放置了一个紧贴着墙的壁橱。

本次实验使用了ISRCDKF-SLAM与CKF-SLAM(UKF-SLAM与CKF-SLAM效果相当，此处未给出对比结果)2种算法进行对比实验。控制机器人在室内走完一圈后，算法构建的地图如图13所示。

图12 室内实验环境Fig.12 Indoor experimental environment

图13 构建的室内地图Fig.13 Built laboratory map1.桌子 2.桌底 3.壁橱 4.拐角

通过对2种算法构建的地图进行比对测量，得出改进后算法构建的地图长宽方向的误差更低一些，整体精度更高。同时在地图上可以看出，算法改进后地图中的直角特征更为准确，桌子的排列更加整齐。同样使用均方根误差法，将这两种算法在室内环境下分别独立执行了3次建图实验，通过传感器数据估算的平均直线误差和角度误差如表3所示。通过数据得出在特征点较多的环境下，新提出的算法依然能够进行更加精准的自定位与地图构建。

表3 室内实验数据误差Tab.3 Indoor environmental data error

5 结束语

针对目前移动机器人在同时定位和建图中存在的状态精度不高、稳定性差等问题，在滤波理论的基础上，提出了一种基于ISRCDKF的SLAM自主定位算法。该算法使用中心差分变换处理SLAM的非线性问题，在滤波更新过程中通过直接传递协方差矩阵的平方根因子减少算法的复杂度，同时在迭代观测更新过程中使用L-M优化方法引入调节参数实时修正协方差矩阵。仿真实验表明，与传统的EKF-SLAM、UKF-SLAM、CKF-SLAM算法相比，ISRCDKF-SLAM算法在自主定位与地图构建方面的均方根误差分别降低了47.3%、32.7%和25.0%。与相同计算复杂度的UKF-SLAM算法和CKF-SLAM算法相比，新算法的运行时间分别减少了15.1%和10.8%。搭建了移动机器人实物平台进一步验证了该算法的有效性，从而为移动机器人SLAM问题的研究提供了一个新的思路。