基于改进CEEMD的管道多点泄漏定位分析

邢志祥，朱一龙，郝永梅，蒋军成，盛 璘，杨 健，杨 克

(1.常州大学环境与安全工程学院，江苏 常州 213164；2.常州港华燃气有限公司，江苏 常州 213161)

城市管道在长期使用过程中，因受内外腐蚀等多种因素的影响而容易引发泄漏[1-2]，尤其是早期发生的微小泄漏，由于其泄漏孔径小、泄漏流量小等特点，导致微小泄漏难以通过视觉、听觉和管道检测系统捕捉。实际工况中，一段被测管道往往存在多个泄漏源，而多点泄漏具有信号干扰大、信号包含内容多等特点，导致多点泄漏信号难以提取、定位误差大，给实际检测带来诸多问题[3]。

近年来，国内外学者针对管道泄漏检测和定位做了大量的研究，如章冲[4]利用光纤检测法对管道多点泄漏进行了定位检测，但该法造价昂贵、定位精度较低；李玉星等[5]基于希尔伯特黄变换与盲源分离技术对管道泄漏声波进行提取、分离、定位，但其泄漏孔径为0.6 mm，并不适用于微小泄漏的研究；杨凯[6]利用改进的CEEMD(互补集合经验模态分解)方法对地震含噪信号进行去噪，解决了模态混叠问题并提高了信噪比，但未对分解产生的无效冗余分量进行剔除，其精度有待提高；Ozevin等[7]基于声发射和几何连通法，由交叉相关函数计算出多维管网泄漏的位置，但该研究仅在理论上得到证实，并未出现实施案例；Scholey等[8]利用传感器间距和波速依赖性对管道泄漏信号进行时间差计算，从而产生定位结果，但该法需要大量弹性波训练点；Mostafapour等[9]利用小波变换和交叉时间频谱理论，对管道声发射信号进行了精确定位，但无法做到多点泄漏定位。

以上研究虽然不同程度地解决了声发射信号的处理和定位问题，但对于城市管道的微小泄漏，尤其是多点微小泄漏，尚未形成较为可靠、完善的定位技术[10]。因此，本文在管道泄漏定位现有研究成果的基础上，基于管道泄漏声波理论，提出了一种基于改进CEEMD的城市管道多点泄漏定位分析新方法，以解决多点泄漏源信号的提取，并进一步精确定位。

1 改进的CEEMD方法

1.1 CEEMD方法原理

CEEMD是在经验模态分解(Empirical Mode Decomposition，EMD)基础上发展起来的一种信号分解方法，然而EMD不稳定且存在模态混叠问题[11]，于是Wu等[12]提出了集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法，利用高斯白噪声频谱均匀分布统计特性加至信号中，使得信号在不同尺度上具有连续性。EEMD方法虽解决了模态混叠问题，但却不能完全中和人为添加的白噪声，文献[13]在EEMD方法的基础上，将互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)方法应用信号分析中，减小了EEMD人为添加白噪声引起的重构误差。CEEMD方法的具体算法步骤如下[14]：

定义运算符号Ej(·)为EMD分解的第j个固有模态函数，ωi(t)(i=1,2,…,n)是单位方差为零均值的高斯白噪声，εk是每个阶段设定的信噪比系数。

(1) 首先对原始信号x(t)加入高斯白噪声ωi(t)，对目标信号x(t)+ε0ωi(t)进行n次EMD分解，获得第一个固有模态函数IMF1(t):

(1)

(2) 然后计算得到一阶残差r1(t):

r1(t)=x(t)-IMF1(t)

(2)

(3) 在一阶残差r1(t)中添加白噪声信号，构造信号r1(t)+ε1E1[ωi(t)]并再次进行分解，获得第二个固有模态函数IMF2(t):

(3)

(4) 以此类推，计算第k阶残差rk(t)(k=2,3,…,K):

rk(t)=r(k-1)(t)-IMFk(t)

(4)

(5) 再继续分解rk(t)+εkEk[ωi(t)]，得到第k+1个固有模态函数分量为

(5)

(6) 继续分解直至满足结束条件，即残差极值最多不超过两个，否则返回至步骤(4)～(5)中进行计算，最终目标信号x(t)可表示为

(6)

1.2 改进的CEEMD方法

CEEMD方法不仅解决了EMD引起的模态混叠等问题，而且在保证EEMD分解效果的前提下，还减小了分解过程中人为添加白噪声不能完全中合的缺陷。但CEEMD方法仍然存在两个问题:其一是分解后的信号模态中仍残留随机噪声；二是存冗余分量。

通过引用信号局部均值算子M(·)改进CEEMD方法分解过程，对局部均值直接进行估算，既提高了运算效率，又可分解得到冗余分量。冗余分量的计算过程可表示为

(7)

式中：r(t)表示冗余分量，k=1,2，…，n;M(·)表示产生信号局部均值的算子；E(·)表示产生第k个模态的算子；ω是单位方差为零均值的高斯白噪声；ε为每个阶段设定的信噪比系数。

同时，通过在CEEMD过程中编译带通滤波器代码，能够把噪声集中在较少的IMF分量上，由此，通过改进的CEEMD方法计算整体局部均值，最终可使信号分解结果为噪声分量、有效信号分量和冗余分量，即：

(8)

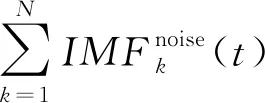
1.3 互相关峭度理论

互相关函数是描述随机信号m(t)、n(t)在任意两个不同时刻t1、t2的取值之间相关程度的函数，互相关函数给出了频域内两个信号是否相关的判断指标，通过联系两个信号的互谱与自谱，可精确判定输出信号来自于输入信号[15]的相关程度，其相关系数的计算公式为

(9)

目前在统计学界，相关系数大小所表示的意义尚未形成统一观点，但通常按表1确定[16]。

表1 相关系数-相关程度表示[16]Table 1 Correlation coefficient-correlation degree representation

根据互相关峭度理论，通过计算各阶IMF分量与原始粗定位信号的相关程度，进一步验证改进的CEEMD方法的分解效果。

2 基于改进CEEMD的管道多点泄漏定位

2.1 基于改进CEEMD的管道多点泄漏定位模型建立

将改进的CEEMD方法结合互相关峭度理论和盲源分离技术，建立了管道多点泄漏定位模型，见图1。

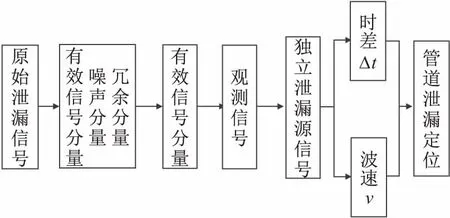
图1 管道多点泄漏定位模型Fig.1 Pipeline multi-point leakage location model

通过改进的CEEMD方法可将管道泄漏原始信号直接分解为包含噪声分量、有效信号分量和冗余分量三种成分的IMF分量；经互相关峭度理论对提取的有效信号分量进行验证，确保改进的CEEMD方法的分解效果；再结合小波重构和盲源分离技术，获得独立泄漏源信号；最后通过管道声发射时差定位公式，获得管道泄漏的精确定位。

2.2 基于改进CEEMD的管道多点泄漏定位计算步骤

对于管道多点泄漏，上、下游传感器接收到的信号为混合粗定位信号，基于改进的CEEMD方法对管道多点泄漏进行信号提取和定位的计算步骤如下：

(1) 通过管道多点泄漏模拟试验获取原始粗定位信号x(t)。

(2) 采用改进的CEEMD方法分解原始信号x(t)，获得IMF有效信号分量。

(3) 根据互相关峭度理论，验证有效信号来自于真实信号的相关程度。

(4) 对验证的有效信号分量进行小波软阈值去噪，获得观测信号s(t)。

(5) 利用Fast ICA算法对混合的观测信号s(t)进行盲源分离，获得独立泄漏源信号h(t)，并计算独立泄漏源的信号定位时差Δt。

(6) 计算管道泄漏点的位置x。

3 实例应用与分析

3.1 金属管道多点泄漏模拟试验

图2 管道泄漏模拟试验系统图Fig.2 Pipeline leakage simulation system

试验管道长度为50 m，管道材质为钢材，管道规格为DN150，运输介质为压缩空气，见图2。1号上游传感器位于零点处，2号下游传感器位于40 m处，距离1号传感器16 m和30 m处设有2.0 mm的泄漏孔，见图3。本试验分别在0.3 MPa、0.2 MPa、0.1 MPa压力下进行，共做3组试验，每组试验进行4次，以获得泄漏信号的原始数据。

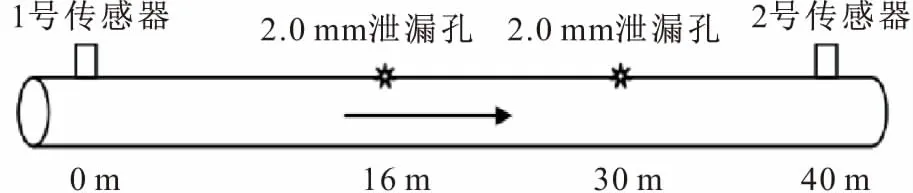
图3 管道泄漏模拟试验示意图Fig.3 Schematic diagram of pipeline leakage simulation test

根据管道声发射检测原理获取试验数据，随机提取12个峰值相对集中且幅值较高的泄漏信号原始数据作为后续处理原始粗定位信号x(t)，见表2。

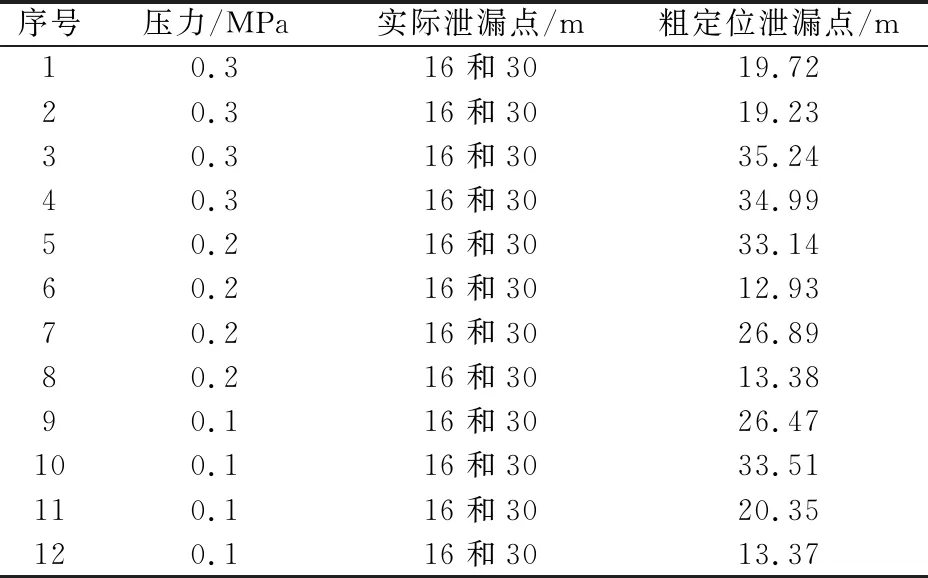
表2 管道两点泄漏的原始数据Table 2 Pipeline two-point leakage original data

3.2 管道多点泄漏分析定位处理

由表2可知，管道泄漏粗定位存在较大误差，需进一步进行分析处理。本文随机选取表2中序号为1的数据进行具体计算。

3.2.1 改进的CEEMD方法对原始信号进行分解

将表2中序号为1的数据上游通道的原始粗定位信号作为CEEMD的输入量进行分解，其分解结果见图4。

图4 改进的CEEMD对上游原始信号的处理结果图Fig.4 Processing result graph of upstream original signal by improved CEEMD

由图4可见，上游原始信号被自适应地分解为11阶IMF分量。其中，噪声分量主要集中在前3阶IMF分量；4～7阶IMF分量保持泄漏信号的幅值特性，属于有效泄漏信号分量；8～11阶IMF分量的信号特性逐渐消失，属于冗余分量。因此，本文选择4～7阶IMF有效信号分量进行提取。

3.2.2 互相关峭度验证

根据前述的互相关峭度理论，可对改进的CEEMD方法的分解结果进行验证：对所有分解得到的IMF分量，求其本身与原始粗定位信号x(t)的互相关程度，将相关性为微相关的信号分量认定为噪声分量和冗余分量，通过对比微相关信号分量与改进的CEEMD方法分解得到的噪声分量和冗余分量是否一致，以进一步验证改进的CEEMD方法的有效性。本文选取第4阶清晰度较高的IMF分量进行互相关系数计算，其计算结果见图5。上游共11阶IMF分量的互相关系数的计算结果汇总于图6。

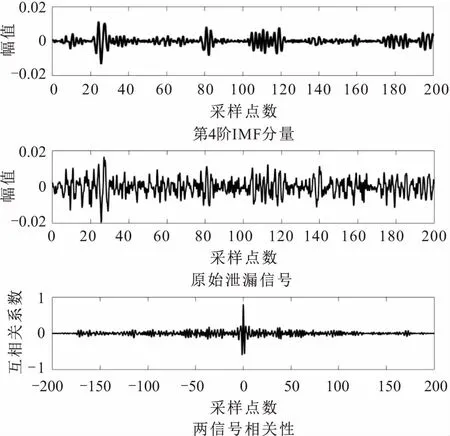
图5 第4阶IMF互相关系数的计算结果Fig.5 Calculation result coefficient of the forth-order IMF cross-correlation

图6 上游各阶IMF分量互相关系数的计算结果Fig.6 Calculation results of cross-correlation coefficients of upstream component IMF '

由图6可见，前3阶IMF分量的互相关系数在0.3以下，互相关系数较低；4～6阶IMF分量的互相关系数较高，均高于0.8，尤其第4阶IMF分量的互相关系数几乎接近于1；第7阶IMF分量的互相关系数骤降至0.3左右；8～11阶IMF分量均与原始泄漏信号无相关性，其互相关系数几乎为0。该验证结果与改进的CEEMD方法的计算结果基本一致，从而证明了改进的CEEMD方法的有效性。

3.2.3 小波软阈值去噪

改进的CEEMD方法分解出来的噪声主要是来自于环境、介质等的噪声，而有效信号分量中还含有人为添加的白噪声，需要借助小波软阈值去噪。针对管道声发射信号的特性，采用可实现离散小波变换的小波基函数[17]，即sym8函数；分解尺度由泄漏声波中含有的信号种类数决定，即分解尺度N取3。对4～7阶IMF真实信号分量进行去噪处理，并选取第4阶清晰度较高的IMF分量进行小波软阈值去噪计算结果展示，见图7。

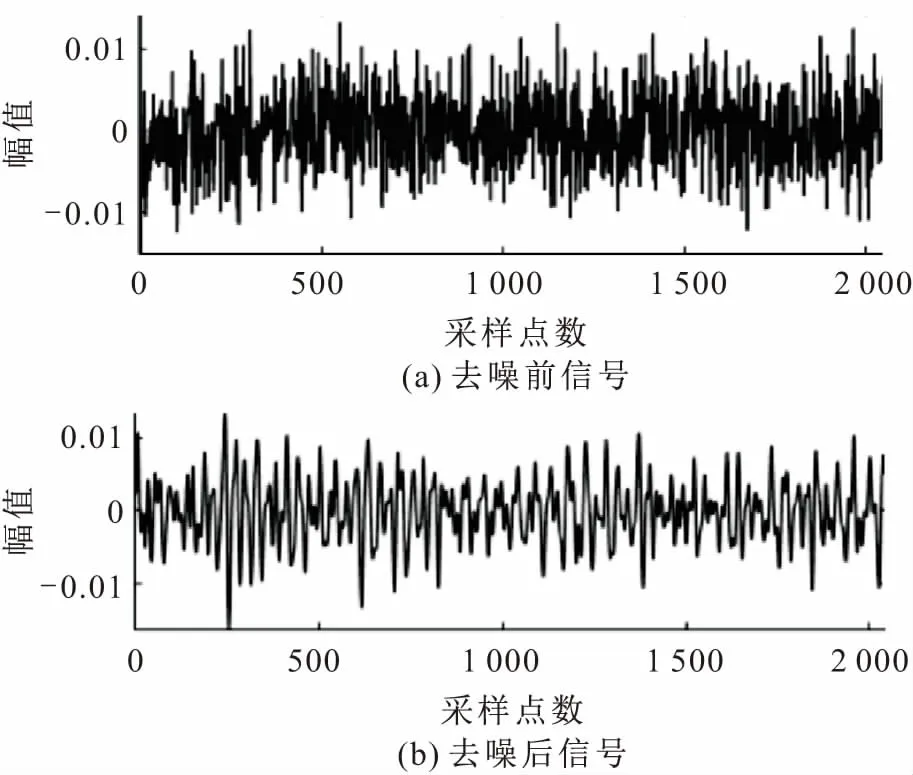
图7 第4阶IMF分量小波软阈值去噪的计算结果Fig.7 Calculation results of wavelet soft threshold denoising of the forth-order IMF component

影响小波去噪效果的因素很多，选择不同小波基、阈值、分解尺度，其去噪效果都不尽相同。因此，本文采用信噪比(SNR)和均方误差(RMSE)指标对小波去噪的效果进行衡量，小波去噪前后指标的对比结果见，表3。

表3 小波去噪前后指标的对比Table 3 Comparison before and after wavelet denoising

由表3可知，去噪前后的SNR和RMSE指标均发生了变化，具体来说，去噪后信号的SNR指标变大，RMSE指标变小，表示小波软阈值去噪有一定的效果。另外，由图7可见，去噪后信号的平滑度明显增加，噪声干扰明显减少。对去噪后的4～7阶IMF真实信号分量做重构，得到上游观测信号s1(t)，即：s1(t)=IMF4+…+IMF7。同理，可得到下游观测信号s2(t)。

3.2.4 Fast ICA算法的信号盲源分离

盲源分离是指在信号与其他无关信号相互混合，且混合方式未知的情况下，将信号从混合的复杂信号中独立地分离出来的处理方法。独立分量分析(Fast ICA)，又称为快速独立成分分析算法，是迭代速度最快、效率最高的一种盲源分离算法，利用Fast ICA算法提取泄漏信号的特征，可实现快速收敛，无需考虑不必要的参数。

利用Fast ICA算法对经CEEMD处理后得到的观测信号进行时域分析，从而可得到盲源分离后的上、下游泄漏信号，见图8和图9。

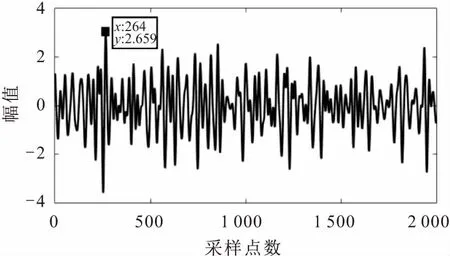
图8 经Fast ICA算法盲源分离后上游泄漏信号的 计算结果图Fig.8 Calculation result map of upstream leakage signals after Fast ICA algorithm blind source separation

图9 经Fast ICA算法盲源分离后下游泄漏信号的 计算结果图Fig.9 Calculation result graph of downstream leakage signals after Fast ICA algorithm blind source separation

3.2.5 时差计算及泄漏定位

通过计算上、下游泄漏信号采样点的差值，即可求得泄漏信号传播到两个传感器的时差Δt。由图8和图9中的泄漏信号采样点可计算表2中序号为1数据两点混合信号中的其中一个独立泄漏源的信号定位时差Δt，有Δt=(957-264)÷105=0.006 93 s。

已知管道泄漏点的位置x由泄漏信号传播到两个传感器的时差Δt和管道泄漏声波速度v所决定，因此只要求得Δt和v即可对管道泄漏点进行定位。管道泄漏声波速度不仅受管道材料的影响，还受到不同介质、工况的影响，且使用不同方法检测到的管道泄漏声波速度都有所差别。目前，国内外尚未形成统一的管道泄漏声波速度计算方法，不同研究人员检测计算得到的管道泄漏声波速度值也不一致。根据文献[18]，压缩空气介质所产生的声发射波在钢制管道中的传播波速为850～1 050 m/s，并通过大量试验对典型管道泄漏声波信号速度进行了测量，其中对65 m长的φ159×60 mm钢制管道的测量恰好与本文工况一致，因此最终确定管道泄漏声波速度平均值为950 m/s。于是，根据时差定位公式计算得到定位结果，即管道泄漏点的位置x=(40-0.006 93×950)÷2=16.71 m。

3.2.6 未剔除冗余分量的定位计算对比

杨凯[6]采用CEEMD方法对含噪地震信号进行了分解处理，但在其算法过程中并未对冗余分量做进一步处理。本文运用文献[6]的信号处理方法对表2中12个原始泄漏数据进行了定位计算处理，得到未剔除冗余分量的定位结果。将原始粗定位结果、未剔除冗余分量的定位结果与本文的精确定位结果进行了对比，三种定位结果的相对误差三维柱状图，见图10。

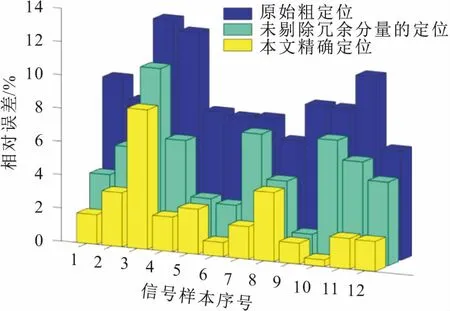
图10 三种处理方法定位的相对误差三维柱状图Fig.10 Three-dimensional histogram of the relative error of three processing methods

由图10可见，三种处理方法定位的相对误差有着明显的大小区分，具体来说，原始粗定位方法的相对误差较高，其平均相对误差为8.99%，未剔除冗余分量的定位方法的平均相对误差为6.36%，其定位精度与原始粗定位方法相比有了一定的提升；本文精确定位方法的平均相对误差为2.53%，与其他两种处理方法相比，其定位精度明显更高。

4 结 论

(1) 针对管道多点泄漏信号混杂、易受噪声干扰，而造成真实泄漏信号提取困难、定位不准等问题，本文提出了基于改进的CEEMD方法的管道多点泄漏定位分析方法。

(2) 通过对CEEMD分解方法进行改进，将各阶IMF分量显示为有效信号分量、噪声分量和冗余分量三种分量，可直接获取有效信号，从而提高了管道泄漏检测的效率，实现了管道泄漏检测的精确定位。

(3) 将本文精确定位方法与未剔除冗余分量的定位方法和原始粗定位方法进行了对比，结果表明本文精确定位方法和未剔除冗余分量的定位方法都能在一定程度上降低定位误差，但本文的定位方法能将相对误差控制在更小的范围内，同时适用于单点和多点泄漏，更符合泄漏管道的实际情况。

(4) 本文以圆孔为泄漏模拟点，未考虑泄漏孔不同形状、大小对管道泄漏定位的影响，这可作为进一步研究的方向。