核心素养下的问题情境教学与思考
——以《5.1位置的确定》为例
□胡连成
(丰县华山初级中学,江苏丰县 221700)
情境教育是基于我国传统文化和教育实践而提出的,具有中国特色的教育模式.情境教育首倡者李吉林老师提出“形真、情切、意远、理寓其中”和“以思为核心、以情为纽带、以美为境界”的教育理念[1].吕传汉和汪秉彝教授认为:数学情境教学就是以数学情景为基础,以数学问题为纽带的教学,其核心是学生问题意识的培养[2].笔者在教学实践中尝试开展了问题情境教学.下面以《5.1 位置的确定》教学设计为例,谈一谈自己的教学过程和思考.
一、问题情境的基础与前提
本课是苏科版教科书八年级上册第5 章第1节.学生已经了解数轴上的点与实数一一对应的关系,在此基础上对物体(点)位置确定进行探究与思考.本课既是本章的起始课,也是函数学习的起始课,通过生活中物体位置确定到平面上点的位置确定,从一维问题拓展到二维思考,并指向三维空间的位置探索,经历从实际问题到数学问题的数学化思考过程,通过抽象、推理与模型化的思维加工,可以较好地提升学生的数学核心素养.为学习“平面直角坐标系”及函数内容奠定基础.本课内容知识面广,方法思维线多,教学深度、广度不容易把握,平时教学往往一带而过,忽略挖掘教材中丰富的数学内涵.基于以上分析,确定了以下的教学目标和重难点.
教学目标:1.知道可以用数量(有序实数对)描述平面内物体(点)位置,并初步解决实际问题;2.了解位置变化可以引起数量变化、数量变化可以反映位置变化,感悟数形结合的数学思想,提高从运动变化的角度思考问题的意识;3.经历问题探究过程,培养学生主动参与、合作交流意识,提高发现、分析和解决问题的能力,增强数学应用意识.
教学重点:了解平面内物体(点)位置确定方法,运用不同方法描述其位置,理解有序实数对与位置变化的关系.
教学难点:灵活运用不同的方法确定物体(点)位置,体会数、形之联系.
二、问题情境设计的途径与方法
(一)创设情境 引发思考
“大道致远,海纳百川.”今年是习近平主席提出“一带一路”倡议6周年.
问题1:“21 世纪海上丝绸之路”途经南海、马六甲海峡、阿拉伯海、红海等海域.在茫茫大海上,如何确定轮船的准确位置?
【设计意图】在“一带一路”背景下,思考大海上位置确定问题,既体现问题的引领作用,又注重家国情怀的思想熏陶.在具有现实意义和数学内涵的问题情境中,产生“悱、愤”之惑,引领思考、讨论和争鸣.
(二)始于基础 方法初探
小明家所在的小区和学校位于同一条街道的两端,小明每天乘坐公交车上学.图1 是该公交线路的站点示意图.

图1
问题2:小明上学途中,如果把小区看作第一站,那么医院是第几站?第四站是哪里?
追问1:小明放学途中,如果把学校看作第一站,那么医院是第几站?
追问2:如果问第四站是哪里?你如何回答?要了解小明坐公交车时的具体位置,你还有什么方法吗?
【设计意图】学生已经学习了数轴的相关知识,知道数轴上的点与实数一一对应,在此基础上展开思考与探索.把公交线路上的位置确定抽象为直线上点的位置确定,经过问题串的变式思考,运用“由点求数”和“由数定点”的方法解决问题的过程,体会直线上的点与有序实数的对应关系.
(三)直观思考 方法探究
围棋,中国古代称为“弈”,是中华文明的象征之一,由纵横19条线将围棋分为361个格点,棋子走在格点上,双方交替行棋,以围地多者为胜.
问题3:在图2中,你如何表示棋盘中棋子A的位置?
追问1:在图3中,请你按照“先纵后横”的顺序描述棋子位置?
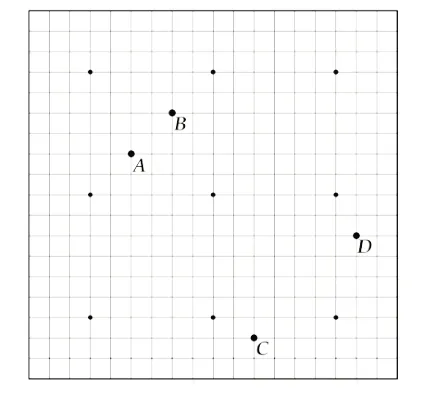
图2

图3
追问2:如果把“先纵后横”的顺序改为“先横后纵”,请说出棋盘上棋子的位置.
追问3:为什么棋盘中同一个点的位置有不同的表示方法?
追问4:如果棋子A沿着纵线运动到不同格点处,它的位置描述有怎样的变化?如果沿着横线运动呢?
追问5:请举出日常生活中,用类似方法表示位置的例子.
【设计意图】利用“围棋”设置情境,在探索棋子位置确定的同时,注重传统文化的熏陶.由图2 中棋子A的位置表达引起发散式思考,初探平面内物体位置的确定方法.再通过图3的相关追问,由“先纵后横”与“先横后纵”的方法比较,理解用“两个有序实数”描述位置的合理性.在追问4中,通过“点动数变”的思考,培养学生从运动变化角度思考问题的意识.在追问5 中,回顾日常生活中物体位置确定的实例,感受数学的应用价值,培养学生的数学应用意识.
(四)数学抽象 方法始成
问题4:如图4,点P在线段AB的垂直平分线m上,AB=2cm,连接PA,PB.当点P自上而下运动时,哪些量在变化?哪些量保持不变?
追问1:如何描述点P的位置?
追问2:点P运动到什么位置时,△PAB是等边三角形?
追问3:点P运动到什么位置时,△PAB是直角三角形?
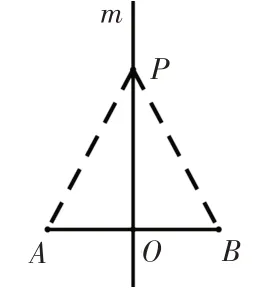
图4
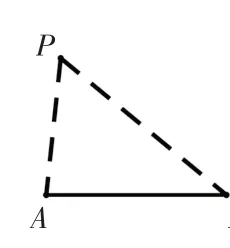
图5

图6
【设计意图】从运动角度设置情境,由点的运动引起数量的变化,由数量的变化思考对点的位置描述.教学中先通过想象点的运动过程,感知量的变化,再借助几何画板演示,体会“点动数变”的对应关系,培养学生几何直观和空间想象能力.进而思考如何利用变化的量描述动点P的位置,探索“距离+距离”“距离+方位角”“方位角+方位角”等方法,归纳其共性:用两个有序实数表示点的位置.通过追问2、追问3 的特殊化思考,化动为静,体会特殊与一般的联系.
问题5:如图5,平面内有动点P和线段AB,连接PA,PB,当点P运动时,哪些量会发生变化?
追问1:如何描述动点P的位置?你有哪些方法?
问题6:如图6,平面内有一动点P和定点A,如何描述点P的位置,你有哪些方法?
追问1:平面内有一动点P,如何描述点P的位置?
问题7:如果在一个立体空间内有一个动点P,你如何描述它的位置?
【设计意图】通过对条件的逐次弱化,体现从特殊到一般的数学思想.经过一般化的数学思考,归纳平面内位置确定方法的共性.并通过问题7引发对空间位置确定的思考.通过这种数学化的思维加工过程,培养学生问题意识,发展理性思维.数学教育家马明先生曾说:数学教学的本质是展示和发展思维的过程.从问题4 到问题7,利用“动点的位置确定”的系列情境,思考一般化解决策略,既注重思维灵活性的培养,又关注数学思想方法的领悟.在问题思考中体会特殊与一般的联系,在方法归纳中感悟数学抽象与模型思想.
(五)方法运用 解决问题
问题8:通过本节课的学习,你认为在茫茫大海上,如何确定轮船的位置?
【设计意图】“再回首”,通过思考大海上轮船的位置确定问题,实现对本课所学知识、方法的反思与构建;“齐展望”,为学习“平面直角坐标系”创设思考情境,以期继续思考与讨论.通过由外而内、由内而外的问题探索与思考,体现“生活数学”“问题思考”的教育理念.
三、问题情境教学的思考
(一)情境设计之“真、趣、美”
需要思考的问题情境必然是真实的、客观存在的.数学源于生活,可以从生活实际引入问题情境,思考数学内涵,增强数学应用意识;可以从数学史话引入问题情境,通过与数学家的心灵对话,了解数学发展历程,学习求真的探索精神;可以从数学活动中引入问题情境,在活动中思考数学奥秘,在思考中探索未知世界.
能吸引学生思考的问题必然是“有趣”的.有趣的问题情境是富于变化的问题形式、动态的图形运动,必能吸引住学生的眼球,引发主动思考;有趣的问题情境是赋予想象的情境,富有内涵的人文底蕴、广阔深邃的客观世界,引人入胜、趣在其中;有趣的问题情境是需要思考的情境,经过探索、思考、交流、合作,在苦苦寻觅中收获成功的喜悦.比知识重要的是方法,比方法重要的是兴趣,乐学之方能好学之.
值得思考的问题情境必然是充满“美感”的.问题情境的“美”,在于问题的数学美,在想象的引导下,归纳先行、演绎跟进,通过对客观世界的思维加工,探究简洁的数学规律、解决复杂的现实问题.从感性层面走向理性境界,实现知识整合、方法贯通、思想融汇,这正是数学妙不可言的“美”的体现.问题情境的“美”,在于问题的意境美,通过问题情境的谋势,情境交融,营造一种充满理性色彩的意境之美.以思为核心,以情为纽带,以美为境界.
本课中,从“一带一路”的家国情怀、“棋子对弈”的文化之韵,再到几何图形的运动变换,无不体现了“真、趣、美”的特点.马明先生认为:评价一节数学课是否成功,关键在于能否引发学生的思考.同样,情境设计是否得当,在于能否启发学生进行深度思维.正如本课,通过四个问题情境,由生活到数学、从直观到抽象,逐层深入、引人入胜.以情境问题作为知识探索的平台,以发展理性思维作为课堂教学的目标,只有这种蕴含数学本质的情境才能成为产生思维火花的土壤,我们的数学学习才能是一次智慧之旅.
(二)情境探索之“问题引领”
基于问题引领的情境探索要立足于学生的学情基础,结合“最近发展区”理论,通过有思维梯度的问题串引领,让学生蹦一蹦,够得着,这样才有利于学生持续的探索与思考.基于问题引领的情境探索要注重学生问题意识的培养,提出一个问题往往比解决一个问题更重要.基于问题引领的情境探索要利用问题变式实现问题驱动.郑毓信教授曾说“为讲方法而讲方法就不是讲方法的好方法[3]”,在教学中要给学生时间和舞台,在持续的问题探索中,通过想象、猜想、验证;经历分析、比较、归纳、抽象和推理,实现理性思维的发展.基于问题引领的情境探索要注重知识的内化和思维的外显.内化的途径是思考,通过思考实现知识建构、方法归纳和数学抽象、建模过程.外显的方式是交流展示,在解决问题中注重交流与合作、批判与反思,通过问题解决方法有条理地表达和展示,才能培养思维的缜密、逻辑的清晰.
正如本课的四次情境探索,从实际问题到数学问题的逐层深入,从生活现象到一般方法的抽象和建模,这都需要在问题引领下的思考交流中得以实现,让情境成为问题的源泉、让问题探索成为学习的载体、让思维发展成为探索的目的,我们的课堂才能充满理性情怀.
(三)情境教学之“理蕴其中”
基于问题引领的情境探索为培养学生的数学核心素养提供了舞台.在问题探索中,通过由外而内、由内而外数学化的思考过程,使学生学会思考、学会学习.在本课情境探索中,由棋子位置的思考到平面上点的位置的思考,通过方法比较,归纳平面上点的位置的确定方法,再运用归纳的方法来回答“大海上轮船位置确定问题”.在问题解决和思考中,培养学生用数学的眼光看问题,发展数学直观和数学抽象素养;用数学的思维想问题,发展逻辑推理素养;用数学的语言说问题,发展数学模型素养.
数学教学的主要目的是帮助学生学会思维,并能逐步养成理性精神.在本课情境探索中,利用问题变式实行问题驱动,通过方法比较、归纳思考、讨论交流,化“快想”为“慢思”,使静思与辨思相结合,内化与外显共作用,从而让思考更全面、更清晰、更深刻、更合理.在思维活动中,通过抽象、推理与模型等数学化过程,积累活动经验,实现知识、方法与思想的融合与构建,从而发展数学思维、培养理性精神.

