应用残差稠密网络的无监督单幅图像深度估计

马 利，曹一铭，牛 斌

(辽宁大学 信息学院，沈阳110036)

1 引 言

单幅图像的深度估计是计算机视觉中一个重要的问题.在语义分割、3D模型重构、自动驾驶等方面都有着极其重要的应用.在一般情况下，对于图像深度信息的估计都是通过使用图像内部的纹理、边缘等特征实现的.由于单幅二维图像中缺少三维几何信息，因此单幅图像的深度估计存在其自身的复杂性.近年来，随着深度学习的发展，神经网络被越来越多地应用于图像深度估计，并且取得了令人瞩目的成果.现有的多数方法需要利用高分辨率真实图像深度图信息对神经网络进行监督训练，而获取真实深度图信息通常是十分困难的.尽管已有支持深度信息测量的传感器应用于获取真实图像深度图信息，但是传感器本身存在自身的误差，并且测量精度易受到噪声的影响.因此，最近出现了很多基于无监督学习的单幅图像深度估计方法，这些方法直接让神经网络从图像或者视频中学习深度信息，而不再需要真实图像深度图信息进行监督.

Zhang等[1]提出应用残差稠密网络进行超分辨率重构，通过该网络能够从一系列低分辨率的图像中更好地提取局部信息，进而提高了高分辨率图像的重构质量.受其启示，为了更好地提取单幅图像的边缘等局部信息，从而提高深度信息估计的准确度，本文提出了一种应用残差稠密网络的单幅图像深度估计网络模型，该网络模型以编码器—解码器结构为基础，并引入与DispNet[2]类似的从编码器各模块到解码器各模块的跳跃连接(Skip connection)[3]，使前级的高分辨率信息可以得到充分利用；同时通过引入残差稠密网络模块，充分利用各网络层提取的特征信息，进而提取出更精细的图像局部特征，这使网络输出的深度图表现出更细致的物体轮廓信息.除此之外，该网络模型在训练的时候通过使用一系列立体图像对实现神经网络的无监督训练.在训练结束之后，将单幅图像输入到网络中，得到相应视差图，再根据视差图与深度图的几何关系便可以得到输入图像的深度估计.

2 相关工作

图像的深度估计对于从2D图像中理解3D信息起着至关重要的作用.早期的图像深度估计方法都是基于几何特征或者手工特征.例如，Saxena等[4]使用多尺度的马尔可夫随机场来提取图像的全局特征与局部特征，以此实现图像深度估计.Liu等[5]将图像建模为超像素，再通过离散-连续优化的方式得到深度图.但是，这种依靠几何与手工特征所得到的深度图，大多因为缺少细节信息而较为模糊，而细节信息对于计算机视觉的许多应用都是十分必要的.

近年来，神经网络被应用于图像的深度估计，并取得了十分优异的结果.越来越多的基于神经网络的深度估计方法被提出.Eigen等[6]最先提出应用多尺度卷积神经网络进行图像深度估计的方法，该方法使用不同尺度的网络分别提取图像的全局信息和局部信息，最后再将两者进行融合得到高分辨率的深度图.Liu等[7]将卷积神经网络与条件随机场融合以求取图像的深度图.Li等[8]使用双流网络分别提取深度信息和梯度信息最后将两者进行融合的方法来进行深度估计.Laina等[9]通过将残差网络引入到全卷积网络结构来实现图像的深度估计.与早期的方法相比，这些方法的结果有了明显改善.但是这些方法都需要图像的真实深度图来训练网络，由于真实深度图提取困难，从而增加了实现难度.

为了避免由于求取真实深度图困难对深度估计的限制，近年来学者们提出了基于无监督的深度估计方法.例如，Garg等[10]通过使用双目立体图像对实现无监督的图像深度估计.该方法通过用左视点图像生成视差图，再用视差图与右视点图像合成左视点图像的预测图像，通过最小化预测图像与真实图像之间的差距以实现网络的训练，最终根据视差图生成深度图.而Godard等[11]在此基础上进行改进，提出左右图像一致性的训练方式，同时引入了效果更好的损失函数，进一步改善了深度估计的结果.Zhou等[12]通过使用视频图像中相邻时间点的图像间的内部约束实现无监督的深度估计，而Zhan等[13]通过将与文献[11]相似的方法应用于视频图像来实现对于深度信息的提取.

受到Zhang等[1]提出的应用于超分辨率的网络模型的启发，并通过结合单幅图像深度估计的具体情况，本文提出了应用残差稠密模块的网络模型.受到文献[10，11，13]利用双目摄像机对于同一场景同时拍摄所得到的立体图像对来训练网络的思想所启发，本文使用一系列立体图像对来对残差稠密网络模型进行无监督训练，实现图像的深度估计.本文所提出的网络应用于KITTI驾驶数据集[14]，与现有的方法相比较，得到了更高的准确率和更小的误差值，而且本文所得到的深度图具有更细致的物体边缘信息.

3 应用残差稠密网络的网络模型结构

本文通过引入残差稠密模块，提出了一种新的应用于单幅图像深度估计的神经网络模型，并通过使用一系列的立体图像对来对网络进行无监督训练.本章将对该方法的各个部分进行详细介绍.

3.1 残差稠密单元RDU(Residual Dense Unit)

神经网络中，随着网络层数的增加，网络能够提取出的特征信息的级别也会变得越高，因此神经网络的层数是影响其效果的重要因素.但是随着网络层数的增加，网络同时会出现退化问题.为了解决神经网络的退化问题，He等[15]提出了残差网络基元，如图1(a)所示.该基元通过使用恒等映射，将模块的输入直接引入到输出的前级，以此解决了神经网络的退化问题，同时使得网络的参数更容易训练.Tong等[16]提出了一种应用于超分辨率的稠密网络基元，其基本结构如图1(b)所示.该基元通过将每一层的输入连接到其余各层的方式，充分利用了各网络层提取的特征信息，但是这种方法存在训练困难的缺点.

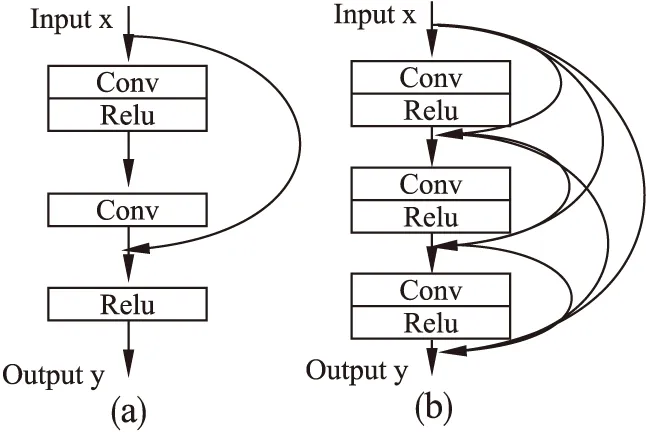
图1 残差网络基元和稠密网络基元Fig.1 Residual network block and dense network block

本文所使用的残差稠密基元RDB(Residual Dense Block)是将残差网络基元与稠密网络基元相融合，在稠密网络基元的基础上添加残差网络基元的恒等映射,再经过一些改进而得到的，其具体结构如图2所示.

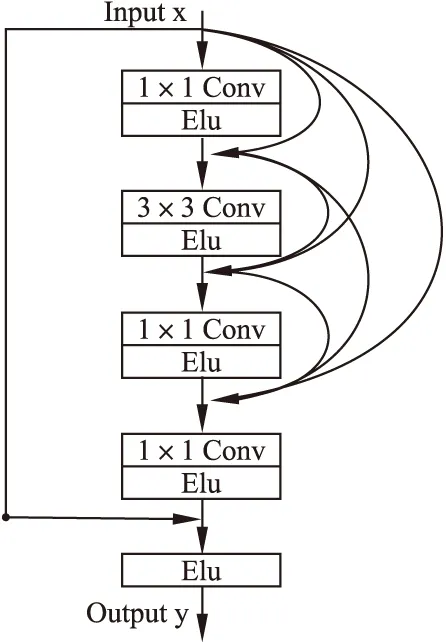
图2 残差稠密基元Fig.2 Residual dense block

本文使用的残差稠密基元分为四个卷积层，其中第一层使用1×1的卷积核，第二层为3×3的卷积核，第三层为1×1的卷积核，第四层为1×1的卷积核，前三层的stride为1，第四层的stride通过输入设置.四层之间使用稠密网络进行连接.同时，各个卷积层选用Elu(exponential linear units)[17]作为激活函数，并在输出之前，引入残差基元的恒等映射，将前四级的输出与基元输入进行融合，之后再经过Elu函数，得到最终的输出.这里，通过融合残差网络基元与稠密网络基元得到的残差稠密基元，不仅可以避免神经网络的退化问题，而且还使各层网络提取的特征得到了充分的利用，这使该网络模块表现出更好的局部特征提取特性，同时还解决了稠密网络难以训练的问题.

将若干个残差稠密基元首尾相接，便可以得到本文所使用的残差稠密单元RDU(Residual Dense Unit)，如图3所示.其中的每一个RDB都与上文提到的结构相同，但是前n-1个RDB的stride为1，第n个RDB的stride为2.

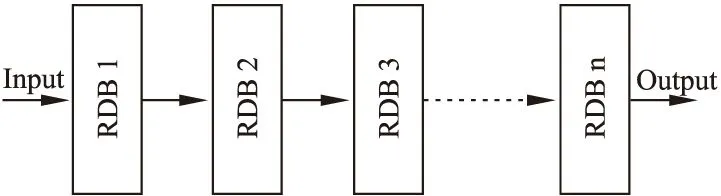
图3 残差稠密单元RDU的结构Fig.3 Structure of residual dense unit

通过多级残差稠密基元的融合，网络模型可以提取出图像中更高级别的信息，使各级模块提取出的信息得到更充分地利用，并提取出更细致的图像局部特征.

3.2 基于立体图像对的无监督训练的实现

相较于监督学习，无监督学习不需要经过标定的训练数据集，在深度估计问题中，这意味着不需要真实深度信息，极大地降低了对于数据集的要求.本文所使用的无监督训练方法，只需要由双目摄像机提供的一系列立体图像对，以及摄像机的基准距离和焦距便可以实现对于神经网络的训练.本文对于神经网络的训练方式与文献[11]类似，其主要思想为：

Dp=b·f/disp

(1)

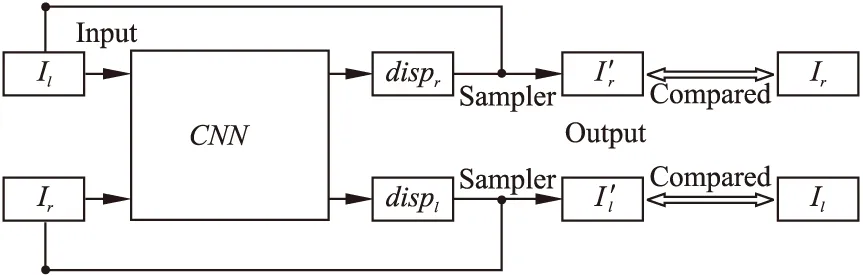
图4 无监督训练基本思想Fig.4 Idea of unsupervised

其中，Dp为神经网络输入图像的深度估计；b为左右两个摄像头之间的基准距离；f为摄像头的焦距；disp为相应视差图.

3.3 网络结构

本文使用编码器解码器(encoder-decoder)结构，并在普通的编码器解码器结构之上，添加了从编码器模块到对应解码器模块的跳跃连接，使解码器可以获得更高分辨率的图像信息.具体网络结构如图5所示.

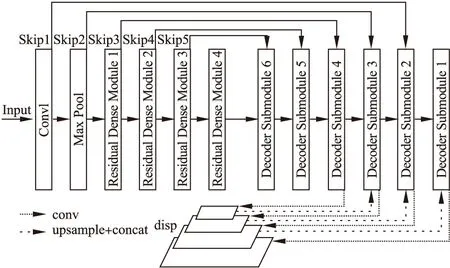
图5 网络结构Fig.5 Network structure

本文的神经网络可以分为三部分：

1)编码器部分：这部分又分为两个子部分：全局特征提取模块(Conv1+Max Pool)和局部特征提取模块(Residual Dense Module 1-4).全局特征提取模块由一个7×7的卷积层和一个最大池化层组成，局部特征提取模块由四个RDM(Residual Dense Module)组成，其中RDM是由n个RDU首尾相接所组成的模块.编码器首先使用全局特征提取模块对整幅图像信息进行全局提取，再通过局部特征提取模块对图像的细节信息进一步提取，以获得更全面的图像信息.

2)解码器部分：这部分由6个解码器子模块DSM(Decoder Submodule)构成，每个子模块都包含一个上卷积层和一个卷积层，其中上卷积层的输入为上一层的输出，卷积层的输入为相应上卷积层的输出与跳跃连接的合成.同时DSM4—DSM1会分别经过上采样输出视差图disp4-disp1.解码器部分通过各个解码器模块将高层信息降维，同时恢复图像信息的分辨率，最终获得disp4—disp1四个不同分辨率的视差图.

3)跳跃连接部分：分别从编码器的各层输出直接跳跃连接到解码器的各对应卷积层，具体的连接方式可参见图5.该部分通过跳跃连接，直接将编码器各模块所得到的信息引入到解码器各个模块，使解码器模块可以得到更高分辨率的图像信息，同时还可以使前级编码器信息得到充分利用.

该网络最终输出了由不同分辨率的视差图disp1-4构成的视差金字塔，其中视差图disp1-4都用于损失的计算，使用的损失函数在3.4节中详细介绍.而在训练结束之后，使用disp1生成输入图像的深度图.本文网络模型的具体参数如表1所示.其中conv和iconv为普通卷积操作；Pool为最大池化；RDM代表残差稠密模块，其具体结构如图2、图3所示；RDU×n表示连续的n个RDU首尾相连；DSM代表解码器子模块(Decoder Submodule)；upconv为上卷积操作；upsample为上采样操作.

3.4 损失函数

本文方法所使用的损失函数Ltotal为disp1到disp4的总和，即：

Ltotal=Ldisp1+Ldisp2+Ldisp3+Ldisp4

(2)

而每一个Ldisp由三部分组成：

Ldisp=w1Lm+w2Ls+w3Lc

(3)

其中，Lm是匹配损失，Ls是平滑损失，Lc是一致性损失，w1，w2，w3分别为三者的权重，其具体的设置在4.1中说明.因为本文的网络模型输出左右双视点图像的预测图像，之后再与原视点图像进行比较，所以会存在左右双视点的损失，也就是说，三种损失都由左视点损失与右视点损失两部分构成，即：

(4)

下面分别给出三种损失的计算公式：

(5)

(6)

其中，N为像素总数，α为权重系数.SSIM反映图像的结构相似性，L1反映图像的差异性，本文方法中对于结构相似性的要求更高，因此将SSIM项的权值设置的较大.经过试验，在α为0.85时得到了较好的效果，因此本文最终将α设置为此值.

11月23日，国务院印发了《关于支持自由贸易试验区深化改革创新若干措施的通知》（以下简称《若干措施》）。《若干措施》围绕自贸试验区建设发展需要，在营造优良投资环境、提升贸易便利化水平、推动金融创新服务实体经济、推进人力资源领域先行先试等方面，加大改革授权，加大开放力度，给予政策扶持，体现特色定位，提出了53项切口小、见效快的工作措施，着力打通有关工作的堵点、难点，推动自贸试验区更好发挥示范引领作用。

平滑损失：该损失用于平滑视差图displ,r的梯度，以减少深度图的不连续.具体计算方法如公式(7)、公式(8)所示.

表1 网络模型具体参数
Table 1 Network model parameters

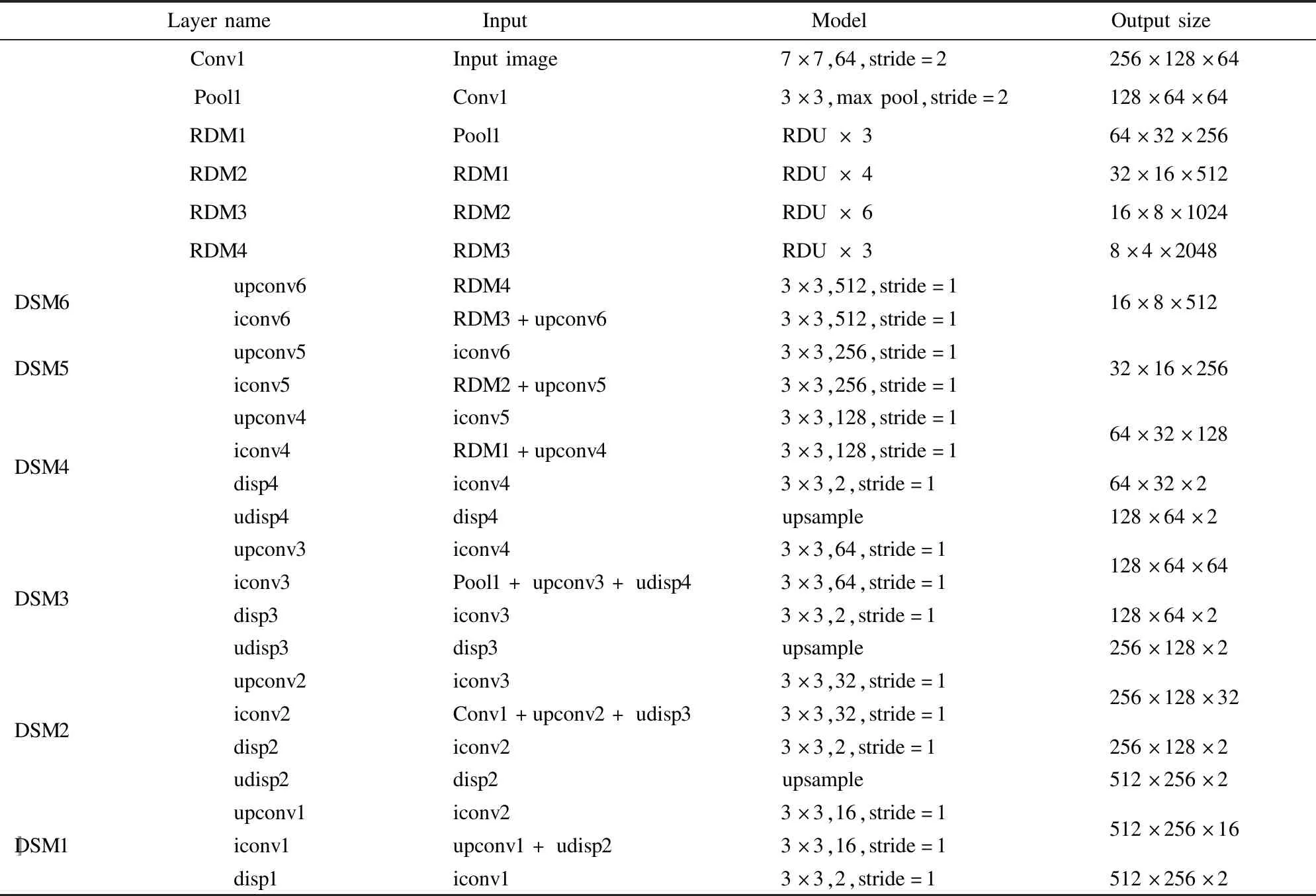
LayernameInputModelOutputsizeConv1Inputimage7×7,64,stride=2256×128×64Pool1Conv13×3,maxpool,stride=2128×64×64RDM1Pool1RDU×364×32×256RDM2RDM1RDU×432×16×512RDM3RDM2RDU×616×8×1024RDM4RDM3RDU×38×4×2048DSM6upconv6RDM43×3,512,stride=1iconv6RDM3+upconv63×3,512,stride=116×8×512DSM5upconv5iconv63×3,256,stride=1iconv5RDM2+upconv53×3,256,stride=132×16×256DSM4upconv4iconv53×3,128,stride=1iconv4RDM1+upconv43×3,128,stride=1disp4iconv43×3,2,stride=1udisp4disp4upsample64×32×12864×32×2128×64×2DSM3upconv3iconv43×3,64,stride=1iconv3Pool1+upconv3+udisp43×3,64,stride=1disp3iconv33×3,2,stride=1udisp3disp3upsample128×64×64128×64×2256×128×2DSM2upconv2iconv33×3,32,stride=1iconv2Conv1+upconv2+udisp33×3,32,stride=1disp2iconv23×3,2,stride=1udisp2disp2upsample256×128×32256×128×2512×256×2DSM1upconv1iconv23×3,16,stride=1iconv1upconv1+udisp23×3,16,stride=1disp1iconv13×3,2,stride=1512×256×16512×256×2〛

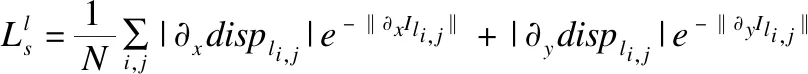
(7)

(8)

一致性损失：该损失用于描述网络输出的左右两幅视差图之间的一致性，目的是减小左视差图与右视差图的对应像素之间的差距.其计算方法如公式(9)、公式(10)所示.

(9)

(10)

总的来说，本文通过对基于残差稠密模块的编解码器网络模型进行训练，得到输入图像的视差金字塔，再通过使用公式(1)计算出对应的深度图，即本文最终要得到的对于输入单幅图像的深度估计.需要说明的是，本文的方法只有在训练的时候，才需要使用左右双视点图像，而在训练结束后，只需要输入单幅图像即可得到最终的深度估计.

4 实验与结果分析

该部分将对本文的实验进行详细地说明，并在KITTI数据集上与几种具有代表性的图像深度估计方法进行比较，其中既包含Eigen等[6]、Liu等[7]的监督学习方法，又包含了Godard等[11]和Zhan等[13]的无监督学习方法，分别在误差和准确率以及视觉深度效果上验证了本文方法的可行性.

4.1 具体实现

本文的实验平台为：至强4核E3处理器、4片NVIDIA GTX 1080 显卡、32G显存的主机.神经网络使用Tensorflow实现，包含9267万参数，训练时间约为46小时，输入图像的大小为512×256.

表2 在Eigen Split集上的结果
Table 2 Results on the Eigen Split set

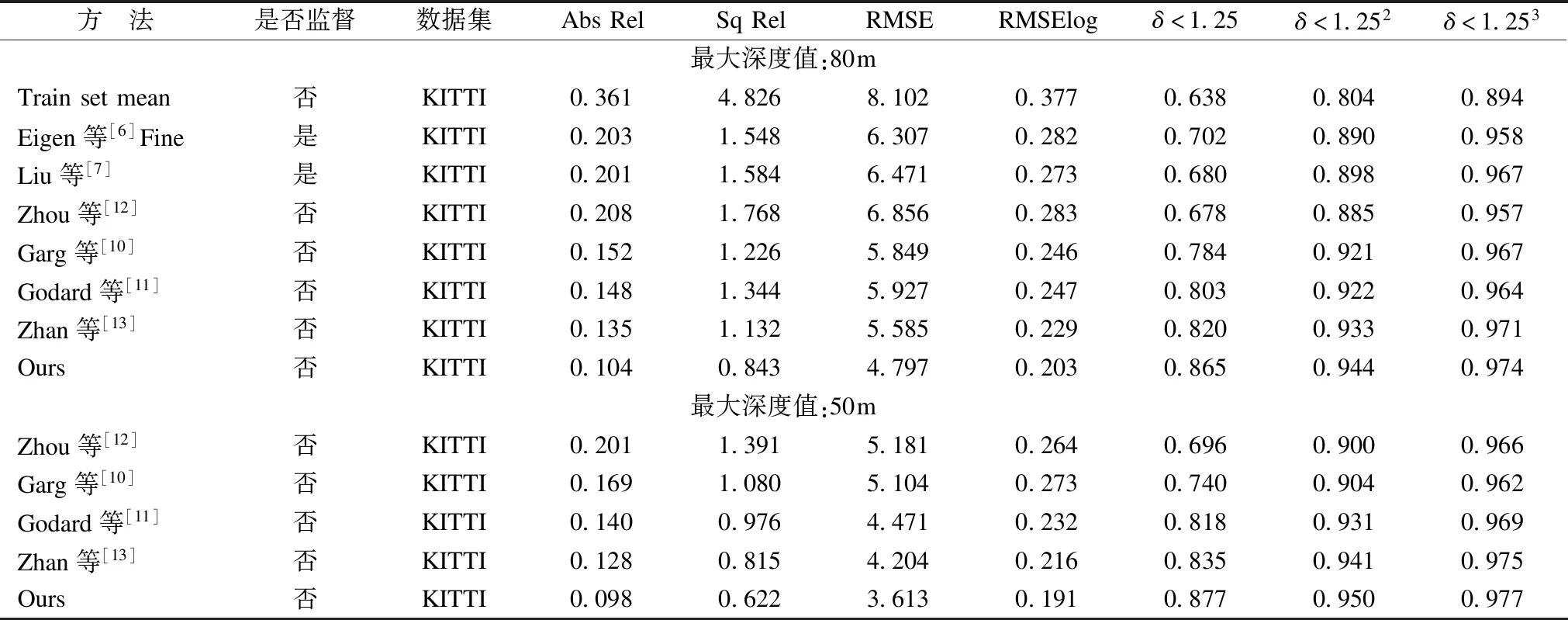
方 法是否监督数据集AbsRelSqRelRMSERMSElogδ<1.25δ<1.252δ<1.253最大深度值:80mTrainsetmean否KITTI0.3614.8268.1020.3770.6380.8040.894Eigen等[6]Fine是KITTI0.2031.5486.3070.2820.7020.8900.958Liu等[7]是KITTI0.2011.5846.4710.2730.6800.8980.967Zhou等[12]否KITTI0.2081.7686.8560.2830.6780.8850.957Garg等[10]否KITTI0.1521.2265.8490.2460.7840.9210.967Godard等[11]否KITTI0.1481.3445.9270.2470.8030.9220.964Zhan等[13]否KITTI0.1351.1325.5850.2290.8200.9330.971Ours否KITTI0.1040.8434.7970.2030.8650.9440.974最大深度值:50mZhou等[12]否KITTI0.2011.3915.1810.2640.6960.9000.966Garg等[10]否KITTI0.1691.0805.1040.2730.7400.9040.962Godard等[11]否KITTI0.1400.9764.4710.2320.8180.9310.969Zhan等[13]否KITTI0.1280.8154.2040.2160.8350.9410.975Ours否KITTI0.0980.6223.6130.1910.8770.9500.977

4.2 训练集与测试集

本文实验的训练和测试都基于广泛使用的KITTI数据集.该数据集包含从61个场景中得到的42382对经过修正的图像，其原始的图像分辨率为1242×375.本文所使用的分辨率为512×256的图像由原始图像处理得到.

Eigen Split：该数据集由Eigen等[6]提出.Eigen等从原始KITTI数据集的29个场景中选择697幅图像作为测试集.在余下的32个场景中的23488幅图像中，选取22600幅图像用于训练，其余的图像用于评估.为了能够与使用该数据集的大部分方法进行比较，本文在该数据集上的测试使用文献[6]提出的裁剪方法，同时使用输入图像的分辨率进行评估.评估的指标使用广泛应用的平均相对误差Abs Rel、平方根相对误差Sq Rel、线性均方根误差RMSE、对数均方根误差RMSElog及准确率δ.其具体计算公式参见文献[6].

在评估时，平均相对误差Abs Rel、平方根相对误差Sq Rel、线性均方根误差RMSE、对数均方根误差RMSElog的值越小表示结果越好，准确率δ的值越大表示结果越好.本文与几种有代表性的方法的实验数据评估结果如表2所示，其中所有方法的训练集都是KITTI数据集，Eigen等[6]和Liu等[7]是有监督的方法其余方法都是无监督的.为了验证不同景深情况下的算法性能，表中上半部分是各个方法在最大深度值设置为80米时所得到的数据，下半部分是最大深度值设置为50米时所得到的数据.对于在Eigen Split中比较有代表性的几幅图像的深度估计结果如图6所示.

4.3 结果分析

从表2可以看出，在与几种代表性方法的比较中，本文的方法在不同景深情况下，无论是在误差方面还是在准确率方面都得到了较好的结果.在图6中可以发现，尽管Eigen等[6]和Liu等[7]是基于监督学习的方法，但是他们的实验结果只是给出了输入图像的大致深度图，图像中物体的深度估计是十分模糊的，而本文方法所得到的结果更为细致.与同为基于无监督训练的Godard等[11]以及Zhan等[13]的结果相比较，尽管三种方法在所选取的几幅图像上对于各个物体的识别情况大致相同，但是本文所提出的方法给出了更为细致的物体边缘信息.例如在图6中，第一幅图像中右下角的护栏、中间的树木等，本文的实验结果给出了比Godard等[11]以及Zhan等[13]的结果更为清晰的边缘信息；第二幅测试图像中对于位于中间的人的头部、左侧复杂背景的信号灯等部分，本文的实验结果都给出了更为清晰的轮廓，而在Godard等[11]和Zhan等[13]的结果中，几乎没有体现；第三幅图像中对于右下角的电动车以及靠左上方的树干及树叶边缘，本文也都给出了更为清晰的轮廓.

与Eigen等[6]以及Liu等[7]的方法相比较，本文的方法采用了更深层次的网络，可以提取出更高层次的图像信息，后级网络，不仅使前级信息得到更充分的利用而且使后级网络得到了更高分辨率的图像信息.最终使本文的网络既能更好地识别图像中的物体信息又能显示出更高的分辨率.

图6 在Eigen Split上的实验结果对比Fig.6 Comparison of experimental results on Eigen Split

与Godard等[11]以及Zhan等[13]的方法相比较，尽管三种方法都采用了相似的无监督训练方式，但是本文引入的残差稠密模块，通过模块内部的多级信息的充分利用，更好地提取出图像的局部特征信息，使本文的方法在深度估计中可以得到更细致的物体轮廓信息.

综上所述，本文所提出的方法在误差和准确率方面表现出了较好的数据结果，而且可以得到更为细致的物体轮廓信息，提高了单幅图像深度估计的质量.

5 总 结

本文提出了一种基于神经网络的单幅图像深度估计方法.该方法以编码器解码器网络模型为基础，并在编码器部分引入连续的残差稠密模块，在解码器部分引入来自编码器模块中的跳跃连接的方式改进网络模型.经过这种改进，本文所提出的神经网络模型可以充分利用各级网络所提取出的特征信息，使得网络表现出了更为细致的局部信息提取特性.与此同时，本文通过使用一系列立体图像对来训练神经网络的方式，摆脱了对于真实图像深度需求的限制，实现了网络模型的无监督学习.通过在KITTI驾驶数据集上的验证，本文所提出的方法相较于几种有代表性的方法，在误差和准确率方面都得到了更为优异的结果，在视觉上可以给出具有清晰物体边缘的深度估计.但是，本文所提出的网络增加了一定量的参数，这导致网络的训练时间有所增加.笔者未来将对该网络的基本结构以及训练方式上做进一步的研究.