首错误特征分析在程序故障行为分类中的应用
朱丽娜,蒋曹清,夏国恩,张作昌
1(广西财经学院 信息与统计学院,南宁 530003)2(广西财经学院 广西跨境电商智能信息处理重点实验室,南宁 530003)
1 引 言
与硬件相比,软件的可靠性评测有许多特殊之处.例如,软件寿命与其失效率无关,在其他各项指标保持不变的情况下,软件可以持续正常运行,不存在硬件系统的种种损耗机理;另外,由于软件的不可触摸性,判断软件产品的可靠性时,无法从其尺寸、质量、技术规范等直观衡量尺度着手,只有当软件运行之后才能对其可靠性进行评测.失效数据的收集是评测软件可靠性的关键前提,同时也是其瓶颈之一.这是由于软件在系统测试或投入运行之后,其操作周期往往较长,且此时故障引发失效的概率较低,导致收集到的失效数据极其有限,直接影响可靠性预测模型的建立.此外,迫于竞争压力,很多企业选择保护其实验或测试阶段收集的失效数据,使得该领域缺乏充足的公开数据集.这些都直接阻碍了软件可靠性的研究工作.
尽管软、硬件存在诸多差异,但也有相似之处.例如,软、硬件的可靠性均为复杂度的函数,后者是设备复杂度的函数,前者是代码量、算法复杂度的函数.对于硬件设备来说,造成失效的缺陷是在制造环节引入的,若在制造期间严格保证质量,设备可在较长时间的使用过程中发现零耗损机理,软件亦然.严格控制编码阶段引入的错误量可以保证较高的软件可靠性.类比元器件的失效机理,是否可对软件失效机理做类似区分?这既是本文的研究动机,也是核心内容.
本文将探讨软件是否存在某种特定的失效机理,使得它可以区别于其他软件,并呈现出某种特定的可靠性特征?对这一抽象问题的研究可归结为:是否有一种针对软件的分类方法,可以将具有同种特质的软件划归为一类,使得类内的软件具有相似的可靠性属性?本文的研究工作建立在文献[1]的基础上,对程序的状态特征描述采用基于细粒度基本块(Fine Granularity Basic Block,FGBB)的程序状态提取方法,依据程序“首错误”特征进行状态划分.
2 相关工作
失效机理原指机械工程领域引发失效的物理、化学或其他的原因和过程,主要特点包括:失效机理是失效模式的原因;失效机理的类别有限,且相对容易被识别;通过对失效机理分析而积累的工程知识可用于同领域的其他产品.类似的,分析软件的失效机理可从以下方面着手:
1)程序的结构特征;
2)故障在软件系统中的传播特征;
3)软件失效的回溯过程,即失效与故障的映射关系.
现从这三个方面梳理相关研究进展.
失效机理的研究初衷是为了探讨软件与其可靠性之间的关系,而失效数据是可靠性研究的重要前提.对程序结构特征的研究主要是指基于白盒测试、故障分类、故障诊断等程序结构建模与分析.文献[2]提出一种基于可靠性的故障关联静态分析优化方法,用以对大型嵌入式系统进行故障检测.文献[3-5]通过白盒、灰盒测试,分析测试用例的覆盖率,对软件错误做出定性分析.
故障传播作为一个独立的领域,包括故障定位和检测、可靠性预测等,是软件失效机理的研究热点之一.多数文献将故障传播的研究视为自身研究领域的延展,故障传播的各类建模方法之间并不通用.目前,该领域主要有两大研究趋势,一是假定软件的结构特征决定故障传播行为,重点研究故障在软件自身的体系结构内的传播规律[6-8];二是假定故障行为特征(而非程序固有的结构特征)本身决定其传播规律,从而将研究着眼于故障特性上[9,10].
从软件失效到故障或错误的回溯分析,较为出众的研究成果常以程序谱系作为研究起点.谱系是一种描述程序行为特征的有效方法,首次在文献[11]中提出.目前,程序频谱主要以程序的语句、分支、函数或谓词等作为程序实体类型,用以建模分析程序行为.在网络安全(Masri提出了Tarantula方法,针对信息流的程序实体间关系建模)[12]、故障定位与检测(Chen等人提出了包含程序频谱构造、测试套件构成和维护、内在缺陷数量、测试用例预言设置等方面的故障定位研究框架)[13]等领域均有不错的研究成果.而试图通过聚类的方法判断和寻找程序的失效机理的研究,近年来,以文献[14]为典型.Zhang等人通过建立程序行为在多种条件下的特征谱(正常行为、故障行为和失效行为等)并对其聚类分析,用以探讨软件故障、错误或失效行为与正常行为之间的关系,结果表明,在特定的系统平台下,程序确实具有某种固有属性可用于分类程序的行为特征.
本文研究与文献[14]有相近之处,即试图通过建立程序行为并划分类别来探讨软件失效机理的问题.不同之处在于,本文在文献[1]的基础上,建立与首错误特征相关的程序行为谱,并基于故障的时空间分布特性对故障、错误和失效行为进行特征提取,更符合软件可靠性的核心研究思路.主要内容包括:定义三种与程序行为特征相关的特征谱系表达,即黄金运行、错误行为和失效行为;根据谱系表达的特点提出各个表达之间相似性的度量方法和分类方法,阐述对分类准确性的评定方法;以SPEC 2006基准程序为研究对象,将服从真实场景时空间分布的正交缺陷分类(Orthogonal Defect Classification,ODC)故障注入程序中,获取真实的现场失效数据;分析三种分类方式下的程序行为特征,对其呈现的软件失效机理的效果做出详细分析和评定,探讨研究软件失效机理的合理性及意义.
3 三种程序特征表达的定义方法
3.1 基于FGBB的程序黄金运行特征表达
程序运行过程可总结为:在特定的操作剖面下,程序经过一组指令序列执行后得到输出值的过程.“可重复性”是程序的本质,即在无故障条件下,相同的操作剖面一定会产生相同的程序输出.本文采用“黄金运行”来定义这种“可重复性”,试图以此为切入点来探讨软件的失效机理问题.此处,在文献[1]提出的FGBB方法的基础上,进一步定义和探讨程序的黄金运行及其特征表达.
FGBB方法的主要思想是,在错误发生时能做出及时的性质判定和位置判定,尽可能在故障引发的首个程序异常状态处做出响应.FGBB方法将程序的运行状态分为5类:
状态类型1:指无条件跳转指令之后对应的程序状态(包含跳转条件和当前栈帧信息),记做UJS.根据其指令特性,在记录中间状态时,将表示控制流特性的标志位始终置1,表示如下:
UJS={stat1,jmpCond,%ebp,stackSize,stackContent},jmpCond=1
状态类型2:指条件跳转指令之后对应的程序状态(包括跳转条件和当前栈帧信息),其中,跳转条件是根据寄存器EFLAGS中条件码的特定组合得到的布尔表达式的值,记做CJS,表示如下:
CJS={stat2,jmpCond,%ebp,stackSize,stackContent}
状态类型3:call指令执行之后获取的与栈帧结构相关的程序状态,记做CLS,表示如下:
CLS={stat3,%ebp,stackSize,stackContent}
状态类型4:在被调函数返回前,且从被调函数栈帧切换至调用函数栈帧前,执行的最后一条指令后的程序状态,记做BRETS,表示如下:
BRETS={stat4,%eax,stackSize,stackContent},or
BRETS={star4,stackSize,stackContent}
状态类型5:ret指令执行后获得的与当前栈帧结构相关的程序状态,记做ARETS,表示如下:
ARETS={stat5,%ebp,stackSize,stackContent}
若考虑用上述状态集Ω={UJS,CJS,CLS,BRETS,ARETS}表征程序的一次运行过程,则可以用如下状态序列表示:{s1,s2,…,sn},其中si∈Ω,即所有的程序状态序列都可看作是由Ω集合中的5种状态构成的线性序列.采用长度为k的滑动窗口沿状态序列以步长为1的方式依次移动直至最末状态,则可将程序状态分解为由多个k-长状态子序列过程的状态集合.程序状态序列对应程序的结构特征,如CJS对应一次条件判断,一组
单次程序的状态序列并不能全面反映程序的行为特征,为得到统计意义上的程序行为特征,必须基于一簇输入值下的程序状态序列来分析,且该输入集合尽可能接近真实的用户操作剖面.
把获得的状态序列集合依次提取6-长子序列,若状态序列长度为L,则子序列个数为L-5.统计不同子序列出现的次数得到频率分布:{P(seq1),P(seq2),…,P(seqn)}.其中,seqi表示一个特定的6-长子序列,且n=56=15625.为保证实验结果的准确性,在实验获得的全部子序列频率分布中seqi的绝对位置不变.
每个程序在给定的操作剖面下均可获得一个关于子序列的频率分布,由于子序列能反映程序固有的结构特征,而结构特征通常由程序功能特征决定,因此,子序列的频率分布是具有统计意义的程序黄金运行.考虑程序无故障的运行情况,若实验环境下的操作剖面越接近用户的真实使用场景,该频率分布越能准确地反映程序的基本运行特征.
3.2 基于FGBB的程序故障行为特征表达
程序的故障行为特征表达包含错误行为特征和失效行为特征,分别在3.2.1节中3.2.2节中定义和阐述.
3.2.1 程序的错误行为特征
根据程序的可重复性,运行时的中间数据具有多次运行呈现的某种不变性约束的逻辑关系特征.基于文献[1],假定U(stari,stati+1)是程序在某输入条件下无故障时的一次状态转移过程,F为故障集,把程序在故障条件下的错误行为划分为如下4类:
错误类型1:程序状态类型在运行时出错,即由于故障的影响,产生了一个非正常的程序状态,记做:
错误类型2:当前栈帧结构中的返回地址出错,可能导致程序的控制流发生改变,并影响程序的后续运行,记做:
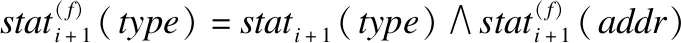
=stati+1(stack)
错误类型3:包括函数参数、局部变量和其他中间计算特征等中间数据出错.该错误通常有潜伏期,若程序具有良好的容错能力,错误可能会被屏蔽,记做:
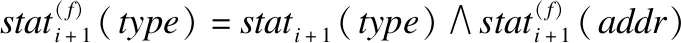
=stati+1(retval)
错误类型4:函数的返回值出错,可能影响包括变量赋值、函数参数值等在内的中间数据,记做:
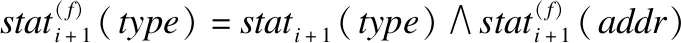
=stati+1(stack)
故障触发的类型和位置均与程序的代码片段特征有关,将代码片段的特点和故障的发生位置相关联,用如下序列表示故障在特定程序中的空间分布:
{P(f1),P(f2),…,P(fn)}
其中,fi表示故障类型,P(fi)表示故障发生概率.
假定程序中某一类错误发生的概率为P(ei)(ei∈{Errstat,Errretaddr,Errstack,Errretval},i=1,2,3,4),基于全概率公式,程序在故障条件下触发某类错误的概率为:
另外,考虑具有较长潜伏期的故障,程序的状态序列可能与黄金运行相同,程序的错误行为特征可抽象为频率分布{P(e0),P(e1),P(e2),P(e3),P(e4)},其中e0表示程序未发生任何错误,状态序列与黄金运行一致.为保证结果的一致性,ei在各频率分布中的绝对位置不变.
3.2.2 程序的失效行为特征
程序的失效行为分为异常终止、响应超时和非法输出.与3.2.1节类似,定义程序的失效行为时考虑故障的空间分布特征:假定程序的某一失效类型为failj,基于全概率公式,程序在故障条件下引发失效failj的概率计算如下:
考虑程序在故障条件下输出正常的情况,程序的失效行为特征可定义为{P(fail0),P(fail1),P(fail2),P(fail3)},其中,fail0为正常输出的行为,后三者分别对应异常终止、响应超时和非法输出,failj在频率分布中的绝对位置不变.
4 程序特征表达间的相似性度量及分类方法
由上节可知,程序的黄金运行、错误行为和失效行为表达均被定义为频率分布.6-长子序列、错误和失效为随机变量,其行为的特征表达即为概率分布.采用Kullback熵(即KL散度)[15]度量各个特征表达之间的相似性,根据相似性对程序集进行分类,得到三组不同的分类结果,分别为黄金运行、错误行为和失效行为.上述过程总结如下:
1)对每个程序的三组特征表达分别做Kullback熵度量,得到两两程序之间关于每组特征表达的相似性度量值;
2)根据相似性度量得到程序的相似矩阵,一共生成三个相似矩阵;
3)将相似矩阵变换为二维空间中的点集,使得每个程序对应二维空间中的一个标识;
4)采用聚类方法将二维空间中的点集分成三类,即黄金运行分类、错误行为分类和失效行为分类.
4.1 程序特征表达的相似性度量方法
程序行为的谱系表达均为概率分布,采用Kullback熵衡量两个程序行为之间的距离,以表征两两行为之间的相似性.假设两个程序的行为特征表达分别记作P和Q,其中P={p1,p2,…,pn},Q={q1,q2,…,qn},pi和qi分别是两个程序的行为特征,n值依赖于被度量的程序行为类型,当度量黄金运行时,n取15626;当度量错误行为时,n取5;当度量失效行为时,n取4.两两程序行为的相似性度量如下:
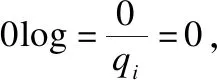
两个程序行为特征表达之间的差异性越大,D(P,Q)越大;当且仅当两者完全相同时,D(P,Q)为0.若选取的目标程序数为M,则基于上述度量可获得三个M×M的相似矩阵.
4.2 基于程序特征表达的程序分类方法
为与文献[1]进行实验对比,采用模糊聚类(Fuzzy Compactness and separation,FCS)算法分类程序行为特征[16].该算法同时考虑类内程序行为间的紧凑性和类间各行为的离散性,大大提高了聚类算法的准确性.
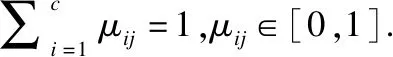
类间距离权重ηi、隶属度μij和聚类中心vi的优化如下:
(1)
(2)
(3)
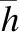
算法步骤如下:

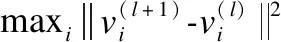
5 实验分析与讨论
实验主要探讨两个方面的问题:
1)程序黄金运行的分类方式是否同样适用于划分其错误行为和失效行为?
2)程序黄金运行的分类方式是否能有效将具有相似可靠性特征的程序划分到一类中?若结果是正面的,则该研究提供了一种以软件的失效机理来衡量软件可靠性的方法.
3)对比文献[1]的分类效果.
5.1 实验对象选取
为获得充足的实验数据,且尽可能的让其接近真实的用户场景,选取SPEC 2006作为实验对象.SPEC 2006是一组计算密集型程序,包含整型运行程序和浮点型运行程序,覆盖了解释器、编译器、游戏、隐马尔科夫模型运算等典型的计算型程序,在工业界常用来衡量系统的全面性能.以该程序集作为研究对象,在分析失效机理和可靠性方面具有更强的统计意义.
在故障类型的选取方面,与文献[1]一致,采用正交缺陷分类方法,将软件故障划分为赋值类、校验类、接口类、算法类和功能类等.采用文献[1]提出的故障分类作为实施故障注入实验的主体,故障细分类型如表1所示.
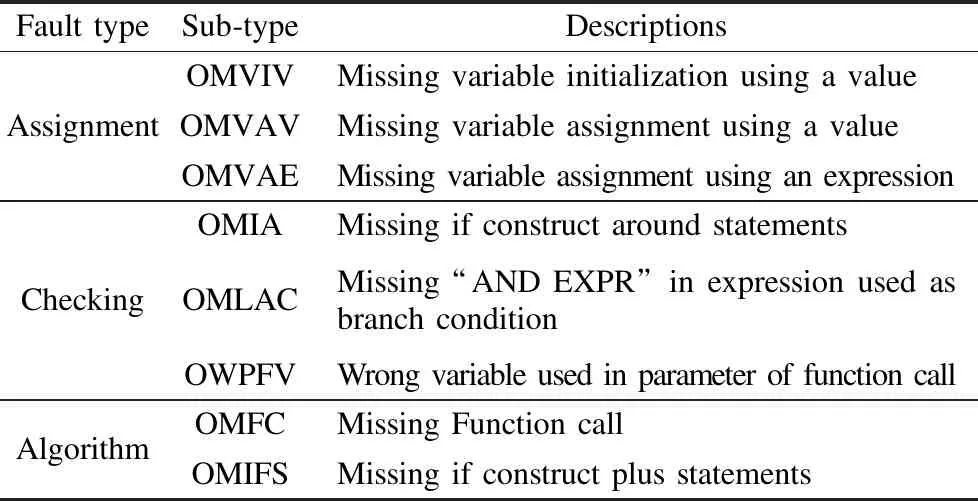
表1 ODC故障细分类型及描述Table 1 ODC sub-types and descriptions
选取12个SPEC 2006基准程序,每个程序的操作剖面为程序集中给定的输入集,即ref、test和train类.通过扫描程序的目标代码确定可注入故障的位置和类型,用以表征每个程序的故障空间分布.所选程序及其注入故障空间分布的特征如表2所示.需要说明的是,用于分类的程序以单个输入值下的程序行为特征为单位,实验中不考虑程序的具体类型,仅考虑与操作剖面相结合的特定程序行为特征,聚焦失效机理的研究,因此,分类前程序均“匿名”标识.
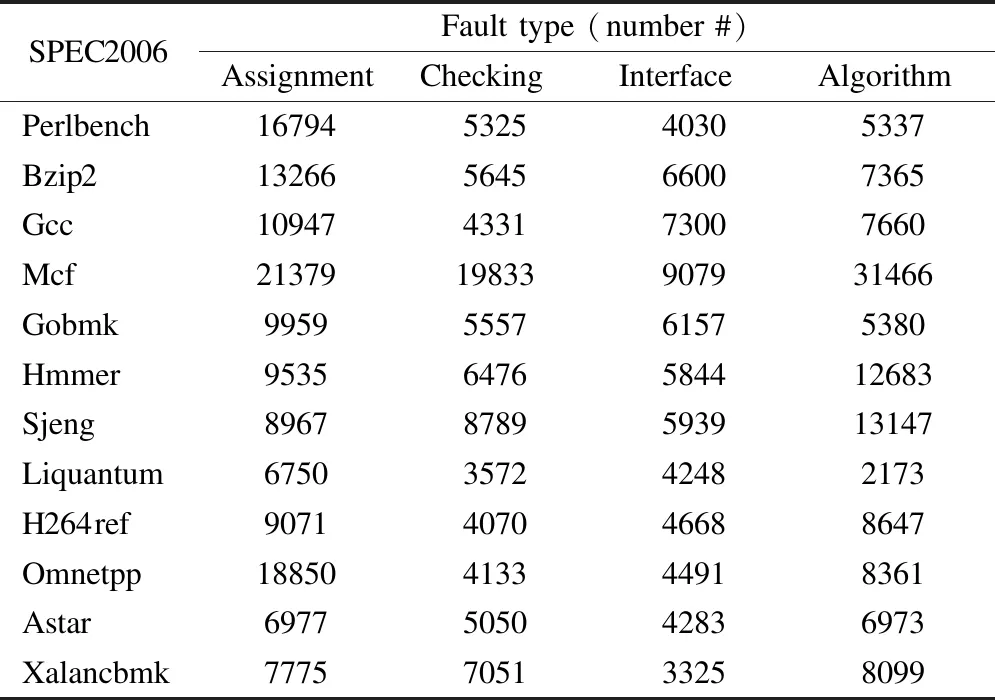
表2 SPEC 2006 基准程序的故障空间分布情况Table 2 ODC-based fault distribution for SPEC 2006 benchmark
5.2 实验步骤
步骤1.50个程序在无故障条件下运行,生成50组基准程序特征表达,即6-长子序列的频率分布;
步骤2.对50组程序实施ODC故障注入,分别收集错误行为和失效行为的特征表达,即错误和失效的频率分布;
步骤3.将黄金运行、错误行为和失效行为的特征表达分别进行聚类,得到Cluster_norm,Cluster_err和Cluster_fail,计算各类内两两程序之间的平均相似度;
步骤4.将程序的错误行为和失效行为用黄金运行的分类方法进行划分,计算各类内两两程序之间的平均相似度;
步骤5.为获取程序与可靠性相关的特征,考虑故障的时间分布特性,对程序实施以指数分布为前提的故障注入时间,并记录程序的失效时间和计数;
步骤6.将获得的程序失效按照等间隔时间计数方式对应到二维空间中;
步骤7.分别计算三种分类中程序失效分布的相似性,具体方法如下:
步骤7.1.按照Cluster_norm对程序的失效分布进行分类,计算类内两两程序之间的样本标准差,并最终算得类内全部样本的标准差平均值;
步骤7.2.按照Cluster_err和Cluster_fail分别对程序的失效分布进行分类,计算各个类内的样本标准差平均值;
步骤8.实验完毕.
关于步骤5,采用J-M(Jelinski-Moranda)模型为故障注入的假设前提,如下:
假设1.在程序中,其原本存在的故障数为N0,且为一个未知常数;
假设2.程序中的错误均相互独立,每个错误引发系统失效的概率基本相同,且失效间隔也相互独立;
假设3.在测试阶段检测到的故障均被排除,且单次排错数为1(排错时间忽略不计,且在排错时,不会引入新的错误);
假设4.程序的失效率在每次失效间隔内均为常数,数值正比于残留故障数,在第i个测试区间内:
失效率Z(xi)=φ(N0-i+1)
假设5.程序的运行方式与人们预期的方式相似.
5.3 实验结果与分析
表3展示了SPEC 2006基准程序在FGBB和BIP[1]两种程序行为表征方法的条件下,通过特定的聚类算法得到的程序黄金运行和错误、失效行为的分类结果.其中,分类质量是指,程序的故障行为和失效行为按照黄金运行的行为特征分类结果聚合,随后得到的类内各个程序间的平均相似度.由于FGBB和BIP方法采用的聚类算法基本一致,且两两程序间的相似度度量方法也相同,那么,类内行为的平均相似度越高,说明“黄金运行”的行为特征提取机制越优.
FGBB方法选取6-长子序列,而BIP方法选取7-子序列(根据文献[14]中的实验分析获得的子序列最优值),两者均把程序分为3类.从表3可以看出,FGBB在黄金运行的行为分类上取得的类间相似度略高于基于BIP方法的黄金运行.针对错误行为的分类结果中,FGBB方法在每个故障细分类型下都表现出较高于BIP方法的分类质量,即每个类间程序的错误行为更加近似.以OWPFV故障类型为例,它表示函数参数被设置了错误的值,由于FGBB方法是基于首错误的行为特征表达,其BRETS和ARETS两个程序状态可以提前检测到由于函参导致的中间变量或跳转条件上的错误.因此,对于函数嵌套调用和条件语句频繁执行的程序,FGBB方法对错误的检测更加敏感.
从失效行为的分类结果看,两种方法不分伯仲.在FGBB优于BIP的几组故障细分类型中,多以与函数相关的故障为主,如OWPFV、OMFC和OMIFS.这进一步说明,为函数返回前后定义两种不同的程序状态类型,把函参、返回值及中间变量作为判断程序错误/失效的条件之一,可以更准确和高效地定位程序的脆弱点,提升程序的容错能力.
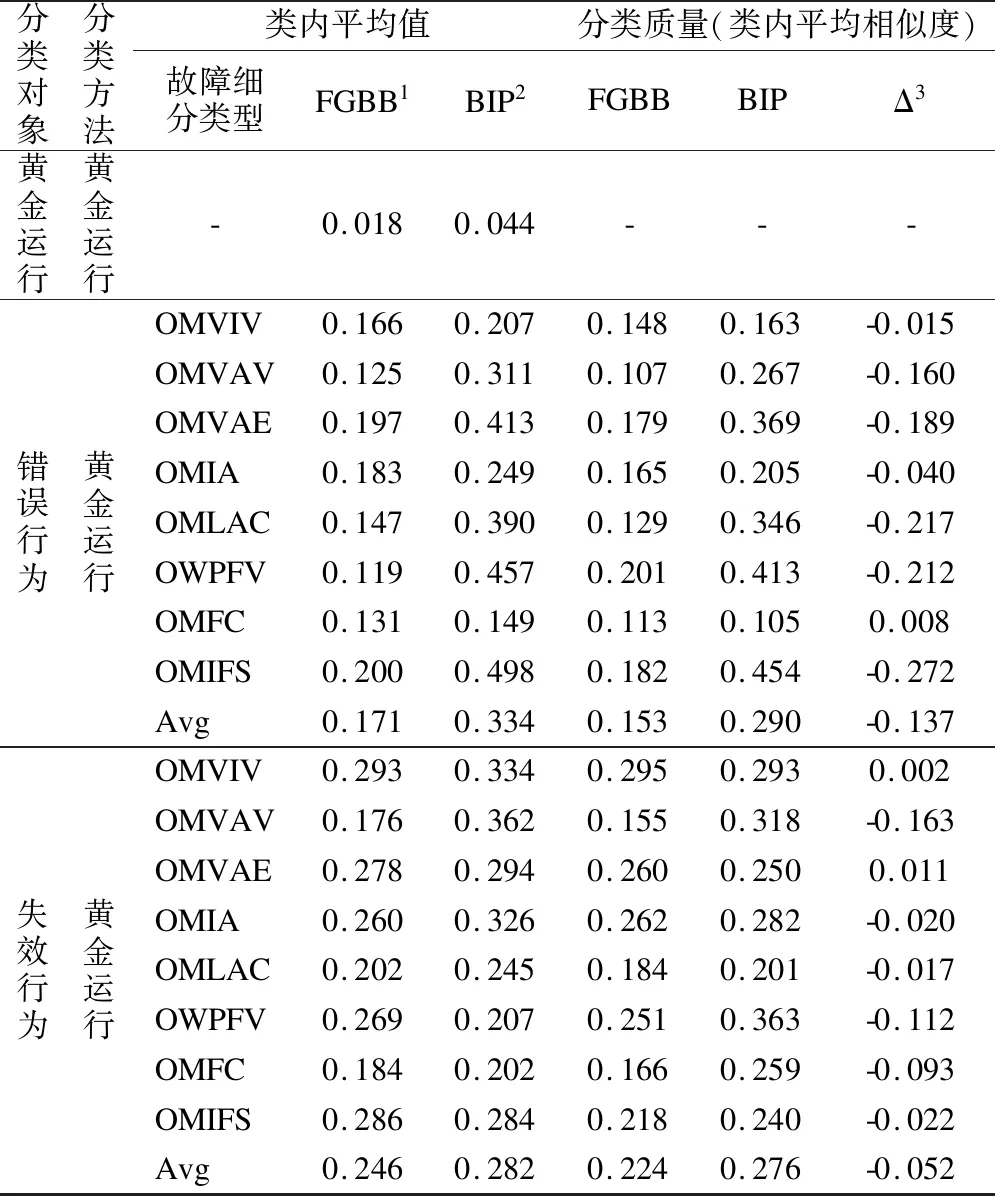
表3 基于黄金运行行为的程序故障/失效行为的类内平均相似度Table 3 Intra-cluster average similarity of error/failure behavior based on golden run behavior
1FGBB表示基于本文方法提取程序状态并完成行为分类
2BIP表示基于文献[14]方法提取程序状态并完成行为分类
3Δ为FGBB和BIP方法获得的错误/失效行为的类内平均相似度的差值,即分类质量
图1展示了FGBB方法和BIP方法在分类质量上的直观统计.可以看出,绝大多数错误行为和失效行为在FGBB方法的分类过程中可以更准确地被聚合,尤其是针对错误行为,其黄金运行的行为特征基本能揭示不同ODC细分故障类型下的错误行为发生规律,对故障具有较为敏感和准确地提前判断和定位.
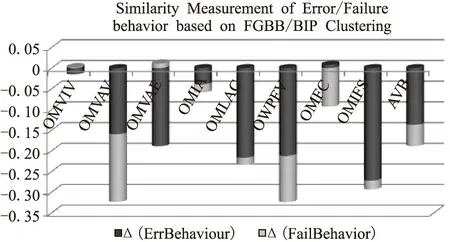
图1 基于FGBB/BIP方法的分类质量对比Fig.1 Similarity measurement of error/failure behavior based on FGBB/BIP clustering
为探讨程序结构与其错误和失效行为之间的关联,进一步分析黄金运行特征中的高频状态序列.图2(a)-图2(c)展示了基于FGBB方法聚类得到的三类程序行为的状态序列频度分布.在图2中,横坐标为15625个不同的状态序列,分别以0-4编号对应的状态类型,即UJS、CJS、CLS、BRETS、ARETS.由于横坐标密度较大,频度较高的状态序列实际为一簇值,图2(a)-图2(c)中标号主要标注频度最高的状态序列.
不同分类中的高频状态序列特征明显.Cluster 1中几个高频序列为111111、*111**、343434.其中,111111和*111**说明程序中的条件判断多且连续,结合程序结构特征发现,其中包含大量循环结构,如程序Liquantum和H264ref;而343434则说明程序中含有较多嵌套函数,如程序Gobmk.Cluster 2中高频状态序列有011111、122223、211111等.其中,011111说明条件判断语句较多,而122223为明显的函数嵌套调用过程,211111说明子函数中含有大量循环结构执行,程序Xalancbmk属于这种类型.同理,Cluster 3的程序大多具有执行大量循环结构的特征,如程序Gcc,以及较多选择结构的Astar和Bzip2程序.

图2 基于FGBB方法的状态序列谱系特征Fig.2 Status sequence characterization based on FGBB
为了对比基于BIP方法的程序分类情况,根据文献[14],收集如表4所列出的两种方法在每一类中的最高频的三种程序状态序列.可以看出,每类中的典型行为特征在两种方法中均有比较一致的体现,如类1中均包含拥有大量循环结构的程序Liquantum和H264ref,和函数嵌套执行较多的程序Gobmk;类2集中包含执行了大量循环体和函数调用的程序行为,如Xalancbmk;类3中的程序在执行过程中多以循环和选择结构为主,如程序Gcc,Astar和Bzip2等.
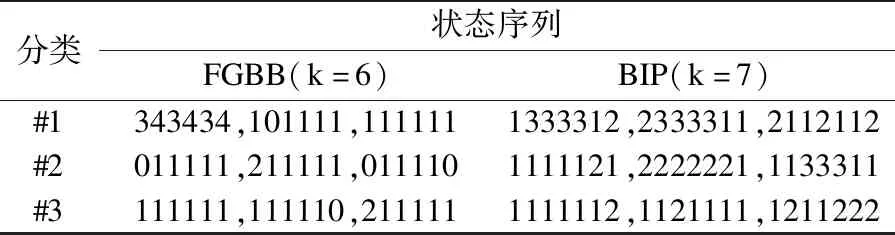
表4 基于FGBB与BIP方法的高频状态序列统计Table 4 Sequence occurrence of top-3 frequency for FGBB and BIP method
基于上述分析可知,FGBB方法与BIP方法一样,均能以其状态序列及频率分布表征程序的结构特征及其运行时的行为特征.在利用黄金运行对程序的错误和失效行为进行归类的过程中,FGBB方法表现出更优的表征错误行为并提取其行为特征的能力,尤其是在对函数调用过程中的程序故障行为的表征和检测,可以做到在状态序列变更并造成更严重的程序运行偏差之前表征出相应的错误,与文献[1]对首错误的研究结果一致.此外,在针对失效行为的分类方面,实验结果与文献[14]基本一致,但在针对函数的ODC细分故障类型下的判断和分类更加准确一些.文献[1]也提出,程序控制流的改变对程序的运行状态有较大影响,且控制流改变引发程序失效的概率通常较高.因此,及时监测并确保程序运行时的控制流的正确性十分重要.FGBB方法正是基于上述思想实现了对程序行为的特征表达,从实验结果可以看出,在对故障条件下的程序行为表征和分类质量方面,FGBB方法较BIP方法略优.
6 结束语
软件可靠性是代码量、算法复杂度的函数,本文从“故障触发错误+错误导致失效”的过程出发,在文献[1]对“首错误”研究基础上开展后续工作,探讨与软件可靠性相关的特征行为分类,并与文献[1]做类比.结果表明,在针对错误行为的分类方面,由于FGBB方法以软件“首错误”定义状态序列,得到的基于ODC细分类型故障下的程序错误行为的各异性比文献[14]的BIP方法略优.本文研究工作的意义在于,能够像硬件一样,将软件的固有特征体现在其运行行为中,使得对软件行为的分类可以类比硬件,即基于某种“失效机理”,这将有利于软件可靠性评测的进一步展开.

