水文序列趋势及形态变化的表征方法

张姝琪，张洪波,2，辛 琛，南政年，李哲浩

(1.长安大学环境科学与工程学院，陕西 西安 710054； 2.长安大学旱区地下水文与生态效应教育部重点实验室，陕西 西安 710054； 3.陕西省江河水库管理局，陕西 西安 710018)

近年来，受气候、土地覆盖等自然要素变化和人类活动扰动的影响，流域的水文过程发生变异，水文序列不再满足一致性要求，导致变化环境下基于一致性假设的水文频率计算方法备受质疑[1-3]。在水文序列非一致性的研究方面，数据序列的趋势变化检验一直是一项重要的研究内容，其对水文分析、模拟、预测以及水文时空变化规律都有着关键性影响，同样也对变化环境下流域水资源管理与决策具有深远意义[4]。

现阶段，识别水文序列趋势变化的方法有很多，如回归分析法[5]、Spearman法[6]、滑动平均法[7]等。其中最常用的是回归分析法，常用的回归类型有一元回归、多元回归、指数回归、对数回归、多项式回归等[8]。回归分析法也存在一定的不足，如当水文序列变化的无序性较大时，回归系数偏小，趋势特征不明显，将会难以判断。为此，有学者将Mann-Kendall非参数检验法(M-K法)引入气象水文序列的趋势分析中，用以判断气象水文序列发生的趋势性变化[9-10]。M-K法是国际气象组织推荐的一种判别气象水文等自然变量趋势变化的方法，由于不要求分析样本遵从一定分布，且不受个别异常值和缺失值的干扰，故在气象水文领域应用十分广泛。此外，M-K法原理简单，计算简便[11]，能够很好地描述气象水文数据序列的趋势特征[12]，并在以往的实践中已取得很好的应用效果，如邸择雷等[13]基于呼伦贝尔草原新巴尔虎右旗1958—2016年的气温和降水数据资料，应用M-K法得出了年平均气温显著上升、降水不显著下降的趋势检验结论。曹静等[14]以科尔沁沙地西部为研究区域，利用1981—2016年气象资料，使用M-K法对蒸发皿蒸发量的变化进行了趋势研究，结果表明，在过去36年里该地区的蒸发皿蒸发量呈显著下降趋势。李佳秀等[15]以新疆地区为研究对象，使用M-K法对气温和降水资料进行分析，结果表明近50年来，降水呈增长趋势。张岩等[16]采用M-K法分析了1957—2012年三江源区径流的变化趋势，结果表明47.3%区域的径流变化趋势不显著。

与许多气象变量不同，水文变量由于受到人类活动的高强度扰动，不再呈现纯粹的递增或递减趋势变化，而是更趋多元化变化，通过文献梳理，可大体将这种变化总结为加剧、抵消以及紊乱3种情形。所谓加剧，指持续性的高强度人类活动使原本较为显著的趋势变化更加严重，如河道阶梯性取水引发的下游径流量的持续性衰减；抵消，指人类活动使原本较为显著的水文趋势变化变缓或消失，如枯水期河川径流日益趋于干涸，但是上游建库后丰水期的水被调蓄至枯水期，导致枯水期水量增加，原有径流序列中的枯水减少趋势随之不显著甚至消失；紊乱，指人类活动使得原本显著的水文趋势变化趋于无序和复杂，原本单调的趋势变化开始震荡，表现出愈来愈强的非线性特征，导致很难确定水文序列的整体走向。

众所周知，在高强度的人类活动影响下，水文要素发生了不容忽视的变化[17]，水文序列不再是平稳序列，趋势变化的特征也日趋复杂，不再是简单的线性关系。尽管前文所提到的M-K法具有不需要样本服从某一分布且不受异常值干扰等优势，但受其原理(秩次)制约，检验结果始终与秩的大小变化息息相关[18]。当两个水文序列恰好具有相同的秩次关系时，其M-K检验结果必定一致，从而获得两个序列具有相同的趋势特征的结论。事实上，两个序列可能还存在一些有关趋势变化的个性化信息或其他重要形态信息，因为M-K检验而被丢失或未能体现。可见，M-K法在识别序列趋势变化的细节特征或者说形态变化上尚有不足。此外， M-K法的统计检验值仅表征序列的秩次关系，并不能用于实际水文序列的空间对比分析，导致M-K法在空间应用的拓展上一直举步维艰。为此，本文基于M-K法提出一套水文序列趋势及形态变化分析的指标体系与方法，通过提取水文数据序列的趋势及形态特征，可实现水文序列变化的细节刻画和空间对比分析。本文以渭河流域为研究区开展案例研究，以验证指标体系方法的适用性。

1 研究区概况及数据来源

渭河流域西起鸟鼠山，东至潼关，北起白于山，南至秦岭，流域范围为北纬33°50′～37°18′、东经104°00′～110°20′，面积13.48万km2[19](图1)。渭河干流全长818 km，平均比降1.3‰，占黄河流域面积的18%，是黄河的第一大支流[20]。流域地处黄土高原南缘，秦岭北麓，位于干旱地区与湿润地区的过渡地带[21]。流域的降雨时空分布极不均匀，年均降雨量介于200～900 mm之间，且年内、年际变化较大，导致流域内的水资源分布亦呈现时空上的差异性变化[22-23]。渭河流域是通往西北、西南的咽喉要地，也是我国重要的粮棉油产区和工业生产基地之一。特殊的地理位置使其在西部大开发战略中具有重要地位，其流域水资源状况对黄河水资源的丰枯变化和开发利用具有重要影响[24]。然而随着大规模的工业、农业生产活动对水资源需求的不断增大，渭河径流持续缩减，趋势变化强烈且日趋复杂，已引发下游河道淤积、水土流失严重、洪涝灾害突出、水污染严重等一系列生态环境问题，导致流域生态环境系统遭到破坏，生态灾害频繁发生[25]。因此，了解流域内径流序列的形态变化特征，尤其是趋势变化，不仅可科学地认识变化环境下渭河流域的水文演变规律，也对指导区域未来的经济布局以及水资源安全保障有着极其重要的意义。

图1 渭河流域水系及水文站分布图

为更好地描述渭河流域径流趋势变化的空间差异性，本文选取渭河干流上的北道、林家村、魏家堡、咸阳、华县5个干流水文站和张家山、状头站2个支流水文站的实测年径流资料作为基础数据资料。资料长度统一为51年(1959—2009年)，资料来源于黄河水利委员会水文局。

2 研究方法

2.1 去趋势预置白

众所周知， M-K法的使用前提是检验数据之间相互独立，然而很多水文数据并不满足该要求，故本文采用去趋势预置白(trend-free pre-whitening，TFPW)方法[26-27]对序列进行去一阶自相关处理，从而使待检序列满足M-K法的使用要求。具体步骤[28]为：设一待检序列为Xt(t=1, 2, …，n，n为序列长度)，则有

Yt=Xt-βt

(1)

Yt′=Yt-γYt-1

(2)

Yt″=Yt′+βt

(3)

(4)

式中：Yt为扣除趋势后的残余序列；Yt′为去除自相关项后的独立白噪声序列；Yt″是经过TFPW处理后得到的新序列；β为待检序列的坡度，可通过Theil-Sen法[29]即式(4)计算；γ1为Yt的自相关系数，阶数因序列差异而有所不同，常规计算中多选一阶系数。需要注意的是，如果γ1足够小，可认为Yt是一个独立序列，即可不处理，直接使用M-K法进行趋势检验，否则需要带入式(2)(3)计算，并最终将Yt″代入M-K检验。

2.2 M-K趋势检验

M-K法已在径流、气温、降水等气象水文要素的序列趋势检验上[30-32]广被认可。

先定义检验统计量S：

(5)

式中sign()为符号函数。当(Xi-Xj)<0、≥0时，sign(Xi-Xj)分别为-1、0或1；当检验统计量S≥0、<0时，标准化统计量Z可计算：

(6)

式中Z为正值表示上升趋势，为负值表示下降趋势。Z的绝对值大于等于1.96时可认为其通过了置信度为95%的显著性检验，即趋势显著。

梳理M-K法的检验原理，不难发现M-K法主要是通过秩将非正态分布的原序列转化为服从正态分布的秩序列，并由此采用统计检验方法判断序列的趋势性变化。从应用范围上看，M-K法因为假设前提较少，故其应用更广，对未经处理的数据所得的检验结果也更加可信。然而，M-K法也存在一定的不足。M-K法虽然可以给出一个定量化的趋势统计量，即在整个时域上对数据序列进行趋势判断是行之有效的，但并不能区分具有相同Z值的数据序列趋势及形态之间的差异性变化。水文工作者或流域管理人员依据同一流域不同站点径流资料的M-K检验结果，并不能准确了解径流序列的变化，对于序列中某一时间段的趋势行为或者是哪些变化引起整个时域上的趋势演变，也无法有效掌握。鉴于此，本文提出构建一套表征趋势及形态变化的指标识别体系与方法来弥补M-K法在趋势分析及形态化细节识别上的不足。

尽管水文序列形态变化形式众多，且可能存在掩蔽问题，但如果能通过指标体系宏观描述序列的这些趋势和形态变化特征，则可极大程度地帮助读者对序列变化有一个相对直观的了解与认识，并可通过指标值的差异较为准确地判别不同序列之间的差异性。基于以上分析，笔者结合M-K法，提出了表征水文序列趋势和形态变化的指标体系，主要包括：①M-K统计量Z值，反映待检序列的总体趋势；②拟合抛物线系数a，反映待检序列趋势形态变化的具体表现形式；③平稳序列(待检序列去除趋势成分)的集中度与集中期，反映径流波动的能量分布及最大能量分布的位置；④方差序列拟合的抛物线系数a′，描述径流波动在时域上的渐变性特征。具体指标计算方法如下：①使用TFPW方法对实测水文序列进行去自相关处理，得到满足M-K法应用假设的待检序列；②对待检序列进行M-K非参数趋势检验，得到序列在整个时域上的总体趋势变化指标，即Z值；③对待检序列进行二次拟合，得到拟合方程y=ax2+bx+c中的抛物线系数a，通过a可判断趋势形态变化的非线性表现形式；④对待检序列作趋势成分剔除处理，得到平稳序列，并对其集中度、集中期进行统计计算，揭示径流序列波动的能量分布特征；⑤以平稳序列为基础，通过滑窗计算，得到均方差序列，并对其进行抛物线拟合，得到抛物线系数a′，表征径流序列波动的渐变性特征。

3 结果分析

3.1 指标计算

以咸阳站和状头站实测径流序列为例，阐述各指标的计算过程。

a. M-K统计量Z值与抛物线系数a。将咸阳站及状头站的实测径流序列代入TFPW前置处理程序进行自相关性剔除，得到新的径流序列，即待检序列，其偏自相关性统计检验结果见图2。由图2可知，两站实测序列经自相关剔除处理后，原序列中的显著自相关性较好地被控制在可接受范围内。

图2 咸阳站和状头站径流序列TFPW处理前后的偏自相关性检验结果

然后，对待检序列实施M-K趋势检验和二次拟合(抛物线)计算。M-K检验结果显示咸阳站及状头站待检径流序列的统计量Z分别为-4.548 4和-1.840 3，即咸阳站待检序列通过了95%的显著性检验，这表明咸阳站的年径流序列在整个时域上表现为显著的下降趋势，而状头站待检序列为不显著下降趋势。将二次拟合结果与径流序列一并绘制于图3中，可发现二次拟合曲线也表明序列呈现为下降趋势。其中，咸阳站及状头站待检序列的二次拟合抛物线系数a分别为0.0171和-0.0038，数值均较小，即为不显著的凹减和凸减形态。就a值来看，咸阳站年径流序列呈现先减后增的非线性趋势，而状头站年径流序列呈现先增后减的非线性趋势。

b. 均方差序列抛物线系数a′。由M-K法的检验效能分析可知，M-K趋势检验对序列的离散程度或分段离散特征无法有效表征，使其在形态变化上的指代意义有所欠缺。为了反映序列形态变化中的离散特征(方差渐变性和能量分布特征)，本文采取滑窗的方式对剔除趋势成分的平稳序列逐段进行方差统计，得到一个连续的均方差序列，并对均方差序列进行二次拟合，获得均方差序列的抛物线系数a′，并以此描述序列方差的渐变性特征，所得结果见图4。由图4可知，咸阳站及状头站径流序列的a′分别为0.017和0.000 7，这表明两站的方差序列呈不显著的凹减型变化，且咸阳站的方差曲率大于状头站。

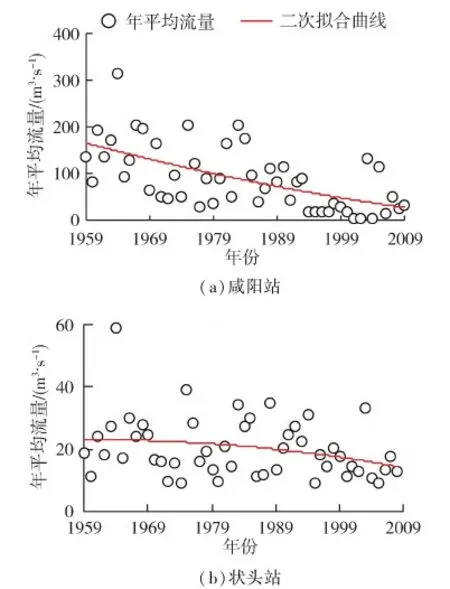
图3 咸阳站和状头站年平均流量序列及其二次拟合曲线

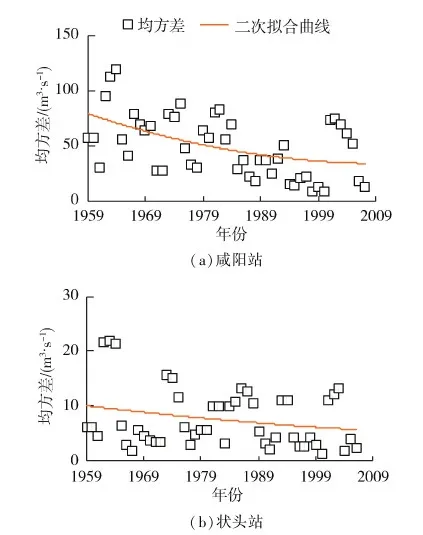
图4 咸阳站和状头站均方差序列及其二次拟合曲线

c. 集中度与集中期。方差序列的抛物线系数a′主要体现了年径流序列在时域上的非线性渐变波动特征(方差渐变性)，如凸增型、凹减型等，但是并不能体现波动变化的能量分布。汤奇成等[33]在研究年径流量在一年中的分布情况时，曾借鉴表示降水量年内分配的向量法，提出用集中期(concentration period)和集中度(concentration ratio)两个概念来反映径流年内分配的各种特性，效果令人满意，Zhang等[34]也利用集中度集中期反映了黄河流域降雨在年内的分布情况。本文将借鉴集中期和集中度的概念来描述年径流波动的能量分布情况。这里，方差集中度的大小主要反映一个序列的方差变化是均匀分布还是集中在某一年或某几年。方差集中度越大表示该序列径流波动的能量越集中；反之，序列的波动能量更趋分散或平缓。而方差集中期则指示了最大的波动所对应的年份，即径流波动的能量极值点。

集中度、集中期的分析对象为剔除趋势成分的平稳序列。具体计算步骤如下：①将整个研究时段认为是一个圆周，可分为N份，N表示数据序列的总个数；②每一个数据位置(年)相对应的角度为360°/N；③根据文献[33]中所列公式，进行Matlab编程计算。由计算结果可知，两站方差序列的集中度均小于33%，说明方差变化分布较为均匀，且状头站更显著，这与图4所展示的结果是一致的。在能量极值点上，咸阳站出现在1967年，而状头站出现在1982年，表明这两个时间段径流序列能量波动较大。

d. 综合分析。以咸阳站年径流序列的趋势及形态变化特征为例，开展综合分析。序列主要特征为：①整个序列呈现显著的减小趋势(M-K统计量Z为-4.548 4，且绝对值大于1.96)；②减小的形式为不太显著的凹减型(实测序列抛物线系数a为0.0171)；③径流波动在时域上呈现凹减型，即波动存在一个先减小后小幅增加的过程(方差序列抛物线系数a′为0.017)；④径流波动能量较为分散，即波动相对平稳(集中度小于33%)，且波动的高值区主要集中在1967年附近，综合两种信息以及其下降趋势，认为在1967年附近应该存在一个大的向下跳跃。

当获取了这些形态变化特征后，可根据这些特征所携带的信息，大体勾勒所描述的径流序列的趋势及形态变化，并对径流序列的表现形式给出定性的分析。以咸阳站为例，具体过程见图5。

由特征①、②可勾勒出咸阳站径流序列的整体趋势变化(图5(a))；由特征③可勾勒径流序列的波动应呈现为先强后弱，再微弱渐强的过程(图5(b))；由特征④可修订图5(b)，即除先强后弱，再小幅渐强的过程外，还应体现整体波动差异不是特别大，且在1967年附近存在径流波动的高能区的特点(图5(c))。最后将图5(a)和图5(c)相融合，可获得整体的重构结果(图5(d))。

同理，可重构状头站径流序列的整体趋势变化，如图6所示。需要说明的是，由于只是示意图，因此数据关系可能不完全闭合。将其与图3中的咸阳站和状头站的实测年径流序列进行对比，可发现重构的示意性序列能较好地体现原序列的趋势与形态特征。可见，应用本文所提出的指标体系(Z，a，a′，集中度，集中期)，可较好地描绘原系列的趋势与形态特征，并将其量化，读者可借由各指标值宏观了解掌握实测系列的趋势与形态变化。

图5 基于指标特征信息的咸阳站径流序列趋势与形态变化特征重构示意图

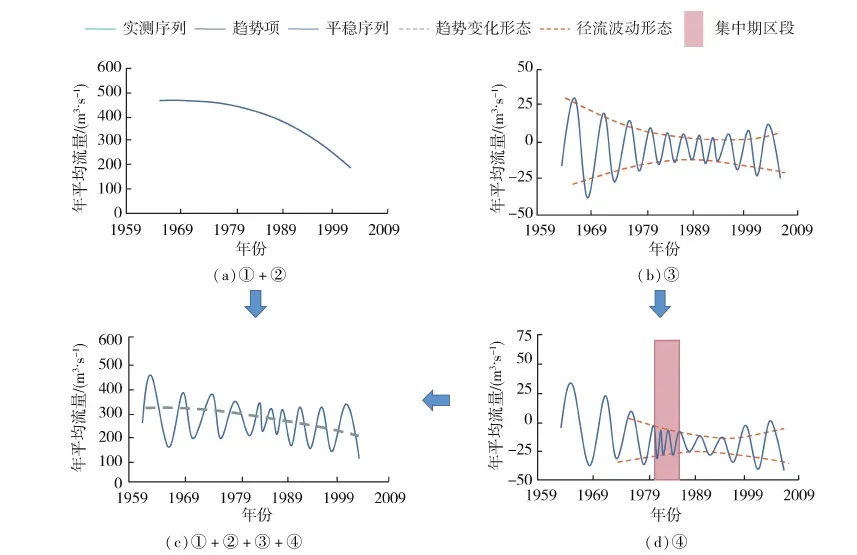
图6 基于指标特征信息的状头站径流序列趋势与形态变化特征重构示意图

3.2 指标体系在流域空间分析中的应用

为验证以上指标体系的空间适用性，本文进一步分析了渭河流域其他各站点的序列趋势与形态变化，并进行了空间对比分析。

应用上述方法对其他站点进行指标计算与分析，所得结果见图7～9。

由图7可知，TFPW方法有效消除了各站点序列中自相关性的影响，可满足M-K法应用假设。将待检序列分别进行M-K检验，结果分别为-3.752 5、-4.759 6、-4.970 8、-5.133 2、-3.443 8，由此可知，5站径流序列均显示出显著的下降趋势。图8给出了各站点序列的二次拟合结果。由图8可知，M-K检测结果与二次拟合结果基本一致，a系数分别为0.013 9、0.018 4、0.013 8、-0.004 2、-0.022 6，即华县、魏家堡及林家村站呈现凹减型下降趋势，而北道站、张家山为凸减型下降趋势变化，除张家山站外，其他站点非线性变化均不显著。

图7 不同站点年径流序列TFPW处理前后的偏自相关性检验结果

图8 不同站点年径流序列及其二次拟合曲线

图9 各站均方差序列及其二次拟合曲线

图9显示了各站的方差序列及其二次拟合曲线，其抛物线系数a′分别为0.0161、0.018、-0.0016、0.009、0.0047，其方差的变化依次是凹减下降末尾渐平、快速凹减下降末尾渐升、凸减、凹减末尾渐升、缓慢凹减。

各站径流序列的集中度和集中期统计结果见表1。从表1可知，除华县站外(集中度大于70%)，各站的径流波动均较为平稳(集中度小于20%)。其中，华县站的集中度最大，张家山站最小，其结果也与方差变化的实际情况(图9)较为相符。而集中期则主要分布在4个时段，即1970年、1963年、1973年及1960年。

表1 渭河流域各站集中度和集中期

最后，依据各站不同指标所指代的信息进行综合分析，并与实际径流序列进行对比，结果见图10。图10显示了华县、魏家堡、林家村、北道、张家山5个水文站实测水文序列及形态变化，绿色区域表示该序列的集中期区段，即径流波动最大的位置。由图10可知，5个指标较好地反映了实际水文序列中的形态变化，由此可以看出本文所提出的方法是行之有效的，指标体系可较好地体现原序列的趋势及形态变化特征。

鉴于以上定量化指标，将渭河流域7个站点的指标值分别统计于表2中，可以发现渭河流域各站点径流序列均表现为较为明显的下降趋势(状头站为不显著下降)，但其趋势形态略有不同，呈现差异性的非线性特征。另外，序列波动特征也不一致，在方差渐变性及能量分布上有一定区别。通过结果的对比，可发现本文提出的面向趋势和形态变化的指标体系是切实可行的，能够分析出序列趋势及形态特征的差异，有利于全面认识渭河流域径流序列的变化，实现同一流域不同站点或不同流域水文序列之间的比较与分析。

图10 渭河流域5站年径流序列及形态变化分析

表2 渭河流域上游至下游及支流7个水文站指标值

4 结 论

a. 基于秩的M-K法因检验机理限制，对序列的形态变化表征不够充分，可能遗漏重要细节趋势信息，从而影响对水文序列规律的认识。

b. 通过表征指标体系中的5个指标(Z、a、a′、集中度、集中期)能简单有效地重构示意性水文序列，实现对序列趋势及形态变化的细致刻画与表征。

c. 借助指标体系的定量化优势，可以实现同一流域不同水文站点或不同流域水文站点间的序列对比分析。

目前研究对象仅局限于渭河流域，对于该方法适用范围的确定还需进一步补充验证。同时，本文提出的集中期仅指示序列波动最大点的位置，对于其波动方向以及影响范围尚无法准确界定，仍需进一步完善。