考虑钢筋锈蚀的渡槽时变可靠度分析
常 佳, 祝彦知
(1.中原工学院 建筑工程学院, 河南 郑州 450007; 2.中原工学院 建筑设计研究院, 河南 郑州 450007)
渡槽是水工建筑物的重要结构形式。渡槽结构长期处于潮湿的工作环境,常因钢筋锈蚀导致混凝土保护层开裂而达不到设计的使用年限。因此,在渡槽耐久性分析中,考虑钢筋锈蚀导致的渡槽结构失效,具有重要的实际意义。钢筋锈蚀导致的渡槽混凝土保护层开裂、剥落等耐久性问题在我国较为普遍。在渡槽结构劣化随时间变化规律不明的情况下对渡槽进行维护,很难避免大量人力物力的浪费。因此,研究钢筋锈蚀导致渡槽结构耐久性下降问题很有必要。
此前,国内外许多学者在这方面做过研究。赵国藩等根据概率论提出的结构可靠度理论,奠定了工程可靠度分析基础[1]。牛荻涛等利用电化学原理,在结构碳化的基础上建立了钢筋锈蚀量估计的预测公式,并给出了钢筋混凝土结构耐久性的可靠度公式[2]。潘洪科考虑影响钢筋混凝土耐久性的综合因素后,给出了混凝土碳化与钢筋锈蚀的估计公式,并建立了结构寿命预测模型[3]。FRANGOPOL等基于可靠度理论开展了结构全寿命成本研究[4]。解伟等将可靠度理论引入渡槽耐久性分析,采用可靠度理论对涵洞式渡槽进行了系统分析[5]。陆春华等通过氯离子扩散和裂缝宽度模型,采用时变可靠度对钢筋混凝土进行了全寿命成本预测[6]。李扬等采用模糊可靠度算出的混凝土裂缝宽度可靠度指标,对工程实践有一定的参考价值[7]。祝彦知等采用模糊时变可靠度理论对渡槽碳化深度进行研究,并基于渡槽碳化深度预测了渡槽的寿命[8]。林辉等基于验算点法,采用时变可靠度对桥梁寿命进行了预测[9]。张璐等基于钢筋锈蚀深度理论,考虑变量模糊性后给出了混凝土结构的耐久性可靠度,但其未考虑可靠度的时变性[10]。上述研究在评定结构耐久性时,很少针对渡槽结构进行钢筋锈蚀破坏的计算,即使涉及计算,也多数采用一次二阶矩法,计算不够精确。因此,本文考虑结构劣化过程中的时变性,拟分别采用中心点法与Monte-Carlo法,通过Matlab软件计算渡槽钢筋锈蚀引起混凝土保护层开裂的可靠度指标。
1 结构可靠度分析原理
结构可靠度分析的依据在于结构是否达到极限状态。结构极限状态可分为承载力极限状态和正常使用极限状态[11]。设结构使用状态的影响因素为Xi(i=1,2,…,n)向量(它是一个随机变量),则可用Z=g(X1,X2,…,Xn)表示结构的功能函数,且有
(1)
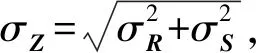
若R与S不服从正态分布,则需对其进行当量正态化。例如,R与S服从对数正态分布,即lnR与lnS服从正态分布,可在极限状态方程中用lnR与lnS代替R与S,以便进行计算。
2 基于钢筋锈蚀量的时变可靠度计算
2.1 钢筋锈蚀量
混凝土中的钢筋锈蚀属于电化学腐蚀,钢筋产生锈蚀的前提是钢筋表面的钝化膜遭到破坏[2]。由文献[12]可知,钢筋锈蚀量推导如式(2)-式(5)所示。考虑碳化残量的存在,一般认为,在保护层未碳化到钢筋表面时钢筋已开始锈蚀。钢筋开始锈蚀的时间为:
(2)
式中:c为混凝土保护层的厚度;Kc为混凝土保护层的碳化速度。
(3)
式中:Kel为地域影响因子;Kei为室内外影响因子;Kt为养护时间影响因子;fcuk为混凝土标准抗压强度。
钢筋锈蚀除了与保护层的厚度有关,还与空气的相对湿度、氧气在混凝土中扩散的速度、钢筋的半径、锈蚀的时间等因素有关。根据菲克第一定律,氧气在混凝土中的扩散速度为:
(4)
综上所述,钢筋锈蚀量公式可表示为:
(5)
式中:PRH为空气相对湿度大于钢筋锈蚀湿度的概率;r为钢筋半径;t为钢筋锈蚀时间。
2.2 钢筋锈蚀极限状态方程
分析式(5)可知,空气相对湿度大于钢筋锈蚀的概率、氧气在混凝土中的扩散速度、钢筋的半径、保护层的碳化速度及钢筋锈蚀时间,均对钢筋的锈蚀量有影响。根据大量数据统计,这些因素都是服从正态分布的,钢筋锈蚀量公式服从对数正态分布。研究钢筋锈蚀量W(t),相当于研究结构的外在作用S。大量的研究表明,结构锈蚀开裂时钢筋的极限锈蚀量Wcr也服从对数正态分布。可将钢筋极限锈蚀量Wcr对应于结构抗力R。Wcr(即变量x)的密度函数为:
(6)
式中,μ和σ分别为极限锈蚀量对数lnWcr的平均值与标准差。
根据式(1)可建立钢筋锈蚀的极限状态方程,即
Z=g(Wcr,W(t))
(7)
Wcr的值可根据日本学者森永繁提出的计算公式求得,即
(8)
2.3 钢筋锈蚀量时变可靠度的计算方法
2.3.1 中心点法
从以上分析可知,钢筋锈蚀量服从对数正态分布。因此,钢筋锈蚀量 (即变量z)的概率密度函数可表示为:
(9)
式中,μw1(t)与σw1(t)分别为锈蚀t年时钢筋极限锈蚀量对数lnWcr的平均值函数和标准差函数。
将式(9)当量正态化,可得μw1(t)与σw1(t)的计算公式,即
(10)
(11)
钢筋锈蚀量W(t)的变异系数函数为:
(12)
式中,μw(t)、σw(t)分别为钢筋锈蚀量W(t)的平均值函数、标准差函数。
当采用式(5)来估计μw(t)、σw(t)时,考虑到碳化速度等因素存在误差,计算模型应乘以模型不定系数,即
(13)
式中,αw为计算模型不定系数。
根据误差传递关系,W(t)的平均值函数μw(t)及标准差函数σw(t)又可分别表示为:
(14)

(15)
式中,μαw、σαw、μKc、σKc分别为计算模型不定系数的平均值和标准差、碳化速度的平均值和标准差。
通过式(6)(7)(14)(15)便可求出基于中心点法的结构失效概率P(A1)。其对应的可靠度为:
β1=Φ-1[1-P(A1)]
(16)
2.3.2 Monte-Carlo法
对式(5)中所有自变量进行n次满足各变量概率密度分布的随机抽样,将抽样结果一组组地代入式(7),即可求得基于Monte-Carlo法的结构失效概率P(A2)。其对应的可靠度为:
β2=Φ-1[1-P(A2)]
(17)
3 实例计算与分析
本文以张金U型渡槽为例,分别采用中心点法与Monte-Carlo法对其进行计算分析。张金U型渡槽位于河南省济源市,于1971年修建完成,至今已运行40多年。2018年对该渡槽进行了全面检测,现场检测到渡槽保护层厚度为5 mm,槽身钢筋直径为14 mm,混凝土的强度等级为C20。根据检测结果与相关资料可列出表1所示的计算所需参数。

表1 计算所需参数
采用中心点法与Monte-Carlo法分别计算钢筋混凝土渡槽结构因钢筋锈蚀而失效的概率P(A1)、P(A2)与可靠度β1、β2。计算结果如表2所示。
当普通建筑物因钢筋锈蚀开裂的失效概率大于0.5,或可靠度小于0时,可以认为其结构已处于失效状态[12]。在2018年检测时,发现渡槽钢筋有一定程度的锈蚀,部分钢筋裸露在外,此时渡槽处于危险状态。表2数据显示,对应于第47年,采用中心点法计算的可靠度为-0.047 2,采用Monte-Carlo法计算的可靠度为-0.272 8。采用两种方法算出的可靠度均小于0,证明了计算模型的正确性。从表2还可以看出,渡槽早在运行40年左右时已到达失效状态。基于可靠度的时变性,能够很好地反映渡槽耐久性随时间的动态变化。
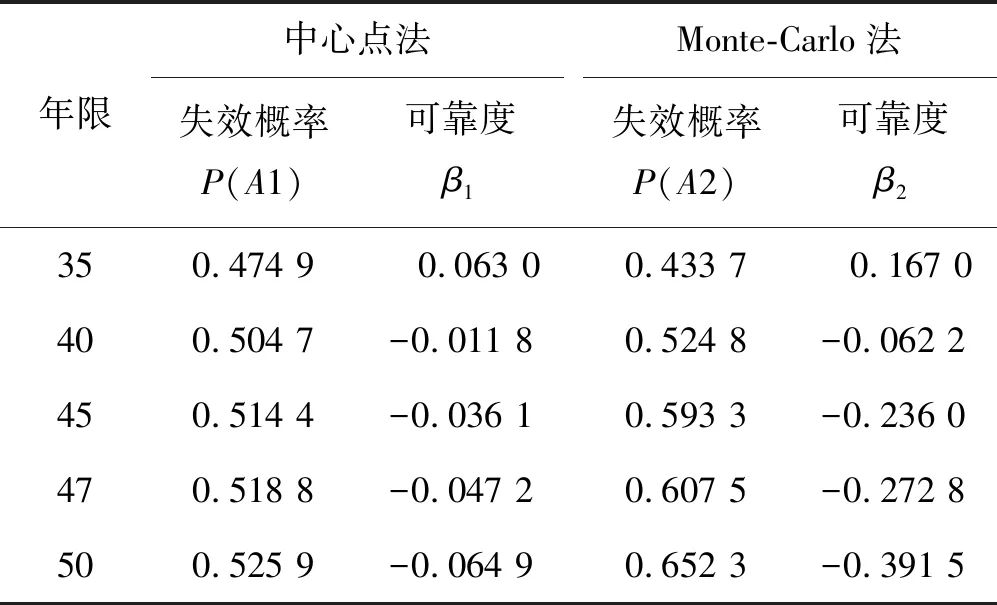
表2 渡槽失效概率与可靠度计算结果
将中心点法与Monte-Carlo法用于计算失效概率和可靠度,结果存在一定差异,这是因为两者的计算精度不同。采用中心点法与Monte-Carlo法对钢筋混凝土渡槽因钢筋锈蚀而失效进行模拟,可判断渡槽结构钢筋锈蚀的破坏程度,对实际工程具有一定的参考价值。
4 结语
(1) 针对在役渡槽钢筋锈蚀问题,基于钢筋锈蚀理论,采用中心点法与Monte-Carlo法建立了渡槽耐久性的时变可靠度预测模型,并对既有渡槽结构进行了相应的计算与分析。
(2) 中心点法与Monte-Carlo法对比表明,两者计算结果存在一定的差异。由于Monte-Carlo法更加精确与方便,因此建议在实际工程中采用Monte-Carlo法进行相关计算。
——以东风渠天宫桥渡槽和黎家沟渡槽为例

