基于灰色GM(1,1)-Markov的全国火灾形势综合评价与预测

陶钇希

(中国人民警察大学，河北 廊坊 065000)

0 引言

火灾是严重威胁人类生存和发展的非常规突发性灾害事故之一，特别是在多起群死群伤突发灾害事故中，所占比例较大，具有时空跨度大、发生频率高、社会影响大等特点。据统计，2009—2018年，我国平均每年发生火灾约25.1万起，造成1 450人死亡、956人受伤、直接财产损失33.14亿元，与1999—2008年相比，火灾起数平均增加约3.9万起，直接财产损失平均增加约18.81亿元。因此，基于历年火灾统计数据，运用科学的分析预测模型，实现对火灾形势的综合评价与预测，对客观认识、系统分析火灾发生、发展规律，优化配置消防资源，加强火灾防范，降低火灾损失，具有一定的理论指导意义和现实应用价值。

目前，针对火灾事故预测的研究主要采用Markov预测、小波分析、Logistic预测、指数平滑法、灰色预测等[1-6]理论和模型。针对灰色GM(1,1)-Markov理论在预测领域的应用，陈宝平[7]利用灰色GM(1,1)-Markov预测理论，对内蒙古自治区2016—2020年的电力需求进行预测。张和平等[8]建立了改进的灰色Verhulst预测模型，采用马尔可夫对改进的灰色Verhulst模型预测结果进行修正。杜晓燕等[9]以2006—2014年我国发生的危化品事故起数为原始样本，建立了灰色GM(1,1)-Markov预测模型，并以2015年我国危化品事故实际发生起数对模型进行了验证。杨琦等[10]运用多种方法对西安市2010—2011年城市公交客运量进行预测，结果发现灰色GM(1,1)-Markov预测模型的精度优于指数平滑法、模糊线性回归、灰色预测。

应当说，针对火灾事故预测的相关研究已经取得了一系列成果，但仍存在不足。首先，对象和指标的选取通常是特定的城市或火灾类型，缺乏对全国火灾事故的综合评价与预测；其次，选用的模型预测精度和准确度不高，对火灾形势的评价和预测不够准确。因此，本文将灰色GM(1,1)模型与Markov理论相结合，建立灰色GM(1,1)-Markov预测模型，并以我国2013—2018年的火灾起数、死亡人数、受伤人数、直接财产损失4项火灾评价指标为例，进行实例仿真计算和模型精度检验，并对2019年我国4项火灾评价指标进行预测，以期实现新时期我国火灾形势的综合评价与预测。

1 灰色GM(1,1)-Markov预测模型构建

1.1 灰色GM(1,1)模型

建立灰色GM(1,1)模型相应的微分方程为：

(1)

(2)

可解得灰色GM(1,1)方程的解，见式(3)。

(3)

将式(3)做一次累减即可得x(0)(t+1)序列的估计值：

(4)

1.2 灰色GM(1,1)-Markov预测模型

1.2.1 状态划分

1.2.2 状态转移概率矩阵构建

状态转移概率为：

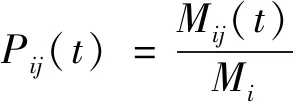
(5)

(6)

1.2.3 修正预测值

根据Markov状态转移概率矩阵，确定系统预测状态的转向，选取灰色GM(1,1)模型的相对误差值所在区间[Ri1,Ri2]的中值为修正值，修正灰色GM(1,1)-Markov预测值，计算见式(7)。

1.3 灰色GM(1,1)-Markov预测模型精度检验

本文选取平均相对误差λ、均方差比值σ和小概率误差P三种精度检验方法综合检验灰色GM(1,1)-Markov预测模型，精度检验等级标准详见表1。

平均相对误差λ为：

(8)

均方差比值σ为：

(9)

小概率误差P为：

(10)

表1 模型精度检验等级标准

2 实例计算

2.1 数据来源

本文选取火灾起数、死亡人数、受伤人数和直接财产损失4项指标来综合评价与预测我国火灾形势，使用数据来源于《中国消防年鉴》[11]及应急管理部消防救援局网站，详见表2。

表2 2013—2018全国火灾事故情况

2.2 灰色GM(1,1)预测

根据灰色GM(1,1)模型步骤及计算公式，可计算基于灰色GM(1,1)模型的全国火灾形势预测结果，详见表3。

2.3 灰色GM(1,1)-Markov预测

2.3.1 状态划分

为使各区间满足状态变化的客观规律，基于Markov理论，对相对误差值进行状态区间划分，详见表4。

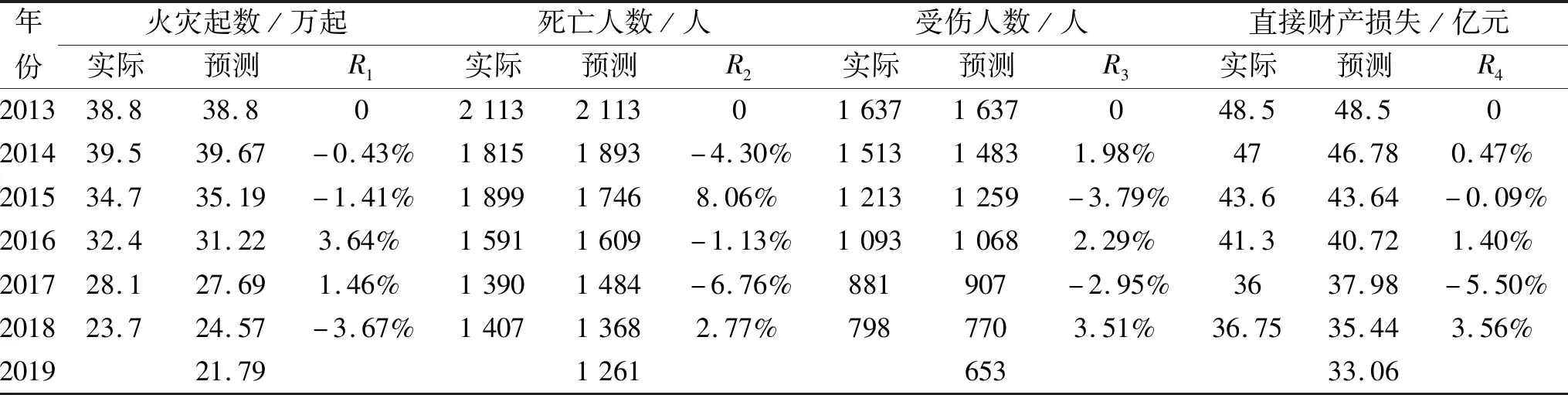
表3 基于灰色GM(1,1)模型的2013—2019年全国火灾形势预测结果

表4 状态划分标准

2.3.2 状态转移概率矩阵构建——以直接财产损失为例

根据状态划分区间和式(5)、式(6)，可得到各步状态的转移概率矩阵。

2.3.3 数量预测及修正——以直接财产损失为例

选取距离2019年最近的3个年份，根据距离2019年的远近，转移步数分别取1,2,3。在转移步数对应的转移状态概率矩阵中，选取初始状态所对应的行向量，组成新的状态概率转移矩阵，计算列向量之和，最大的即为2019年直接财产损失的预测转向状态。通过式(4)计算可知，2019年我国直接财产损失的灰色GM(1,1)预测结果为33.06亿元。由表5可知，2019年直接财产损失的预测转向状态为状态1，对应区间为(-6%,-2.7%]。因此，基于Markov理论将直接财产损失修正为31.63亿元。根据表2的4项火灾指标统计数据和相关计算步骤、公式，可得基于灰色GM(1,1)-Markov预测模型的2019年全国火灾形势预测值，其中火灾起数为21.79万起，死亡人数为1 240人，受伤人数为636人，直接财产损失预测为31.63亿元，详见表6。

表6 基于灰色GM(1,1)-Markov预测模型的2013—2019年全国火灾形势预测结果

2.4 预测模型预测数值对比及精度检验

图1～图4为4项火灾指标的两种模型与原始数据序列对比情况。从图可以看出，与灰色GM(1,1)模型相比，灰色GM(1,1)-Markov模型的拟合曲线较为平稳，4项火灾评价指标与实际值的吻合程度较高，能够较好地反映数据之间联系及波动。从表7可以看出，灰色GM(1,1)-Markov预测模型的平均相对误差λ、均方差比值σ和小误差概率P三项指标的精度等级与灰色GM(1,1)模型基本一致。但是，针对具体预测数据的相对误差和精度检验情况来看，灰色GM(1,1)-Markov预测模型明显优于灰色GM(1,1)模型。其中，基于灰色GM(1,1)-Markov预测模型的火灾起数、死亡人数、受伤人数和直接财产损失的平均预测精度分别达到98.902 %、98.306%、99.408%和98.890%，详见表3、表6。综合来看，灰色GM(1,1)-Markov预测模型适合我国火灾形势的综合评价与预测，预测结果精度较高。

3 结论

3.1 本文将灰色GM(1,1)模型与Markov理论相结合，一方面发挥灰色GM(1,1)模型所需样本数量低、中短期预测精度高的优点，另一方面发挥Markov理论处理波动性大的非平稳随机序列的优点，为我国火灾事故评价与预测提供参考与借鉴。

表7 两种模型预测精度对比

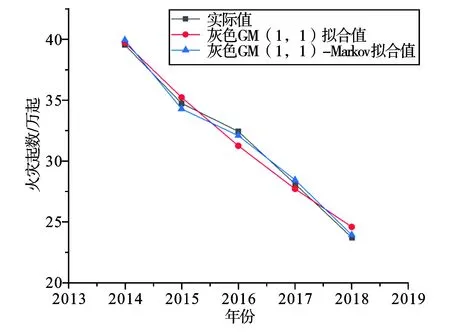
图1 火灾起数的对比情况

图2 死亡人数的对比情况

图3 受伤人数的对比情况

3.2 灰色GM(1,1)-Markov预测模型对火灾起数、死亡人数、受伤人数和直接财产损失4项指标预测精度较高，分别为98.902%、98.306%、99.408%和98.890%，适合于我国火灾形势的综合评价与预测。同时，对2019年全国火灾形势进行了预测，其中，火灾起数预测为21.79万起，死亡人数预测为1 240人，受伤人数预测为636人，直接财产损失预测为31.63亿元。

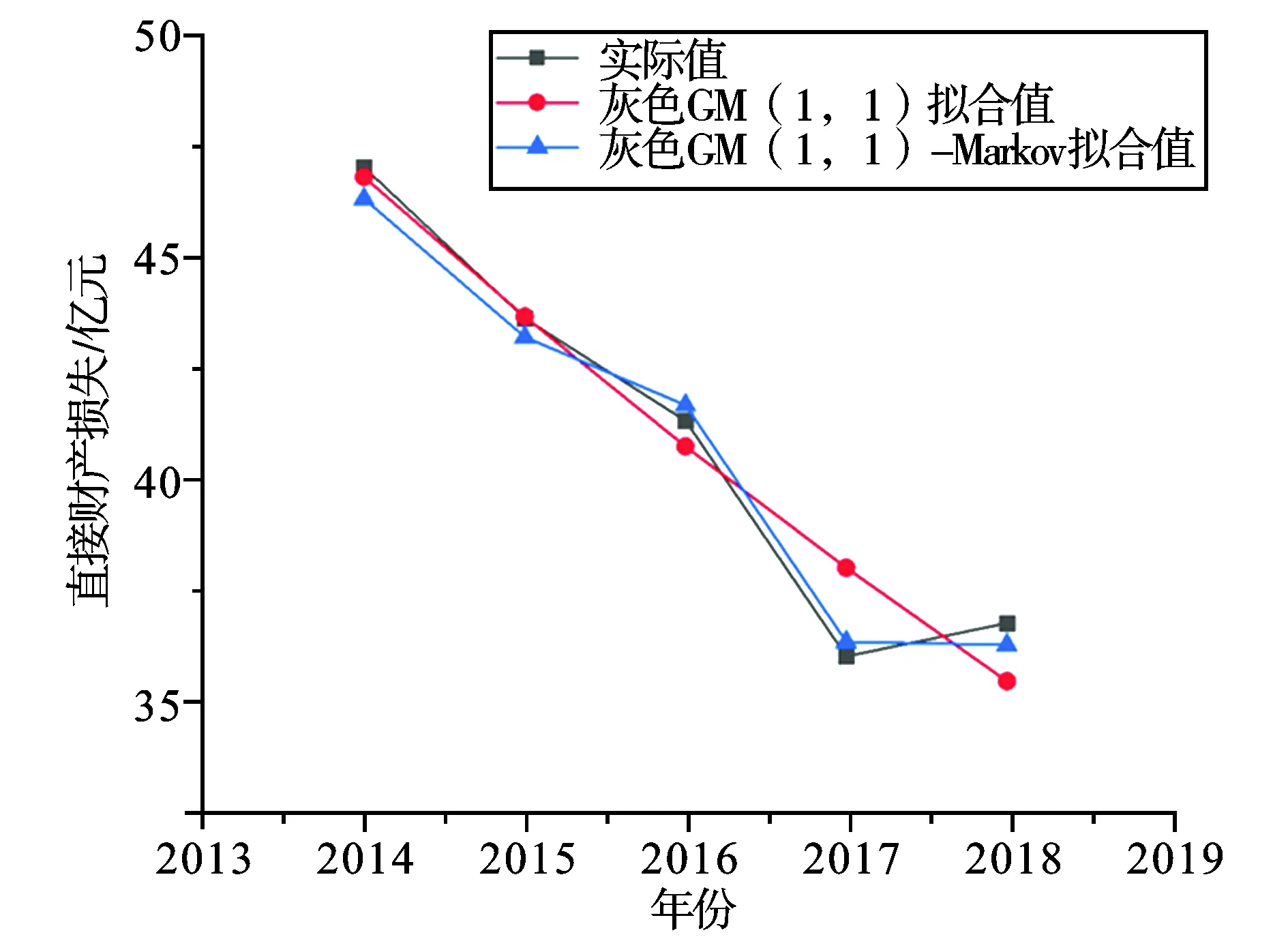
图4 直接财产损失的对比情况

3.3 火灾形势的综合评价与预测依赖于火灾统计数据的规范性、全面性、准确性和真实性。与美国等西方发达国家相比，我国的火灾事故信息化建设工作还有一定的差距，下一步应当建立完善的火灾信息统计标准和机制，加强对火灾信息的收集，才能更加全面系统地掌握、分析、预测我国的火灾形势，为今后消防工作的针对性开展提供理论支持。