钢轨波磨对车辆-轨道动态响应的影响

周昌盛，周华龙，王小韬，杨文茂，金忠凯

（中铁二院工程集团有限责任公司 地下铁道设计研究院，四川 成都 610031）

0 引言

随着现代城市规模的日益扩大，轨道交通作为一种新型的交通工具，以其运量大、速度快、安全可靠等特点，成为解决城市交通问题的重要手段[1]。然而随着城市轨道交通快速发展，轮轨伤损现象越加明显，其中较为普遍的问题为轮轨异常磨耗，包括钢轨波浪形磨损（简称钢轨波磨）、车轮多边形磨耗、钢轨侧磨、轮轨擦伤、车轮凹陷和沟槽形磨损等[2]。钢轨波磨不仅会直接引起车辆、轨道结构振动，增加工务维护费用、造成环境噪声污染，而且限制了车速进一步提高，并给行车安全带来隐患[3]。

随着行车速度提高、车流密度加大以及新型车辆和轨道结构的推广，钢轨波磨逐渐变得复杂。从20世纪70年代开始，各国科研人员更加注重这一问题。李伟等[4]采用钢轨波磨测量仪测量了钢轨波磨特征，采用加速度和位移传感器测量了钢轨打磨前后车辆和轨道零部件的振动加速度，分析了钢轨波磨对车辆和轨道零部件振动的影响。钟硕乔等[5]基于地铁车辆―轨道耦合动力学模型分析了科隆蛋扣件轨道的钢轨波磨对车辆动力学性能的影响，结果表明波磨主要影响了车辆系统的垂向振动特性。Ekberg等[6]结合高频车辆轨道动态模型和滚动接触疲劳模型分析了短波钢轨波磨对车轮疲劳的影响，考虑了不同运营条件下的波磨影响。

目前，我国城轨交通针对钢轨波磨的评价依据参照《铁路线路维修规则》，评价指标仅包含波深参量，而未考虑波长对轮轨激振的敏感性。且相比高速铁路而言，城轨具有线路曲线多、曲线半径小、行车密度高、车辆类型单一、车辆频繁加减速等特点，轮轨关系与高速铁路相比存在差异，直接采用高速铁路养护标准不一定合适，应针对城轨交通特点进行理论分析，制定适用于城轨的养护标准[7-9]。

鉴于上述现状，基于车辆-轨道垂向耦合动力学数值分析模型[10]，分析波磨波长、波深、行车速度对轮轨相互作用和车辆运行稳定性的影响，并以轮重减载率限值标准为判定依据，计算分析不同波长情况下波磨波深的建议控制值。

1 轮轨系统动力学模型

1.1 模型简介

车辆采用全车模型，考虑车体与转向架的沉浮与点头运动，车体与转向架之间由二系弹簧和阻尼器连接，转向架与轮对之间由一系弹簧和阻尼器连接[11-13]；由于无砟轨道中大部分弹性由扣件系统提供，且此处主要研究扣件刚度变化对轮轨系统的影响，因此轨道系统采用单层离散点支承模型，利用有限元法对其进行离散（见图1）。

1.2 系统垂向振动方程组建立及求解

哈密尔顿原理是分析力学中的一个基本变分原理，它提供了一条从一切可能发生的（约束所许可的）运动中判断真正的（实际发生的）运动的准则，是建立多自由度大型复杂结构系统动力学方程的最有效的基本原理和方法之一[14]。

根据系统的动力平衡原理，可以证明对于任何振动或运动系统，哈密尔顿原理可表达为：

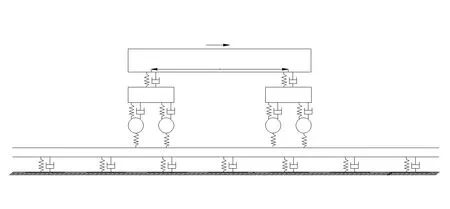
图1 全车-单层弹性点支承轨道平面模型

式中：δ为变分或虚位移符号；t1、t2为积分的起始和终止时间；T为系统总动能；U为系统总势能；δW为系统内保守力和非保守力所做的虚功总和。

基于哈密尔顿原理，根据系统的总动能、总势能及相应的虚功，结合计算机中的对号入座法则，可以很方便地建立车辆-轨道系统振动方程组：

式中：[M]、[C]和[K]分别为此系统质量、阻尼和刚度矩阵；、、{z}和{P}分别为此系统的加速度、速度、位移和载荷列阵。

模型建立之后，首先采用Wilson-θ法起步运算，然后再采用Park法求解振动方程组，其中Δt=1 ms，θ=1.4。

1.3 计算参数选取

计算过程中，车辆采用轴重16 t的地铁A型车，轨道结构参数见表1。

2 计算结果分析

2.1 对轮轨相互作用的影响

在车辆-轨道耦合系统动力学分析中，钢轨波磨属于轮轨接触界面几何不平顺激励形式[15-16]。钢轨波磨激励对轮轨相互作用的影响表现为轮轨接触载荷的波动。轮轨接触载荷波动对车辆运行的影响主要表现为：轮轨接触载荷最大值决定轮轨系统关键部件的受力水平，接触载荷越大，相关部件的受力水平越高，越容易出现病害[17-18]。因此，应严格控制轮轨接触载荷最大值。

计算波磨波深、波长以及行车速度对轮轨作用力的影响，不同参数对轮轨作用力的影响见图2。

从图2（a）可以看出，轮轨作用力随波深的增加而呈线性增长，当波深从0.05 mm增大到0.50 mm时，轮轨作用力由107.60 kN增大到371.50 kN，增大245%。当波磨波深为0.10 mm时，轮重减载率就已超出GB 5599规定的0.65安全限值。

表1 轨道结构参数

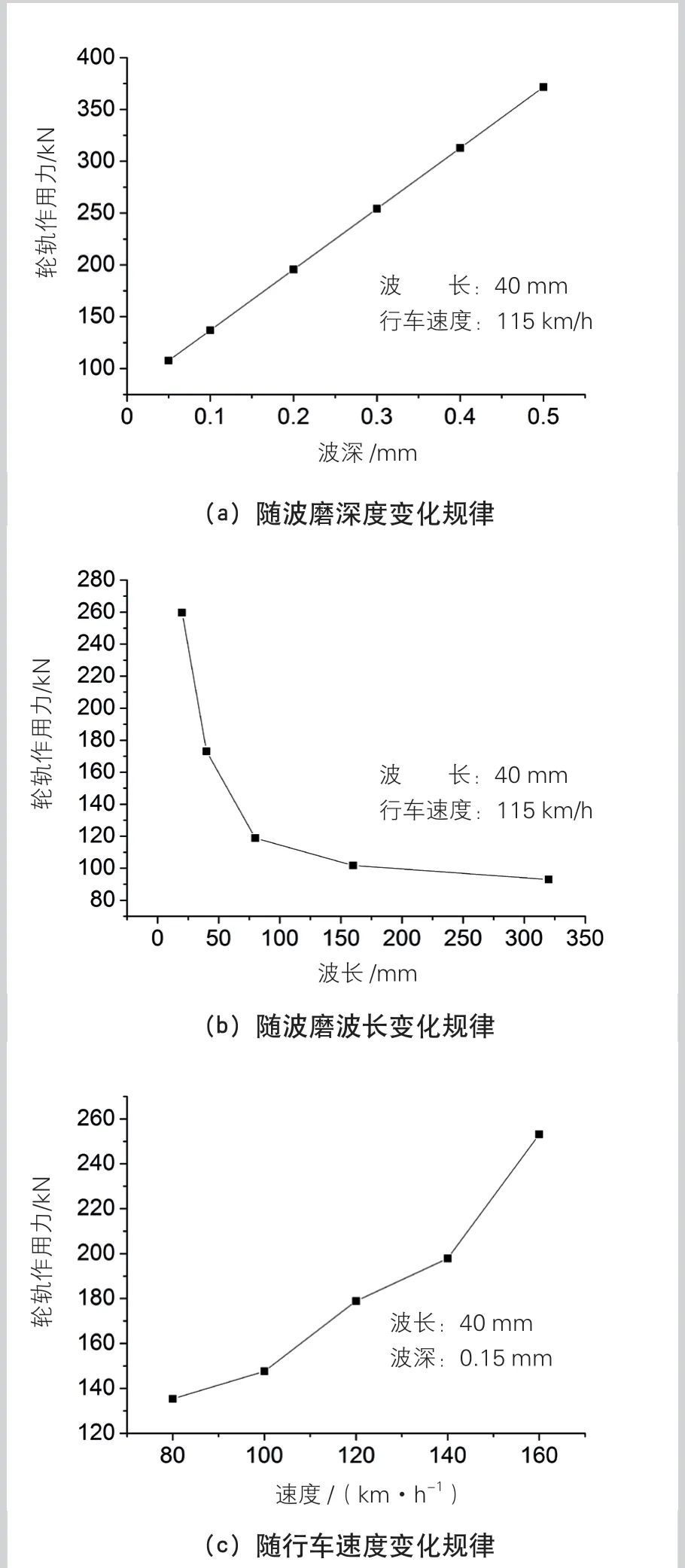
图2 不同参数对轮轨作用力的影响

从图2（b）可以看出，轮轨作用力随波长的增加而减小，当波长从20 mm增大到320 mm时，轮轨作用力由259.74 kN减小到92.98 kN，减小179%。当波长小于80 mm时，轮重减载率已超出GB 5599规定的0.65安全限值。

从图2（c）可以看出，轮轨作用力随速度的增加而增长，当速度从80 km/h增大到160 km/h时，轮轨作用力由135.35 kN增大到253.12 kN，增大87%。且轮轨系统振动响应对短波波磨敏感性强，在速度为80 km/h时轮重减载率就已超出GB 5599规定的0.65安全限值。

可见，地铁与高速铁路产生的病害情况存在差异，直接套用高速铁路养护标准不一定合适，应针对城轨交通特点进行理论分析，制定真正适用的打磨标准。

2.2 对车辆运行稳定性的影响

振动加速度是影响车辆运行稳定性的重要因素。轮轨接触载荷作为车辆-轨道系统的激励源，直接激励轮对和钢轨，使其获得振动能量，做受迫振动[19]。

波磨波深、波长以及行车速度对车辆运行稳定性的影响见图3。可以看出，车体加速度绝对值较小，比轮对加速度小4个数量级。

从图3（a）和（b）可以看出，车体加速度和轮对加速度随波深的增加呈线性增长。当波深从0.05 mm增大到0.50 mm时，车体加速度由0.0078 m/s2增大到0.0756 m/s2，增大869%；轮对加速度由57.15 m/s2增大到567.52 m/s2，增大893%。

从图3（c）和（d）可以看出，车体加速度随波长的增加而增长，且增加速率有逐渐增大的趋势；轮对加速度随波长的增加而减小，且减小速率有逐渐减小的趋势。当波长从20 mm增大到320 mm时，车体加速度由0.021 m/s2增大到0.047 m/s2，增大124%；轮对加速度由267.58 m/s2减小到20.51 m/s2，减小1 204%。

从图3（e）和（f）可以看出，行车速度对车体加速度影响较小；对轮对加速度影响显著，且随行车速度的增大而显著增大。当速度从80 km/h增大到160 k m/h时，轮对加速度由1 1 8.9 6 m/s2增加到275.97 m/s2，增大132%。

可见，由于车体加速度绝对值较小，因此地铁钢轨波磨和行车速度对车体振动响应的影响可以忽略。然而，波磨和行车速度对轮对振动响应影响十分明显，整体表现为波磨深度和行车速度越大，轮对振动加速度越大。

2.3 对车辆运行安全性的影响

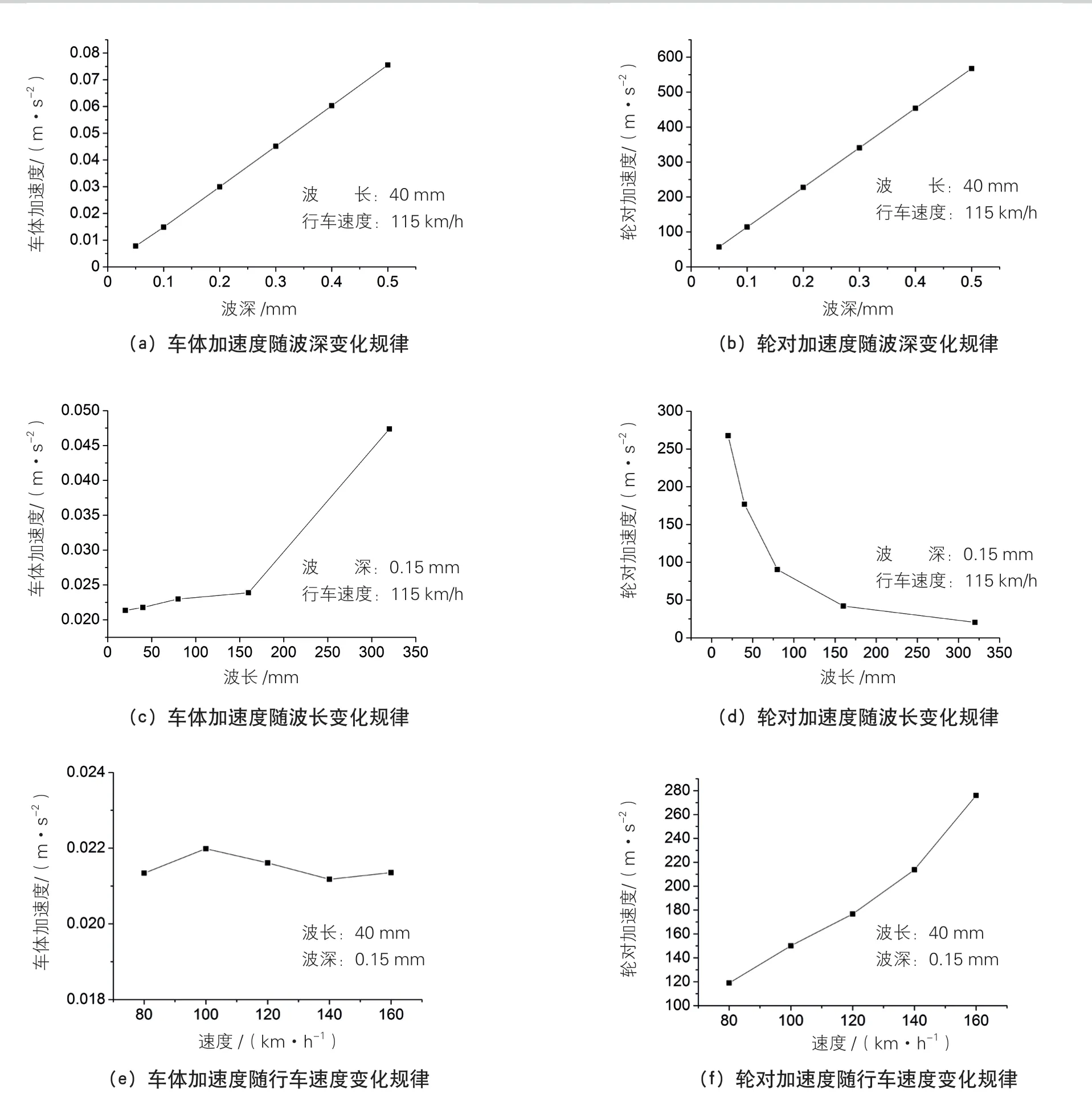
图3 不同参数对车辆运行稳定性的影响

轨道车辆运行时会受到各种不利因素的影响，最不利因素的组合影响下会产生轮轨分离甚至脱轨现象，这对车辆及旅客的安全性极为不利[20]。因此研究车辆运行安全性极为重要。脱轨系数是评价车辆运行安全性的重要指标[21]，计算得到的波深、波长和行车速度对车辆运行安全性的影响见图4。

由图4（a）可以看出，脱轨系数随波深的增大而增大。当波深从0.05 mm 增大到0.50 mm时，脱轨系数由0.21增大到0.58，增大176.19%，从脱轨系数变化率来看，波深对于行车安全性影响较大，但仍满足GB 5599规定的1.1安全限值。

由图4（b）可以看出，脱轨系数随波长的增大而减小，但波长超过70 mm以后脱轨系数对波长变化敏感度下降。当波长从20 mm增大到320 mm，脱轨系数由0.350降低到0.261，下降了25.4%，满足GB 5599规定的1.1安全限值。

由图4（c）可见看出，脱轨系数随行车速度的增大而增大，车速小于120 km/h时增大速率较缓和，当车速高于120 km/h时，脱轨系数随车速的增大而增大的速率变大。当车速从80 km/h增大到160 km/h时，脱轨系数由0.22增大到0.55，增大150%，满足GB 5599规定的1.1安全限值。

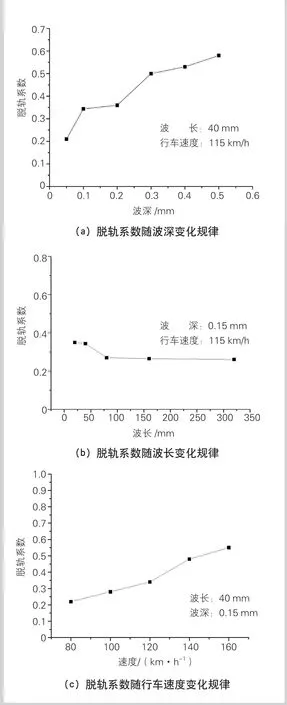
图4 不同参数对车辆运行安全性的影响

可见，脱轨系数随钢轨波深和行车速度的增大而增大，随钢轨波长的增大而减小，且波长超过70 mm后，脱轨系数对波长变化的敏感度降低。

3 波深控制建议值分析

首先对不同钢轨波磨状态下轮轨作用力进行计算分析（见图5），可以看出，钢轨波磨波长越长，轮轨作用力对波深的敏感性越弱。因此，对于不同波长钢轨波磨，其波深限值应不同，对于短波波磨应更加严格控制其波深。

轮重减载率变化曲线见图6，可以看出，轮重减载率随波深及波长的增加而增大。以0.65的轮重减载率限值标准为判断依据，可得出不同波长下波深的控制建议值（见表2）。

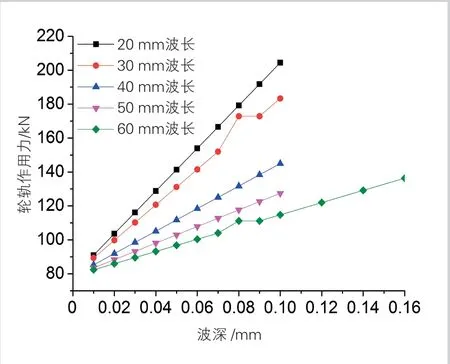
图5 轮轨作用力变化曲线

图6 轮重减载率变化曲线

表2 不同波长下波深的控制建议值 mm

4 结论

（1）钢轨波磨越严重，轮轨相互作用越激烈；轮轨作用力随波深和行车速度的增加呈线性增长，随波磨波长的增加而减小。

（2）不同波深、波长以及行车速度对轮对和车体的振动加速度影响依次减小，车体加速度比轮对加速度小4个数量级。钢轨波磨和行车速度对车体振动响应的影响可以忽略，而波磨和行车速度对轮对振动响应影响十分明显，整体表现为波深和行车速度越大轮对振动加速度越大，波长越长轮对振动加速度越小。

（3）通过车辆-轨道垂向耦合动力学数值分析模型，分别计算不同波长、波深时轮轨作用力，并以0.65的轮重减载率限值标准为判断依据，分析给出了20～60 mm波长范围内波深控制建议值，建议波长为20、30、40、50、60 mm短波钢轨波磨波深分别达到0.05、0.04、0.06、0.06、0.09 mm时进行打磨处理。