涡轮盘应力集中系数估算方法

摘  要：以Ansys Workbench计算的涡轮盘盘心应力集中系数结果为基础，用Matlab编程偏最小二乘法程序，计算得出涡轮盘尺寸参数和盘心应力集中系数的拟合关系式，将拟合方程的计算结果和二维有限元应力计算结果进行对比，发现两者计算结果具有相似的变化趋势，误差平方和约为0.08。表明偏最小二乘法对涡轮盘盘心应力集中系数的拟合计算有一定可行性，为涡轮盘结构正向设计提供了工具支撑。

关键词：航空发动机;方案设计;涡轮盘;盘心应力集中系数

中图分类号：V23   文献标识码：A  文章编号：1671-2064（2019）16-0000-00

设计航空发动机涡轮盘时，需要根据涡轮盘的工作条件和几何形状，计算涡轮盘的应力分布状态，确保应力水平满足安全储备系数要求。

航空发动机的涡轮盘的盘心存在应力集中，通常也是涡轮盘周向应力最大的位置。该处是涡轮盘的基本构型，决定了涡轮盘在转子组件上的装配关系。如果在方案设计阶段能够明确各个尺寸参数对涡轮盘盘心应力集中系数的影响，那么设计人员就能进行有效率的正向设计，从而缩短涡轮盘的研制周期。

应力集中系数是无量纲常数，通常只取决于构件的形状，因而又被称为“形状系数”，不同构件的应力集中系数通常通过有限元计算或试验测算得出。

航空发动机涡轮盘的几何参数较多，使用传统响应面计算方法难以拟合自变量较多的数据集。而建立通过试验测算得出的盘心应力集中系数的数据库的成本又过大。本文拟采用偏最小二乘法（Partial Least-Square method，PLS）对合理设计尺寸范围内的涡轮盘盘心应力集中系数进行分析拟合。该数学优化方法的特征为：（1）能够在自变量较多，样本较少的条件下回归建模;（2）能够在自变量严重耦合的条件下回归建摸;（3）最终模型中包含所有自变量;（4）回归模型易于辨识系统的信息和噪声。

本文通过Ansys Workbench软件对涡轮盘二维模型进行计算分析，得出应力集中系数对应涡轮盘几何参数的数据图表。然后通过Matlab软件编程，使用偏最小二乘法程序对应力集中系数和涡轮盘几何参数的数据集进行拟合，得到涡轮盘盘心的应力集中系数近似解计算公式。从而达成初步预测中小型航空发动机涡轮盘方案设计阶段盘心的应力集中系数大小的目的。

1涡轮盘数学建模

在分析涡轮盘应力大小时，可以简化轮廓，去除涡轮盘幅板上的鼓筒，以及盘彀上的端齿。以一侧的轮廓面为基础，重新构建涡轮盘。

涡轮盘二维简化模型如图1所示，可以用轴向和径向的变量，x₁、x₂、x₃、x₄、x₅、x₆、x₇、x₈、R₀、R₁、R₂、R₃、R_b这13个参数表示涡轮盘的轮廓尺寸。

由于应力集中系数对于形状固定的构件是无量纲常数，满足相似设计原则。可以涡轮盘榫槽底直径为设计基准进行分析，除h_b之外所有参数都可以与h_b相除，等比计算盘心应力集中系数。

在Ansys Workbench软件建模中，将R_b设定为常量（设为无量纲常数1，运算最为方便），x₁、x₂、x₃、x₄、x₅、x₆、x₇、x₈、R₀、R₁、R₂、R₃这12个变量和R_b的比值为自变量。

使用Ansys Workbench的参数关系运算分析工具，在一定范围内改变每个参数的取值，并批量计算这些自变量关联盘心应力集中系数K_t的数据集。

2 参数拟合方法

2.1线性化分析响应关系

应用偏最小二乘法前，首先需将12个尺寸自变量相对因变量，即应力集中系数的关系分别线性化。将其转化为以下形式：

式中： ～——12个尺寸参数对应应力集中系数独立的拟合函数;

～——對应以上12个拟合函数的参数;

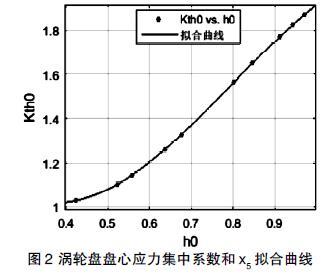
首先，分析和对应的函数关系，令除了以外所有的参数不变，在表1中的上、下限所示的区间内随机均布取值，以Ansys Workbench计算10组结果，其关系如图2所示。

拟合的方程舍去常数项的表达式为：

拟合后的曲线的残差平方和约为1，说明符合性非常好。

其他参数取值不同时，该关系式并不是唯一的，但由于在表1所示的自变量基础设定值变化的上、下限范围内，该函数的变化较小，仍有一定拟合参考性。

同理对、对应的函数关系进行分析。这两个自变量的拟合方程舍去常数项的表达式为：

;

;

其中的残差平方和约为1，的残差平方和约为0.9944，拟合性较好。

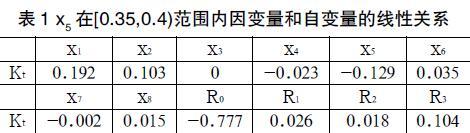
从以上自变量和因变量的关系对比可以看出，自变量在一定取值区间内，可以用二次函数拟合因变量。本文为相关性较强的自变量的取值区间进行分段，以[0.3，0.35），[0.35，0.4），[0.4，0.45），[0.45，0.5），[0.5，0.55），[0.55，0.6），[0.6，0.65），[0.65，0.7]为设计常用取值区间，每个区间运算300个有限元算例，统计盘心应力集中系数计算结果和参数关系。如表1所示。

根据以上计算结果，为简化运算，仅计算关系因子的绝对值大于0.05的因变量和自变量之间的关系。即可拟合该条件下的应力集中系数。

2.2偏最小二乘法分析方法

以为自变量向量，以为因变量向量;以为自变量矩阵，以为因变量矩阵。共统计数据组。表达式如下：

（1）计算矩阵最大特征值对应的特征向量，求成分，其算其得分向量，残差矩阵为：

式中， 。

（2）计算矩阵最大特征值对应的特征向量，求成分，其算其得分向量，同理计算残差矩阵。

……

（r）计算矩阵最大特征值对应的特征向量，求成分，其算其得分向量。

原有自变量和因变量数据则可以表达为：

将代入，则可得到最小二乘回归方程：

由于残差矩陣的秩必然小于原有数据矩阵，故小于等于自变量个数。但通常来说，就像主成分分析一样，只用选择前个成分以内的，就能得到预测性较好的结果。故使用交叉有效性检验方法， 确定的实际取值。

拟合所有样本点时，令拟合结果为预估值矩阵。令预测值的误差平方和为，预测误差平方和为。通常，总有大于，小于，当比值

时，可以认为拟合结果满足使用需求。

本文通过Matlab软件对以上计算过程编程，以为例，拟合方程如下所示。

3 算例分析

将拟合的300组数据进行综合计算分析，求得拟合方程的计算结果和有限元计算结果的误差平方和为0.08。拟合方程的计算结果和有限元计算结果对比如图3所示。

样本按有限元计算值的大小降序排列。根据以上的计算和对比可知，拟合计算结果虽然产生振荡，但变化趋势和有限元计算结果仍然吻合。最大的偏差不大于0.08。

4 结论和展望

（1）采用偏最小二乘法拟合航空发动机涡轮盘心应力集中系数，得到的多维响应面拟合方程有较好的精确性，能够满足方案设计需求;

（2）根据2.1节计算结果，盘心厚度对应力集中系数影响很大，且与应力集中系数呈现明显的正相关关系。和应力集中系数负相关，随它增长，应力集中系数减小;

（3）Matlab编写的偏最小二乘法计算程序可以对不同的有限元计算数据集进行统计拟合，当涡轮盘变形程度大于本文拟合计算的尺寸参数上、下限时，可以通过扩充计算数据、分段计算应力集中系数计算结果的办法，改进拟合方程系数，满足实际设计需求。有良好的可扩性和可维护性。

参考文献

[1] 吕文林主编.航空发动机强度计算[M].国防工业出版社，1988，12.

[2] 《航空发动机设计手册》总编委会主编.航空发动机设计手册[M].航空工业出版社，2001，9.

[3] 航空工业部科学技术委员会主编.应力集中系数手册[M].高等教育出版社，1990，6.

收稿日期：2019-07-10

作者简介：张若昀（1985—），男，湖北武汉人，硕士，涡轮结构主管设计师，工程师，研究方向：航空发动机涡轮部件结构课题。

An Estimation Method for Stress Concentration Factor at Turbine Disk

ZHANG Ruo-yun

（Aecc Hunan Aviation Powerplant Research Institute，Zhuzhou Hunan  412002）

Abstract：On the basis of concentration factor for fatigue analysis of turbine disc center calculated by Ansys Workbench， a fitting equation of relationship between turbine discs size and turbine disc centers concentration factor was presented， by using the PLS method programmed with Matlab. The results calculated by fitting equation and finite element method were compared， the trends of the results were approximately in agreement with each other， and error sum of squares was 0.08. This comparison proved PLS methods application value for the calculating of turbine disc centers concentration factor， which can provide reference for the forward design of the aero engine.

Key words：aero engine;scheme;turbine disc;stress concentration factor of turbine disc center