多基线InSAR仿真干涉图相位解缠技术研究

唐洪城

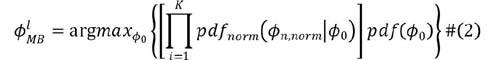
【摘 要】多基线干涉SAR技术结合了长短基线的优点，从而可获得较高的高程测量精度。本文基于多基线最大似然估计法（MLE）对仿真干涉图进行相位解缠，并在此基础上加入低分辨率DEM作为先验信息，降低噪声的影响。实验表明：MLE方法能大致反演出地形相对趋势，但易受到噪声影响;而基于低分辨率DEM的最大后验估计相位解缠算法能够很好地降低噪声影响，从而获得较高精度的DEM。

【关键词】多基线InSAR;数字高程模型;最大似然估计;最大后验估计

中图分类号： TN957.52文献标识码： A文章编号： 2095-2457（2019）32-0007-002

DOI：10.19694/j.cnki.issn2095-2457.2019.32.002

Research on the Technology of Phase Unwrapping of Simulated Multi-baseline InSAR Interferograms

TANG Hong-cheng

（College of surveying and Geo-informatics， Tongji University， Shanghai 200092， China）

【Abstract】Multi-baseline interferometric SAR technology combines the advantages of long and short baselines to obtain higher elevation measurement accuracy. In this paper， the phase unwrapping of the simulation interferogram is carried out based on the multi-baseline maximum likelihood estimation （MLE） method， and low-resolution DEM is added as prior information to reduce the impact of noise. The experiment shows that MLE method can roughly reverse the relative trend of the terrain， but it is easy to be affected by noise. However， the maximum posteriori estimation phase unwrapping algorithm based on low-resolution DEM can effectively reduce the noise effect， so as to obtain a DEM with relatively high accuracy.

【Key words】MB-InSAR; DEM; Maximum Likelihood Estimation; Maximum a Posteriori Estimation

0 引言

在多基线InSAR测量技术中，国内外对于相位解缠的研究较多。Xu[1]等提出可将中国余数定理、平面投影和线性组合等思想应用到多幅干涉图的相位解缠中;Kim[2]等研究了利用Kalman滤波技术进行多基线InSAR相位解缠的方法;Ghiglia[3]等提出了完全基于传统最小二乘（Least Square）的相位解缠方法，以及基于最大似然估計（MLE）的相位解缠方法。前者先对多基线干涉相位按基线和信噪比进行加权平均，然后再直接利用最小二乘方法进行相位解缠;后者基于干涉相位的概率似然密度函数进行处理。上述两种方法均容易受到相位噪声的影像，所以本文将低分辨率DEM作为先验信息[4]从而约束最大似然估计方法中周期模糊问题，并成功得到精确的高程结果。

1 多基线InSAR最大似然相位解缠及其改进方法

基于多基线最大似然相位解缠方法利用了干涉图干涉相位的概率分布，其算法的核心原理在于不同的干涉相位之间相互独立，对于单基线情况而言，干涉相位存在如下的概率密度函数式[5]：

式中：ξn为各干涉图垂直基线长度比，|？酌n|代表相干系数值的绝对值，φn为真实干涉相位，φ0为真实相位的估计值，从上式看出，由于概率密度函数对相位差作了余弦运算，所以其周期为2π。当解缠相位φn是真实相位φ0的准确估计或相差2π的整数倍时，概率密度函数取得最大值。故可以通过检测概率密度函数的最大值来进行相位估计，但由于该函数具有周期性，有多个极值，所以对单基线情况下所得的解不唯一[6]。

在有噪声存在的情况下，多基线最大似然相位解缠结果受噪声影响往往出现离散分布的尖锐毛刺。为了约束噪声影响，文献[4]采用低分辨率DEM作为先验条件的最大后验估计相位解缠方法。当获取一幅低分辨率DEM后，首先结合雷达系统参数信息将低分辨率DEM高程值转化为相位，则多基线InSAR的相位最大后验估计为：

式中：pdf（φ0）是从低分辨率DEM中获取的相位先验分布。

2 多基线InSAR相位解缠实验与效果评价

为了验证本文方法的性能，本节基于已有空间分辨率为20m的贵州六盘水地区局部DEM仿真了三幅垂直基线长度分别为178m、83m以及47m的SAR干涉图，为了对比各算法的抗噪能力，我们同时在干涉图中附加了标准差为0.2 rad的加性高斯噪声，如图1所示。仿真雷达波长为0.031m，入射角为38°，卫星轨道高度为600km，干涉图所对应的相干系数差异仅取决于垂直基线的长度，且整张干涉图相干系数值设置相等，分别为：0.31、0.47、0.50。

在数据处理时，分别采用多基线最大似然相位解缠以及基于低分辨率DEM的最大后验估计相位解缠算法对仿真干涉图进行解缠处理，本文所用低分辨率DEM是将仿真所采用的DEM经过15*15窗口滑动平均后所得到，我们将其视为先验DEM，并将高程值其转化为相位值，用于在最大后验估计中计算相位的先验概率密度，得到解缠相位后，再结合已有参数，将相位转化为高程。

接着，我们采用原始DEM作为真实值，分别将低分辨率DEM、多基线最小二乘算法生成的DEM以及其改进算法生成的DEM分别与原始DEM进行作差，表1列出了各结果高程误差的统计值。

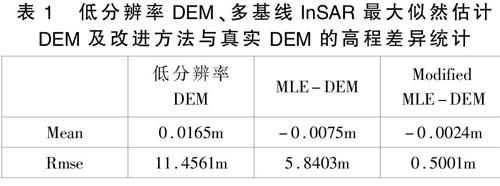
表1 低分辨率DEM、多基线InSAR最大似然估计DEM及改进方法与真实DEM的高程差异统计

从表1的高程差异统计结果可以看出，多基线最大似然估计DEM以及加入了低分辨DEM进行改进的最大似然估计生成的DEM的均方根误差分别为5.8403m、0.5001m，二者均比原先低分辨率的DEM精度即11.4561m要高。此外由于有先验DEM的约束，改进后的最大似然估计法受噪声影响较小，相位解缠精度由5.8403m提高到了0.5001m。

3 结论

本文针对干涉相位概率密度函数分布特性，基于已有地形仿真出多幅干涉SAR影像，并采用最大似然估计相位解缠法将三幅影像联立求解，从而恢复出缠绕相位的真实值，但是该方法往往受到干涉图噪声影响，使得解缠后相位图在噪声点处解缠错误。所以本文采用现有低分辨率DEM对每个像素高程进行约束，缩短模糊周期。通过仿真和分析可以看出，本文的方法均可以起到对现有低分辨率DEM进行更新的作用，同时，加入低分辨率DEM后的最大似然估计方法对噪声的影响具有一定的抵抗能力，有利于高精度DEM的生成。

【参考文献】

[1]X.Wei， E.C.Chang，L.K.Kwoh，et al. Phase-unwrapping of SAR Interferogram with Multi-frequency or Multi-baseline[C]. Geoscience and Remote Sensing Symposium Proceedings，Singapore，1994：730-732.

[2]M.G.Kim， H.D.Griffiths. Phase Unwrapping of Multibaseline Interferometry using Kalman Filtering[C].Seventh IEEE International Conference on Image Processing and Its Application， London， UK， 1999：813-817.

[3]D.C.Ghiglia， D.E.Wahl. Interferometric Synthetic Aperture Radar Terrain Elevation Mapping from Multiple Observations[C]. Digital Signal Processing Workshop， sixth IEEE， Albuquerque， NM， USA，1994： 33-36.

[4]蔣厚军.高分辨率星载InSAR技术在DEM生成及更新中的应用研究[D].武汉：武汉大学， 2012.

[5]Xu， Huaping， Li， Shuo，et al. Unwrapped Phase Estimation via Normalized Probability Density Function for Multibaseline InSAR[J].Digital Object Identifier，2019，07： 4979-4988.

[6]郭立文.多基线InSAR数据处理技术及应用研究[D].成都：电子科技大学， 2016.