受桩顶沉降量控制的嵌岩桩承载特性研究

温 树 鑫

(中国水电建设集团十五工程局有限公司，陕西 西安 710065)

桩基础的承载力比其他形式的基础高，但沉降量却更小，而且其适应性也很强，所以桩基础广泛应用于路桥工程中。对于平地桩基础的理论分析已基本趋于完善，但对于陡坡地段下的受荷桩，却需要具体问题具体分析，无法采用一个共同的理论或者通式去研究[1,2]。如张学明等通过建立神经网络模型，发现荷载与沉降之间的映射关系，从而使特殊点的位置更精确，得出的承载力也就越接近桩基的实际承载力[3]。

对于嵌岩桩而言，桩基的材料强度不足和桩端岩体破坏是控制桩基承载力的主要因素，目前的研究大多也是集中在分析影响嵌岩桩承载力发挥的因素[4]。如霍少磊，龚维明在考虑长径比对端阻的影响以及嵌岩比对端阻和侧阻的影响的基础之上，得出了较合理的桩基承载力计算的影响系数[5]，为嵌岩桩的承载力计算提供了参考。但是，对于处于岩质陡坡环境下的桩基，其岩土层的强度可能并不够高，无法有效限制桩基的沉降量。那么，上部结构就可能因为沉降量过大而无法继续工作甚至破坏。此时，就必须考虑桩顶沉降量对桩基承载特性的影响。

本文推导了按桩顶沉降控制的嵌岩桩的控制微分方程，并建立了桩侧岩土体处于弹性阶段时桩顶极限荷载的求解方法。最后以一具体工程的嵌岩桩作为研究对象，对该桩基按桩顶沉降量控制进行竖向承载力计算。

1 竖向位移的控制微分方程求解

假设桩侧阻力的分布[6]如下：

(1)

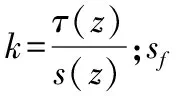
化取4 mm～6 mm；τr为残余侧阻力。

假设桩端阻力按照三折线函数分布：

(2)

其中，kb1,kb2分别为沉渣与岩土体的端阻传递系数；ξ0,ξf分别为桩端弹性压缩阶段的初始位移与结束点的位移；qpf为端阻极限值。

根据桩基的传递函数控制微分方程，即：

代入τ(z)的分布函数，有：

(3)

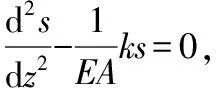
从数学上可知，双曲函数：

故，s(z)又可写成：

s(z)=(c1+c2)sinh(rz)+(c1-c2)cosh(rz)。

由于常数c1,c2可根据初始条件求得，故可将常数进行合并，即写成：

s(z)=c1sinh(rz)+c2cosh(rz)。

同理，可求得s≥sf时方程的解，直接化简并积分两次可得：

综上，按桩顶沉降控制的嵌岩桩的控制微分方程为：

(4)

2 按桩侧岩土体处于弹性阶段的桩顶极限荷载求解

假定桩顶的初始沉降量为s0，桩周岩土有n层，故其初始边界条件和连续性条件为：

由于桩侧土体处于弹性阶段，故第i层的沉降应采用s

si=c1isinh(riz)+c2icosh(riz)。

代入桩顶参数，即z=0时，有：

c21=s0；

则连续性条件为：

解线性方程组可得常系数c1i,c2i的值，从而解出各岩土层的竖向沉降表达式Si，并求得桩顶极限荷载N的表达式：

(5)

根据现场资料，查得桩基的刚度EA以及各项参数，即可求解出桩顶极限荷载的具体值。

3 案例分析

3.1 依托工程整体介绍

G4216线仁寿经沐川至屏山新市(含马边支线)段高速公路(以下简称仁沐新高速公路)马边支线段路线起于仁寿经沐川至屏山新市镇高速公路主线新凡乡附近，与主线沐川枢纽相接，止于马边县城北侧红牌坊大桥附近，全长43.847 km。其中桥梁1 332 m/3座，马边河1号大桥左线772 m，右线772 m；罗汉溪中桥左线40 m，右线40 m；马边河2号大桥左线525 m，右线514 m。本文取马边河2号桥沐川岸左线陡坡上的嵌岩桩作为研究对象，对该桩基按桩顶沉降量控制进行竖向承载力计算。

3.2 按桩顶沉降量控制的桩基竖向承载力计算

根据设计和施工等单位提供的资料可知：桩基的弹性模量E=30 GPa，桩长l=17 m，桩径为2 m。桩侧摩阻力的传递系数k=600 kPa/mm，在考虑沉渣的影响时，桩侧摩阻力到达极限值时桩端位移ξ0=s0=1 mm，桩端阻力的传递系数k1=80 kPa/mm,k2=800 kPa/mm，桩端阻力到达极限时桩端位移ξf=sf=1.8 mm。

代入公式有：r=0.2 m-1，β1=0.026 7 m-1，β2=0.266 7 m-1，λ=-1.26×10-5m，h2=0.998 7，c11=λ+h2s0=9.861×10-4m。

所以，按桩顶沉降量控制的嵌岩桩桩顶极限荷载为：

N=EArc11=18 587.758 kN。

选取安全系数[K]=2.0，则桩顶竖向荷载容许值为9 293.879 kN。

根据现场所提供的数据可知，纵坡向双桩式基础的桩顶荷载为16 000 kN，平分到两根基桩后为8 000 kN，小于计算出的荷载容许值，因此该桩基的竖向承载力是满足要求的。而且，桩侧摩阻力与桩端阻力未进入塑性阶段，所以该桩基的受力远低于其承载力。这在验证该公式可行性的情况下，又说明了该理论公式较保守，还可做进一步的简化考虑，从而可以节约工程造价。

4 结语

本文推导了按桩顶沉降控制的嵌岩桩的控制微分方程，并建立了桩侧岩土体处于弹性阶段时桩顶极限荷载的求解方法。最后以四川仁沐新高速公路马边河2号桥沐川岸左线陡坡上的嵌岩桩作为研究对象，对该桩基按桩顶沉降量控制进行竖向承载力计算。结果表明依托工程的桩基的竖向承载力是满足要求的。而且桩侧摩阻力与桩端阻力未进入塑性阶段，表明该桩基的受力远低于其承载力。研究结果不仅验证了理论公式的可行性，而且说明了该理论公式偏保守，有待进一步优化从而节约工程造价。