基于拓扑网格方法的多钝体流致振动分析
丁 林, 邹 瑞, 张 力, 邹群峰
(1. 重庆大学 低品位能源利用技术及系统教育部重点实验室,重庆 400044; 2.重庆大学 能源与动力工程学院,重庆 400044)
钝体是工程中一种常见的非流线型结构,在一定的流速下,流体绕流钝体后会在钝体两侧交替脱落旋涡。旋涡脱落会在结构表面形成周期性脉动力,当钝体固定方式为弹性支撑或允许发生形变时,脉动力将引起钝体振动,即流致振动[1]。在一切与流体有关的机械与工程中,流致振动都是一个涉及安全性的重大问题,在工程实践中受到广泛关注。多钝体流致振动是一个较为复杂的流固耦合过程,流场与多个运动结构的耦合计算还需进一步优化,这不仅有利于分析多钝体流致振动动力学响应的影响参数,而且可以更加深入地了解多钝体流致振动特性及旋涡演变过程,具有非常重要的理论研究意义与工程应用价值。
圆柱是一种常见的钝体结构,目前关于单圆柱绕流流致振动问题的研究已经取得了非常丰硕的成果[2-3],孙丽萍等[4]采用了改进的k-ε湍流模型,研究了加速度对涡激振动响应的影响,优化了数值模拟方法,实现对单圆柱双自由度涡激振动较精确的数值模拟;陈正寿等[5]试验发现,低质量比圆柱对应的锁振区范围要广于高质量比圆柱,低质量比圆柱横向振幅较大,涡激振动现象更为显著。相比单圆柱绕流流致振动,在实际工程中多圆柱绕流流致振动的情况更为普遍。双圆柱串行排列是最为简单的多钝体系统,固定双圆柱绕流的研究已经取得诸多成果[6-7],但是双圆柱流致振动的研究却有待深入,目前主要集中于最简单的尾流振动模型[8-9]。双圆柱流致振动特性与圆柱间距密切相关[10],Kim等[11]实验发现当双圆柱距离超过2.7倍圆柱直径时,上游圆柱振动规律与单圆柱流致振动相似;关德宝等[12]试验发现,下游圆柱振幅随圆柱间距的增加先增大后减小。由于双圆柱流致振动问题本身的复杂性,大部分研究都以实验为主。在非线性流固耦合问题的数值研究中,关键在于流体和钝体之间的移动边界的处理,任意拉格朗日-欧拉方法是目前比较成功的用于解决移动边界问题的方法[13]。但是,当涡致振动或驰振发生时,钝体具有较高振幅,传统的动网格方法已无法满足计算需要。
为充分了解多钝体的流致振动规律,本文采用拓扑网格变形技术,结合耦合界面,实现流体与多个运动钝体之间的耦合计算。分别对二维双圆柱和三圆柱、三维双圆柱模型进行了数值计算,得到了圆柱的振幅和频率响应,观察圆柱尾流旋涡结构,并与实验进行比较分析。
1 物理模型
当弹性支撑的钝体产生流致振动时,横向振幅远大于流向振幅,因此本文仅考虑钝体的横向振动,针对两个或两个以上钝体的流致振动展开研究。以串行排列双圆柱物理模型为例,如图1所示,每个振动系统的主要参数有:刚性圆柱的直径为D、长度为L,支撑弹簧的弹性系数为K和摩擦等引起的系统阻尼为C。本文在圆柱表面增加附属粗糙带,以此加强柱体流致振动[14]。双圆柱轴心距离为d,均为单自由度振动系统,振动方向垂直于来流速度和圆柱轴向。

图1 物理模型Fig.1 Physical model
2 数值方法
2.1 流体控制方程
本文通过求解非稳态雷诺平均纳维-斯托克斯方程组(Unsteady Reynolds-averaged Navier-Stokes),获得绕流弹性支撑多钝体流场的数值解。不可压缩流体的连续性方程和动量方程为
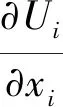
(1)
(2)
式中:Ui为平均流速;v为分子运动黏度;Sij为应变率张量
(3)
τij=2vTSij
(4)
式中湍动黏度vT的相关定义为
(5)
(6)

(7)
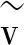
(8)
为了使时间和空间上的数值离散具有二阶精度,发散项、梯度项和对流项采用二阶高斯积分格式,时间积分采用二阶向后欧拉积分法,动量方程和连续性方程的求解采用压力隐式算子分裂算法。
2.2 流致振动控制方程
流场中的振动圆柱简化为质量-弹簧-阻尼系统,其单自由度振动方程为

(9)
式中:m为振动系统总的惯性质量,由振动柱体质量和三分之一弹簧质量组成;f(t)为垂直流向的流体作用力,在计算过程中通过对圆柱表面的压力和黏性力积分获得。运动方程采用二阶混合显隐式时间积分法进行求解,过程为
(10)
(11)
yn+1=yn+Δt·vn+1
(12)
2.3 网格模型
由于弹性支撑多钝体绕流的流固耦合问题本身的复杂性,多钝体流致振动的数值模拟方法还需进一步优化。在弹性支撑多钝体流致振动数值计算过程中,为了实现钝体与流体介质之间作用力和运动关系的传递,需要不断调整运动壁面区域的计算网格。为了减小因网格扭曲而引起的计算误差,本文网格模型采用了耦合界面(Coupling Interface,CI)[16]和拓扑网格变形技术[17-18]。拓扑网格是一种底层静态的网格,该网格本身并不随运动子块产生运动,不会因拉伸或挤压产生网格形变,其特点在于子块区域外围网格会随子块运动而自动生成或崩塌消失。将每一个柱体附近计算区域划分成方形网格子块,柱体位于子块中心。在流致振动发生时,子块内网格随钝体壁面整体运动,子块上下网格通过拓扑网格变形技术进行更新;子块左右通过CI界面与上下游计算区域网格连接,实现多柱体流致振动的数值模拟。CI界面用来连接多个不连续网格区域,不要求相邻界面的网格节点一一匹配。在具有旋转部件的数值计算中要求所有界面网格相互匹配往往非常困难,CI界面是处理这类问题的有效途径。对于界面网格不连续的区域,分别进行网格划分,然后使用一个或者多个CI界面进行连接。与滑移网格不同,CI界面包含主界面和副界面,使用加权插值进行流率计算和传递。
为避免柱体运动造成网格拉伸或挤压变形,保证在数值计算过程中维持较高的网格质量,通过网格拓扑变形技术实现运动子块上下网格的自动生成或塌缩,避免网格单元体积的剧烈变化。如图2所示,振动柱体所在子块的上下侧为动态层,h为动态层与邻近网格(n)的距离。当流致振动发生时,子块内网格整体运动,过程如下:
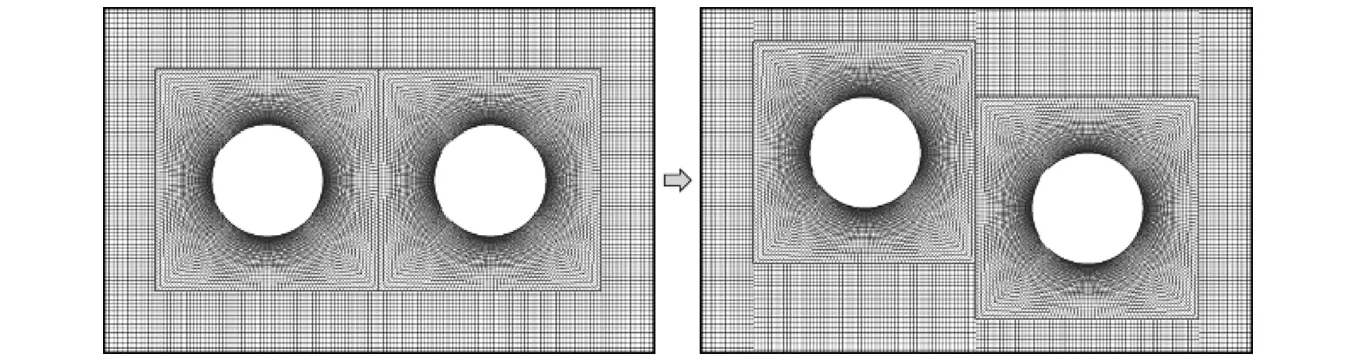
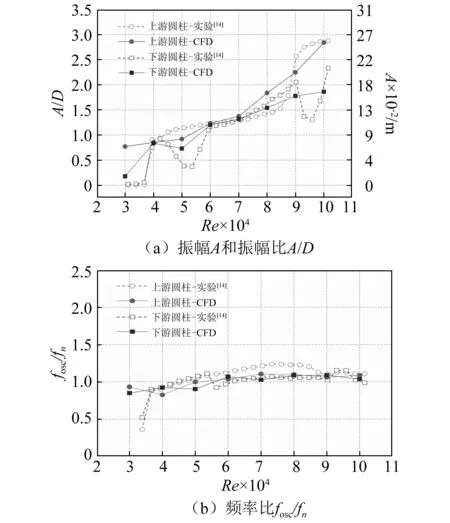
(a)子块向上运动时,h变小,当h (b)子块向下运动时,h增大,当h>hmax时,将会自动生成网格n-1。 其中hmin和hmax分别是根据整体网格质量而设定的最小和最大网格厚度。拓扑变形技术能自动对网格进行更新,有效解决旋转、拉伸和挤压造成的网格变形问题,有效减小网格变形造成的计算误差。 图2 拓扑网格及耦合界面Fig.2 Topological mesh and coupling interface 为了研究弹性支撑多钝体的流致振动响应特性,同时验证本文提出的数值方法尤其是动网格模型的可靠性,本文分别对二维双圆柱和三圆柱、三维双圆柱模型进行了数值计算。 二维双圆柱计算区域如图3所示,顶部和底部距离为9D,与实验水深相同,速度入口距上游圆柱轴心为25D,下游圆柱轴心距离压力出口为25D,两种不同间距的串列双圆柱模型的轴心间距d分别为2D和2.5D。顶部和底面为壁面边界。为了强化圆柱的流致振动,在圆柱表面沿轴向安装两条附属粗糙带,粗糙带覆盖16°圆柱表面,厚度为0.847 mm,数值计算中采用壁面函数进行求解。本文计算采用结构化网格,均经过网格无关性验证,并将计算结果与实验进行比较。 图3 计算区域及边界条件Fig.3 Calculation region and boundary conditions 3.1.1 双圆柱轴心距离d=2D 当串列双圆柱轴心距离d=2D时,双圆柱所在方形网格子区域之间存在共用耦合界面。当圆柱发生流致振动时,圆柱所在子区域整体运动,并在动态层经过区域成功实现网格自动崩塌与生成,如图4所示。计算雷诺数(Re)范围为3×104≤Re≤10×104,对应折减速度(U*=U/fnD)范围为3.84≤U*≤12.81,fn为上游圆柱固有频率。 图4 串列双圆柱流致振动网格变化(d=2D)Fig.4 Mesh changes of two cylinders in tandem(d=2D) 双圆柱流致振动的振幅和频率响应如图5所示,数值结果与实验值基本吻合。双圆柱振动响应曲线明确显示出流致振动的各个分支:涡致振动(Vortex Induced Vibration, VIV)初始分支(3×104≤Re<4×104)、上部分支(4×104≤Re<8×104)、过渡分支(8×104≤Re<9.5×104)和驰振(Re≥9.5×104)。当Re<3×104时,在实验和数值模拟中都没有观察到圆柱发生流致振动。在涡致振动初始分支,上游圆柱振幅的数值结果较实验值高,这是由于本文将圆柱振动系统阻尼简化为线性阻尼,与实际的非线性阻尼存在差异[19],而该差异在流速较低时表现尤为明显,使计算中涡致振动初始分支的激发速度小于实验中初始分支的激发速度。当振动处于涡致振动上部分支的初始段(4×104≤Re<5.5×104)时,实验结果显示下游圆柱振幅陡降,几乎降至0值附近,这是由于下游圆柱的振动受到上游圆柱振动和自身旋涡脱落的共同作用,当Re≤4×104时,下游圆柱主要受上游圆柱振动的影响,表现出与上游圆柱相似的频率和振幅响应;当Re=5×104时,下游圆柱振动频率突降,低于上游圆柱振动频率,下游圆柱振幅明显下降;当Re≥5.5×104时,下游圆柱主要受自身旋涡脱落的影响,频率和振幅逐渐上升。但是数值模拟中却没有捕捉到此现象,这是由于圆柱振动系统阻尼为线性阻尼,涡致振动初始分支更易激发,下游圆柱振动主要受自身旋涡脱落的影响,因而为表现出振幅和频率的明显波动。除了上部分支初始段的差异外,数值模拟和实验结果吻合较好。当Re≥9×104圆柱发生驰振后,振动频率比稳定在1.0左右,模拟值与实验值结果保持一致。 图5 串列双圆柱(d=2D)流致振动响应Fig.5 The FIM response of two cylinders in tandem(d=2D) 圆柱的近尾迹涡量分布是反应流致振动特性的重要参数,涡量分布进一步形成不同的圆柱尾涡结构,数值模拟在描述和分析圆柱尾涡结构时具有极大优势。由双圆柱振幅频率响应(见图5)分析可知,Re=3×104时,上下游圆柱位于初始分支,从图6(a)中可以清晰观察到上游圆柱的旋涡脱落为2S模式。两个旋涡随流体向下游移动,在通过下游圆柱区域时,顺时针旋转的旋涡紧贴下游圆柱上侧移动,逆时针旋转的旋涡紧贴下游圆柱正下方移动。由于双圆柱之间的特定距离,导致来自上游圆柱的旋涡吸收了下游圆柱分离的旋转方向相同的旋涡,从而阻止下游圆柱大尺度Kármán旋涡的形成,进而抑制流致振动的产生,这与实验现象相吻合。图6(b)所示为Re=6×104时的近尾迹旋涡结构,上下游圆柱均为2P形态,即一个振动周期内脱落两对旋涡,这与Khalak等[20]在涡致振动上部分支观察到的圆柱尾涡形态相同。图6(c)所示为Re=9.3×104时的近尾迹旋涡结构,此时双圆柱流致振动由涡致振动向驰振过渡。对于上游圆柱,大部分振动周期为2P+2S模式,尾涡具有多种形态,但在某些周期内,上游圆柱在上行过程中会多脱落一个附加旋涡。由于受到来自上游圆柱旋涡的强烈干扰,下游圆柱的尾涡形态难以捕捉。图6(d)所示为Re=10×104时的近尾迹旋涡结构,在一个振动周期内,上游圆柱产生的脱体旋涡高达8个,但是下游圆柱由于受到上游圆柱的严重影响,尾涡形态不易观察。由以上分析可见,采用本文数值方法能有效描述双圆柱流致振动。 图6 d=2D时串列双圆柱尾涡结构Fig.6 Vortex structure of two cylinders in tandem with d=2D 3.1.2 双圆柱轴心距离d=2.5D 当串列双圆柱轴心距离d=2.5D时,上下游双圆柱所在网格子区域之间存在固定网格流场区域,包含两组耦合界面,这与d=2D的工况有所不同。如图7所示,在计算中拓扑网格成功实现了d=2.5D时双圆柱流致振动网格变化。 图7 串列圆柱流致振动网格变化(d=2.5D)Fig.7 Mesh changes of two cylinders in tandem(d=2.5D) 图8所示为上下游圆柱的振幅和频率响应曲线,可以观察到涡激振动的初始分支(3×104≤Re<4×104)、上部分支(4×104≤Re<8×104)、过渡分支(8×104≤Re<9.5×104)和驰振(Re≥9.5×104),在各个分支切换时,振幅和频率都发生了明显变化,与d=2D时双圆柱振动相比,d=2.5D时下游圆柱振动虽然也受到上游旋涡抑制,但抑制作用减弱,下游圆柱流致振动也因上游圆柱的存在表现出不同的振动特性。在涡激振动的初始分支,上游圆柱振幅的模拟数值也略高于实验值。当上游圆柱由涡致振动初始分支过渡到上部分支后,下游圆柱振幅随着Re增加而降低,并在Re=5×104附近出现极小值。Re>9.5×104时,上游圆柱发生驰振,下游圆柱振幅随Re增加先降低后增加,这是由于当Re≈9.5×104时,上游圆柱脱落的漩涡刚好附着于下游圆柱表面,抑制了下游圆柱漩涡的形成和脱落,从而使下游圆柱的振幅出现明显下降;在数值计算中也捕捉到了这一现象,因而下游圆柱表现出明显低于上游圆柱的振幅。在Re=5.5×104附近,实验结果显示下游圆柱频率突然降低,之后随Re增加缓慢增加。在涡致振动上部分支,实验和模拟结果均表明,上下游圆柱振动频率随着Re增加出现小幅度增大;当Re≥9.5×104时,上下游圆柱频率比均趋于稳定,最终稳定在1.0左右。 图8 串列双圆柱(d=2.5D)流致振动响应Fig.8 The FIM response of two cylinders in tandem(d=2.5D) 以Re=6×104时双圆柱振动为例,上下游圆柱振动均位于涡致振动上部分支。图9为d=2.5D时串列双圆柱尾流旋涡云图,从图中可以看出双圆柱的尾涡形态为2P,上游圆柱的尾涡形态较下游圆柱更为清晰。下游圆柱尾流旋涡在形成过程中受到来自上游圆柱的脱体旋涡影响,旋涡在演变过程中与来自上游的旋涡相互融合,进而使下游圆柱表现出明显区别于上游圆柱的振动特性。 图9 d=2.5D时串列双圆柱尾涡结构(Re=6×104)Fig.9 Vortex structure of two cylinders in tandem with d=2.5D(Re=6×104) 为了进一步验证本文数值方法的正确性,对二维三圆柱进行了数值模拟,相邻圆柱之间轴心距离d=2.5D,其余参数与二维双圆柱相同。图10所示为流致振动发生时,串列三圆柱网格变化情况,在整个计算过程中,网格并不发生扭曲变形,当柱体振幅较大时,可有效减少由此带来的计算误差。 图10 串列三圆柱流致振动网格变化(d=2.5D)Fig.10 Mesh changes of three cylinders in tandem(d=2.5D) 图11为三圆柱振幅和频率响应曲线,与二维双圆柱的结果相似,可以观察到流致振动依旧产生了四个分支,在各个分支切换时,振幅和频率变化明显。在涡致振动初始分支,上游圆柱和中间圆柱振幅的模拟值高于实验值。上游圆柱的振动受下游其他圆柱影响较小;与二维双圆柱相比,对应雷诺数下,上游圆柱的振幅变化也较小;上游圆柱最大振幅比A/D达到2.70。中间圆柱和下游圆柱则明显受到其他圆柱的影响,在Re=5×104附近,实验结果显示中间圆柱和下游圆柱振幅和频率突然降低,但振幅下降幅度明显小于二维双圆柱。当Re=9×104时,中间圆柱振幅出现明显波动,当Re>9.5×104时,振幅出现小幅下降;当Re>9×104时,下游圆柱振幅比逐渐稳定在2.5左右,而上中下游圆柱频率比均趋于稳定于1.0左右。 图11 串列三圆柱(d=2.5D)流致振动响应Fig.11 The FIM response of three cylinders in tandem(d=2.5D) 为深入分析不同间距、数量对圆柱流致振动的影响,图12对双圆柱(d=2D,d=2.5D)和三圆柱(d=2.5D)流致振动三组工况的振幅和频率响应进行了对比。三组工况中上游圆柱振幅的主要区别体现在涡致振动上部分支和过渡区域。如图12(a)所示,在上部分支(如Re=5×104),对于双圆柱工况,d=2D上游柱体振幅明显高于d=2.5D对应振幅,三圆柱工况中上游圆柱振幅最大;在过渡区域(8×104≤Re<9.5×104),d=2.5D双圆柱和三圆柱的上游圆柱振幅均高于d=2D双圆柱;Re=1×105驰振发生时,三组工况上游圆柱振幅均达到2.5D以上。对于双圆柱工况中的下游圆柱,在Re=3×104时柱体均无明显振动;在Re=5×104时,由于上游圆柱的影响,d=2.5D对应下游圆柱振幅出现降低;当柱体发生驰振时,d=2D对应下游圆柱振动加强,最大振幅远高于d=2.5D工况。值得注意的是,三圆柱的中间圆柱与d=2.5D双圆柱的下游圆柱位置类似,除了Re=3×104时,振幅变化趋势极为相似;受到第三柱体的影响,中间圆柱在Re=3×104时振动激发,振幅明显高于双圆柱下游圆柱。对于三圆柱的下游圆柱,由于上游两圆柱的存在,振幅相对较低,振幅响应曲线与其他圆柱有明显区别。对于三组工况的频率响应特性,主要区别体现在雷诺数较小时(Re≤5×104),如图12(b)所示。当Re=4×104时,双圆柱(d=2D)和三圆柱的上游圆柱的频率高于d=2.5D时;随着雷诺数增大,上下游圆柱频率比趋势吻合,最终稳定在1.0左右。由于三圆柱相互影响,当Re=8×104时,三圆柱频率不匹配,上游圆柱频率比最大,中间圆柱频率比最小。 图12 串列双圆柱(d=2D,d=2.5D)、 三圆柱(d=2.5D)流致振动响应Fig.12 The FIM response of two cylinders (d=2D,d=2.5D) and three cylinders (d=2.5D) in tandem 本文数值方法也可用于进行三维多柱体流致振动计算,与二维计算相比,三维模拟需要更高的硬件条件,而且需时更长。图13为三维双圆柱计算模型,计算区域尺寸24D×11D×6D,上游圆柱轴心距离入口7D,圆柱轴心间距d=2D,圆柱长L=4D。流道四周均为壁面边界,入口为均匀来流,出口为压力出口。 图13 三维双圆柱计算模型Fig.13 Calculation model of 3-dimensional two cylinders 图14所示为三维双圆柱发生流致振动时的网格变化情况。计算过程中,圆柱所在长方体区域随圆柱振动发生整体移动,并伴随网格自动生成与崩塌。图15所示为三维双圆柱流致振动响应曲线,上下游圆柱出现了明显的振动分区。在涡激振动初始分支,上游圆柱振幅明显降低,更加趋于实验数值。在Re=5×104附近,下游圆柱振幅出现小幅下降,但仍然高于实验数值;下游圆柱振动频率与上游圆柱近似,并未捕捉到试验中下游圆柱振动频率突降的现象。当Re≥9×104时,上下游圆柱产生驰振,上下游圆柱振动频率逐渐稳定,最终稳定在1.0附近,与实验结果相吻合。结合图5可知,三维计算中上下圆柱振幅和频率响应曲线与二维计算相比更接近实验结果。由此可见,三维计算结果更接近于实验值,证明了本文数值方法对于计算三维多圆柱流致振动的可行性。 图14 三维双圆柱流致振动网格变化(d=2D)Fig.14 Mesh changes of 3-dimensional two cylinders in tandem(d=2D) 图15 三维双圆柱流致振动响应Fig.15 The FIM response of 3-dimensional two cylinders 本文针对弹性支撑的多钝体流致振动进行数值分析,获得多钝体流致振动规律,并与实验进行比较,得出以下结论: (1)采用耦合界面结合拓扑网格技术,对弹性支撑多钝体流致振动进行二维和三维计算,数值结果与实验结果相吻合,证明该方法是处理高振幅多钝体流致振动的有效方法。 (2)对于d=2D的串列双圆柱流致振动,圆柱振幅和频率响应的数值结果与实验测试趋势基本一致,能清晰观察到涡致振动初始分支和上部分支,并且当Re>8×104时,振动由涡致振动向驰振过渡;Re≥9.5×104时,流致振动发展为驰振,上下游圆柱振幅降低,频率比稳定在1.0左右。另外,圆柱尾涡形态随流致振动分支切换发生变化,当驰振发生时,下游圆柱的尾涡形态受上游圆柱影响难以捕捉。 (3)对于d=2.5D的串列双圆柱流致振动,数值模拟与实验结果清晰显示出流致振动各个分支。与d=2D相比,Re=3×104时下游圆柱受到上游圆柱的抑制作用减弱。Re=6×104时,双圆柱尾涡结构与d=2D时相同,上下游圆柱均为2P模式。 (4)对于d=2.5D的串列三圆柱流致振动,依旧可以观察到流致振动的各个分支。上游圆柱受到其下游圆柱的影响较小;在Re=5×104附近,中间圆柱和下游圆柱取得最小值,在Re=9×104附近,中间圆柱振幅出现明显波动,下游圆柱振幅逐渐趋于稳定。 (5)与二维模拟相比,本文数值方法对三维高振幅多柱体流致振动仍能进行有效计算,所得结果更为接近实验值,但三维计算需要更高的硬件条件,如何提高三维计算速度将是下一步研究工作的重点。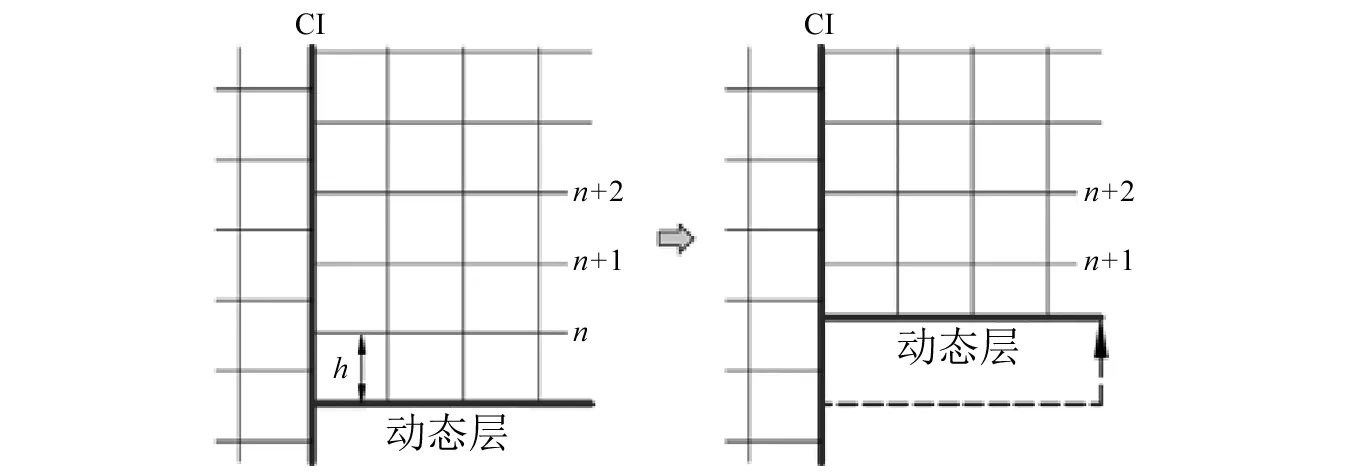
3 结果与讨论
3.1 二维双圆柱流致振动





3.2 二维三圆柱流致振动



3.3 三维多柱体流致振动



4 结 论

