含逆变回馈装置的城市轨道交直流混合潮流计算

刘 炜， 许伶俐， 廖 钧， 刘 聪， 刘瑞龙

(1． 西南交通大学 电气工程学院， 四川 成都 610031； 2． 中国铁路设计集团有限公司 电化电信院， 天津 300142)

近些年来，列车再生制动技术在城市轨道中的应用逐渐普遍。重庆、北京、南京等地铁供电系统都采用了逆变回馈装置吸收和再利用列车再生制动能量[1-2]。以上海地铁3、4号线单列车牵引、制动能耗测试为例，列车再生制动能量占牵引能量的35%～56%[3]，再生制动能量利用技术应用前景广泛。低压400 V和中压35/10 kV逆变回馈装置在国内的城市轨道中应用较多。现阶段，含逆变回馈装置的城市轨道潮流计算方法尚不成熟，逆变回馈装置的选址和容量设计成为亟需解决的问题。

城市轨道交直流混合潮流计算可分析再生制动能量在低压供电系统、中压网络和110 kV电力系统的分布，评估再生制动能量利用率，计算逆变回馈装置的投资回报周期，优化逆变回馈装置的系统设计。文献[4-5]建立了基于整流机组模型的城市轨道交直流统一牵引供电算法，并研发了包含模拟列车运行、直流牵引供电系统潮流计算及交直流牵引供电系统潮流计算的仿真平台DCTPS。文献[6-8]将城市轨道整流机组和逆变回馈装置按照晶闸管换流器统一建模，将牵引变电所视为PQ节点，采用交直流交替迭代的方法进行城市轨道供电系统的潮流计算。但是逆变回馈装置为电压源型换流器(VSC)[9-10]，晶闸管换流器模型不再适用，当逆变回馈装置处于逆变状态时，电压方向不变，直流侧电流方向改变[11-12]。

本文综合考虑逆变回馈装置的潮流计算模型和投入策略，研究城市轨道交直流混合潮流计算方法，仿真多列车在线路上运行时的牵引网网压和牵引变电所负荷过程，计算再生制动能量在邻近列车和逆变回馈装置之间的分配以及反馈能量在交流供电系统中的分布，分析逆变回馈装置启动电压及列车发车密度对节能效果的影响。

1 城市轨道牵引变电所建模

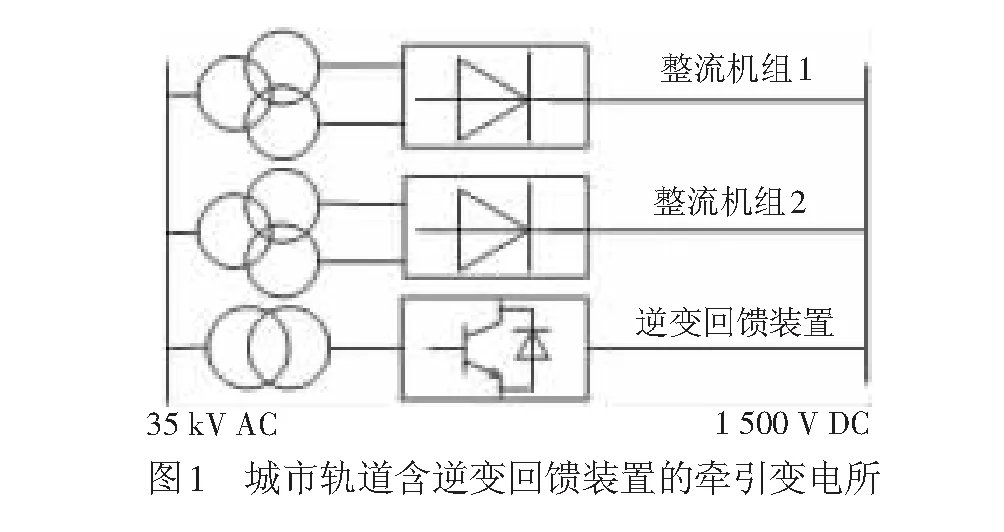
城市轨道牵引变电所采用并列运行2台12脉波整流机组，以24脉波形式输出实现交流到直流的能量变换[12-13]。逆变回馈装置接入直流牵引网，直流牵引网上剩余的再生制动能量经逆变回馈装置、隔离变压器回馈到35/10 kV中压网络或400 V低压网络[12]。城市轨道含逆变回馈装置的牵引变电所见图1。

2 整流机组的潮流计算模型

2.1 整流机组数学模型

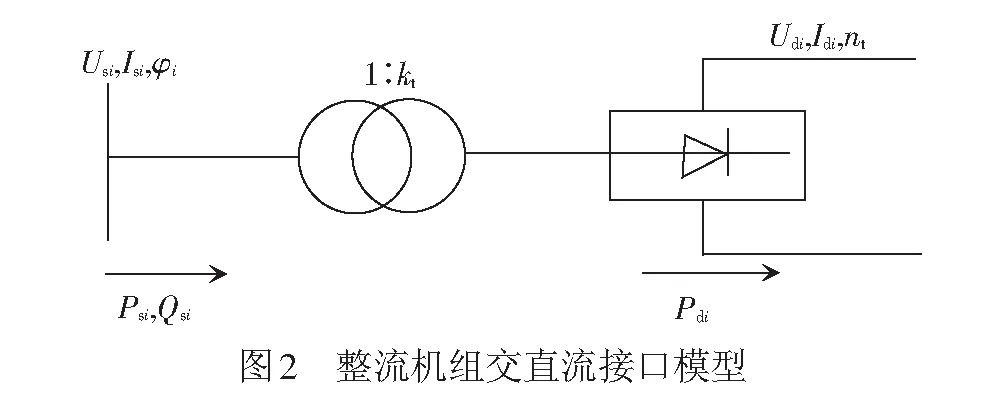
整流机组的交直流接口模型见图2。Isi为整流机组交流侧电流幅值；Usi为整流机组交流侧节点电压幅值；φi为整流机组的功率因数角；Idi为整流机组直流牵引侧节点电流；Udi为整流机组直流牵引侧节点电压；Psi、Qsi为整流机组交流侧有功功率、无功功率；nt为整流器桥数；kt为整流变压器的变比；Pdi为整流机组直流牵引侧功率。

忽略移相等过程影响，城市轨道整流机组的数学模型为[14-15]。

( 1 )

( 2 )

式中：kγ为常数，取0.995；24脉波整流机组nt=4；XC为单桥换流电抗。

2.2 修正方程

对于普通交流母线节点，其功率偏差方程可与一般潮流计算式相同。对于与整流机组关联的交流侧节点，建立修正方程为

( 3 )

式中：Ui、Uj分别为交流侧节点i、j的节点电压;Gij、Bij分别为i、j节点之间的电导和电纳；δij为i、j节点之间的相角差；Pi、Qi分别为i节点的注入有功、无功功率；na为除牵引变电所外的交流节点的数目；nb为处于整流状态时，牵引变电所的数目；nc为处于关断状态时，牵引变电所的数目；nd为处于逆变状态时，牵引变电所的数目。

对于整流机组直流牵引侧节点，直流侧修正方程为

( 4 )

式中:ne为列车节点的数目；Git为直流侧节点i和节点t之间的电导。

整流机组直流侧节点电压Udi用Idi、φi分别由式( 1 )、式( 2 )表示，Udi的2个修正方程式为

( 5 )

( 6 )

式中：Δd1i、Δd2i分别为Udi用Idi、φi表示的修正量。

3 逆变回馈装置的潮流计算模型

3.1 数学建模

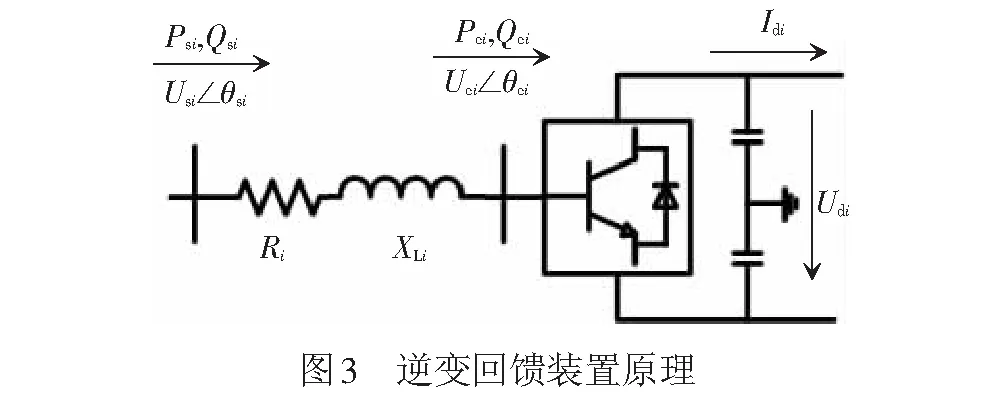
逆变回馈装置主要包含逆变器、逆变电抗器、直流电容器等。本文对逆变回馈装置采用电压源型换流器(VSC)建模，逆变回馈装置原理见图3。假设逆变回馈装置交流侧接入点的电压和注入功率为Usi∠θsi(θsi为交流侧节点电压相角)，Psi+jQsi；逆变器等效阻抗为Ri+jXLi，VSC交流侧的电压和注入功率为Uci∠θci(θci为换流桥侧节点电压相角)，Pci+jQci，VSC直流侧的电压和注入电流为Udi、Idi。

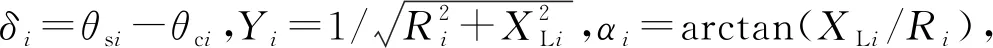
( 7 )

( 8 )

VSC直流侧功率方程为[16-17]

( 9 )

式中：μi为直流电压利用率，μi∈(0,1]；Mi为调制度，Mi∈[0,1]。

3.2 控制方式

逆变回馈装置在城市轨道交通供电系统中一般有如下控制方式：(1) 定直流侧节点电压Ud和交流侧节点电压Us控制，此时逆变回馈装置工作在吸收剩余再生制动能量，稳定牵引网网压状态；(2) 定直流侧节点电压Ud和交流侧无功功率Qs控制，此时逆变回馈装置兼顾补偿无功功率；(3) 定交流侧有功功率Ps和交流侧电压Us控制，此时需要吸收的再生制动功率超过了逆变回馈装置的过载能力，逆变回馈装置工作在最大能力运行状态。

3.3 修正方程

逆变回馈装置交流节点的功率修正方程考虑了换流器与交流母线节点之间的功率交换关系，修正方程为

(10)

(11)

(12)

对逆变回馈装置的直流侧节点，其直流网络修正方程仍为式( 4 )。

4 交直流交替迭代潮流计算

4.1 直流侧

城市轨道供电系统直流侧节点包括列车节点、牵引变电所直流侧节点。对于列车节点的注入电流由牵引计算或者实测获得[5]。列车处于牵引工况时，从接触网取流注入钢轨，当列车处于制动工况时，制动反馈电流注入接触网。

城市轨道直流侧潮流计算修正方程为

[ΔIdb,Δd1,Δd2,ΔIdc,ΔIdd,Δd3,

Δd4,Δd5,ΔIde]T=

J[Idb,Udb,φdb,Udc,Idd,Udd,mdd,δdd,Ude]T

(13)

式中：J为雅可比矩阵；

ΔIdb=[ΔId1,ΔId2,…,ΔIdnb]T

ΔIdd=[ΔId1,ΔId2,…,ΔIdnd]T

ΔIde=[ΔId1,ΔId2,…,ΔIdne]T

Δd1=[Δd1i,Δd1i,…,Δd1nb]T

Δd2=[Δd2i,Δd2i,…,Δd2nb]T

Δd3=[Δd3i,Δd3i,…,Δd3nd]T

Δd4=[Δd4i,Δd4i,…,Δd4nd]T

Δd5=[Δd5i,Δd5i,…,Δd5nd]T

Idb=[Id1,Id2,…,Idnb]T

Udb=[Ud1,Ud2,…,Udnb]T

φdb=[φd1,φd2,…,φdnb]T

Udc=[Ud1,Ud2,…,Udnc]T

Idd=[Id1,Id2,…,Idnd]T

Udd=[Ud1,Ud2,…,Udnd]Tmdd=[md1,md2,…,mdnd]T

δdd=[δd1,δd2,…,δdnd]TUde=[Ud1,Ud2,…,Udne]T

其中，mi为调制参数，mi=μiMi。

牵引变电所工作在整流状态时，待求变量为整流机组的直流侧电压、电流和功率因数角；牵引变电所工作在逆变回馈状态时，待求变量为直流侧电压、电流和逆变回馈装置相角差、调制参数。

4.2 交流侧

当城市轨道牵引变电所工作在整流状态时，在交流侧潮流计算中看做PQ节点，节点功率由直流侧潮流算法计算得到。当牵引变电所工作在逆变状态时，可看做PV节点，节点注入有功功率由式( 7 )计算。交流侧潮流计算更新城市轨道牵引变电所35 kV和车站400 V侧电压。

4.3 交直流交替迭代

牵引网网压是逆变回馈装置投切策略的重要判断依据。潮流计算中，每次迭代需要判断牵引所直流牵引网网压Udi，牵引变电所不同工作状态的判断条件为

(14)

式中：Ud0为整流机组空载电压；Udset为逆变回馈装置的启动电压。

交直流交替迭代的思路可以用于城市轨道含逆变回馈装置的交直流潮流计算。收敛条件为

(15)

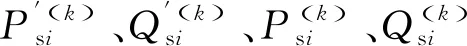
含逆变回馈装置的城市轨道交直流交替迭代潮流计算流程，见图4。

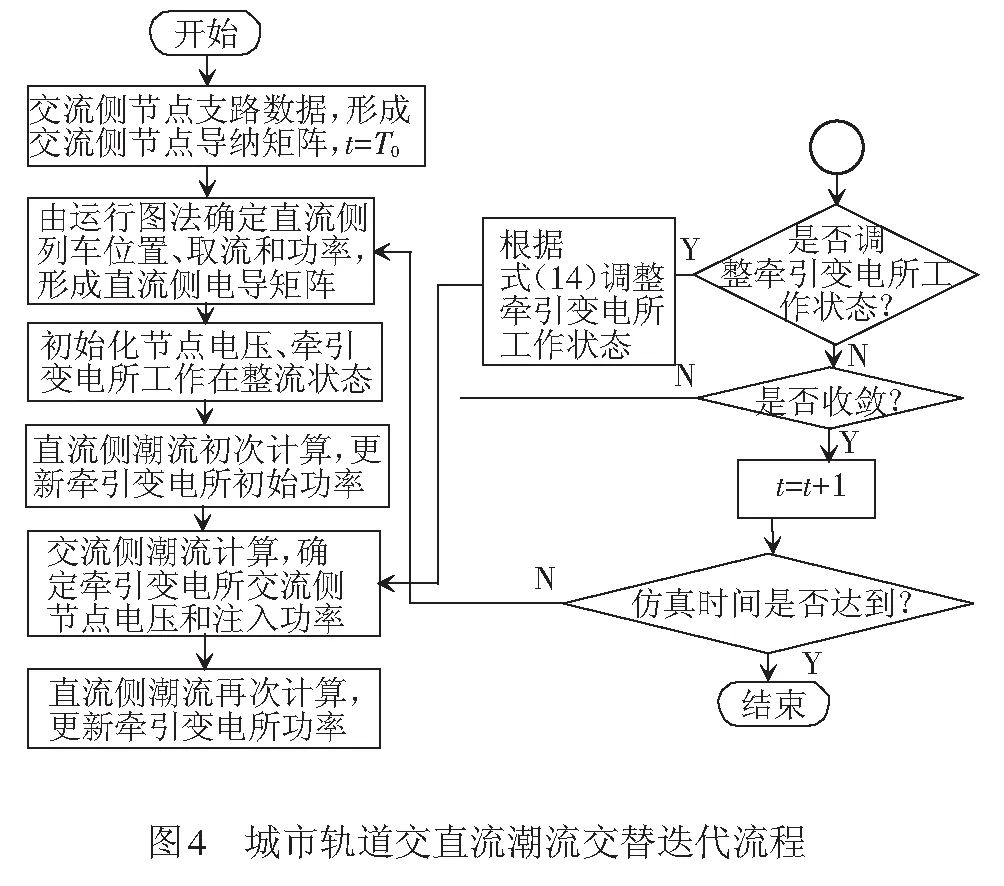
5 工程实例

某地铁线路的供电系统见图5，其中包含MT1、MT2主所以及Sub1～Sub7牵引所。

整流机组额定功率均为2×3 300 kVA；接触网电阻为0.014 3 Ω/km，钢轨电阻在考虑5%磨耗的情况下设为0.02 Ω/km。主所中，变压器变比为110/38.5 kV，主变压器容量为2×25 MVA，联结方式为YNd11，短路阻抗10.5%，空载损耗10.5%。电缆参数见表1。

表1 电缆参数

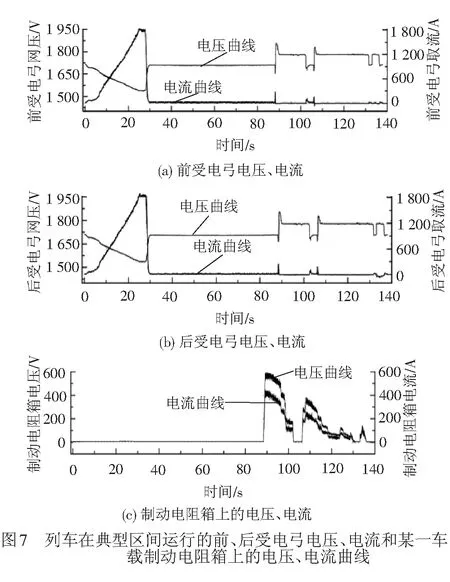
通过实际测试可以获得列车运行过程的取流与位置关系， 列车负荷过程监测见图6。利用多普勒雷达采集列车速度和位置信息。列车负荷过程实测在夜间单车进行。载荷为AW2，通过沙袋进行模拟，列车按照正常运营时的速度指导曲线运行。通过霍尔电压、霍尔电流传感器，同步采集2处列车受电弓电压、电流和4个车载制动电阻箱电压、电流。

在典型区间运行的列车受电弓电压、电流，某一车载制动电阻箱电压、电流(平均值)曲线见图7。

列车再生制动反馈功率可以用单列车运行时车载制动电阻上消耗的功率等值。全线安装35 kV逆变回馈装置，发车对数为12对/h。当逆变回馈装置启动电压Udset均设置为1 730 V时，当T=223 s时的列车位置和取流分布结果见表2。

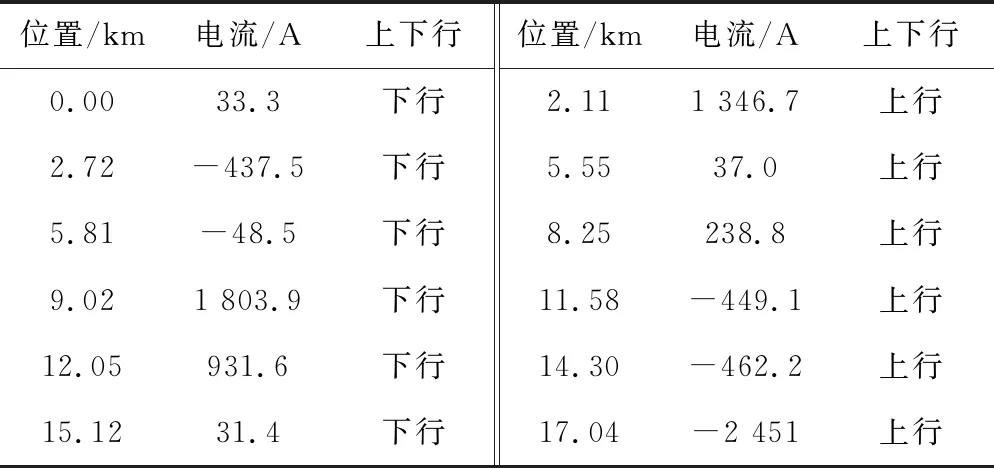
表2 T=223 s列车负荷分布

供电计算采用本文给出的含逆变回馈装置的城市轨道交直流交替迭代潮流算法进行，算法迭代次数为13次。上下行列车、牵引所母线电压分布见图8，其中，再生制动工况用虚线圆圈内的矩形黑点表示。由图8可以看出，处于整流状态的为Sub1～Sub4，处于关断状态的为Sub5、Sub6，处于逆变状态的为Sub7。

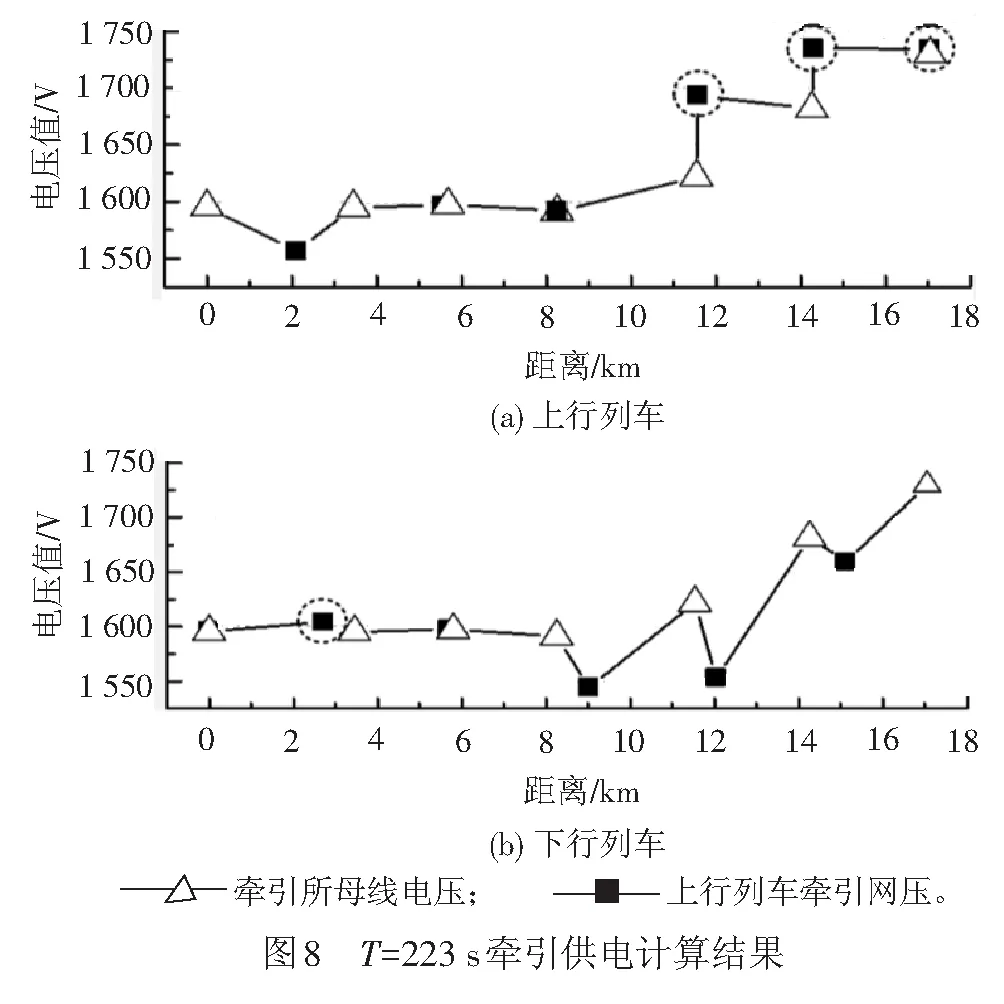
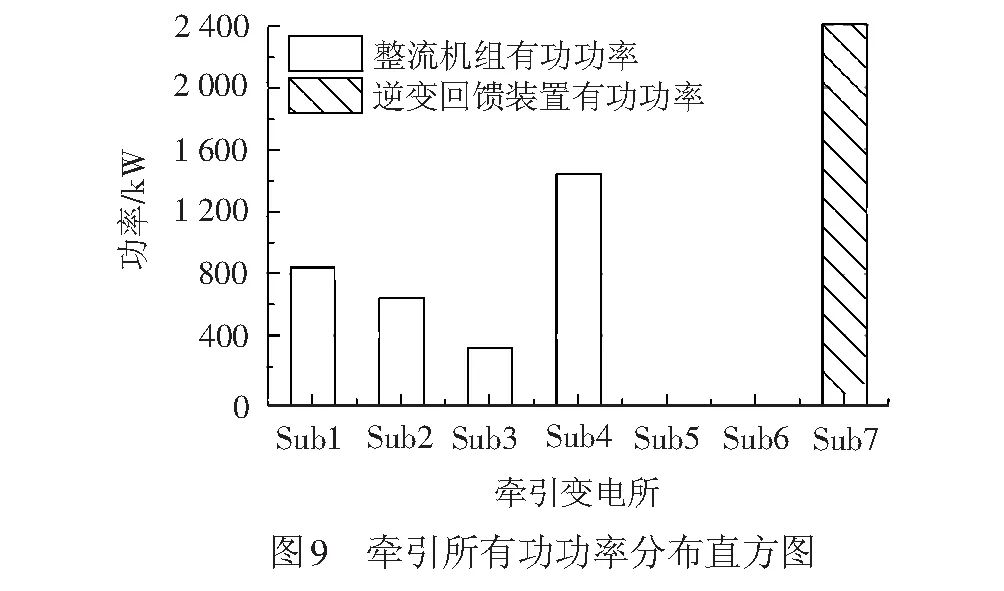
对应时刻的Sub1～Sub7牵引变电所的交流侧有功功率见图 9。

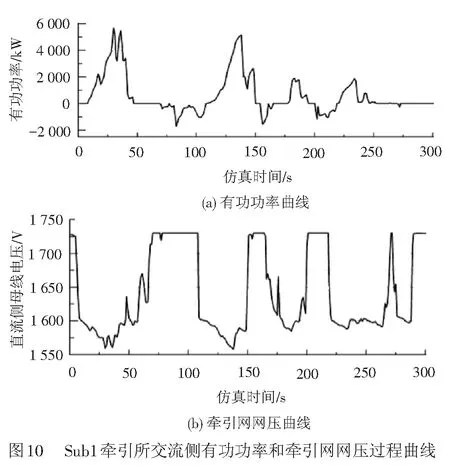
发车间隔300 s时，Sub1的交流侧有功功率变化和牵引网网压变化曲线见图10。

定义W1为全线牵引所逆变回馈能量，W2为牵引能量，W3为所有列车再生制动能量总量，可得

(16)

(17)

式中：η1为全线牵引变电所逆变回馈能量占牵引能量的比例；η2为全线牵引变电所逆变回馈能量占所有列车再生制动能量总量的比例。

对发车对数为12对/h的运行工况进行仿真，可以得到W1为832.41 kW·h，W2为5 496.6 kW·h，W3为2 599.1 kW·h，η1=15.1%，η2=32.03%。

情形1不同逆变回馈装置启动电压对节能效果的影响。在相同发车对数，不同逆变回馈装置启动电压下回馈能量的统计见表3。

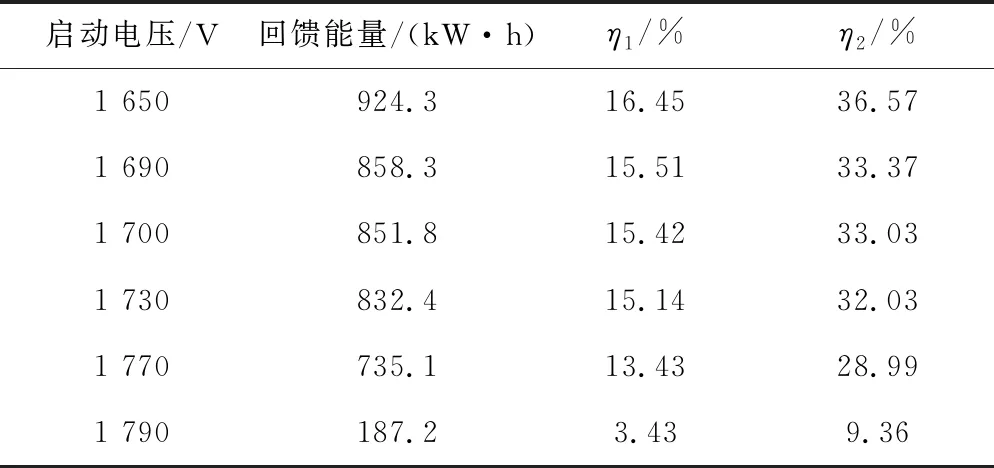
表3 不同逆变回馈装置启动电压下回馈能量统计

逆变回馈装置启动电压对列车再生制动能量的吸收利用有着重要影响。当启动电压较低时，本该优先被邻近车吸收的部分制动能量被反馈到中压网络。当启动电压升高至一定水平时，邻近列车可以优先利用列车再生制动能量。约70%左右的列车再生制动能量由邻近处于牵引工况的列车吸收，剩余部分被地面逆变回馈装置反馈至交流电网。但如果设置了过高的逆变回馈装置启动电压，列车制动时所在位置处的牵引网电压升高至车载制动电阻启动电压，列车再生制动失效。

情形2不同发车对数对节能效果的影响。不同发车对数情况下逆变回馈能量统计见表4。

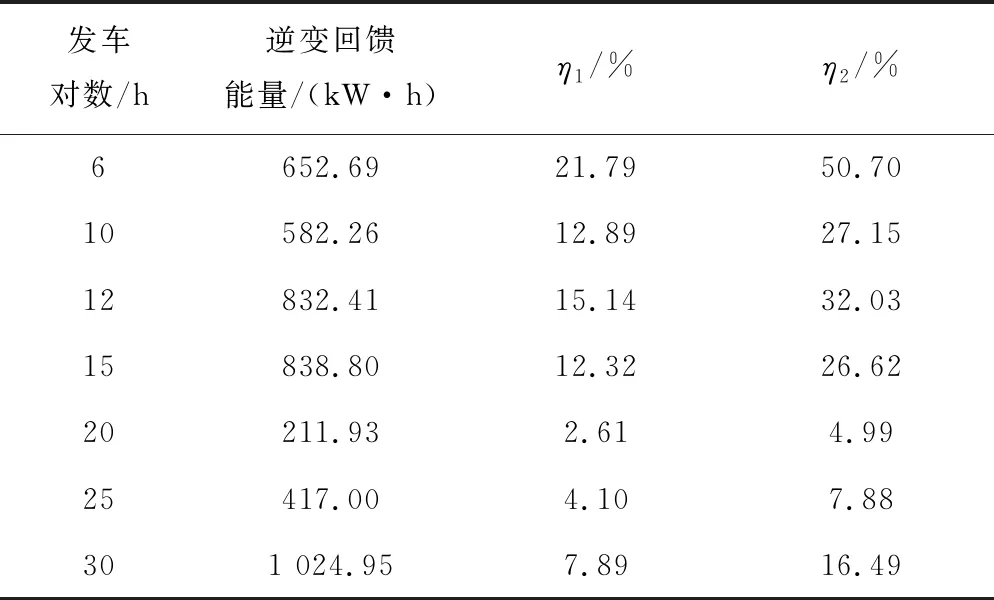
表4 不同发车对数情况下回馈能量统计

当发车密度较低时，邻近车吸收的再生制动能量较少，主要由逆变回馈装置反馈再生制动能量，此时η1较高；当发车密度逐渐增加，增加到20对/h时，主要由邻近列车相互吸收再生制动能量，η1下降；当发车密度继续增加，牵引网上列车再生制动能量总量较大，η1会有所上升。评估逆变回馈装置在供电系统中的节能效果，不能仅统计高峰小时的回馈能量，应综合考虑包含不同发车密度和持续时间的全日行车计划，以日回馈能量作为考核指标。

6 结论

本文建立了逆变回馈装置的交直流变换模，结合逆变回馈装置的投切策略和潮流控制方式提出了含逆变回馈装置的城市轨道交直流混合潮流计算算法。通过列车负荷过程实测和实际供电系统工程案例仿真计算，分析了逆变回馈装置节能效果的影响因素。

(1) 在城市轨道供电系统的潮流计算中，牵引变电所的计算模型以牵引网网压为依据，在整流机组模型和逆变回馈装置模型之间切换。逆变回馈装置采用电压源型换流器建模，城市轨道交直流混合潮流计算采用交直流交替迭代的算法。

(2) 列车再生制动能量在邻近列车、逆变回馈装置以及车载制动电阻之间分配。列车再生制动能量的分配受到逆变回馈装置启动电压影响。启动电压越高，邻近车吸收再生制动能量的效果会越好。但过高的启动电压会导致车载制动电阻频繁启动，甚至造成列车再生制动失效。

(3) 发车密度影响逆变回馈装置的节能效果。对于逆变回馈装置的节能效果评估，应以日回馈能量作为考核指标，综合考虑包含不同发车密度和持续时间的全日行车计划对节能效果的影响。