析错因思策略获方法
摘 要:講评试卷是数学教学中必不可少的常规环节,是反馈与调控学生知识技能、思想方法和掌握情况的重要手段,但当前小学毕业阶段的试卷讲评还存在“高投入低效益”的问题。基于此,本文通过“把脉”学生答题错因,从结果与过程这两个方面来谈试卷分析对策,以应对此阶段数学题综合性强的问题。
关键词:毕业试题;分析与讲评;分析对策
中图分类号:G427 文献标识码:A 文章编号:2095-624X(2019)25-0090-02
引 言
随着评价方式的转变,小学数学毕业阶段考查重心已由原来的偏重知识技能熟练程度的静态检测,转向了关注知识形成、操作验证、信息汲取等能力的动态检测。这种转变对学生在思考问题的深度和沟通知识点之间内在联系方面的观察、分析、切换信息能力都提出了新的要求[1]。然而,教学中的习题资料却未发生相应的转变,这导致学生在解决问题时错误百出,甚至无从下手。如何化解这一矛盾,提质保效呢? 笔者认为,教师可以从以下几方面做起。
一、结果与过程并重,以过程性突破“思维提升”
在试卷分析中教师如果就题论题,只关注学生答题的结果,不关注学生的思考过程,会造成教学上过多地关注用公式或规律解决问题,忽视公式和规律形成过程这一现象,而这恰恰是知识最本质、最核心的部分。应对过程性错误,教师可分三步展开。
1.追踪思维痕迹,“把脉”错误成因
对于过程性问题的检测,学生并不是完全不会解答。
错题呈现:圆的半径是4厘米,它的面积是( )平方厘米;如果把圆平均分成若干份,剪拼成一个近似的长方形,这个近似的长方形的长是( )厘米。
错误解法:2×4=8(cm)(人数较多)
错因分析:已知圆的半径,能求其周长和面积,但学生在学习圆的面积公式时没有完全明白圆转化成近似长方形后,它们之间有什么联系。所以,学生在解决第二个问题时,把“近似的长方形”的长算成是直径了。
从学生的错因分析中我们发现,学生的思维障碍就是在最抽象的一环,“圆周长的一半”怎么就等于近似长方形的长了?因此,安排学生自查分析错因,更能让教师准确“把脉”,进而针对性完善。
2.追寻问题本质,促进问题解决
教师应以学生自我分析为前提,再现知识的形成过程,促学生知其然,更能知其所以然。
错题呈现:根据6×4、6×4÷2,把图画完整(见图1)。
错误解法:没画或画错。
学生错因分析:一类学生表示没看懂题意,不知道怎样把算式与图形联系起来。
另一类学生表示看到“6×4”想到的是长方形的“长与宽”,所以把图形补成了长方形。
检测后发现:根据“6×4”画出“平行四边形”的占43%,画出“长方形”(见图2)的占38%,将近19%的学生有拼、有补,答错了。从此题发现:在平时练习时,学生已经习惯了已知底和高求面积,形成了一定的思维定式。因此,笔者以错题为媒介再次让学生经历知识形成的过程,从而实现自主构建。
3.整理归纳要点,提升思维深度
错题讲解分析后,及时跟进对知识点的整合和归纳,这是避免学生再次出错的重要步骤。教师可以引导学生采用“语言描述”的方法做一份“自我整理”,这不仅能帮助学生整理与小结解决问题的要点,而且是实现知识内化、思维提升的重要一环。
二、提取与切换合理应用,以分层操作突破“综合性强”
信息量大、综合性强是试卷命题发展的必然趋势。丰富、多元、综合的信息,可以培养学生分析、提取、整合信息的能力,但是也会造成学生审题时出现无法汲取有用信息的问题。
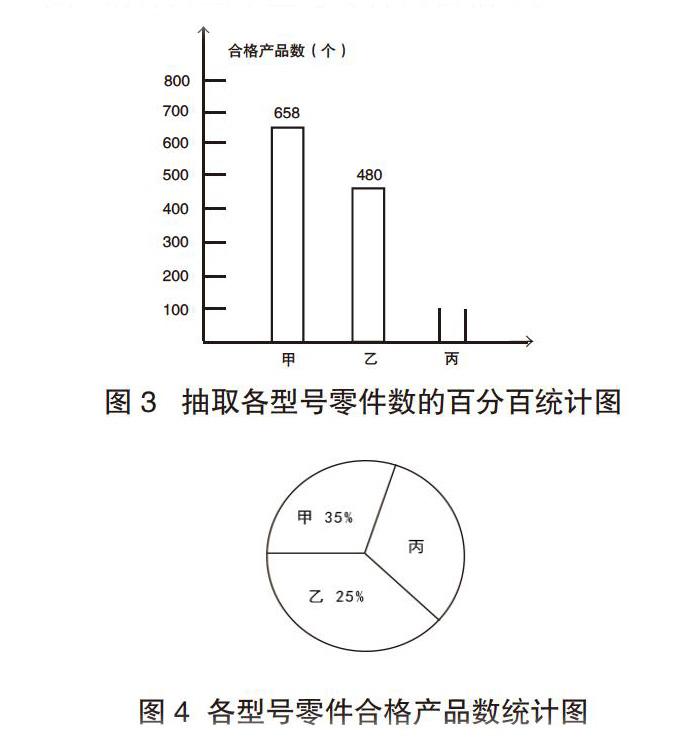
例题:质检部门对甲、乙、丙三种型号的零件及合格产品抽检,随机共抽取了2000个零件,抽到的每种型号零件数量不同。抽检结果显示,丙型号零件合格率为95%。下面是根据质检结果绘制的两幅不完整的统计图(见图3、图4)。
(1)参见抽检的丙型号零件有多少个?(2)计算出丙型号零件合格产品个数,并在条形统计图中补充完整。(3)请计算出甲型号零件的合格率。
题中出现了“抽样总数”“抽样百分率”“合格数量”和“合格百分率”等大量信息,而且有些信息就蕴含在图形中,这给学生理解题意、分析信息增加了难度。一道简单的有关百分率的问题,如单独设计,解题正确率不会低于80%,但是置身于这种问题情境中,学生的正确率降至60%左右。可见,引导学生学会耐心细致、逐条分析信息,汲取问题解决的必要信息,从而正确解题问题,是讲评练习卷时不可忽视的关键点。
1.分析信息—逐条分析,读懂题意
当信息呈现量多、面广、形式多样的情况时,教师在讲评试卷前必须引导学生对信息做梳理与分析。如例题,教师首先可以联系实际分析问题,其次分析“随机共抽取了2000个零件”指的是什么?从“扇形统计图”和“条形统计图”中能得到什么信息等。这是学生正确解题的前提。
2.提取信息—利用标注,明确思路
这类习题另一特点就是隐藏了部分信息,这就需要用标注的方式把不完整的信息清晰地呈现出来。
对于例题中的 (1)(2):出现“2000×95%”或“(2000-856-280)×95%”两种错误。
教师错因诊断:从检测情况看,问题(1),正确率相对高些,原因在于提取有用信息简单,而问题(2),对准确分析信息、提取信息的要求高些,求的是问题(1)的结果的95%是多少?错误率较高。从学生答题情况看,主要是受多余信息的干扰,不能准确提取有用信息。
分析讲解这类题时,教师必须引导学生根据问题寻找、提取必要信息,并在问题旁进行适当的标注,同时也可以记录解题的思路,帮助学生建立解决问题的方法。
3.切换信息—沟通联系,灵活转换
基于丰富的数学信息,教师可以借助题目要求学生深入思考,如“你还能从这些信息中联想到哪些新的数学信息吗”“你还能根据这些信息提出其他的数学问题吗”等,从而实现知识点的切换、思维的发散。
当学生提出“想知道哪种零件抽检数量最多?”这个问题时,教师可以通过“甲∶乙∶丙=35%∶25%∶40%=7∶5∶8”,实现统计、百分数、比信息间的转换。当学生提出“如何知道哪种零件抽检的情况最好,对这个部门进行奖励?”这个问题时,教师就能充分挖掘统计的意义,引导学生用百分数解决统计中的决策问题等。教师只有给学生提供充足的时间、合理的思考方式,才能充分挖掘这类习题的价值,真正沟通知识间的联系,实现信息间的切换。
结 语
综上所述,策略作为解决问题的一种计策,需要学生在解决问题的过程中不断体验,自主反思,也需要教师的引导与概括。因此,教师只有让策略在自然、和谐的氛围中自由呼吸、自我成长,才能促进学生有意义地生成策略,引发学生自主用策略与方法解决问题,从而真正实现数学教学的高质、高效。
[参考文献]
蔡水华.借几何直观 促问题解决[J].教学月刊小学版(数学),2012(10):43-45.
作者简介:王婵丹(1979.1—),女,浙江奉化人,本科学历,一级教师。

