进给系统滚珠轴承热特性分析
李朕均,邵桂阳,张皓轩,李 爽
(1.东北大学机械工程与自动化学院,辽宁沈阳110819;2.东北大学 工程训练中心,辽宁沈阳110819;3.国网吉林省电力有限公司四平供电公司,吉林 四平136000)
随着我国工业技术的快速进步,提高生产率和降低生产成本已经成为科学研究的重点,高速机械加工(HSM)已经成为工业生产中的关键技术。角接触球轴承作为滚珠丝杠进给系统的关键部件,对其热性能进行预测分析是保证机床工作精度的关键。轴承部件作为高速数控机床进给系统重要组成部分,其工作温度对轴承系统性能影响巨大[1-3]。Lin等[4]研究了轴承预紧力对轴承刚度的影响,分析高速旋转效应下离心力和陀螺力矩对主轴的影响。徐敏、江淑云等[5]基于有限元方法对机床主轴系统进行温度分析,考虑接触热阻和热功率随着温度变化带来的影响。以上研究表明,深入研究滚珠轴承的热特性,预测轴承温度场具有深远意义。
1 轴承系统的热源发热率计算
1.1 准静态模型
轴承在高速运行时,滚动体的动力载荷,即离心力及陀螺力矩与热引起轴承部件不均匀膨胀有关的附加载荷,将改变作用在滚珠与滚道接触区的载荷分布。当在高速运转状态下,热导致的预载荷变化对轴承动力学特性影响达到显著水平,影响轴承部件的发热率和热传导。
本文研究对象Z轴进给系统轴承为NSK公司的25TAC62B滚珠丝杠专用轴承如图1所示,轴向预紧力为1 000 N。如表1所示为轴承尺寸和材料参数。

图1 轴承模型

表1 轴承参数和材料属性
如图2描述了角接触球轴承滚动体中心与槽曲率之间的关系。当轴承高速运转时,陀螺力矩和离心力作用下,滚珠中心、轴承内圈曲率中心、轴承外圈曲率中心不再共线。球与槽曲率中心的关系由勾股定理可表示为。

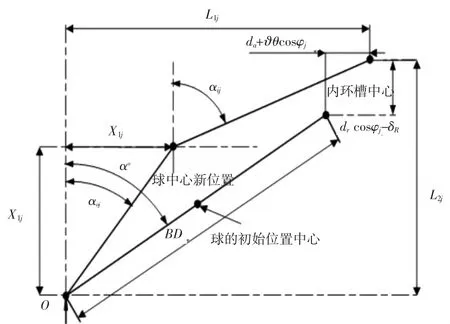
图2 滚动体中心和滚道曲率中心的位置变化
其中,L1j和L2j是分别内外环槽曲率中心之间的轴向距离和径向距离,fo和fi分别为轴承内、外的沟道曲率,ϑ为内沟道曲率中心轨迹半径,θ为内、外圈的相对角位移,da和dr分别为内圈中心的相对轴向和径向位移。
αi和αo被定义正如从图1中看到。

考虑了离心力Fcj和陀螺力矩Mgj,角接触球轴承中滚珠的方位角和载荷如图3所示。根据图3建立水平和垂直方向的力平衡方程,如式(7)所示。


图3 滚动体所受载荷位置
Qij和Qoj与法向接触变形的关系如下式表示

上述离心力和陀螺计算如下:
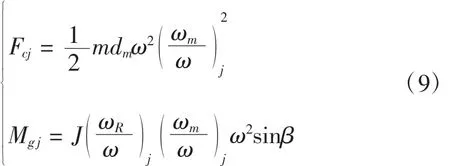
这里m是滚珠重量,J是滚珠转动惯量,dm轴承节圆直径,ωR为滚珠的自转角速度,ωm为滚珠的公转角速度。
为了求解 X1j、X2j、δoj、δij、参数,需要建立整个轴承的平衡方程如下:

式中,Fa和Fr分别代表轴向和径向载荷,Z是球的编号。求解时使用Newton-Raphson方法重复计算直到满足精度输出结果。
1.2 发热率计算
轴承的发热率与轴承参数、润滑油运动粘度、预紧力和转速有明显的关系。轴承的发热率是引起轴承温度场的源头,球轴承的整个摩擦热计算公式被Harris 给出[6]。

其中n是轴的转速,M是滚珠轴承的总摩擦力矩。
摩擦力矩M是由两部分组成:

与载荷有关的摩擦力矩M1为可按如下方式计算:

其中,f1为与轴承类型和所受负荷有关的系数;P1为确定轴承负荷;dm为轴承节圆。
M2为粘性摩擦力矩:
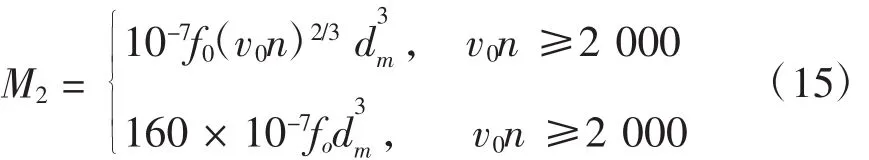
其中,f0为与轴承类型和润滑方式有关的系数;v0为工作温度下润滑剂的运动粘度。
根据沟道控制理论,当接触载荷是动态时,球体与内滚道之间的自旋摩擦力矩。
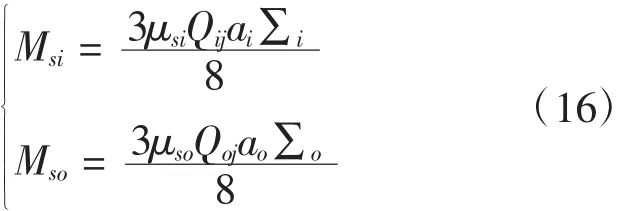
其中,μsi和 μso分别表示摩擦系数。∑i和∑o是第二类椭圆积分。Qij和Qoj在上一节1.1中求解。
1.3 换热系数计算
在有限元模型中需要完整定义结构的热传递系数,由于数控机床通常工作在恒温车间,本文在研究进给系统的热特性不考虑辐射和环境变化的影响。因此主要的散热方式为轴承系统与空气的强制对流换热,通过公式计算。

其中,Nu为努塞尔系数;ld为滚珠丝杠的直径;λfluid为空气的导热系数;Re为雷诺数;Pr为普朗特数;uf为空气的运动粘度;vfluid是空气的动力黏度;Cfluid为空气的比热容。
2 轴承温度场有限元分析
根据上一节中计算方法准确计算发热率,计算完成后,进行Ansys仿真计算来实现预测轴承系统的温度分布。见图4。
图4 轴承系统有限元模型
研究滚珠轴承的温度场必须对有限元模型做出如下假设:
(1)不考虑润滑和热辐射对热传导的影响;
(2)忽略进给系统中的倒角和圆角等细节;
(3)对流换热系数相对固定值。
使用ANSYS软件建立其有限元模型,选择PLANE55单元,经过处理后的有限元模型如图4所示,同时需要设置三种热边界条件,即设置边界的温度值,热流密度值、边界上物体与周围的表面换热系数。
3 结果分析
本文研究对象为数控机床进给系统Z轴成对安装的轴承。基于本文计算的发热率和建立的有限元模型进行计算分析,图5显示了在1 000 r/min空载工作1 h工况下的轴承部件瞬态温度场。研究发现球的温度比内滚道和外滚道温度高得多。产生的大量热量通过轴承元件向外散热,摩擦生热导致轴承元件温度发生较大变化。

图5 轴承系统温度分布
图6 显示了随时间变化的轴承不同位置的温度变化曲线,可以看出随着时间的推移轴承各节点温度随时间推移呈指数上升,更多的摩擦热在整个轴承座和轴上消散,并且球和内外圈之间的温差逐渐变小,可以推测当轴承摩擦热源产生的热量和散发的热量达到平衡时,温度场接近稳态达到热平衡趋于稳定。热平衡分析表明了温度场分析结果的可靠性和准确性。

图6 典型温度节点的瞬态温升曲线
4 结论
本文建立了机床进给系统热源和温度场计算方法,实现精确计算轴承发热率并预测轴承内部温度分布。采用轴承系统结合连接部件的整体有限元分析,利用Anays软件对轴承系统进行仿真,满足进给系统工程要求,实现预测轴承内部温度场特性分布规律及随时间的变化趋势,更好地预测轴承温升。对进给系统滚珠轴承的热分析提供了一种精确可行的计算方法。

