D-S证据理论改进算法对比研究

徐孙庆

（92493部队60分队，葫芦岛 125000）

0 引言

证据理论最早是由美国的数学教授Dempster A P于1967年提出来的，在他研究多值映射问题时，最早给出了上限概率以及下限概率的定义[1]。Shafer[2]对这一理论进行了深入的拓展研究，并将基本概率分配函数引进进一步发展，形成了一套完整的理论体系。1981年，人工智能专家Barnett[3]将这一理论正式引进了人工智能领域，并建议将这一理论定名为DS证据理论，此后证据理论迅速发展，在各领域的研究开花结果，文献成果众多，并且已经广泛的应用于图像处理、模式识别、故障诊断、风险评估、技术状态评估等相关领域。

尽管目前的研究如火如荼的展开着，但仍存在一些问题亟需解决。特别是对冲突证据进行合成时，D-S证据理论并不能很好地对其进行合成，甚至会产生反直觉的结果。Zadeh[4]最早发文指出，这种情况是由于合成规则的固有不足造成的。查阅相关的文献可知，目前大多数文献对冲突证据融合的研究成果、改进方法主要可以归纳为两个方面：一方面是对合成规则进行改进。在这类方法中，较为经典的是Yager[5]提出的将冲突分配给空集。另一方面是在证据融合前对证据进行预处理，修改证据源模型。Murphy[6]提出的修改模型是较为经典的加权平均法，通过对证据进行简单的加权处理进而达到改善冲突证据融合结果精确性的目的。

不同方法有着不同的优缺点。有些方法可能对高冲突证据的融合效果较好，但对差异性较小的证据的合成可能效果不好；有些方法可能会有较快的收敛速度和较高的可靠性，但可能公式更复杂，计算量更大。目前没有一个解决方法能够被广泛的接受。因此，本文主要对冲突证据合成的研究现状进行了介绍，对两种典型的改进算法进行对比研究，并运用算例对不同方法的合成效果进行了验证。本文的结论能够为后续改进算法研究提供借鉴。

1 D-S证据理论及其不足

本节主要介绍证据理论的基本概念，以及在处理证据冲突时存在的不足。

1.1 基本概念

定义1-1：假设在识别框架中，若集函数m：2Θ→[0，1]表示从集合2Θ映射到区间[0，1]（2Θ为Θ的幂集），并且满足以下条件：

则称m为识别框架Θ上的基本信任分配函数。

定义 1-2：假设在识别框架 Θ 中，m：2Θ→[0，1]是识别框架Θ上的基本信任分配函数，则由公式（3）定义的函数Bel：2Θ→[0，1]称作识别框架Θ上的信度函数.

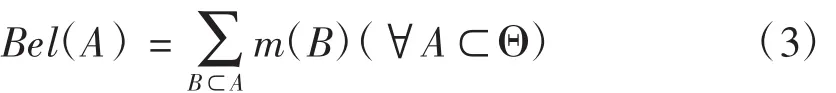
假设E1，E2分别是识别框架下的两个证据，Bel1，Bel2是同一识别框架上的两个信任函数，m1、m2分别是两个证据所对应的基本信任分配函数，焦元分别为 A1，…，Ak和 B1，…，Bj，若：

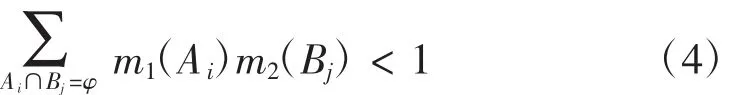
那么D-S证据理论的合成规则为：

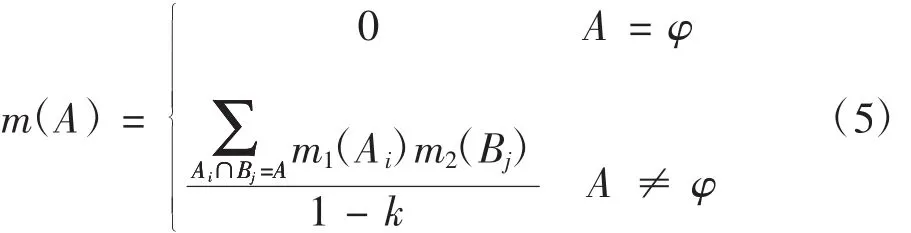
1.2 D-S证据理论存在的不足

证据间的差异性较小时，Dempster合成规则能够较好地对证据进行合成，以较高的信度得到目标命题。但是当证据间的差异性较大甚至完全对立、冲突时，则无法很好地合成证据，甚至无法对证据进行合成。

算例1：全冲突悖论的计算

假设存在某一识别框架为Θ＝{A，B}，给定两个证据E1，E2，对应的焦元分别是 A，B，相应的基本概率分配为：

根据前述介绍，此例中的冲突系数k=1×1+0×0＝1，表明两个证据完全对立，不能利用Dempster合成规则进行合成，D-S证据理论失效。由于DS证据理论在这种情况下将不能使用，不能对证据进行有效的处理。此即为Zadeh悖论，也称为全冲突悖论。D-S证据理论无法解决全冲突悖论问题。

算例2：绝对信任悖论的计算

假设存在某一识别框架为Θ ＝{A，B，C}，给定两个证据E1，E2，对应的焦元分别是A，B，C相应的基本概率分配为：

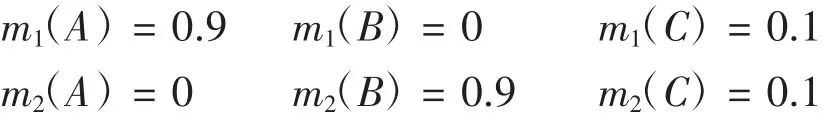
利用Dempster合成规则，冲突系数k＝0.09+0.81+0.09=0.99。证据E1，E2高度冲突。两个证据分别以0.9的信度分别支持命题A和命题B。

利用合成规则进行计算有：

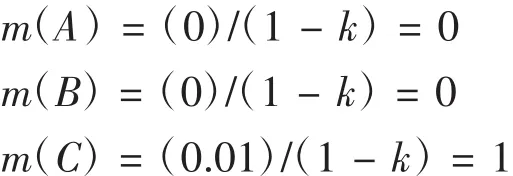
两个证据合成的结果显示为支持命题C的概率值为1，这个结果是与常理相悖的，说明证据合成失效，D-S证据理论也不能用于处理此类问题。

2 典型的两类改进方法

D-S证据理论经过几十年的发展在各领域开花结果，但是对冲突证据的合成仍然没有一个很好的解决方法。为了解决冲突证据的合成，已经有很多研究给了一些方法。目前对D-S证据理论的改进主要有两个思路：一个是从证据源模型进行改进，其代表方法是Yager法；另一个是从合成规则进行改进，其代表方法是Murphy法。

2.1 Yager法

Yager认为证据融合失效时由于组合规则的不足引起的，因此假设识别框架是封闭的，将冲突部分全部分配给未知，其组合公式如下：

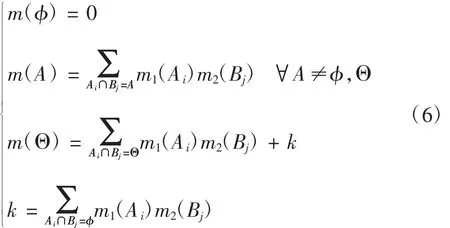
2.2 Murphy法

Murphy提出改进原始证据的方法以弥补D-S证据组合规则的不足。首先求出所有证据的基本概率分配值的算术平均，然后利用经典的D-S组合规则进行n-1次融合。该方法的计算过程如下：

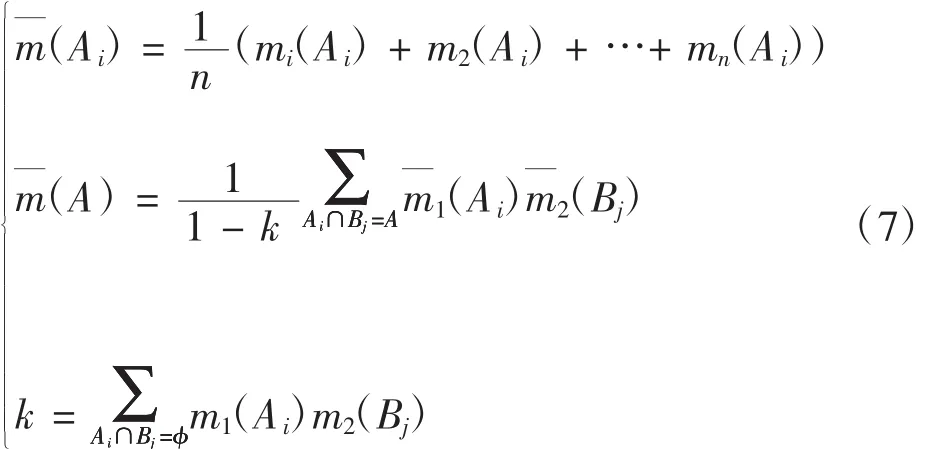
3 算例验证

本节主要通过几个算例来对比不同改进方法的优劣。

算例3假设识别框架为Θ ={A，B，C}，各证据的基本概率赋值为：

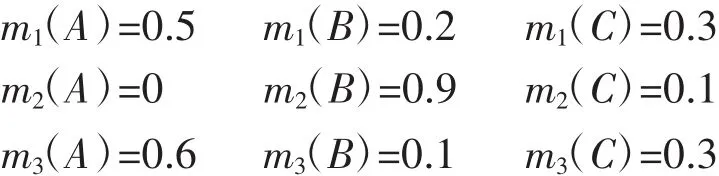
根据计算，各算法的合成结果如表1、表2所示。

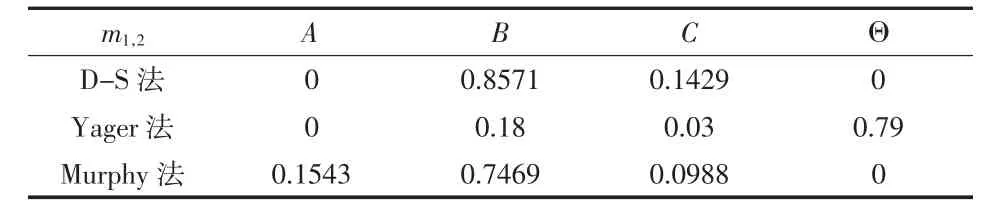
表1 两个证据的合成结果

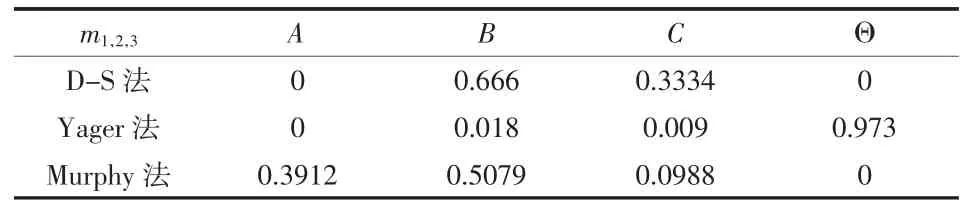
表2 三个证据的合成结果

由表1和表2可以看出，D-S证据理论对高冲突的证据无法很好地进行合成。由于m2（A）=0，导致命题A被完全否定，即使后续有更多的证据支持命题A，合成结果永远显示命题A的支持度为0。Yager方法也不能很好地解决冲突证据的合成问题，其合成结果过于保守，命题的不确定性增强，特别是在证据数量较多时，无法很好地为决策服务。Murphy法对证据进行简单的算术平均，没有考虑各证据间的权重及冲突，但是其合成效果较前两种方法好。算例结果表示Murphy能够较好地解决冲突证据的合成问题，结论也更加科学合理。

4 结束语

通过算例的对比计算可知，相较于改进合成规则这一方法，对证据体本身的改进更为有效。对合成规则的改进破坏了可交换原则且容易丧失其良好的数学特性。实际上，如果是由于证据不可靠造成的证据冲突，那么这种情况下对合成规则进行改进也是没有意义的。因此，为了更好地解决证据冲突问题，需要在证据合成前对证据进行预处理，这样能使合成结果更为科学准确。然而，由于证据冲突的客观存在，目前仍没有一个统一的被广泛接纳的解决方法，需要进一步加以研究。