非线性能量阱在悬臂薄板振动抑制中的应用研究

刘艮 张伟

摘要： 悬臂结构在航空航天领域应用广泛，由于结构受到激励作用而产生共振行为，因此结构的振动抑制问题显得尤为重要。非线性能量阱（Nonlinear Energy Sink，NES）以质轻、能量单向传递以及减振效率高等特点，为其引入到航空航天结构的减振设计中提供了条件。利用NES对悬臂矩形板进行减振研究。考虑Kirchhoff经典薄板模型，建立了薄板与NES耦合的动力学方程，通过模态截断研究了薄板一阶横向弯曲时结构的响应问题，分析了不同参数下NES的减振效果，发现NES对结构响应位置较为敏感，并且在位移响应最大位置处减振效果最大。以期为悬臂结构在工程应用中提供一些理论上的支持。

关键词： 非线性能量阱; 振动抑制; 悬臂薄板; 瞬态响应

中图分类号： O322; TB535  文献标志码： A  文章编号： 1004-4523（2019）05-0786-07

DOI：10.16385/j.cnki.issn.1004-4523.2019.05.006

引 言

悬臂结构在航空航天工程领域的研究中应用广泛，新型飞行器的翼面，压气机的叶片及航天工程中的机械臂、人造卫星的太阳翼等都是典型的悬臂构件。由于这些结构的工作环境复杂，在各种载荷作用下容易引起结构的振动，从而影响到整体系统的性能[1-3]，必要的减振手段是值得考虑的。

随着结构工作环境的复杂化，传统的减振手段已经不能较好地满足工程需要。非线性能量阱与传统减振器相比以其附加质量小、抑制频带宽、能量靶向传递等特点，逐渐成为结构减振研究中所关注的热点。对离散系统及线性连续系统附加非线性能量阱进行靶向能量传递的研究始于2000年初。Gendelman[4]在研究两自由度线性振子耦合一个含有三次非线性刚度及阻尼元件附件的瞬态动力学问题中首次实现了能量的靶向传递。在早期的研究中，学者们将含有三次非线性刚度的元件附加于不同的离散结构中，形成耦合系统，利用非线性能量阱实现结构的宽频被动减振。

随后，文献[5-10]将NES对结构的减振研究从离散系统拓宽到连续系统，从简单的有限自由度的线性弹簧质量系统推广到了连续介质的梁板结构中，不仅从理论分析了非线性能量阱的减振效果，而且从实验方面得到了有力的验证，为NES在结构减振方面的应用奠定了基础。

近年来，应用NES对结构进行振动抑制的研究方兴未艾，Zhang等[11-12]将NES的被动振动抑制应用到了轴向运动梁的减振研究中，考虑轴向运动梁在瞬态激励作用下，附加单个NES以及附加一对平行布置的NES的减振效果。Kani等[13]将NES的减振问题应用到了非线性简支梁的振动抑制中，将传统的线性结构的减振向非线性结构减振迈进。悬臂结构在旋转部件中应用广泛，Bab等[14]利用NES對旋转梁结构进行了减振研究。

在实验分析方面，Kremer等[15]通过实验与理论相结合的研究方法，分析了非线性能量阱作为吸振器的能量传递方式。同时，中国的学者也在应用NES进行结构减振的研究中做出了贡献。Chen等[16-17]研究了以桁架为核心的梁结构的振动抑制问题，并对成对布置的NES附件简支梁的高分支响应问题进行了分析。文献[18-19]对含有一类立方非线性刚度的吸振器的能量传递及参数设计进行了研究。陈等[20]对串联和并联NES的吸振效能进行了对比研究，分析了不同参数对吸振效能的影响。

本文以悬臂矩形薄板为研究对象，针对NES对悬臂板结构的瞬态激励下的振动抑制问题进行研究。通过模态截断的方法考虑悬臂板振动的低阶模态振型的情况，分析NES在不同放置位置及不同系统参数时对减振效果的影响，以期为悬臂薄板结构的减振设计提供理论上的支持。

1 理论模型

悬臂薄板由于结构尺寸上的特殊性，在结构受到横向扰动时，容易发生横向弯曲振动，所以本文对薄板在横向振动时的动力学方程进行建模。

将含有三次非线性刚度的NES附件附加到矩形薄板的结构中，考虑悬臂边界形式，矩形薄板一边固定，其他三边自由，如图1所示。

4 TMD和NES减振效果对比

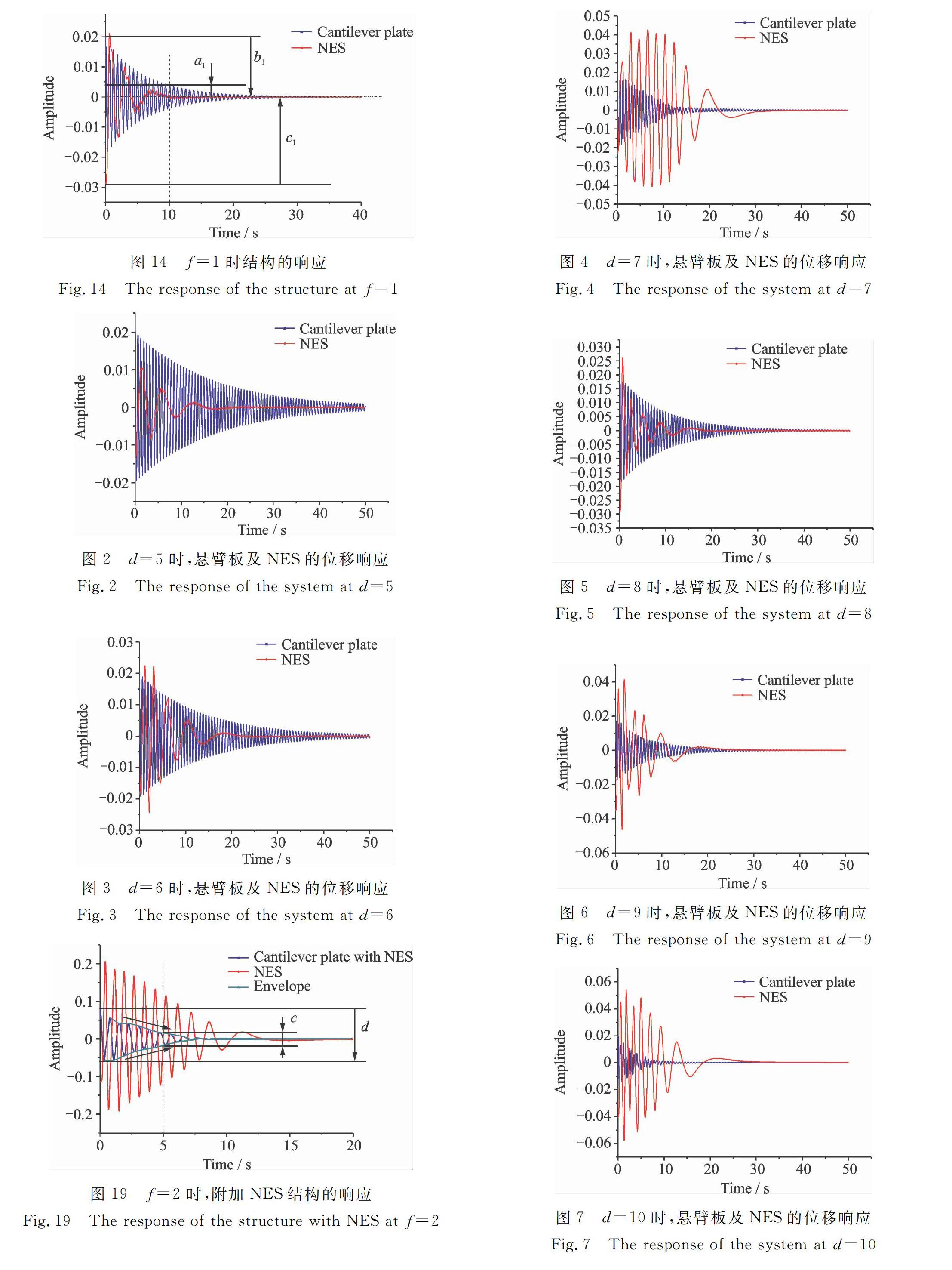
相比于线性刚度阻尼减振器（TMD），NES被动减振效果优势明显。图18和19选取了激励位于自由端，激励幅值f=2，线性阻尼减振器及NES附件布置于d=9时，结构的响应衰减情况。由于非线性系统的耦合作用，附加NES的悬臂结构的初始响应较线性减振器耦合结构大，但是附加NES结构的衰减效果明显，比较图18中a，b附加线性刚度阻尼减振结构的初始及一段时间后的衰减幅值以及图19中c，d附加NES结构的衰减幅值，明显地，在附加NES的结构中，在激励发生后的5 s左右时，结构振幅的衰减就达到了可观的程度，振幅下降的趋势更为陡峭，体现了NES的良好的减振效果。

5 结 论

本文研究了悬臂薄板结构附加NES附件的瞬态振幅抑制问题。基于Kirchhoff假设建立了薄板与NES耦合的动力学方程，通过模态截断研究了薄板一阶横向弯曲时，结构的响应问题，分析了不同参数下NES的减振效果。通过选取NES不同布置位置，研究了NES挂载位置对振动衰减的影响。对比了NES在不同位置时，悬臂薄板在一定时间内振幅衰减效果。与线性刚度质量阻尼减振附件的振幅抑制效果进了对比，可以看到NES在瞬态激励下有着较高的振幅抑制效率，优势明显。通过以上研究，以期为NES投入到工程结构的减振应用中提供理论上的支持。

参考文献：

[1] 吕书锋， 张 伟. 复合材料悬臂外伸板的非线性动力学建模及数值研究[J]. 动力学与控制学报， 2015， 13（4）： 288-292.

Lü Shufeng， Zhang Wei. Nonlinear analysis of deploying laminated composite cantilever plates[J]. Journal of Dynamics and Control， 2015，13（4）： 288-292.

[2] 楊佳慧， 张 伟， 姚明辉. 受电压激励的复合材料悬臂板的分叉分析[J]. 动力学与控制学报， 2017， 15（6）： 489-493.

Yang Jiahui， Zhang Wei， Yao Minghui. Bifurcations of a composite laminated cantilevered plate under voltage excitation[J]. Journal of Dynamics and Control， 2017， 15（6）： 489-493.

[3] 王 宇， 郝育新. 含几何缺陷的均质材料悬臂薄板的自由振动[J]. 动力学与控制学报， 2017， 15（6）： 525-531.

Wang Yu， Hao Yuxin. Free vibration of homogeneous cantilever thin plate with geometric imperfection[J]. Journal of Dynamics and Control， 2017， 15（6）： 525-531.

[4] Gendelman O V. Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators[J]. Nonlinear Dynamics， 2001， 25（1-3）： 237-253.

[5] Gendelman O， Manevitch L I， Vakakis A F， et al. Energy pumping in nonlinear mechanical oscillators： Part I—Dynamics of the underlying Hamiltonian systems[J]. Journal of Applied Mechanics， 2001， 68（1）： 34-41.

[6] Vakakis A F， Gendelman O. Energy pumping in nonlinear mechanical oscillators： Part II—Resonance capture[J]. Journal of Applied Mechanics， 2001， 68（1）： 42-48.

[7] Vakakis A F. Inducing passive nonlinear energy sinks in vibrating systems[J]. Journal of Vibration and Acoustics， 2001， 123（3）： 324-332.

[8] Gendelman O， Manevitch L I， Vakakis A F， et al. A degenerate bifurcation structure in the dynamics of coupled oscillators with essential stiffness nonlinearities[J]. Nonlinear Dynamics， 2003， 33（1）： 1-10.

[9] Vakakis A F， Rand R H. Non-linear dynamics of a system of coupled oscillators with essential stiffness non-linearities[J]. International Journal of Non-Linear Mechanics， 2004， 7（39）： 1079-1091.

[10] Musienko A I， Lamarque C H， Manevitch L I. Design of mechanical energy pumping devices[J]. Journal of Vibration and Control， 2006， 12（4）： 355-371.

[11] Zhang Y W， Zhang Z， Chen L Q， et al. Impulse-induced vibration suppression of an axially moving beam with parallel nonlinear energy sinks[J]. Nonlinear Dynamics， 2015， 82（1-2）： 61-71.

[12] Zhang Y W， Yuan B， Fang B， et al. Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink[J]. Nonlinear Dynamics， 2017， 87（2）： 1159-1167.

[13] Kani M， Khadem S E， Pashaei M H， et al. Vibration control of a nonlinear beam with a nonlinear energy sink[J]. Nonlinear Dynamics， 2016， 83（1-2）： 1-22.

[14] Bab S， Khadem S E， Mahdiabadi M K， et al. Vibration mitigation of a rotating beam under external periodic force using a nonlinear energy sink （NES）[J]. Journal of Vibration and Control， 2017， 23（6）： 1001-1025.

[15] Kremer D， Liu K. A nonlinear energy sink with an energy harvester： Transient responses[J]. Journal of Sound and Vibration， 2014， 333（20）： 4859-4880.

[16] Chen J E， Zhang W， Yao M H， et al. Vibration suppression for truss core sandwich beam based on principle of nonlinear targeted energy transfer[J]. Composite Structures， 2017， 171： 419-428.

[17] Chen J E， He W， Zhang W， et al. Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks[J]. Nonlinear Dynamics， 2018， 91（2）： 885-904.

[18] 張也弛， 孔宪仁， 杨正贤， 等. 非线性吸振器的靶能量传递及参数设计[J]. 振动工程学报， 2011， 24（2）： 111-117.

Zhang Yechi， Kong Xianren， Yang Zhengxian， et al. Targeted energy transfer and parameter design of a nonlinear vibration absorber[J]. Journal of Vibration Engineering， 2011， 24（2）： 111-117.

[19] 熊 怀， 孔宪仁， 刘 源. 一类立方非线性吸振器的能量传递和耗散研究及参数设计[J]. 振动工程学报， 2015， 28（5）： 785-792.

Xiong Huai， Kong Xianren， Liu Yuan. Energy transfer and dissipation of a class of nonlinear absorber and its parameter design[J]. Journal of Vibration Engineering， 2015， 28（5）： 785-792.

[20] 陈建恩， 何 伟， 葛为民. 并联非线性能量阱吸振效能仿真研究[J]. 系统仿真学报， 2018， 30（9）： 3411-3419.

Chen Jianen， He Wei， Ge Weimin. Simulation study on vibration absorption efficiency of parallel nonlinear energy sinks[J]. Journal of System Simulation， 2018， 30（9）： 3411-3419.

[21] 刘延柱， 陈立群， 陈文良. 振动力学[M]. 第2版. 北京：高等教育出版社，2011： 183-188.

Abstract： Cantilever structures are widely used in the field of aerospace engineering. It is very important to restrain the vibration of these structures because of their resonance behavior under external excitation. The Nonlinear Energy Sink （NES）， which is characterized by light weight， targeted energy transfer and high damping efficiency， can be used in the design of vibration suppression of aerospace structures. In this paper， the vibration reduction of cantilever rectangular plates using the NES is studied. Considering the classic Kirchhoff plate model， the dynamic equation of the thin plate coupled with the NES is established， and the response of the structure in the first order transverse bending is studied by modal truncation. The damping effect of the NES under different parameters is analyzed. It is found that the NES is sensitive to the response position of the structure and has the maximum effect of vibration reduction at the position with the maximum displacement response， which can provide some theoretical support for the cantilever structure in engineering application. 

Key words： nonlinear energy sink; vibration suppression; cantilever thin plate; transient response

作者简介： 刘 艮（1991-），女，博士研究生。电话：18810946395;E-mail： liugen1991@hotmail.com

通讯作者： 张 伟（1960-），男，教授。电话：（010）67392867;E-mail： sandyzhang0@yahoo.com