基于改进纹理特征的现堪图像检索算法

兰 蓉, 马 威

(1.西安邮电大学 通信与信息工程学院， 陕西 西安 710121；2.电子信息现场勘验应用技术公安部重点实验室， 陕西 西安 710121；3.陕西省无线通信与信息处理技术国际合作研究中心， 陕西 西安 710121)

纹理作为一种重要的视觉线索，广泛存在于自然界各种物体的表面，在图像中则体现为特征值强度的某种局部重复模式的宏观表现[1]。近年来基于纹理特征的图像检索得到了广泛研究，其方法归纳起来主要有统计法、模型法、信号处理法及结构法等[2]。统计法[3]主要是用像素及邻域像素的灰度信息来研究图像的纹理特性，灰度共生矩阵(gray-level co-occurrence matrix, GLCM)具有较强的适应性与鲁棒性，且方法简单，在统计分析领域应用较广；信号处理法[4]主要是建立在频域、时域以及多尺度的基础上的信号分析方法，其中小波变换具有在时间、频率上突出信号局部特征的能力，并且可以对图像的纹理进行多分辨表示，更加符合人类的视觉特征，因此其在信号处理领域中应用较广泛。

现堪图像[5]源于真实的案发现场，其局部纹理信息比较丰富且边缘特殊，如指纹类的局部纹理基本呈椭圆形分布；轮胎类的局部纹理呈边块形、线条形分布；鞋印类的局部纹理多数成边块形、交织形、点状、圆形、波折或线条形分布；墙类的局部纹理呈边块形、线条形分布等。在现堪图像的纹理特征提取中，文献[6]使用灰度共生矩阵对现堪图像纹理特征进行描述，但灰度共生矩阵仅对单个像素点与邻近像素点的概率统计，缺少对图像整体空间分布的描述，难以精确表示像素间的依赖关系，因此该方法的检索效果并不理想。文献[7]利用双树复小波变换(dual- tree complex wavelet transform, DT-CWT)结合灰度共生矩阵对图像的纹理特征进行描述，但双树复小波变换对图像局部结构细节敏感，当图像不是规则图像或图像某一局部区域像素值不相似时，该纹理提取算法会使得检索算法的效果不佳。文献[8]使用改进双树复小波结合灰度-梯度共生矩阵对图像纹理特征进行描述，该算法对图像进行非均匀分块，当图像纹理分布不明显、不均匀以及图像包含大块的平滑区域时，灰度-梯度共生矩阵则不能有效反映图像的纹理信息，进而影响检索算法的检索准确率。

针对灰度共生矩阵缺少图像纹理的整体空间分布特征与双树复小波变换对图像结构细节敏感的缺陷，本文提出一种基于改进纹理特征的现堪图像检索算法。首先，利用灰度共生矩阵与双树复小波变换提取图像的纹理信息；其次，利用均匀分块，以各个块角点的疏密程度来对图像的空间分布特性进行描述，以各个块的灰度差分统计来增强图像纹理细节信息描述；然后，对纹理信息融合图像的空间分布特性和结构细节信息，完成现堪图像的纹理特征提取；最后将提取的纹理特征应用于现堪图像检索。以期能更全面的描述图像的纹理特征，提高现堪图像检索算法的检索准确率。

1 纹理信息

图像的纹理是图像的基本特征信息，这部分将利用双数复小波变换与灰度共生矩阵对图像的纹理特征进行描述。

1.1 双树复小波变换

提取图像的纹理特征时，考虑到离散小波变换存在平移敏感性和方向选择不充分的问题，所以，采用Kingsbury N. G.提出的双树复小波变换[9]提取图像的纹理特征，该描述符能改善离散小波变换的平移敏感性和方向选择不充分的两个缺陷。

一维DT-CWT用两个小波函数表示如下

ψ(t)=ψr(t)+jψj(t)，

其中，小波函数ψr(t)为DT-CWT的实部，ψj(t)为DT-CWT的虚部。以此构造的双树复小波函数具有可解析性，实现图像重构。

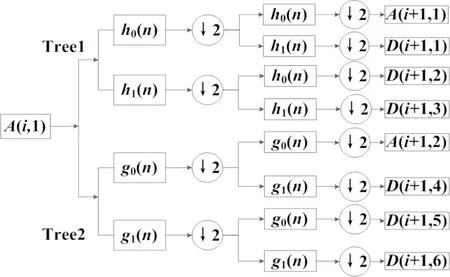
图1 二维DT-CWT的分解过程

图1是二维DT-CWT的分解过程。二维DT-CWT采用滤波器ho(n)、h1(n)、g0(n)、g1(n)等分别对输入的二维信号交替进行列间的变换，可分解出2个低频子带以及6个方向(-75°,-45°,-15°,15°,45°,75°)的高频子带[10]。DT-CWT将小波变换的空间信息延伸到复数域，能够实现对纹理多方位分布信息的提取。因此，使用DT-CWT可以更为具体地从多方向分析图像的纹理特征

1.2 灰度共生矩阵

灰度共生矩阵是一种反映具有同样亮度或接近亮度的像素之间的位置分布特性二阶统计量，它通过生成相关矩阵来描述图像的纹理特征[11]，适用性强，鲁棒性高，因此，本文采用灰度共生矩阵对图像灰度的空间依赖关系进行描述。

设一幅灰度级数为L的图像，在像素点(x,y)处的灰度值为I(x,y)，在θ方向上统计距离为d且灰度值分别为I(x1,y1)=i，I(x2,y2)=j的两个像素点出现频率pij(d,θ)组成的相关矩阵，即为灰度共生矩阵

P=[pij(d,θ)]。

(1)

实验所用图像均来自真实的案发现场，格式为RGB图像，下面介绍利用灰度共生矩阵原理提取图像纹理特征的步骤。

步骤I 将图像转换为灰度图像，对图像进行灰度级压缩，将其均匀量化为16级，即L=16。

步骤II 确定邻近像素间的距离d与角度θ，并提取对应的灰度共生矩阵。为了能够更具体地描述图像纹理的分布特征[7]，本文提取距离d=1，θ分别取0° 、45°、90°、135°时所对应的灰度共生矩阵。

步骤III 在灰度共生矩阵的基础上，计算可描述图像纹理特征的6个纹理参数，分别为能量Easm、熵Hent、惯性矩Qcon、逆差矩Qidm、相关指数Ccor，变换频率的方差Vvar，对应计算公式分别为

(2)

(3)

(4)

(5)

(6)

(7)

式中

2 图像空间分布与结构细节

图像的空间分布信息和结构细节信息是图像纹理分布的重要特征，本部分通过将图像均匀分块，然后将各个块的空间离散度与纹理细节级联起来表征图像整体的空间分布特征与图像结构细节特征。

2.1 图像区域划分

在描述图像的空间结构特征时，首先将图像预处理，将图像统一规范为大小255×255的规格，使得行、列均能被3整除。然后再将图像均匀分成9块，如图2(a)所示，并按照图2(b)的方式进行块间级联。

(a) 图像结构区域划分

2.2 图像空间分布特征

利用角点检测原理提取出整幅图像的角点位置，然后分别计算图像各个区域块的角点疏密度，最后将各个块的角点疏密度按顺序级联，作为整幅图像的空间分布特征。

2.2.1 角点检测

角点是指图像的某点特征在多个方向都发生很大变化的一类特征点。在图像处理中，常通过引入图像角点来描述图像的空间分布特性。Harris角点检测器[12]采用微分运算和自相关矩阵来检测图像角点，因为其运算简单，且提取的角点均匀合理，性能稳定[13]，所以本文选用Harris角点检测器提取图像角点。Harris角点检测的核心思想是建立一个模板窗口在图像上滑动，在垂直与水平方向上都产生较大变化的点就是角点[14]，则自相关函数为

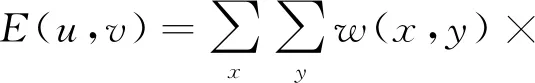
(8)

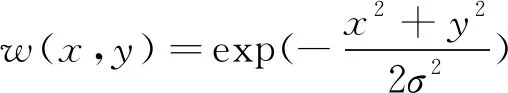
D(u,v)=I(x+u,y+u)-I(x,y)，

将D(u,v)在(0,0)处采用泰勒级数展开，得

其中高阶无穷小忽略不计，则上式可以化简为

因此式(8)可以化简为

(9)

其中

然后，由式(9)定义矩阵M为

建立角点响应函数R为

R=detM-k(trM)2,

式中k是常量，用于调节函数的形状，其取值范围一般为0.04～0.06，本文中k取0.05。当角点响应函数R处于局部极大值时所对应的像素坐标，就是所提取的角点位置。

2.2.2 空间离散度

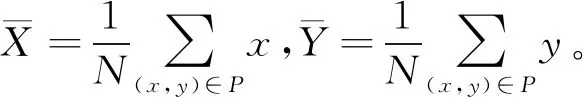
(10)

2.3 图像结构细节信息

采用灰度差分算子计算各个块的纹理粗糙度，以此作为图像各个块的纹理细节特征。设图像第k块中点(x,y)的像素值为I(x,y)，则该块内相邻两点间的灰度差值为

IΔ(x,y)=I(x,y)-I(x+1,y+1)。

假设该区域的灰度级为m,并且IΔ(x,y)出现的概率为pΔ(i)，则该区域的细节特征可以通过计算如下4个纹理参数表示[16]，分别为均值mmean、惯性矩qcon、二阶矩aasm、熵hent，计算公式分别为

(11)

(12)

(13)

(14)

3 改进纹理特征的提取算法

根据上述对图像的纹理特征融合图像的空间分布特性与结构细节特性的表述方法，提出一种改进的纹理特征提取算法。下面将给出算法的具体步骤。

步骤I 将图像都转换为灰度图像，并规范为大小为255×255统一尺寸，使图像水平和竖直方向均能被3整除。

步骤II 提取图像纹理特征。利用双树复小波变换，分别提取图像2个低频子带系数，及-75°、-45°、-15°、15°、45°、75°方向的图像高频子带系数，得到38个特征值；再利用式(1)提取图像的灰度共生矩阵，并利用公式(2)-(7)计算分别在0°、45°、90°、135°方向上的6个纹理参数特征，得到24个特征值。这样就得到描述图像纹理特征的62个参数值。

步骤III 图像空间分布特征与结构细节特征的提取。根据公式(10)计算图像的空间分布特性对应的9个特征值；再根据公式(11)-(14)计算得到36个描述图像细节的特征值。这样，得到45个特征值，即图像的空间分布特征与结构细节特征。

步骤IV 将步骤II与步骤III提取的特征级联，将它们作为图像的纹理特征，共107个特征值，完成现堪图像的纹理特征提取。

4 基于改进纹理特征的图像检索算法

设计相应的检索算法，通过检索算法的评价指标衡量所提算法的纹理判别能力。下面将给出基于改进纹理特征的图像检索算法步骤。

步骤I 根据本文算法分别对目标图像与数据库图像提取纹理特征。

步骤II 使用街区距离度量目标图像与数据库图像纹理特征的相似性[17]，返回与目标图像相关的图像。

设fp、fq分别表示数据库图像、目标图像利用改进的纹理特征提取算法得到的纹理特征向量

fp=(p1,p2,…,pi,…,pn)，fq=(q1,q2,…,qi,…,qn),

其中，pi表示提取数据库图像特征向量的第i个分量，qi表示提取查询图像特征向量的第i个分量，n为特征向量的个数。因此，可得街区距离D(fp,fq)为

若距离D(fp,fq)越小，则两幅图像越相似。

5 实验与分析

5.1 实验平台

测试实验平台选择的计算机处理器为Intel(R) Core(TM) i5-3230M，内存4G，使用的操作系统为 Windows10 Professional 64位版本，其程序仿真环境为Matlab2014a-64位。

5.2 实验图库

所用的实验图库为现堪图库[5]，该数据库的图像均来自真实案发现场。由于保密性，实验所用的图像与原始图像相比均有所改动。实验选用的现堪图库共8类，每类共有50幅图像，如图3所示。

图3 现堪数据库中各类的示例图像

5.3 检索性能评价指标

检索算法的性能评价指标选用通常的准确率P和检索率R，其中准确率是指经过目标图像查询后，返回的相关图像数与返回图像总数之比；检索率是指返回的相关图像数与数据库中相关图像总数之比[18]。因此本文通过准确率曲线及P-R曲线(准确率对检索率曲线)检验算法性能。

设检索返回图像数为Nretum，当选定一个图像Q，经过检索，发现返回的这Nretum幅图像中有Na幅图像是相关的，整个图库中与该图像相关的图像总共有Ndata幅，则准确率P与检索率R的表达式分别为

5.3.1 改进纹理特征提取算法的有效性分析

为了客观分析对纹理信息融合空间分布与结构细节特征的有效性，特将基于灰度共生矩阵(gray-level co-occurrence matrix , GLCM)[6]、双树复小波变换结合灰度共生矩阵[7](dual-tree complex wavelet transform and gray-level co-occurrence matrix , DT-GLCM)、改进双数复小波结合灰度-梯度共生矩阵[8](dual-tree complex wavelet transform and gray-gradient co-occurrence matrix, DT-GGCM)和本文算法得到的图像检索结果进行对比，结果如图4～5所示。

图4 4种纹理提取算法的准确率曲线

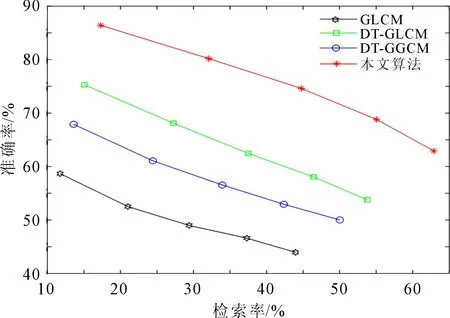
图5 4种纹理提取算法的P-R曲线

从图4可见，当检索返回前10幅图像时，本文算法的平均准确率达到86.425%，当返回前50幅图像时，检索的准确率达到了62.905%，与对比算法中的最优算法相比分别提高了11.125%与9.125%。从图5的P-R曲线分布情况可以看出，本文算法的检索率与准确率均优于这三组对比算法。因此，对利用双树复小波变换结合灰度共生矩阵提取的纹理信息融合图像的空间分布与结构细节特征后，确实能更全面的描述图像的纹理内容，使得算法对现堪图像的纹理描述能力有所提高，进而使得现堪图像检索算法的检索准确率有所提升。

5.3.2 算法对图像的描述性能分析

为检验本文算法对现堪图像的描述性能，特将基于灰度共生矩阵结合颜色特征[6](gray-level co-occurrence matrix and HSV, GLCM-H)、双树复小波变换与灰度共生矩阵结合形状特征[7](dual-tree complex wavelet transform and gray-level co-occurrence matrix and Hu, DT-GLCM-Hu)、改进双数复小波结合灰度-梯度共生矩阵[8](dual-tree complex Wavelet Transform and gray-gradient co-occurrence matrix , DT-GGCM)和本文算法得到的图像检索结果进行对比，结果如图6-7所示。

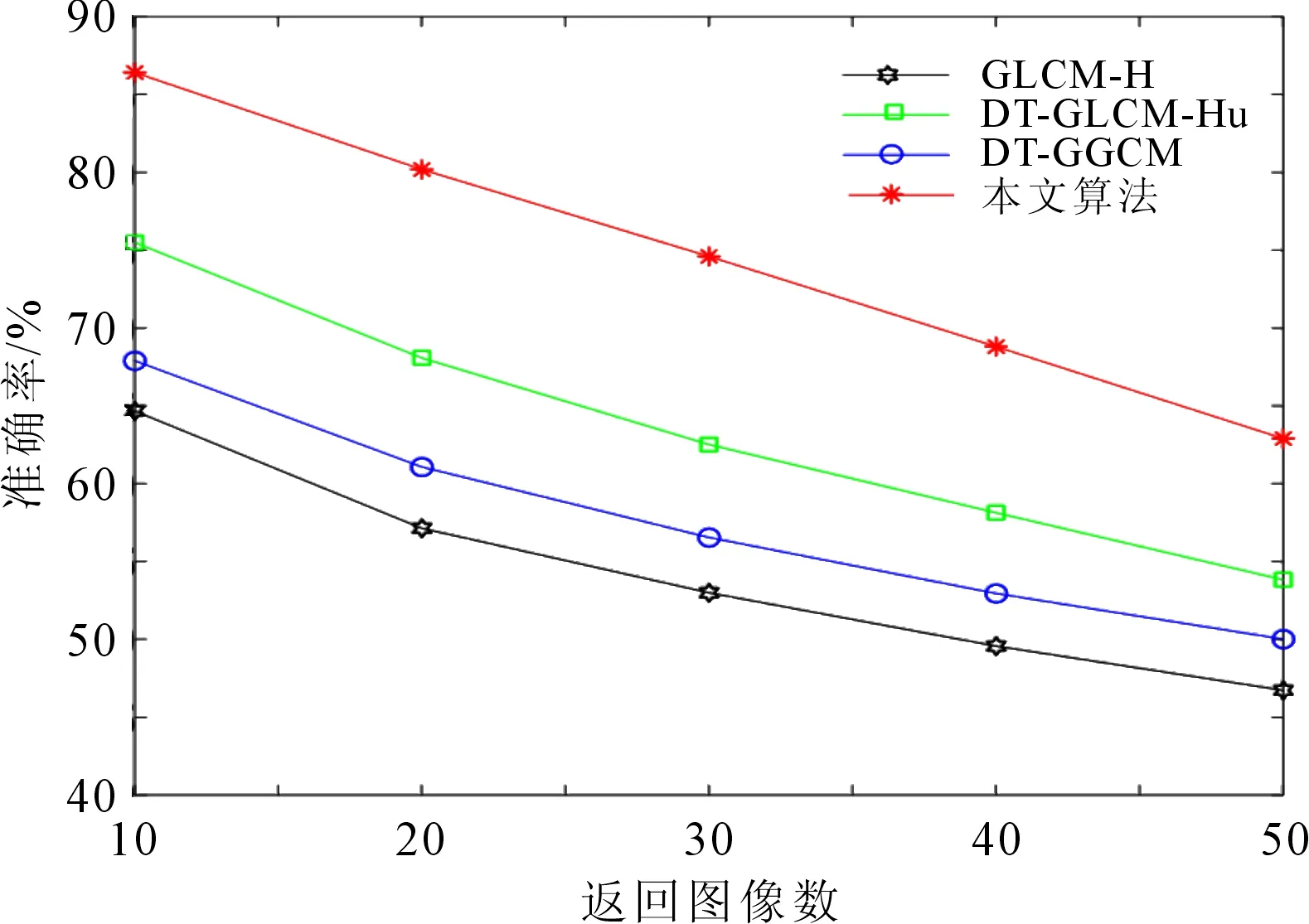
图6 4种检索算法的准确率曲线

图7 4种检索算法的P-R曲线

从图6可见，当检索返回前10幅图像时，本文算法的平均准确率高于同类相关算法中最优算法的10.925%，在返回前50幅图像时，检索的准确率同比高了9.07%。从图7的P-R曲线可以看出，本文算法的检索率与准确率均优于其它3种算法。因此，本文提出的改进纹理特征提取算法应用于现勘图像检索具有一定的有效性。另外，上述实验涉及现勘图像的纹理特征，其结果说明本文算法能够较深入地挖掘出现勘图像的纹理特征，在一定程度上实现对现勘图像的有效刻画，从而提高现勘图像检索算法的检索性能。

6 结语

针对灰度共生矩阵缺少图像纹理的整体空间分布特征与双树复小波变换对图像结构细节敏感的缺陷，提出一种基于改进纹理特征的现勘图像检索算法。改进算法先对图像进行均匀分块，将各个块的角点疏密度与图像细节信息级联，以此表征图像的空间分布特征与结构细节特征，然后对利用双树复小波变换结合灰度共生矩阵提取的纹理信息融合图像的空间分布特征和结构细节特征。在现堪图库上的检索实验结果表明，改进算法能有效地刻画现堪图像的纹理特征，并使得检索算法的检索准确率有一定的提升。

在本文的研究工作中，未考虑到图像的颜色特征。若将图像的颜色作为图像的一个特征，结合本文算法，从多方面对图像的内容进行融合描述，使得检索效果进一步提高和优化，是值得注意的一个方向。