在线学习情感分类模型研究

邱宁佳，沈卓睿，胡小娟，王鹏，高奇

（1.长春理工大学 计算机科学技术学院，长春 130022；2.国网吉林省电力有限公司电力科学研究院，长春 130022）

随着Web 2.0社区的快速发展，社交媒体服务提供商为用户提供了一种方便的方式来共享和创建自己的内容，如在线评论、博客、微博等。通过计算模型从社交中了解这些文本的情感是一个重要的问题，因为这样的模型将帮助人们识别社会事件并做出更好的决策（例如，对库存市场的投资、对观看电影的选择等）［1］。在线梯度下降是一种最基本的在线学习算法，它解决了传统算法无法实时处理数据更新模型的问题，但是得到的稀疏性不理想。Mcmahan等人提出FTRL算法，使参数学习率可根据不同特征的特点自行调整，实践证明算法具有较好的广告点击预测效果［2］。Yang等人通过损失函数的逐渐变化来限制算法的悔界，使得FTRL算法具有渐进变化约束的在线非光滑优化功能［3］。Ta等人将FTRL算法融入到二阶因式分解机中，提出了具有更快收敛速度的FTRFL算法［4］。Huynh等人提出了FTRL-ADP算法，解决嘈杂环境中的概念漂移问题［5］。Sun等人结合自适应滤波原理，设计了FTRLS自适应滤波算法处理线性调频信号，可以有效地恢复干扰噪声的啁啾信号［6］。Orabona等人通过尺度不变性实现对损耗矢量的范数的适应性，使基于FTRL的算法适用于任何有界或无界的决策集［7］。McMahan通过将易于重复使用的引理中的关键参数隔离开来，强化了FTRL分析技术，达到与原始对偶分析一样严格的界限［8］。

学习率是影响在线学习算法结果的重要因素，好的学习率能保证算法快速而准确的收敛到最优值。Kingma等人通过引入和修正一、二阶矩估计，提出了Adam算法，适用于非平稳目标和具有噪声或稀疏梯度的问题［9］。Erven等人提出了MetaGrad方法，它的学习率不会随着时间的推移而单调递减，并且适应各种类型的随机和非随机函数［10］。Timothy等人通过将Nesterov加速梯度法融入到Adam算法，提出了Nadam算法，提高了梯度下降的收敛速度和学习模型的效果［11］。然而自适应学习率算法应用在目标识别、机器翻译等领域中时，得到的优化效果可能不如SGD算法。McMahan和Streeter将AdaGrad进行扩展，提出了延迟容忍算法，当延迟变大时，性能明显优于标准自适应梯度方法［12］。Reddi指出Adagrad算法的关键缺陷，使用指数滑动平均值解决了学习率随着迭代次数的增加而变小的问题［13］。Zhang等人提出了AEDR算法，能够自适应计算指数衰减率，并可将Adadelta和Adam超参数量减少［14］。Chen等人提出了Ada-PGD算法，结合Adagrad和近端梯度下降法，使ADAE具有优异的异常检测性能［15］。

为了提高自适应学习率优化算法的效果，Smith等人提出了周期性学习率方法，只需较少的迭代次数便可达到较高的准确率［16］。Loshchilov等人提出了SGDR算法，能够减少模型迭代次数，并将热启动扩展到修复权重衰减的Adam算法上［17］。陆阳等人在建模基础上，通过为表示情绪特性的轴两端建立模型，使其转换成二层分类器进行加权判别，提出了一种在四分类坐标下建立高斯混合模型进行音乐信号归类的研究方法，解决了音乐情感复杂难以归类的问题［18］。殷宏威等人通过引入组相似度概念，提出一种改进算法，使得当待测样本位于易判区域时，减少KNN大量无用计算，能很快得出判定结果［19］。

本文借鉴Adadelta模拟牛顿迭代求解和Adam对参数更新量进行偏差修正，得到改进的学习率优化算法替换原学习率，得到在线学习LR模型，并以此模型作为情感分类工具，构建完整的在线学习情感分类体系。

1 改进学习率的FTRL-Proximal算法

1.1 改进的学习率优化算法

Adadelta算法解决了Adagrad算法学习率总是衰减、左右更新单位不统一的问题，并具有不需手动设置初始学习率的优点，训练前中期具有良好的加速度，缺点是训练后期易在极值附近发生抖动。Adam算法在Adagrad算法基础上，引入和修正梯度的一、二阶矩估计，使参数更新较平稳，避免了频繁抖动，因此训练后期能够更快的寻到最优值，但仍依赖手动输入全局初始学习率。

为了改善Adadelta算法训练后期的频繁抖动以及Adam算法依赖手动输入初始学习率的问题，本文将Adam算法对梯度的一、二阶矩估计进行偏差修正的做法引入到Adadelta中，命名为Adamdelta：首先使用动量法计算梯度的一阶和二阶矩估计：

其中，ρ1，ρ2为衰减率；gt为损失梯度。再对一阶和二阶矩估计进行偏差修正：

并做拟牛顿迭代处理：

使用Δθ更新累计参数更新量的期望：

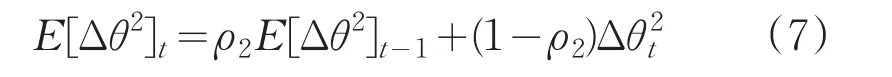
最后使用以上公式更新参数θ，得到最终的更新公式：θt=θt-1+Δθt。

1.2 优化学习率的FTRL-Proximal算法

Adamdelta算法继承了Adam与Adadelta适合处理稀疏数据、学习率自适应调整的特点，解决了Adagrad训练后期累积梯度爆炸导致学习率消失的问题，同时具有Adam更新稳定、Adadelta无需手动搜索初始学习率的优点，因此使用Adamdelta算法来调整FTRL-Proximal的学习率，以期达到提升在线学习算法性能的效果。设定学习率ηt表示为：

迭代步长变化率可表示为：

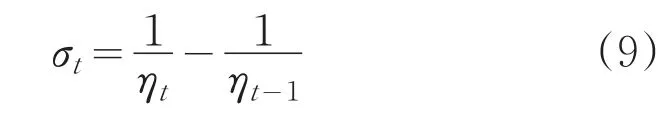
L1正则项系数为λ1，那么，FTRL-Proximal算法的参数更新公式可如下计算：

本文使用Adamdelta算法来替换FTRLProximal的学习率，以期达到提升在线学习算法性能的效果，其更新公式为：

通过上面的推导得到改进FTRL-Proximal算法的参数更新公式，下面给出算法的流程。

images/BZ_109_246_2635_1192_2689.png输入：L1正则项系数 λ1，衰减率 ρ1，ρ2，ρ3，常数∈输出：参数θ 1 初始化 θ1，1，...，N,z1，1，...，..，N,v0，1，...，N=0 ，E[N=0 ，一阶和二阶矩m0，1，.Δθ2]0，1，...，N=0 ，ρ1=0.9 ，ρ2=0.999，ρ3=0.95，∈=10-8 2 fort=1 toT do 3 学习优化目标损失函数ℓt 4 for alli∈N do 5 计算

gt,i=∂ℓi(θt)θt,i E[Δθ2]t-1+∈代入公式（13）计算 σt；使用公式（1）-（4）一阶和二阶矩估计进行偏差修正对使用公式（5）修正参数变化量的均方根偏差R̂t使用公式（6）更新参数Δθt,i使用公式（7）更新参数历史累计量E[Δθ2]t,i使用公式（14）计算zt RMS[Δθ]t-1=6 使用使用公式7 end for 8 end for∈更新学习率（8）-（12）更新参数θt R̂timages/BZ_109_1492_947_1612_994.png

2 基于在线学习的情感分类模型

2.1 Doc2vec模型

Word2vec模型通过训练得到词向量，通过计算词向量之间距离度量词语间关系，但缺乏对句子和文本之间语义分析的能力。因此，Quoc Le和Tomas Mikolov在Word2vec的基础上提出了Doc2vec模型［20］。Doc2vec除了增加一个段落向量以外，其他地方同Word2vec几乎相同，包括PV-DM和PV-DBOW两个模型。

PV-DM模型利用上下文和增加的段落向量预测单词概率，增加的一个段落向量保存句子或文本的语义信息。每一个段落向量唯一标识一个句子或文本，在同一个句子或文本训练过程中，词向量共享一个段落向量。将段落向量和词向量加和取平均或连接起来作为Softmax函数的输入。PV-DBOW则是利用段落向量来预测段落中一组随机单词的概率。

2.2 在线学习情感分类模型

对于中、英文情感信息数据，需分别对其进行分词、去停用词、过滤标点符号和过滤标点符号、去停用词、变化大小写等预处理。然后使用Doc2vec模型对预处理后的情感信息进行训练，得到段落向量和词向量表示。得到了句子或文本的向量表示后，使用在线学习分类模型对其进行在线训练，通过不断的学习和更新模型，来提高模型的分类能力。经过一段时间学习后，模型的分类能力达到预期效果，便可对未知情感类别的文本或语句进行情感分类。整个模型的示意图如图1所示。

图1 在线学习情感分类模型

2.3 在线学习逻辑回归算法

传统的逻辑回归通过训练大量样本可得到精度较高的分类模型，但将大量样本加载到内存中，对计算机内存要求很高。若样本数量超出计算机内存，则无法进行模型训练。本文采用在线学习来训练模型，每训练完一个样本就对模型更新一次，降低了对计算机内存的要求。使用改进学习率优化算法的FTRL-Proximal取代梯度下降来更新逻辑回归模型的参数，得到在线学习逻辑回归模型，算法的流程如下。

images/BZ_110_246_1677_1192_1731.png输入：L1正则项系数 λ1，衰减率 ρ1，ρ2，ρ3，常数∈输出：特征属性的权重参数θ 1 初始化 θ1，...，N,z1，...，N=0 ，一阶矩和二阶矩 m0，1，...，N,v0，1...N=0 ，E[Δθ2]0，1，...，N=0 ，ρ1=0.9，ρ2=0.999，ρ3=0.95，∈=10-8 2 while停止条件3 从训练样本集中取一个样本(xt,yt)4 假设函数hθ(xt)5 损失函数J(θ)6 for alli∈N do gt,i=(hθ(xt)-yt)xt i更新参数θ #优化学习率的FTRL-Proximal算法7 end for 8 end while

3 实验与结果分析

3.1 实验环境与数据

为了验证改进学习率优化算法的效果，在Ubuntu Kylin 16.04系统上进行实验，实验程序为Python2.7所编写。实验数据为IMDB电影评论文本，数据包括两类，一类为乐观评论，一类为悲观评论，每类评论25 000篇。训练集和测试集按1∶1的比例分配，即均包含乐观评论和悲观评论各12 500条。如表1所示。

表1 数据集

3.2 数据预处理

对文本评论数据先进行分词处理，然后去停用词、标点符号之后，输入到Doc2vec模型中，训练得到每篇文本的向量表示。Doc2vec采用PV-DM模型来进行训练，使用负采样来进行优化，负采样噪声词数设置为5，滑动窗口大小设置为10，输出特征向量的维度设置为100。将得到的文本特征向量作为分类模型的训练集和测试集，两者的比例为1∶1。

3.3 评价指标

在分类问题中，常使用混淆矩阵对分类结果进行可视化，二分类的混淆矩阵如表2所示。

表2 混淆矩阵

表中，TP表示被预测为正的正样本，FN表示被预测为负的正样本，FP表示被预测为正的负样本，TN表示被预测为负的负样本。基于混淆矩阵计算如下指标：

（1）准确率：Accuracy=(T P+TN)/(TP+FN+FP+TN)；

（2）精确率：Precision=TP/(T P+FP)；

（3）召回率：Recall=TP/(T P+FN)；

（4）F1值：F1=2×Precision×Recall/(Precison+Recall)；

3.4 实验结果分析

3.4.1 实验1：学习率优化算法对比

为了直观了解各个优化算法的特点，对比每个算法的优缺点，通过在马鞍面（z=-2(x2-y2)）上的三维运行轨迹以及二维等高线上的轨迹，来对算法进行可视化展示。使用SGD、Momentum、Adagrad、Adadelta、Adam作为对照算法，与本文改进算法Adamdelta作对比。通过多次实验，将各个算法的参数设置如下表所示，得到如图所示轨迹图，“-”表示算法无此参数。此外，将SGD、Adagrad、Adam算法初始学习率η设置为0.05，Momentum初始学习率η设置为0.01。

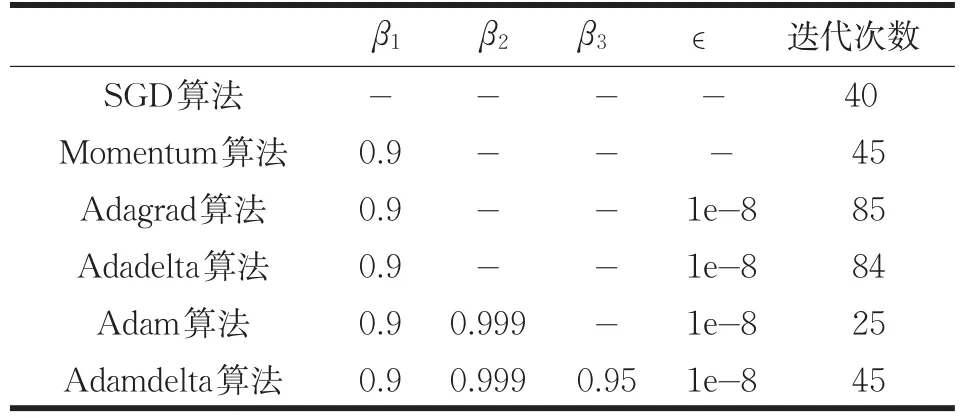
表3 各算法参数设置

由此，得到如图2所示轨迹图，图3为图2在二维等高线上的对应图，源自相同的参数设置。通过实验发现，如果将算法在x轴的初始位置设置为0，所有算法都将陷入马鞍面的中心（0，0，0）点；因此将算法的初始位置设置为（0.001，0.8），通过表3中迭代次数达到图2所示位置。图中每个标记点代表经过一次迭代后的位置。

图2 三维马鞍面上运行轨迹图

图3 二维马鞍面等高线上轨迹图

结合图2和图3可以看出，SGD算法的轨迹总是沿着梯度下降最快的方向更新，因此每次更新方向只跟当前梯度有关。Momentum算法运行到中心位置后不能立刻调整方向，是因为其更新方向结合了上次更新方向和当前梯度下降方向。Adagrad算法前期每步更新距离较大，后期更新距离越来越小，是由于其使用累积梯度平方和作为学习率的分母项，因此随着迭代次数增加，学习率越来越小。从表3中可以看出，Adagrad迭代了85次才到达图2中的位置，相比其他算法这个迭代次数最多。Adadelta算法前期每步更新距离较小，后期更新距离较大，这是因为其省去了手动设置初始学习率的步骤，因此前期更新速度受∈值的影响较大，此处∈值为1e-8，因此初始更新距离较小，如果将∈值设置成1e-4，只需要迭代12次便可到达图2所示位置，可以看出这个更新速度比其他算法都快，因此后期会出现抖动情况。Adam算法每次更新距离差别不大，是因为其对梯度进行了偏差修正，因此算法比较稳定。Adamdelta算法前期每步更新距离相比Adadelta要大，是因为算法对参数更新量进行了偏差修正，因此算法启动速度比Adadelta要快；随着迭代次数增加，算法更新趋于稳定，更新方向合理。表明改进学习率算法相比Adagrad解决了学习率消失的问题，同时具有Adam算法更新稳定，Adadelta算法不用手动搜索一个合适的初始学习率，且不会启动过慢的优点。

3.4.2 实验2：在线学习情感分类效果对比

为了度量算法对分类器的影响，分别使用SGD、Momentum、Adagrad、Adadelta、Adam以及本文提出的Adamdelta算法，结合LR分类器，使用在线学习对经过Doc2vec模型处理的情感数据进行分类。各算法的参数设置如表4所示，为防止Adadelta启动过慢，将其参数∈设置为1e-4。此外，将SGD、Momentum、Adagrad、Adam初始学习率η设置为0.01。

表4 各算法参数设置

将起始迭代次数设置为100，最大迭代次数设置为7 100，每轮增加250次，得到各算法在不同迭代次数下的分类准确率，如图4所示，以及各算法消耗的时间，如图5所示。其中，改进方法与传统方法特征词提取示例如表5所示。

图4 分类准确率对比

图5 消耗时间对比

表5 特征词提取示例的比较

从图4中可以看出，Adamdelta算法的准确率明显比SGD，Momentum，Adagrad，Adadelta的准确率高，相比Adam也有小幅度提升。另外迭代次数大于3 500次后，SGD，Momentum，Adagrad，Adadelta的准确率基本不再提高，而Adam和Adamdelta的准确率随着迭代次数的增加仍在上升。说明本文提出的Adamdelta算法解决了Adagrad训练后期学习率消失导致算法效果无法提升的问题。从曲线的变化趋势可以看出，Adamdelta比其他算法更稳定。说明引入Adam偏差修正的做法对梯度和参数更新量进行偏差修正，对于提升算法的稳定性有良好的效果。从图5中可以看出，SGD，Momentum，Adadelta以及Adamdelta算法消耗的时间几乎相同，而Adagrad和Adam算法消耗的时间是前者的3倍多。说明Adamdelta继承了Adadelta训练速度快的优点。通过准确率和时间的对比表明，本文提出的改进学习率算法相较于Adagrad，无论是分类准确率还是速度上都有明显的优势，相比Adadelta准确率上有一定优势，相比Adam训练速度上有明显优势。从表5中可以看出，相同的样本分别使用改进的方法和传统的方法进行特征提取，改进的方法提取出了传统方法没有提取出的特征词，进而提高了分类精度。例如，改进算法提取出yawn，imitation等词语，但传统的算法没有提取出。

3.4.3 实验3：离线学习与在线学习情感分类效果对比

使用LR分类器作为离线学习的分类模型，利用批量梯度下降来更新LR模型的参数，使用基于Adagrad的FTRL-Proximal结合LR得到的在线学习分类模型，以及基于Adamdelta的FTRL-Proximal结合LR得到的在线学习分类模型，分别对经过Doc2vec模型处理的情感数据进行离线学习和在线学习。由于离线学习和在线学习每次迭代使用的样本数量不同，因此不以相同迭代次数的结果来进行对比，而是以各自模型达到最佳效果时的分类指标和训练时间来进行对比。实验发现离线学习模型迭代至140次时结果稳定，各指标值基本不再变化，在线学习模型迭代至6 000次时各指标值稳定，因此将离线学习模型迭代次数设置为20至140次，每轮增加10次，将在线学习模型迭代次数设置为100至6 100次，每轮增加300次，得到分类准确率、精确率、召回率、F1值和训练时间对比如图6、图7所示。

图6 学习模型的评估指标分析

对比图6中三个模型的各项分类指标值可以看出，离线学习模型的准确率与原FTRL-Proximal算法差别不大，而改进FTRL-Proximal算法的准确率相比离线学习和原算法提升了1%～2%。对比精确率、召回率和F1值可以看出，相比离线学习模型，在线学习模型的召回率偏高，精确率偏低，F1值稍高。表明在线学习模型偏向于将悲观评论预测为乐观评论。对比图7三个模型的训练时间可以看出，模型达到最佳训练效果时，离线学习模型消耗的时间是原在线学习模型的2倍左右，是改进在线学习模型的6倍左右。说明在线学习模型相比离线模型训练速度有很大的优势，而改进的在线学习相比原算法的训练速度也有明显的提升。相比离线学习模型，改进学习率的在线学习模型不仅准确率有所提升，训练时间更是大大缩短，说明本文提出的在线学习情感分类模型具有一定的可行性。

图7 学习模型的耗时分析

4 结论

本文首先对FTRL-Proximal算法的学习率进行了分析，针对其学习率在训练后期消失的问题，对参数更新量的均方根以及梯度的一阶和二阶矩估计进行偏差修正，然后再使用改进的FTRL-Proximal算法来迭代求解LR模型的参数，得到在线学习LR模型。以此模型作为情感分类模型的分类器，使用Doc2vec工具生成的文本特征向量作为模型的输入向量，构成了完整的在线学习情感分类模型，通过实验验证出改进学习率优化算法具有更好的分类效果，以及改进学习率的在线学习模型具有更高的准确率，和大大缩短的训练时间。