基于声发射与小波变换的阀门泄漏研究

刘 影，周 敏，邓 昊，李卓航，赵康建

（西南石油大学，成都 610500）

0 引言

阀门是管道结构的重要组成部分，它能够实现管道介质的流量流向控制，同时也可以切断流体，改变管道内部的压力，是管道结构中的控制核心。由于它能够起到这样的控制和保护作用，所以阀门被广泛地运用在了石油石化、燃料运输、化学、造船业等众多的产业当中。但是，在长期的使用过程中，阀门会产生一定程度的破坏。在管道中的高压和不同设备的温度条件下，或者是石油化工等高腐蚀性的环境中，阀门的频繁开闭和长期使用都会导致阀门的磨损、变形，从而出现泄漏的情况，并且带来极大的经济损失和安全隐患。

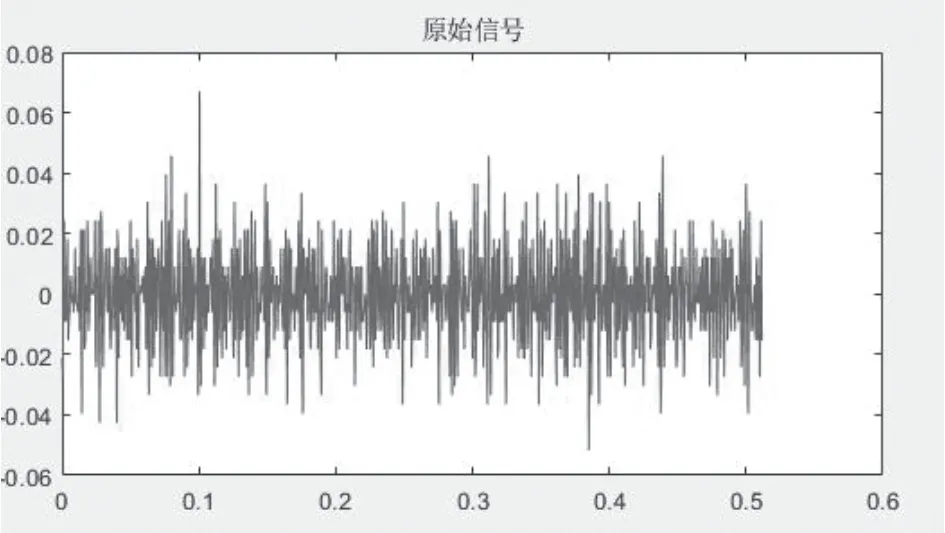
图1 无泄漏时域原始信号图Fig.1 No-leak time domain original signal diagram

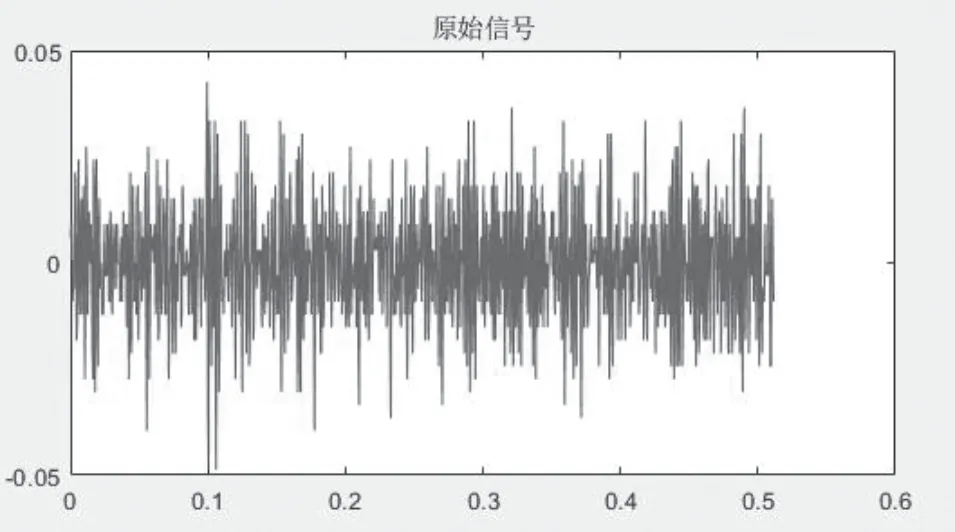
图3 开度0.01原始时域信号图Fig.3 Opening degree 0.01 original time domain signal diagram

1 声发射检测原理

压力管道泄漏所产生的声发射信号是广义的声发射信号，管壁本身不释放能量而只是作为一种传播介质。泄漏过程中，在泄漏点处由于管内外压差，使管道中的流体在泄漏处形成多相湍射流，这一射流不但使流体的正常流动发生紊乱，而且与管道及周围介质相互作用向外辅射能量[1]，在管壁上产生高频应力波。实验所使用的声发射探头是一种压电晶体式，当阀门泄漏时质点的运动传递到传感器的接触面的时候，带动压电陶瓷上的质子运动，从而对压电陶瓷产生压缩和拉伸的效果，进而转换为电压信号，送入信号处理器，完成应力波到电信号波的转变过程[2]。

2 管道泄漏检测实验

2.1 实验方案

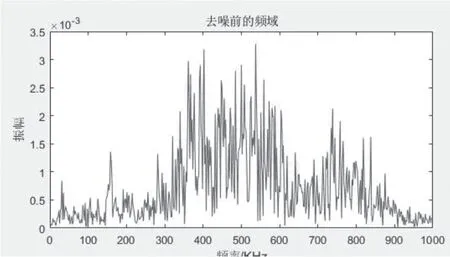
图2 无泄漏频域原始信号图Fig.2 No leakage frequency domain original signal diagram

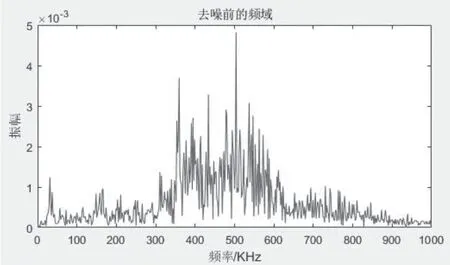
图4 开度0.01原始频域信号图Fig.4 Opening degree 0.01 original frequency domain signal diagram

将声发射探头固定在阀门上，连接并调试声发射ASYM-6 仪器，关闭阀门，打开一阶水箱循环系统控制台和水泵，开始实验。在相同压力下进行实验，在无泄漏的时候检测一组信号，然后依次改变阀门开度大小，检测多组数据。阀门的声信号频带范围在0kHZ ～250kHZ，声发射仪器采集信号频率位2MHZ，每次采集数据点1024 个。

2.2 阀门泄漏信号频段确定

声发射探头能够检测很微弱的信号，检测的信号中包含大量的环境噪声。首先在阀门无泄漏的情况下检测一次信号，通过傅里叶变换将时域信号转为位频域信号。在阀门开度0.01 时检测一组数据。阀门无泄漏时域原始信号如图1 所示，无泄漏时域原始信号如图2 所示。阀门开度为0.01 原始时域信号如图3 所示，原始频域信号如图4 所示。

对比可知，频带300kHZ ～400kHZ 的信号不是由阀门泄漏引起的，经查阅资料，是由电磁阀噪声引起的。

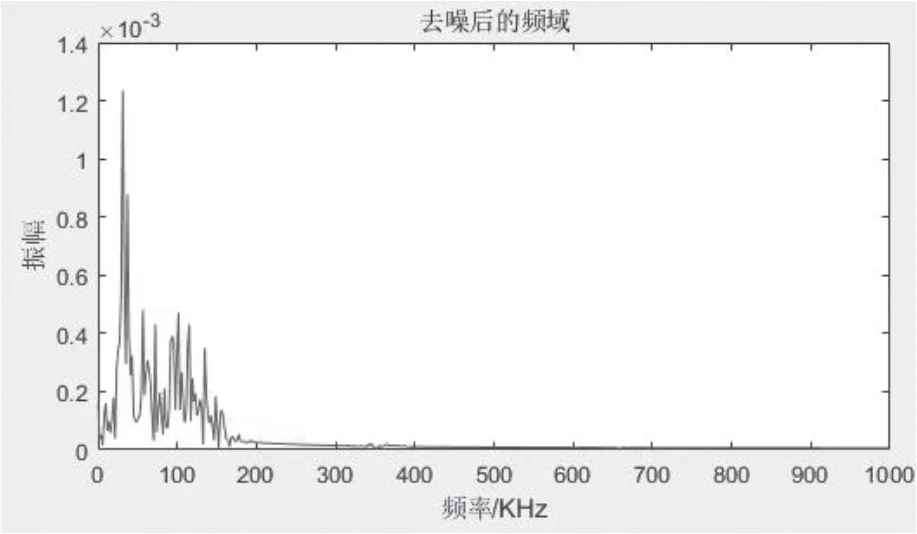
图5 开度0.01去噪后频域信号图Fig.5 Frequency domain signal diagram after 0.01 degree denoising

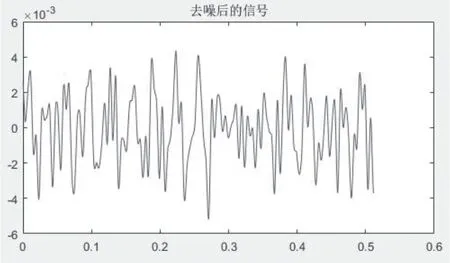
图7 阀门开度0.01去噪信号图Fig.7 Valve opening degree 0.01 denoising signal diagram

如图5、图6 所示，当阀门开度为0.01 与0.03 时，在30kHz ～40kHz 之间有一个谱峰，随着泄漏量的增加，频谱幅值也在增加。在阀门泄漏不同开度的频域图中，皆可找到如此的规律，由此可以判断，阀门泄漏声信号频带在30kHz ～40kHz。

2.3 声发射信号处理

在实验中使用的小波去噪方法为小波阈值去噪，其基本思想是将小波信号与噪声信号通过小波变换来进行分离，它的信号模型可表示为：

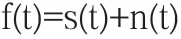
s(t)为原始信号，n(t)为噪声信号。

经过小波分解后，有效信号的小波系数要大于噪声信号的小波系数，可以找到一个λ 来作为阈值。当分解系数小于阈值的时候，识别其为噪声并将其剔除；大于阈值时，认为其为有用信号，并将其保留[1]。阀门为开度0.01 时，小波阈值去噪后的时域信号幅值为4mv 左右，阀门开度为0.03 时，小波阈值去噪后的时域信号幅值为5mv 左右。去噪后时域图如图7、图8 所示。

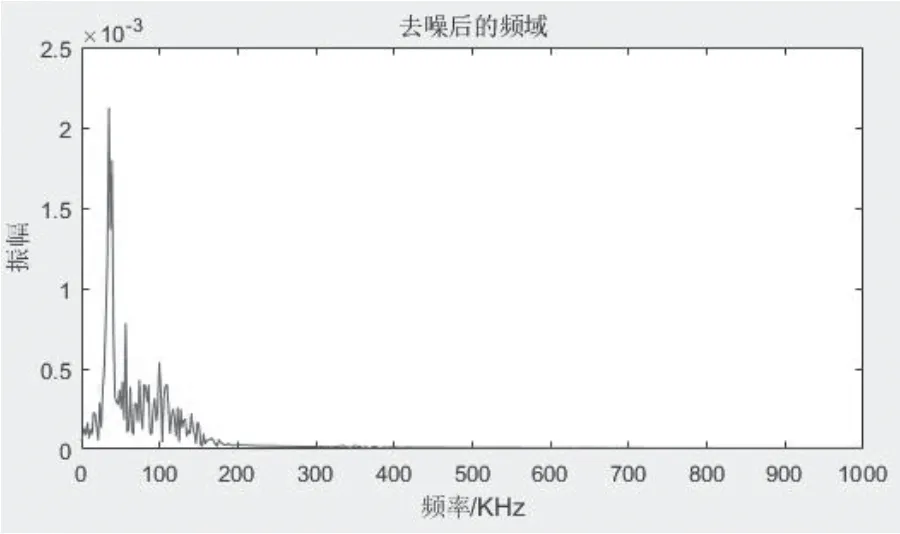
图6 开度0.03去噪后频域信号图Fig.6 Frequency domain signal diagram after 0.03 denoising

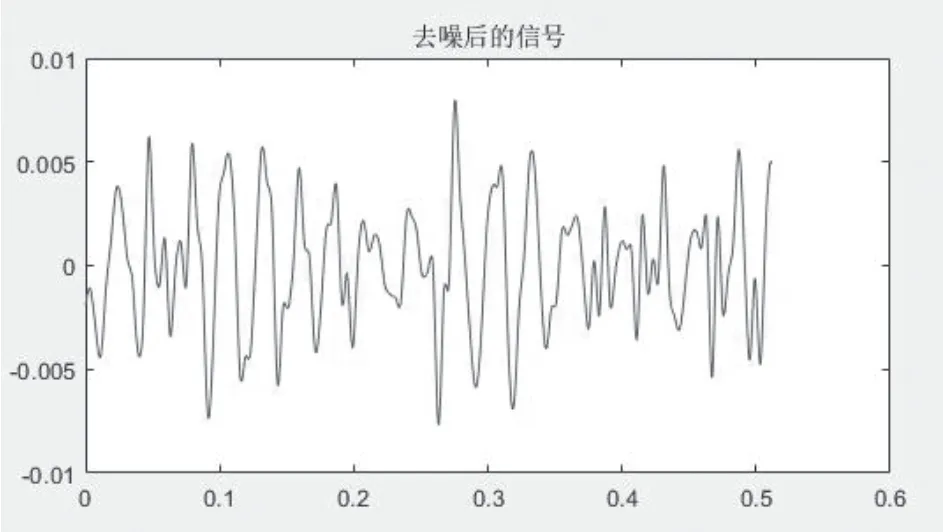
图8 阀门开度0.03去噪信号图Fig.8 Valve opening degree 0.03 denoising signal diagram

时域分析只能观察泄漏信号的电压幅值，而不能明确地观察出泄漏有效信号的其它特性，所以需要通过傅里叶变换将时域信号转换为频域信号。将泄漏声信号处理到频域进行分析，可以得出泄漏有效信号的频段分布和泄漏尖峰信号分布。从频域图9 分析，随着泄漏的增大，频谱幅值也相应增加。红色轨迹为阀门开度为0.03 时的频域图，蓝色为阀门开度为0.01 的频域图。

2.4 声发射信号小波包分析

与小波分析不同，小波包进行分解和重构能更好地处理信号中大量的细节和边缘信息，并且对高频信号的分解也毫无疏漏，能够更好地进行时频的局部化分析[3]。对泄漏声信号进行小波包分解处理之后，可以计算每个频段的能量值来得到声信号的能量分布特征，从而观察出泄漏量与能量之间的关系。系统采样率为2MHz，奈奎斯特频率为1MHz，根据小波包分解原理，选取db3 为小波基，将阀门泄漏信号分解为6 层，共64 个小波包，每个子频段为15.625kHz。不同阀门开度下，声发射信号的能量特征图如图10 ～图14 所示.

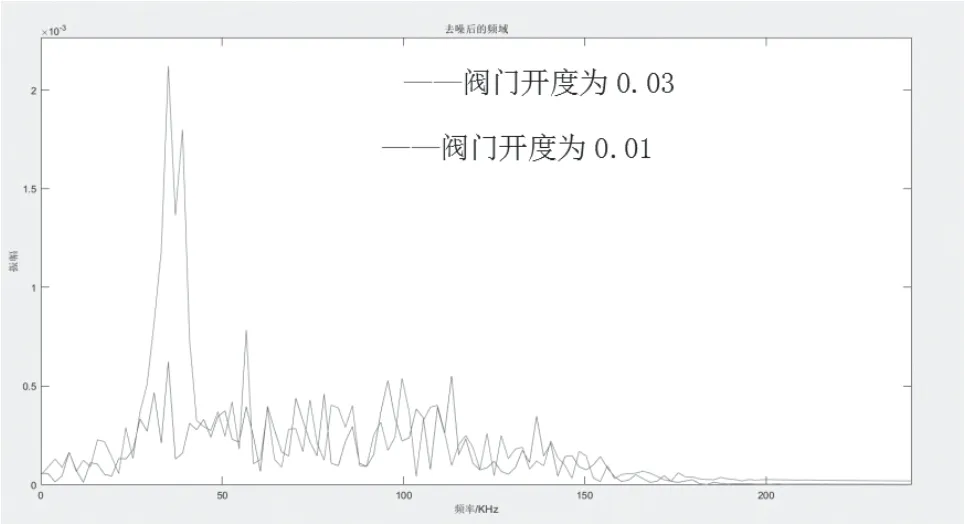
图9 不同开度信号频域图Fig.9 Spectral diagram of different opening signals

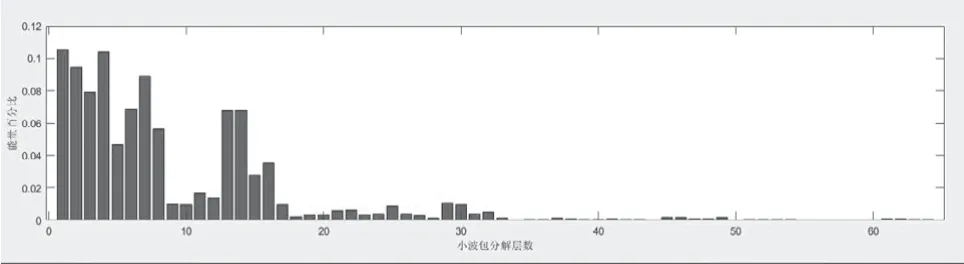
图10 阀门开度0.01的能量特征图Fig.10 Energy characteristic diagram of valve opening degree 0.01

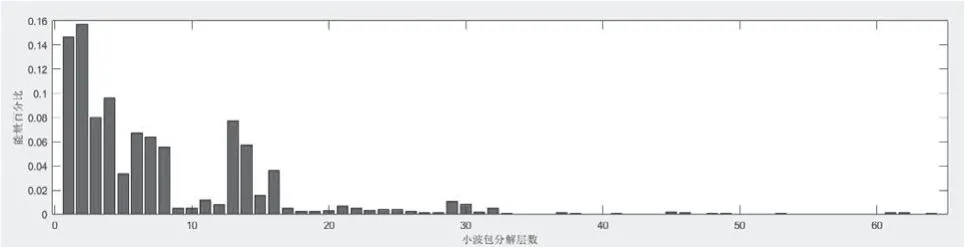
图11 阀门开度0.03的能量特征图Fig.11 Energy characteristic diagram of valve opening 0.03

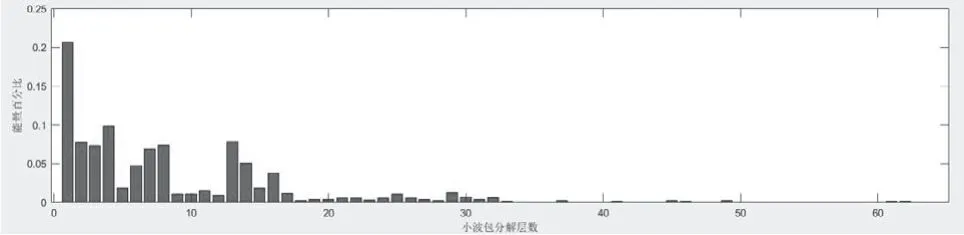
图12 阀门开度0.05的能量特征图Fig.12 Energy characteristics of valve opening 0.05

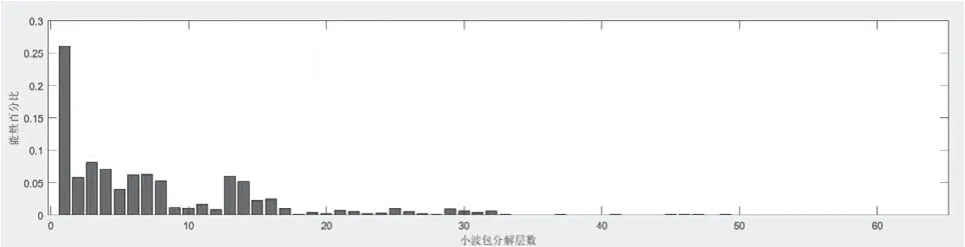
图13 阀门开度0.07的能量特征图Fig.13 Energy characteristic diagram of valve opening 0.07

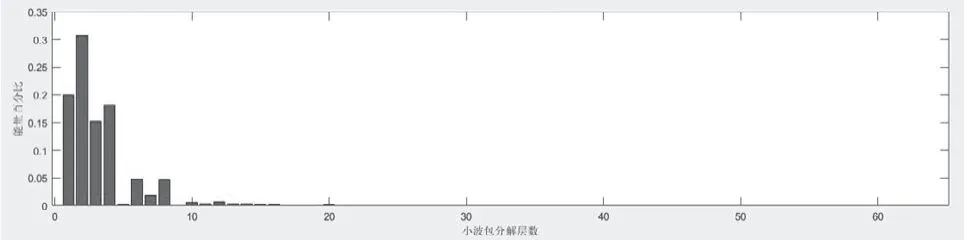
图14 阀门开度0.15的能量特征图Fig.14 Energy characteristics of valve opening 0.15

2.5 声发射信号及其能量特征分析

小波包分解第一个子频段为0kHz ～15.625kHz，第二个子频段为15.625kHz ～31.25kHz，通过之前的分析得知，声发射信号的有效频段在30kHz ～40kHz。能量值在能量特征图中分别对应第二段能量柱所对应的能量值。从声发射信号的能量特征图可得，随着阀门开度的增加，声发射信号能量值逐渐增大，在阀门开度较小时，能量值最主要频段为15kHz 左右，随着阀门开度逐渐增大，在声发射有效频段30kHz 左右的能量最为明显。

3 结论

1）通过时域分析得知，阀门泄漏产生的声发射信号幅值随着阀门开度（模拟泄漏率）的增大而增大；通过频谱图分析得知，阀门泄漏产生的声发射信号频段主要集中25kHz ～40kHz，随着阀门开度增大，频谱幅值也随之增大。

2）阀门声信号在不同开度下，同一频段的能量值不同，随着阀门开度的增加能量值逐渐增大。