具有加权梯度源项的半线性抛物方程解的爆破时间下界❋
马羚未, 方钟波
(中国海洋大学数学科学学院,山东 青岛 266100)
迄今为止,已有许多学者致力于抛物型方程解的整体存在性与爆破现象及定性性质方面的研究,且已有许多专著和综述性的成果(见文献[1-4])。特别是,Quittner和Souplet专著[2,第 3,4章]中详细介绍了具有Dirichlet边界条件和常系数a的反应-扩散模型中解的定性性质。粗略地概括,爆破的发生以及类型依赖于常数系数a,初始值以及区域的选取,且梯度模型的另一个显著特点是在适当的条件下可能发生边界或内部中梯度爆破现象。最近,爆破问题中爆破时间的上下界估计的研究方面有新的进展。实际上,关于抛物型方程解发生爆破时爆破解的爆破时间上界(见文献[5]中六种方法)的技巧较多。然而,爆破解的爆破时间下界一般较难确定且大部分文献限制在三维空间中,主要困难在于Sobolev最优化常数的确定。这里提供给读者参考文献[6-9](不含梯度项),文献[10-13] (含梯度项)及相关文献。特别地, Marras在文献[11]中研究了如下具有齐次Dirichlet边界条件和梯度源项的半线性抛物型方程组的初边值问题
并在三维空间中具有光滑边界的凸区域上得到了解发生爆破时爆破时间的下界。
关于具有空变系数的反应模型,Song和Lv[14,15]最近研究了具有加权内部源项的局部抛物型方程
ut=Δu+axf(u), (x,t)∈Ω×(0,t*),

a1:ax>0,x∈Ω;ax=0,x∈∂Ω,或



其中c,c1,c2为正常数。当初边值问题具有非线性Neumann边界条件,且权函数满足a1或a3或a4时,得到了三维空间中问题解发生爆破时爆破时间界的估计(见文献[14])。在文献[15]中,考虑了问题具有齐次Dirichlet和齐次Neumann边界条件且权函数满足a1或a2的情形,在高维空间中得到了初边值问题解的爆破时间界与爆破速率的估计。
综上所述,在高维空间(N≥3)上具有加权梯度源项的半线性抛物型方程Dirichlet初边值问题解的爆破分析方面的研究还未得到展开。因为方程中含有加权梯度源项,所以微分不等式技巧的应用中遇到困难。本文中,受Marras[11]工作启发,在高维空间中考虑具有加权梯度源项的半线性抛物方程
ut=Δu+axf▽u,x,t∈Ω×0,t*,
(1)
给出齐次Dirichlet边界条件和初始条件
ux,t=0,x,t∈∂Ω×0,t*,
(2)
ux,0=u0x,x∈Ω。
(3)

a1:ax>0,x∈Ω;ax=0,x∈∂Ω,或者


非负初始值u0x为C1类连续函数且满足相容性条件。因此,由抛物方程经典理论可知问题(1)~(3)存在唯一的非负古典解。解的最大存在时间t*∈(0,+∞]。此外,若t*<+∞,则ux,t以C1-范数意义下在有限时刻发生爆破(见文献[16,定理 10,p.206]);即
模型(1)常常称为具有黏性的Hamilton-Jacobi方程且与物理学理论中描述界面生长及粗化的Kardar- Parisi-Zhang方程有密切联系,见文献[17-18]以及相关文献。本文的目的是在高维空间中适当的加权测度意义下建立问题(1)~(3)解发生爆破时爆破时间下界的估计,并给出应用举例。
1 爆破时间t*的下界
本节中,将在新的加权测度意义下给出问题(1)~ (3)爆破解的爆破时间的下界估计。
定理1令ux,t是问题(1)~(3)的非负古典解,且ux,t在有限时间t*发生爆破。假设非负函数f▽u满足

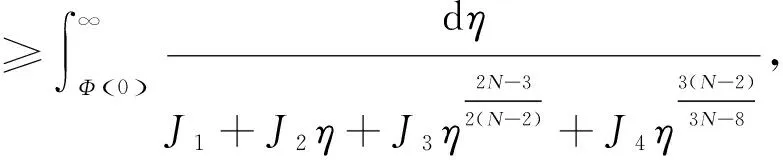

证明:首先,对Φt求微分,并利用(1),(2),Green公式,H1以及a5,可以得到
Φ′t=


(4)
由于0<β<1,现在,对(4)不等号右端最后一项运用Young不等式,导出


(5)
然后,再对(4)不等号右端的第一项运用Hölder不等式以及Young不等式,算出


(6)
式中ε1是待定的正常数。
将(5),(6)代入到(4)中,整理得到


(7)
从而,对(7)不等号右端的最后一积分项运用Hölder不等式及Young不等式,可得

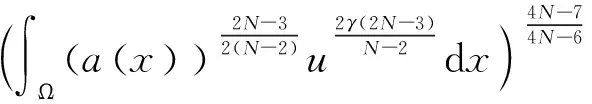

(8)

之后,再次利用Hölder不等式,则不等号(8)右端的第一项变为
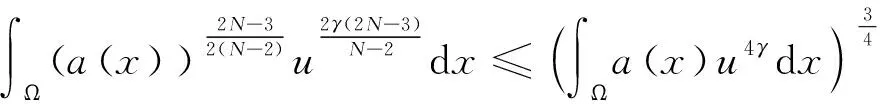
(9)
由此,运用高维空间N≥3中Sobolev不等式[19]知
其中Cs是Sobolev最优化常数。同时,利用假设a5及Jensen不等式,有

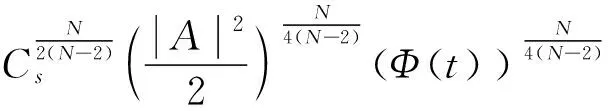
(10)
现在,将(10)代入到(9)中,并利用Young不等式,可以导出


(11)
其中ε2是待定的正常数。
最后,将(8)~(11)代入到(7)中,整理可得

(12)
其中
此时选取ε1>0充分小,ε2>0使得J5=0。故(12)变为

(13)
对(13)从0到t*积分,最终导出

故定理1证毕。
注1:问题(1)~(3)中,若齐次Dirichlet边界条件(2)替换为齐次Neumann边界条件,则可以得到与定理1类似的结论。事实上,此时Sobolev型不等式变为
从而,(10)变为
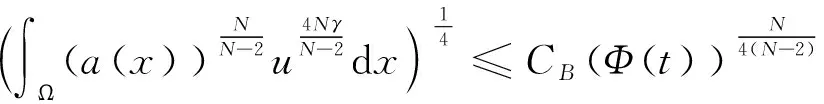
其中
易得爆破时间t*的下界为

其中
这里ζ1>0充分小,ζ2>0使得

2 例题
本节中,将通过举例来验证定理1。
例1 令ux,t是如下问题的非负古典解:
u=0,x,t∈∂Ω×0,t*,
ux,0=1-x>0,x∈Ω,
其中Ω是R3中的单位球,给定


因此,由定理1知爆破时间的下界为
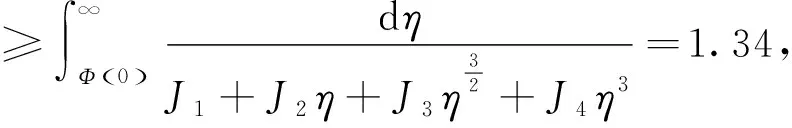

3 结语
本文中,运用修正的微分不等式技巧,研究了高维空间中具有加权梯度源项的半线性抛物方程Dirichlet初边值问题解爆破时间。给出了当爆破发生时,在加权测度意义下解爆破时间的下界,并给出具体实例说明了研究结果的有效性。

