吸气式高超声速飞行器热气动弹性研究进展
杨超,赵黄达,吴志刚,*
(1.北京航空航天大学 航空科学与工程学院,北京100083;2.航空器先进设计技术工业和信息化部重点实验室,北京100083)
吸气式高超声速飞行器飞行马赫数大于5,普遍采用超燃冲压发动机作为推进系统,由于不需要携带氧化剂,飞行器的航程增大,入轨更加灵活[1]。吸气式高超声速飞行器同其他高超声速飞行器一样,同样存在着热颤振、气动伺服弹性稳定性、壁板颤振等相关气动弹性问题。
笔者所在团队曾在2010年对高超声速飞行器的气动弹性力学问题进行过综述[2],并对气动推进/气动弹性耦合问题进行了一定的介绍。但近十年来,吸气式高超声速飞行器的热气动弹性问题得到了越来越多的关注,随着研究的推进,许多新的认识也不断产生。
吸气式高超声速飞行器通常采用机体/发动机一体化构型设计,这种构型存在着多个学科间的交叉与耦合,形成了气动-伺服-热-弹性-推力(ASTEP)[3]综合问题。吸气式高超声速飞行器,作为高超声速飞行器的一种,除了面对传统的热气动弹性问题,由于特殊的推进系统的引入,飞行器系统产生的特殊而复杂的气动弹性问题需要引起关注。其气动弹性问题的特殊性和挑战性主要体现在以下方面:
1)机体/发动机一体化构型带来的动力学耦合问题
吸气式高超声速飞行器的前体下表面通常作为发动机的预压缩面,通过数道激波达到超燃冲压发动机的工作条件;后体下表面作为发动机喷管的一部分,产生推力以及附加升力。这样的构型,使得机体及推进系统产生控制以及飞行力学、气动弹性动力学等方面的耦合问题。刚体与弹性振动引起的飞行迎角的变化会影响发动机入口条件,从而导致发动机推力的敏感变化,推力反过来影响飞行器的姿态控制、气动弹性特性,造成复杂的动力学耦合问题。
2)刚弹耦合的动力学问题
吸气式高超声速飞行器通常采用细长体构型,为了满足高超声速巡航要求,往往需要较大的燃油质量系数。此外,该类飞行器多使用轻质薄壁结构,并面临高速飞行带来的气动加热效应。这几个方面的因素共同导致了机体固有频率的降低,且具有较大的频率变化范围。机体的低阶弹性模态频率将更加接近其刚体飞行动力学频率,系统刚弹耦合问题越发严重。
3)气动弹性强不确定性问题
吸气式高超声速飞行器面临的宽马赫数飞行条件、复杂气动力/热环境、动力学/控制耦合等问题,给全机系统分析带来了许多困难,对控制系统的设计提出了新的挑战。推进系统涉及复杂流体力学、燃烧动力学问题,本身同样存在不确定性问题,其引入更是增加了问题的复杂度,因此需要有效的飞行控制方法及不确定分析方法保证飞行器的稳定性及飞行品质。
针对上述吸气式高超声速飞行器的新特点,本文着重介绍了该类飞行器的建模及气动弹性动力学问题的研究进展,希望能为相关研究人员提供一定的参考。作打下了基础。国内唐硕等[5]基于一维流动理论,建立了类似的适用于飞行动力学分析的刚体推进系统模型,并讨论了飞行参数对于推进系统性能的影响规律。
在一维模型基础上,MASIV(Michigan-AFRL Scramjet In Vehicle)、SRGULL等二维分析程序考虑了更多影响因素,对超燃冲压发动机进行了更高精度的建模仿真。
MASIV发动机分析程序[6-9]考虑了:①隔离段的预燃烧激波串效应;②气体解离和复合反应导致的总压损失;③壁面传热及摩擦效应;④燃料空气混合情况;⑤有限速率燃烧和自点火反应机理。通过求解一系列微分方程组,得到发动机各状态量的分布情况。MASIV程序建立的超燃冲压发动机模型示意图见图2。
Torrez等[8]为了验证MASIV程序的有效性进行了试验研究,试验装置示意图以及计算程序使用的简化模型见图3,试验结果与计算得到的
1 吸气式高超声速飞行器一体化建模研究进展
1.1 适合全机动力学耦合分析的超燃冲压发动机建模进展
从该类飞行器的特点可以看出,吸气式高超声速飞行器性能的准确估计不仅需要考虑机体的相关动力学特征,推进系统同样是关键部分,有必要对超燃冲压发动机建模进行单独讨论。超燃冲压发动机本身存在一系列气动弹性问题,包括壁板热颤振、激波振荡等问题,受于篇幅限制,本节不讨论发动机的气动弹性问题研究进展,而是着重总结气动弹性问题研究中发动机的建模研究工作。
超燃冲压发动机模型可以分为解析模型和数值模型,解析模型通过引入各类假设条件得到简单的参数表达式,在动力学建模时更具有优势。数值模型则保留了更多发动机特性,可以满足工程精度需要。
Chavez和Schmidt[4]先建立了一个低精度超燃冲压发动机模型,见图1。该模型包括扩散段、燃烧室以及内喷管三部分。建模中假设扩压段和喷管是等熵流动,通过总温的增加来模拟燃烧过程,可以给出推力随马赫数、高度、迎角、燃油当量比的变化关系式。该模型被广泛地应用于各类吸气式高超声速飞行器建模及仿真研究,为后续工压力分布的对比曲线见图4。从结果可以看出,该程序与试验结果趋势相符,但存在一定的误差,需要说明的是,计算中使用的常数项参数并未进行修正,在一定程度上验证了程序的通用性。MASIV在精度及效率上都可以满足一定的工程需求,已在气动弹性问题的研究上得到了一定的应用[10-11]。

图1 超燃冲压发动机解析模型[4]Fig.1 Scramjet engine analytical model[4]

图2 MASIV程序使用的发动机模型[6]Fig.2 Engine model used in MASIV[6]
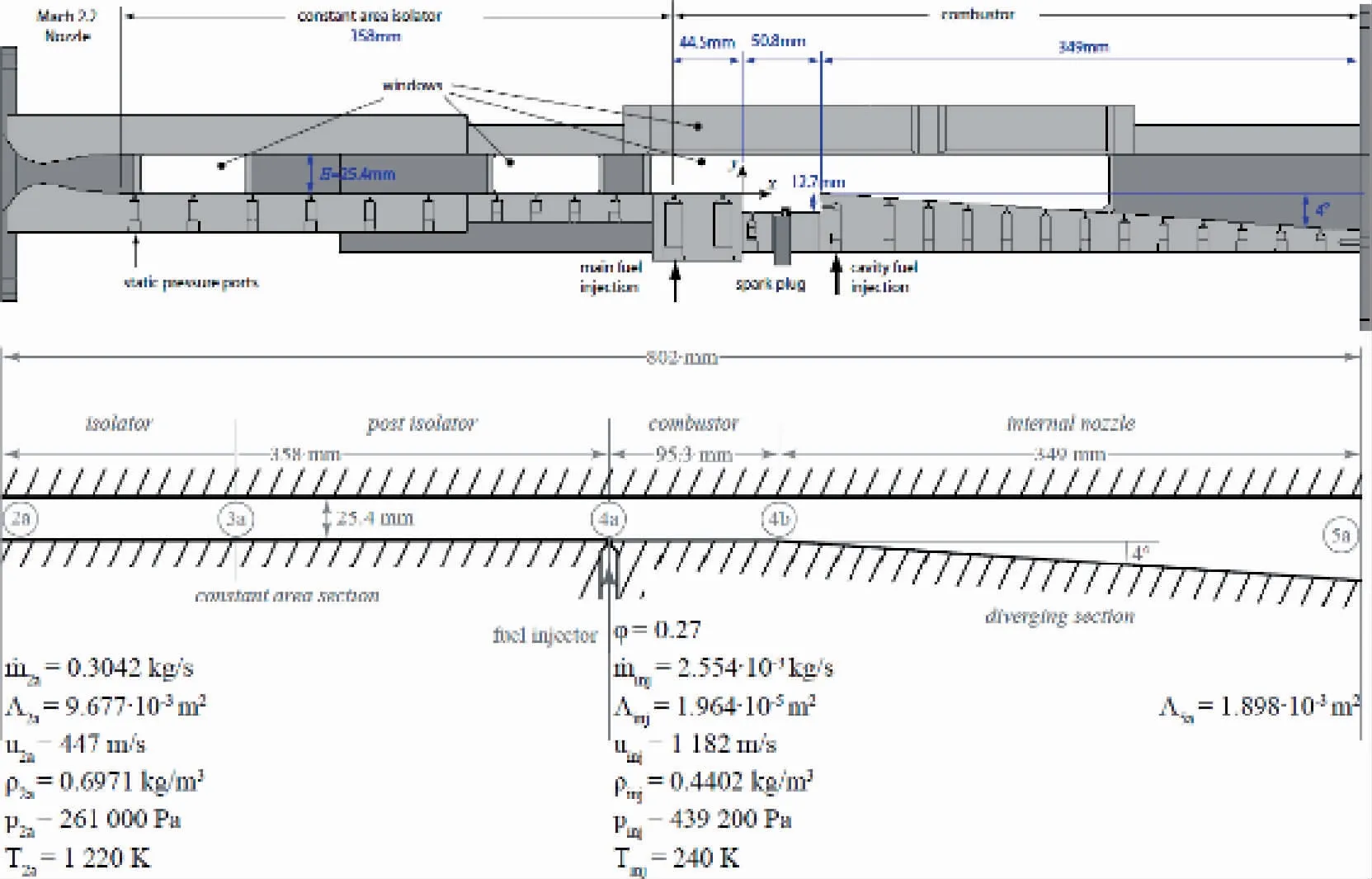
图3 试验装置示意图及MASIV程序计算模型[8]Fig.3 Experimental device schematic and MASIV calculation model[8]
SRGULL[12]程序通过求解二维欧拉无黏方程得到前体/进气道流场特性,利用边界层方程预测前体阻力及发动机入口参数,加上一维的燃烧室模型,共同分析整个推进系统流道。该程序可以考虑层流、过渡湍流边界层的影响,得到发动机流道的升力、推力、力矩,并可以模拟发动机不启动现象[13],同样得到了一定的应用[14]。
更高精度的三维发动机建模往往需要耗费巨大的计算时间,通过CFD方法以及燃烧相关软件CHEMKIN[15]等详细分析得到流场情况,并不适用于最初的设计阶段,此处不做过多介绍。

图4 压力分布结果对比[8]Fig.4 Comparison of pressure distribution results[8]
1.2 全飞行器一体化动力学建模
为了得到全机的飞行动力学、气动弹性动力学模型,在发动机建模的基础上,还需要考虑气动力、气动热、刚性/弹性结构以及飞行动力学建模。
对于高超声速飞行器单纯的气动力及气动热的建模问题,国内外许多学者进行了研究及总结[16],这部分并非本文的重点。目前高超热气动弹性领域常用的定常/非定常气动力及气动热计算方法,主要包括可与结构动力学耦合的CFD方法以及工程计算方法。而气动弹性中常用的工程方法,主要包括细长体理论、活塞理论[17]、当地活塞流方法[18]、牛顿冲击理论[19]等气动力计算方法,以及Eckert参考焓[20]、Spalding-Chi[21]等气动热计算方法。此外,对于吸气式高超声速飞行器,在气动力/热建模过程中,还需要对发动机的燃烧动力学问题进行一定的处理。
本节根据研究对象的不同,分别介绍二维及三维全飞行器一体化动力学建模情况。
1)二维模型
Chavez和Schmidt[4,22]建立了如图5所示的二维吸气式高超声速飞行器模型并进行了纵向动力学分析,模型建立过程中使用工程算法得到气动力,引入中间铰接梁模型来模拟弹性振动,如图6所示,随后推导得到了控制导数解析表达式,该经典模型至今被许多国内外学者使用。
Bolender和Doman[23]对 上 述 模 型 进 行 了 拓展,在气动力的计算中,使用斜激波/Prandtl-Meyer方法代替了原来的牛顿冲击方法。此外,添加了一个可平移的整流罩,用于在非设计条件下保持激波打在唇口状态,其几何模型见图7。

图5 飞行器几何外形[4]Fig.5 Vehicle geometry[4]

图6 弹性机体模型[4]Fig.6 Elastic vehicle model[4]
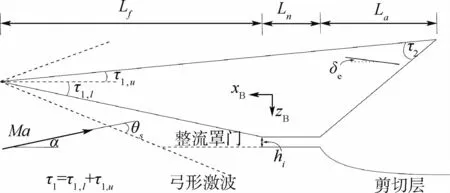
图7 吸气式高超声速飞行器几何模型[23]Fig.7 Geometric model of air-breathing hypersonic vehicle[23]
Williams等[24]重点考虑了飞行器质量变化及结构温度变化对整个飞行轨迹的影响,模型的内部体积示意图见图8,计算结果表明,飞行器模态的振型及频率主要由质量变化和加热效应主导。图9给出了飞行过程中第一阶模态演变情况,图中slugs为英制质量单位,1 ft=30.48 cm。随后的动图中力学计算发现,飞行器的短周期零极点随着燃料的消耗而移动,对系统的带宽产生了一定的限制,在建模过程中需要考虑上述2个因素的影响。
华如豪和叶正寅[25]建立了一个与图8类似的吸气式高超声速飞行器多学科耦合动力学模型,其中气动力及气动热分别使用工程方法得到,机体部分使用变截面梁来模拟,并考虑了燃油消耗的影响。随后在此模型基础上进行了静气动弹性配平以及动力学特征分析。
综上所述,二维模型的建模过程中,飞行器的几何外形多基于Chavez的构型,并添加不同的改进措施如鸭翼、发动机唇口控制、高精度发动机模型等;弹性的引入主要通过假设模态法,并根据考虑问题的不同进行不同精度的建模。
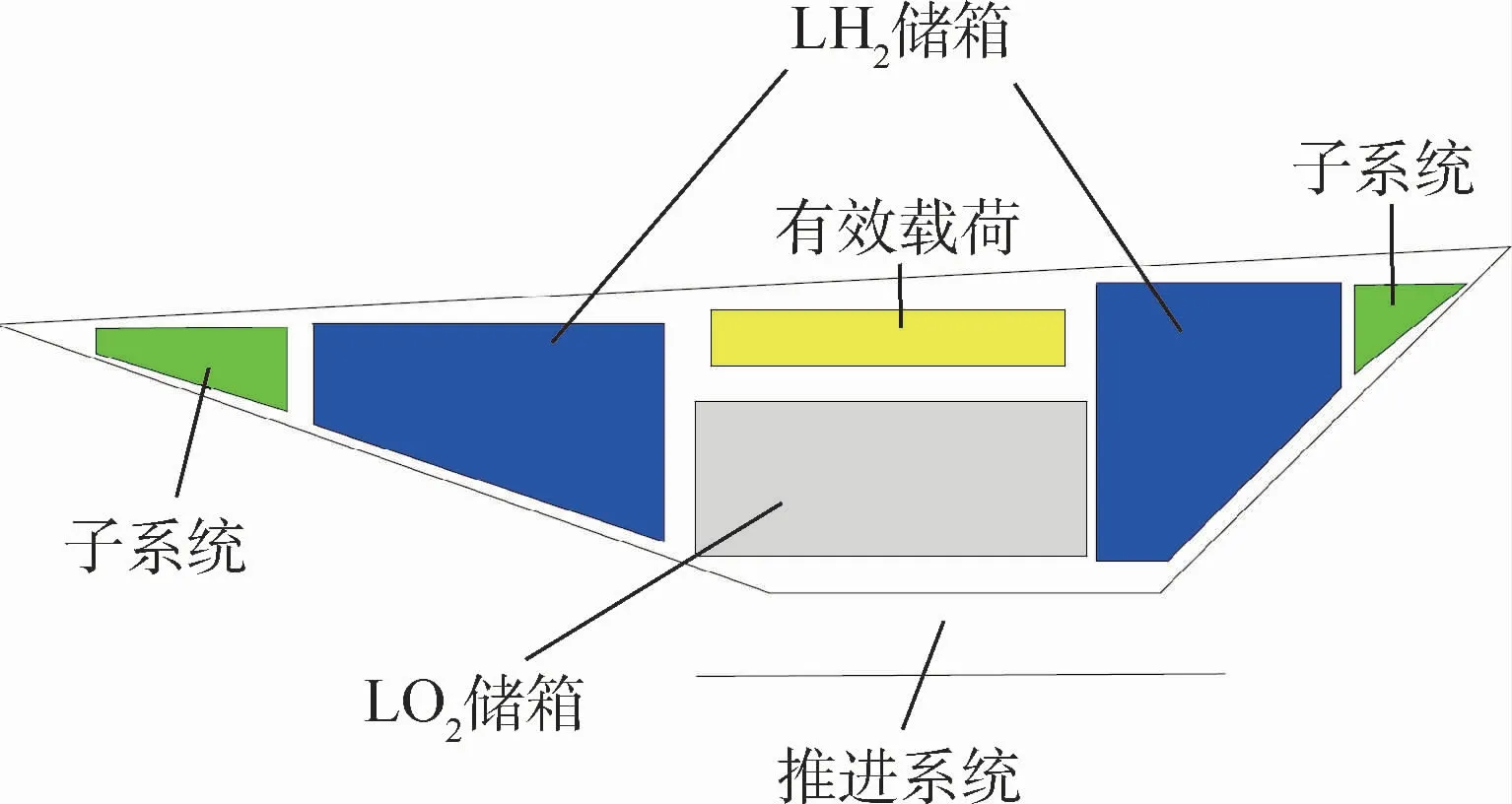
图8 内部体积分布示意图[24]Fig.8 Internal volume layout[24]
2)三维模型
Dalle等[11]建立了三维6自由度刚体模型,见图10。建模过程分为机体及发动机两部分,在保证了计算效率的同时保留了模型的高阶特征,可以很好地反映出机体/发动机的非线性耦合特征。
Sudalagunta等[26]建立了面向控制的吸气式高超声速飞行器气动弹性模型,见图11。对机体的刚性截面,使用6个独立位移来表示截面轴向、弯曲、剪切和扭转载荷引起的变形,推导出了弹性飞机的非线性运动方程。
在最近的文献中,Sachan和Padhi[27]对吸气式高超声速飞行器6自由度建模进行了简要的总结,并介绍了针对这些模型不确定性的鲁棒控制设计方法,提出了控制及建模未来可能的发展方向。
国内李惠峰等[28]使用三维外形参数化建模方法得到了飞行器几何模型,见图12。随后采用工程预估方法得到了气动力分布。发动机燃烧室的建模使用了简化的LH2燃烧模型。推导了刚体/弹性耦合矢量方程并使用拉格朗日方法建立了全机动力学模型。肖进等[29]同样使用参数化建模方法构建了三维模型,不同的是,气动力及气动热通过CFD方法得到,并进行了配平分析,具有一定的工程指导价值。

图10 高超声速飞行器等轴视图[11]Fig.10 Isometric view of hypersonic vehicle[11]

图11 典型的吸气式高超声速飞行器三视图(非比例绘图)[26]Fig.11 Three-sided view of a typical air-breathing hypersonic vehicle(figures not to scale)[26]

图12 吸气式高超声速飞行器三维视图[28]Fig.12 Air-breathing hypersonic vehicles 3D view[28]
2 吸气式高超声速飞行器热气动弹性动力学问题研究进展
吸气式高超声速飞行器由于涉及ASTEP多学科问题,因此不同问题的侧重点有所不同。本节从以下几个方面介绍相关问题的研究进展。
2.1 热气动弹性/推进耦合问题
Mcnamara和Friedmann[3]对高超声速气动弹性和热气动弹性问题进行了总结,从问题特征、建模方法、试验研究、热气动弹性相似律、壁板颤振、机翼和全机数值计算几个方面详细介绍了高超声速飞行器相关研究进展,随后指出了2个新的研究方向,其中之一便是热气动伺服弹性/推进耦合问题。文献[3]对吸气式高超声速飞行器部分的关注主要集中在动力学控制问题以及机体推进一体化多学科分析优化问题。
Chavez和Schmidt[4,22]对 某 二 维 模 型 进 行 了气动推进/气动弹性分析,建模过程参考第1节。分析时,首先计算了该模型的稳定性导数及控制导数,数值算例的结果表明,在某些情况下,发动机部分的影响可达到气动力的50%,且对全机稳定性导数造成不稳定贡献。随后的动力学模态分析表明,该模型在俯仰方向高度不稳定,具有显著的俯仰/弯曲耦合效应。飞行器气动力10%的变化将使其短周期频率发生34%的变化、弹性模态频率改变14%、弹性模态阻尼变化50%。同样,推力特性10%的变化将使其短周期频率发生11%的变化。证明了气动推进及气动弹性效应对全机动态特性都有显著的影响,因此需要整体建模方法。Schmidt[30]同样使用上述模型进行了纵向动力学特性分析,值得注意的是,其通过计算表明机身的俯仰运动将显著干扰燃烧室入口条件,且这些扰动的带宽与弹性固有频率一样高,需要对此进行有效的控制。
Raney等[14]对三维X-30类模型引入了七阶弹性弯曲模态加两阶刚体模态(俯仰及沉浮)进行分析,模型的模态及频率见图13。气动力计算使用牛顿冲击理论和二阶Van Dyke活塞理论的结合,发动机部分使用SRGULL代码。文献[14]研究了迎角和机体变形对于推进系统的影响,其中法向力随迎角的变化见图14,图中1 lb=453.592 37 g,实心符号表示无几何变形条件下的气动力数据,线段表示由湍流引起的几何变形条件下,气动力的变化范围,具有一定的工程参考价值。

图13 气动弹性模型中使用的结构模态振型及真空下频率[14]Fig.13 Structural mode shapes and in-vacuo frequencies used in aeroelastic model[14]
Rudd和Pines[31]研究了高超声速乘波体飞行器的动力学特性,气动力使用有限微分方法,并使用参考温度法计算阻力。结果表明,为了建立有效的控制系统,推进系统必须进行精确的建模。Mirmirani等[32]利用高精度CFD模型研究了一个全尺寸高超声速飞行器。首先在马赫数10,高度30 km条件下对二维模型进行分析,随后基于线性时变模型进行了控制系统研究[33]。Bolender和Doman[23,34]建 立 了 二 维 吸 气 式 高 超 声 速 飞 行的非线性模型,通过拉格朗日方程得到了弹性机体的运动方程,分析了线化系统的长短周期特性。
Culler等[35]以二维X-43为对象进行了气动及结构热力学分析,给出了燃油消耗及气动加热对于该模型模态以及飞行动力学特征的影响,相关结果分别见图15和图16。

图15 一阶弯曲模态的演变过程[35]Fig.15 Evolution of first-order bending mode[35]

图16 考虑气动加热和燃料消耗的系统极点/零点演变过程[35]Fig.16 Evolution of system poles/zeros considering aerodynamic heating and fuel consumption[35]
Klock和Cesnik[10]研究了吸气式高超声速飞行器热气动弹性仿真方法,建立了用于弹性高超声速飞行器的基于分区的、多物理场、多精度仿真框架,通过数值方法对比了分区求解与整体求解计算结果,两者吻合较好。
国内对热气动弹性/推进耦合问题也进行了一定的调研与研究。作者团队[2]对高超声速飞行器气动弹性力学研究进行了综述,介绍了气动推进/气动弹性耦合问题,从稳定性分析控制以及不确定性建模2个角度指出了需要关注的问题。向锦武等[36]针对典型吸气式高超声速飞行器构型研究了结构弹性对纵向静态特性和飞行动力学特性的影响。弹性模型采用弹性铰接的两段梁模型,分析了不同机体刚度对飞行配平参数以及动力学特性的影响。结果表明,全飞行包线可配平区域随着刚度下降而减小,见图17,其中ω1为机体第一阶弯曲频率,用于衡量机体弯曲刚度的大小。图18的动态特性分析结果指出,该模型短周期模态稳定性随着机体刚度的降低而下降,指出了将弹性因素引入该类飞行器分析中的必要性。

图17 不同机身弯曲刚度下的飞行包线[36]Fig.17 Flight envelopes under different bending stiffness of fuselage[36]
2.2 气动、结构、控制耦合
飞行控制系统的加入使得吸气式高超声速飞行器同样面临着气动伺服弹性问题,且推进系统的引入导致了全机控制系统设计更加复杂。针对该问题,国内外学者进行了一系列控制方法研究。
Fidan等[37]总结对比了相关文献中的吸气式高超声速飞行器控制系统设计方法,包括美国国家航空航天局(NASA)研究中心使用的控制方案。研究结果表明,吸气式高超声速飞行器控制面临的主要问题包括处理各种耦合效应、非线性、不确定性以及系统参数变化。后续的一个研究[33]基于时变模型进行了纵向运动学控制。
Parker等[38]基于Bolender和Doman[23]的高精度模型,通过力/力矩拟合,忽略弱耦合项等手段建立了一个面向控制的模型,可用于非线性控制系统的设计。文献[38]随后提出了基于近似反馈线性化方法的控制系统设计方案,仿真结果表明该方法即使在一定的参数扰动情况下,系统仍具有出色的跟踪性能。弹性效应的引入使得控制系统失效,在前体添加鸭翼可以用来补偿弹性效应的影响。Cui等[39]采用相同的建模思路进行研究,采用最小二乘法进行曲线拟合,面向控制的模型保留了原始真实模型的主要特性。
Dickeson等[40]开展了针对X-43构型的控制相关的建模/分析/设计研究,讨论了发动机及机体参数变化对系统静/动态特性的影响,同时揭示了控制系统设计时这些参数的影响机理。Sudalagunta等[26]在建立三维模型基础上,进行了系统开环稳定性分析,随后对线化系统进行了运动模态分析,并设计了线性二次调节器用于补偿初始条件的扰动。图19对比了开环和闭环条件下系统特征根分布,计算表明线性二次调节器可以满足系统的稳定性要求,并可通过参数调整使的系统最不稳定特征根更加远离虚轴。

图19 复平面中的特征值分布[26]Fig.19 Eigenvalue distribution in complex plane[26]
国内Duan和Li[41]、方洋旺等[42]分析了高超声速飞行器制导与控制问题的难点,并介绍了典型的线性/非线性控制方法。吴立刚[43]、王勇[44]等在此基础上针对吸气式高超声速飞行器的特点总结了控制系统的数学模型。
作者团队[45]利用二维吸气式高超声速飞行器模型,对机体/推进系统耦合下的气动伺服弹性问题进行了研究。结果表明,推进系统对飞行器的气动伺服弹性特性产生了显著的影响,考虑发动机控制系统的影响时,研究对象的气动伺服弹性稳定裕度下降约16%,在飞控系统的设计时需要考虑该因素。相关结果见图20,其中G、F分别为刚体失稳点以及气动伺服弹性失稳点,升降舵增益K取2.5时,系统临界失稳。
不同于系统的鲁棒性分析与设计,另一类研究主要针对机体/发动机整体控制[46-47],Schmidt和Velapoldi[48]将燃油当量比及扩散面积比作为发动机控制输入量,研究表明发动机指令对机体姿态产生了明显的扰动,指出了整体控制的必要性。Hao等[49]设计了一种机体/发动机的协调控制方案,该方法在不改变原始机体控制和发动机控制系统结构的基础上,通过引入发动机稳定裕度变量来调整原控制系统的参数,仿真结果表明协调控制方案保持了原系统的稳定性及速度指令跟踪能力,验证了其有效性。

图20 系统开环传递函数的Nyquist曲线对比(K=2.5)[45]Fig.20 Comparison of system open-loop transfer function Nyquist diagram when K=2.5[45]
2.3 吸气式高超声速飞行器的气动弹性强不确定性
吸气式高超声速飞行器的强不确定性特点,给气动弹性问题的研究带来了很大挑战。对于不确定性分析方法在气动弹性问题中的应用问题,文献[50]进行了详细的总结。在此基础上,吸气式高超声速飞行器的特殊设计构型带来了许多新的气动弹性不确定性问题,对此,国内外学者开展了一系列研究。
Buschek和Calise[51]针对一种吸气式高超声速飞行器模型进行了不确定性分析,将推力的变化以及机体的弹性振动分别作为不确定性来源,使用H∞和μ方法分析了控制系统的鲁棒特性。在此基础上对控制系统进行了降阶研究[52],并将降阶控制系统与全阶情况进行对比,验证了降阶的正确性。
Chavez和Schmidt[53]建立了非结构不确定性模型以及实参数结构不确定度模型,研究表明结构模态频率和阻尼的估计误差对系统的不确定性贡献较大。是否考虑弹性对系统不确定度产生了明显的影响,因此在控制律的设计时刚体假设可能不再适用。
作者团队[54]针对气动伺服弹性系统,采用结构奇异值方法分析了系统的鲁棒稳定性,该方法可以高效地建立弹性飞行器的状态空间方程,具有较强的工程应用价值。曲鑫等[55]将吸气式高超声速飞行器的不确定性来源归结为飞行器质量变化、压力分布误差等4个方面,进行了不确定性建模并设计了鲁棒协调控制器,仿真结果验证了该控制器的效果。曾开春和向锦武[56]在建立动力学模型的基础上,通过基于泰勒展开的区间分析方法(TIAM)和基于多项式逼近的区间分析方法(CIAM)研究了飞行动力学不确定性,并与直接蒙特卡罗(DMC)模拟方法进行对比。图21给出了2种计算方法得到的特征根不确定范围,结果表明,控制系统改变了不确定边界的形状及大小,同时,由于部分DMC模拟点落在了TIAM 边界之外而仍在CIAM 内,说明CIAM 在进行动力学不确定行分析时更加准确保守。
Pu等[57]从4个方面分别研究了吸气式高超声速飞行器模型的不确定性:弹性效应、气动参数、外部环境扰动以及建模误差。提出了鲁棒轨迹线性化控制(TLC)方案,仿真研究验证了鲁棒设计方案的良好控制性能和抗不确定性干扰能力。
2.4 相关试验研究进展
对于考虑吸气式超燃冲压发动机的气动弹性风洞试验无法也不大可能实现,目前考虑真实高空条件下的地面无发动机的高超热气弹试验也很难实现。
对于某些特定情况下的高超声速气动弹性风洞试验研究,美国开展的较早并取得了一些的成果[58-59]。国内目前在高超速风洞进行的气动弹性试验较少。季辰等[60-61]开展了针对舵、翼面的高超声速颤振试验研究,试验在中国航天空气动力技术研究院FD-07高超声速风洞中进行。试验装置见图22。该试验马赫数为5~6,通过应变片测量部件的振动信号,随后进行结构模态参数辨识以及亚临界颤振边界预测。
南京航空航天大学及合肥工业大学[62-63]共同开展了高超声速舵面的颤振试验,试验装置见图23。试验对象在29.5 kPa临界动压下发生了弯扭耦合颤振,颤振频率为29.3 Hz。数值仿真结果与该试验结果具有很好的一致性,并验证了模型限幅装置的安全性及有效性。

图21 纵向动力学模态复值特征根不确定范围[56]Fig.21 Complex eigenvalue uncertainty range of longitudinal dynamic modes[56]

图22 高超声速风洞中的翼面及颤振试验装置[60]Fig.22 Wing model and flutter testing apparatus in hypersonic wind tunnel[60]
受限于试验设备及实现难度,目前国内外尚未有针对吸气式高超声速飞行器模型完整的气动弹性试验,现有的试验主要为吸气式高超声速飞行器模型的气动力[64-67]、气动热试验[68]以及超燃冲压发动机相关试验[69]。
为了解决高速风洞气动弹性试验费用高、模型设备要求高等问题,国内外学者开展了许多关于半物理地面模拟加载气动力试验的研究。
目前模拟非定常气动力的加载方式主要为激振器离散点加载。作者团队[70]首先以细长体导弹为研究对象,对其气动伺服弹性问题进行了半物理地面模拟试验。试验装置见图24。在该装置基础上进行了系统开环响应以及闭环稳定性试验,数值仿真与实测数据一致性较好。
地面模拟试验的一个重要问题是如何有效使用较少的激振器更准确地模拟真实飞行条件下的气动力,并需要对激振器的位置进行优化选取。西北工业大学胡巍等[71]对地面试验中的气动力降阶方法进行了研究,使用二次降阶方法有效地减少了操纵面上激振点的个数,但是对于目前的试验能力,文中研究对象的激振器数量仍然偏多。

图23 试验模型与支撑机构[63]Fig.23 Test model and support mechanism[63]

图24 模拟气动力加载的导弹气动伺服弹性地面试验测试系统[70]Fig.24 Missile aeroservoelastic ground test system with simulated aerodynamic load[70]
其他的载荷加载方式还包括气囊加载系统[72]以及非接触式电磁加载[73]等方式,这些加载方式各有优点,但目前尚未得到广泛的应用。
3 结束语
吸气式高超声速飞行器作为一类特殊类型飞行器,其机体/发动机一体化构型、动力学问题刚弹耦合、强不确定性等特点,给该类飞行器的气动弹性的问题研究带来了新的挑战。本文回顾和总结了超燃冲压发动机及全飞行器动力学的建模方法及应用,在此基础上重点介绍了吸气式高超声速飞行器热气动弹性动力学问题的研究进展。从这些研究工作中得到的建议和结论主要包括:
1)发动机系统的建模与分析是吸气式高超声速飞行器气动弹性力学研究的重要问题之一。对于目前的发动机分析方法,一维方法精度过低,不能很好地反映发动机特性;三维方法通常需要考虑复杂的燃烧过程,计算量过大,实际应用困难,需要进行降阶处理;二维方法在精度和计算量上适中,比较适用于热气动特弹性力学问题,但应用时需要处理好三维机体模型和二维发动机模型之间不同维度的匹配问题。此外,发动机自身也存在控制系统,可能引入延迟环节,建议在开展热气动伺服弹性研究时考虑该因素的影响。
2)在研究吸气式高超声速飞行器热气动弹性力学及飞行动力学问题时,采用刚体假设将带来很大的误差,需采用刚弹耦合建模方法。此外,该类飞行器燃料质量系数大,机体频率在整个飞行包线过程中发生较大变化。同时,发动机工作时燃料质量消耗速率大,机体频率具有明显的时变性特点,该特点对热气动弹性问题的影响程度,目前尚不确定,仍需要进一步的研究。机体频率的变化将改变飞行配平参数,并影响系统的运动模态特征根分布,在某些情况下对飞行器的动力学稳定性造成不利影响。吸气式高超声速飞行器机体频率变化范围宽、变化速率大的特点,使得传统的滤波器不再适用,需要重新设计有效的控制系统。
3)高超声速飞行器面临复杂的飞行环境,不确定性分析将会成为重点问题。对于复杂非线性系统的不确定性问题,需要尽可能分析不确定性来源。在热气动弹性力学问题的分析中,研究人员对于结构和气动载荷的不确定性问题已有一定认识,未来应进一步考虑热不确定性问题的影响。热问题在时间上是累积过程,在与结构、气动问题共同计算时需要考虑各学科间时间尺度不同的问题。在空间上,热在不同方向的分布规律通常不同,因此在描述热不确定性问题时,时间和空间上的建模精度,将同时影响结果的准确性。
4)由于试验周期长、成本高且试验条件有限,目前数值仿真模拟仍然是研究该类飞行器的主要分析方法。常温条件下飞行器的气动特性试验较多,热环境下针对该类构型的试验虽然已经开展,但是仍然存在着许多不足。因此建议继续加强热气弹试验,设计适用于热环境下的测量采集试验装置,开发合理有效的热载荷加载方式,积累试验数据以便更好地理解热气动弹性力学机理;另一方面,地面模拟加载非定常气动力的气动弹性试验由于其成本低、模型尺寸不受限、安全性高等特点,在处理热气动弹性试验问题时具有特有的优势,有望成为一种有效的分析及试飞前验证的重要手段。
5)ASTEP综合问题是典型的多学科耦合问题,传统的热气动弹性力学处理耦合问题时,多将部分子学科进行解耦处理并/或忽略一些方向的弱耦合,推力通常为多场耦合动力学的外界输入条件。而对于吸气式高超声速飞行器,推进系统与其他学科的耦合将更加严重,往往不能解耦处理,因此需要多学科多场强耦合建模分析与计算方法研究;然而ASTEP耦合方法带来计算成本大幅增加,降阶方法可以提高计算效率,并保证一定的精度,因此也是处理多场耦合动力学问题的有效分析途径。

