Direct Application of Martin’s Axiom on Cardinal Invariants
ZHU Huiling, ZHENG Fudan
(1. School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510006, Guangdong;2. Three Gorges Mathematical Research Center, Three Gorges University, Yichang 443002, Hubei;3. Guangzhou College, South China University of Technology, Guangzhou 510800, Guangdong)
Abstract:In this paper, we study Martin’s Axiom and various forcing partial orders and explain how Martin’s Axiom can be directly applied to affect the value of the cardinal invariants of real number sets.
Keywords:Martin’s axiom; cardinal invariants; Cohen forcing; random forcing; local mathias forcing; Hechler forcing.
1 Introduction
In the modern era of set theory, forcing plays a significant role. Forcing was first developed by Cohen[1]to prove that Cantor’s continuum hypothesis is independent, in another word, unprovable from the usual axioms of set theory: the Zermelo-Fraenkel axiom system with the axiom of choice. Later, forcing was developed in depth by Solovay, Shelah, Woodin, Todorcevic, Magidor and many others. The reader is referred to Ref. Ref.[2] for the discovery of forcing, to Ref.[3] for the development of forcing, to Ref.[4] for elementary introduction to the techniques of forcing.
Forcing axioms acts as black boxes for the application of forcing. The first forcing axiom, Martin’s axiom, was formulated by Martin and Solovay[5]as by-product of investigation of internal forcing. Often, mathematicians from other fields, in particular, topology, care little about the details of forcing but care much about the effect of different forcing axioms.
There are many wonderful reference for Martin’s Axiom. For example, Ref.[6]. In particular, it was known that Martin’s Axiom trivialized almost all cardinal invariants. In this sense, this is not an open research problem. However, these results rely on the relationship among cardinal invariants. So it remains an open exposition problem. For each cardinal invariant, we attempt to find a forcing notion which can be directly applied in Martin’s Axiom.
Notations are standard. The reader is referred to Ref.[7-8] for the set theoretic terminology which are not explained in the paper. The rest of this article is organised as follows: Section 2 introduces Martin’s Axiom and Cohen forcing, Section 3 studies the cardinal invariants on the Baire space, Section 4 studies the cardinal invariants about the ideal of Lebesgue measure zero sets and first category sets. Section 5 studies the random forcing, Section 6 studies some properties of forcing which are stronger than the countable chain condition, Section 7 studies the local Mathias forcing, Section 8 studies the Hechler forcing, Section 9 discusses some problems for future study.
2 Background
In this section, we explain the background terminology which will be used throughout the paper.
2.1Martin’sAxiom
Martin’s Axiom, MA for short, is the following statement[5].
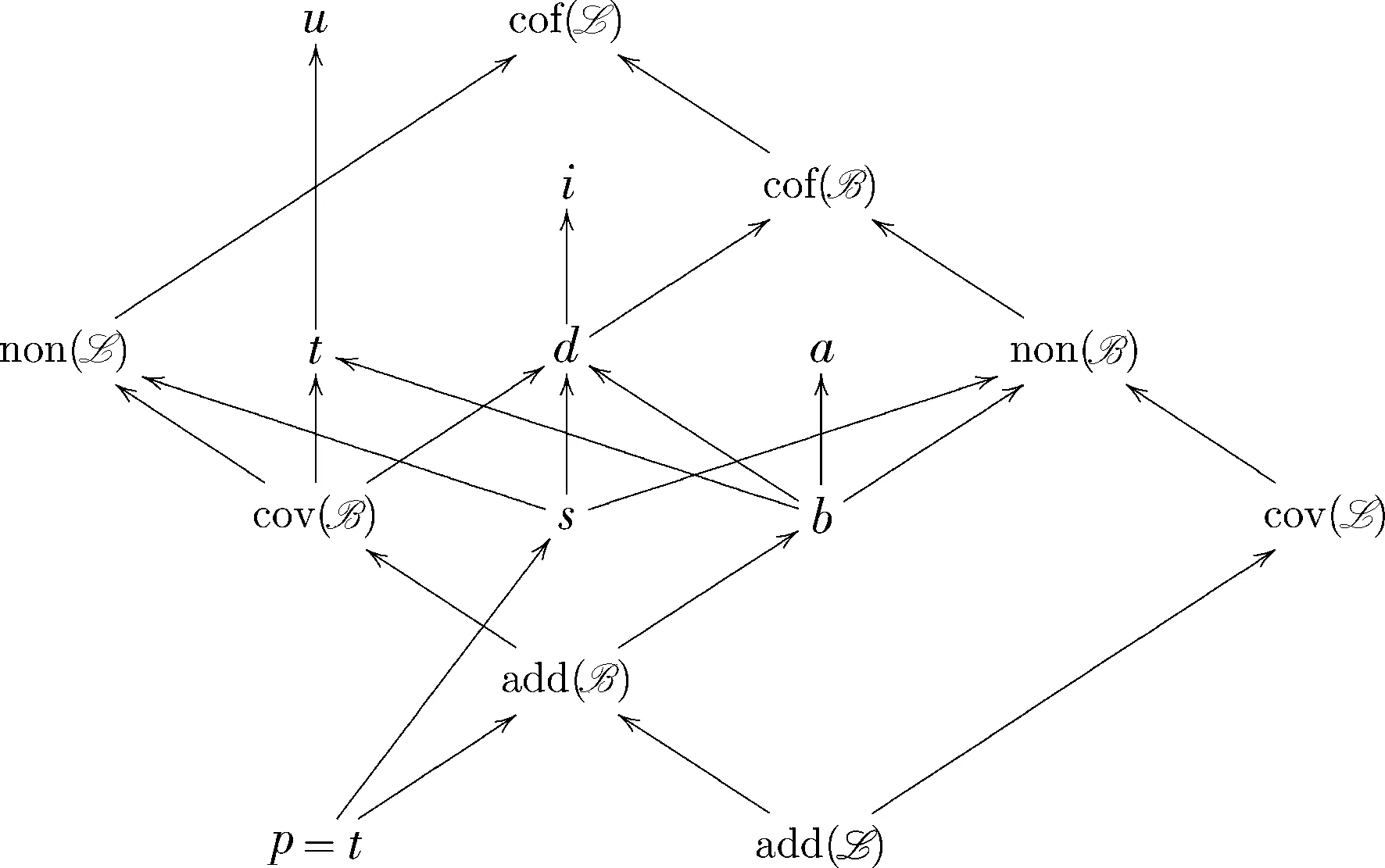
Definition2.1MAIf (P,≤) satisfies countable chain condition, and if D is a collection of dense subsets of P with |D| Here, (P,≤) is a partial order. To avoid triviality, the partial orders in practice will satisfy the forking requirement: ∀p∈P,∃q≤p,∃r≤psuch that there is nos, withs≤qands≤r. Usually, ifq≤p, we sayqis stronger thanp, orqis an extension ofp. Definition2.2We explain Definition 2.1 as follows: 1)A⊆P is an antichain, if ∀q,r∈A, eitherq=r, or there is nos, withs≤qands≤r. In other words, we sayAconsists of mutually incompatible elements. 2) (P,≤) satisfies countable chain condition, if any antichainA⊆P is countable. 3)D⊆P is a dense subset, if ∀p∈P∃q∈Dwithq≤p. 4) c is the continuum, namely the cardinality of the collection of reals. 5) ∅≠G⊆Pis a filter, if (p∈G∧p≤q)→q∈Gandp,q∈G→∃r∈G(r≤p∧r≤q). 6)G⊆P is D-generic filter, if ∀D∈D,G∩D≠∅. 2.2VariousCohenForcingCohen forcing is the most natural forcing to add a real. Cohen forcing is countable, and therefore has the countable chain condition. Since any two nontrivial countable forcing are equivalent(The reader is referred to Ref.[9] for the details of the fact), there is a variety of equivalent formulations of Cohen forcing. These formulation have the same logic strength in the sense that if one can solve a particular problem, then so can another. However, for a specific problem, we have to carefully select the right formulation so as to reduce the complexity of the presentation of the solution. 2.3CardinalInvariantsCardinal invariants, also called cardinal characteristics of the continuum, have been studied even before the age of forcing. The reader is referred to Ref.[10] for a survey on cardinal invariants. Research work on cardinal invariants are plentiful and are still active. Most notably, Ref.[11] proved the identity of two cardinal invariants p and t. In this section, we study four cardinal invariants: the dominating number d, the refining number r, the ultrafilter number u and the independence number i. We define each of the four and apply a variation of Cohen forcing to the equality with the continuum under the assumption of Martin’s Axiom. For each forcing, the generic object is on the Baire spaceωωor [ω]ω. 3.1Thedominatingnumber Definition3.1Define the dominating number as follows: 1) Forf,g∈ωω,fis dominated byg, if ∃m∈ω,∀n≥m,f(n)≤g(n). Denote this statement byf≤*g; 2) A family F⊆ωωis a dominating family, if ∀f∈ωω,∃g∈F,f≤*g; 3) The dominating number, denoted by d, is the least cardinality of a dominating family. Theorem3.2Martin’s Axiom implies d=c. ProofAssumeκ Dα,m={p|∃n∈dom(p),n>m,p(n)>fα(n)}. We show thatDα,mis dense. Givenq∈P, letn=max{m+1,dom(q)}, extendqtopsuch thatp(n)=fα(n)+1. Thenp≤qandp∈Dα,m. Similarly, forl∈ω, letEl={p|l∈dom(p)}. EachElis dense. By Martin’s Axiom, letGbe {Dα,m,El|α<κ,m<ω,l<ω}-generic. Letg=∪G. Theng∈ωω, andgis not dominated by anyfα. Hence d>κ, we conclude that d=c. 3.2Therefiningnumberandtheultrafilternumber Definition3.3Forp∈[ω]≤ω,q∈[ω]<ω, saypend extendsq, and denotep⊇eqif eitherp=q, orp⊃qandmin(pq)>max(q). Definition3.4Define the refining number and the ultrafilter number as follows: 1) SupposeA,B∈[ω]ω, sayBsplitsA, if bothA∩BandABare infinite; 2) A={Aα|α<κ}⊆[ω]ωis unsplittable, if for anyB, there is someAαnot split byB; 3) The refining number, r, is the least cardinality of an unsplittable family; 4) An ultrafilter base is some A={Aα|α<κ}⊆[ω]ωsuch that {X∈[ω]ω| ∃α,C⊇Aα} is an ultrafilter onω; 5) The ultrafilter number, u, is the least cardinality of an ultrafilter base. Lemma3.5An ultrafilter base is an unsplittable family, so u≥r. ProofLet A={Aα|α<κ} be an ultrafilter base. For anyB, there is anα, eitherB⊇Aα, orωB⊇Aα, soBdoes not split A. Theorem3.6Martin’s Axiom implies that r=u=c. ProofAssumeκ Let P=([ω]<ω,⊇e). Forα<κ,m<ω, letDα,m={p:|Aα∩p|>m},Eα,m={p:|(Aα∩max(p))p|>m}. These are dense subsets of P. For instance, we show thatEα,mis dense. Givenq∈P, sinceAαis infinite, leta0 By Martin’s Axiom, letGbe generic over these dense sets, and letg=∪G. Theng∈[ω]ωandgsplits eachAα. To see thatAαgis infinite, for anym<ω, letp∈Eα,m∩G, theng⊇ep. SoAαg⊇(Aα∩max(p),|Aαg|>m. 3.3Theindependencenunber Definition3.7Define the independence number as follows: 1) A family A={Aα|α<κ}⊆[ω]ωis an independent family, if for any finite family {α1,α2,…,αm;β1,β2,…,βn}∈[κ]m+n, is infinite. 2) An independent family is maximal, if it is not properly contained in any other independent family. 3) The independence number, denoted by i, is the least cardinality of a maximal independent family. Theorem3.8Martin’s Axiom implies that i=c. ProofAssumeκ Consider P=([ω]<ω,⊇e). For anyB, let DB,l={p∈P:|p∩B|>l∧|B∩(max(p)p)|>l}. Since A is independent, eachDB,lis dense. There are |κ<ω×κ<ω×ω|=κmany such dense subsets of P. By Martin’s Axiom, letGbe generic over these dense sets, and letg=∪G. Theng∈[ω]ωA and A ∪{g} is independent. Therefore, i >κ. Let B, L denote the collection of meager sets and null sets, respectively. In our applications, it does not matter which formulation of the reals is used. Both B and L areσ-ideals. Definition4.1For any ideal I, define four cardinal invariants about I: 1) The additivity of I, denoted byadd(I), is the least cardinality of some X⊆I, such that ∪X ∉I. 2) The uniformity of I, denoted bynon(I), is the least cardinality of someA⊆R, such thatA∉I. 3) A covering family from I is some X⊆I, such that ∪X=R. 4) The covering number for I, denoted bycov( I), is the least cardinality of a covering family from I. 5) A basis for I is some X ⊆I, such that ∀B∈I ,X∈X,B⊆X. 6) The cofinality of I, denoted bycof(I), is the least cardinality of a basis for I. It is easy to have the following. Lemma4.2If I is an ideal containing all singletons, thenadd(I)≤cov(I)≤cof(I) andadd(I)≤non(I)≤cof(I). 4.1Thecardinalinvariantsofthemeagerideal Theorem4.3Martin’s Axiom implies thatcov(B)=cof(B)=c. ProofAssume0≤κ ∀α<κ, letDα={p|p∩Xα=∅}. Givenq∈P,q° is an open interval and nonempty, sinceXαis nowhere dense, there is a nonempty open setΩ⊆q°,Ω∩Xα=∅. ∃p∈P,p⊆Ω. Sop∈Dαandp≤q. Hence, eachDαis dense. LetGbe {Dα|α<κ}-generic, and letg=∩G. Sincegis the intersection of a sequence of nested intervals,g≠∅. Butg∩∪=∅. So ∪≠R andcov(B)>κ. 4.2Thecardinalinvariantsofthenullideal Theorem4.4Martin’s Axiom implies thatnon(L)=cof(L)=c. ProofAssumeκ Consider the following partial order P: a conditionpis a union of open intervals with rational endpoints andμ(p)<, whereμdenotes the Lebesgue measure;p≤qiffp⊇q. P is countable, and is a form of Cohen forcing. For eachα,Dα={p|yα∈p} is dense. By Martin’s Axiom, letGbe generic over these dense sets andg=∪G. ThenY⊆gandgis an open set. To complete the proof, we show thatμ(g)≤. Since P is countable,g=∪i<ωpi, with eachpi∈G. By definition, ∀l<ω,∪i≤lpiis a lower bound forp0,p1,…,pl, soμ(∪i≤lpi)<. Therefore,μ(g)≤. Remark4.5The partial order above is closely related to the amoeba forcing, which is used to prove a stronger statement:MAadd(L)=c [5]. It was more complicated to check the countable chain condition there. We explained how Cohen forcing can be adopted for the application of Martin’s Axiom on cardinal invariants of the real line. However, the power of Martin’s Axiom can not be fully demonstrated by countable forcing. Moreover, the generic objects added by Cohen forcing have certain properties which preserves the value of some cardinal invariants. For instance, as the Cohen real is not dominating over the ground model, the unbounding number remains the same. We have to move on to find uncountable partial orders which have countable chain condition. Fortunately, there are many such forcing partial order, as we will see in the following sections. The random forcing[12]P consists of Borel sets with positive measure,p≤qiffp⊆q. To simplify notation, we consider the interval (0,1) instead of R. Recall thatμdenotes the Lebesgue measure. Lemma5.1Random forcing satisfies countable chain condition. ProofIfX⊆P is an antichain, then ∀p,q∈X, eitherp=q, orp∩q=∅. LetXn={p∈X:μ(p)>1/n}. Since the measure of (0,1) is 1,Xnhas less thannelements. Therefore,X=∪n<ωXnis countable. For eachn<ω, consider a partition: whereZnis a finite set of rationals. Theorem5.2Martin’s Axiom implies thatcov(L)=c. ProofAssumeκ LetGbe generic overDα’s andEn’s, and letrgbe the random real decided byG.G∩Dα≠∅ guarantees thatrg∉Aα, sorg∉∪A. Therefore,cov(L)>κ. In this section, we investigate some properties which help to verify the countable chain condition. Then we can apply Martin’s Axiom to forcing satisfying these properties. Definition6.1Given a forcing P and a subsetW: 1)Wis linked, if every two elements ofWare compatible; 2)Wis centered, if any finite many elements fromWhas a common lower bound; 3) P isσ-linked, if P=∪i<ωWi, eachWiis linked; 4) P isσ-centered, if P=∪i<ωWi, eachWiis centered. Lemma6.2Anyσ-centered forcing isσ-linked; anyσ-linked forcing has the countable chain condition. ProofThe first statement is obviously true. To prove the second, letA⊆Pbe an antichain, then for eachi,A∩Wihas at most one element. SoAis countable. The local Mathias forcing was used to prove p=c underMA. Details can be found in Ref.[10]. We adopt it here to decide the cardinal invariants t, s and a. 7.1Definitionandproperties Definition7.1A family A⊆[ω]ωhas strong finite intersection property, if for any nonempty F⊆A, ∩ F is infinite. This forcing is called the local Mathias forcing (with respect to A). The original Mathias forcing (The reader is referred to Ref.[13-14] for the details) has nothing to do with A; it requires only thatSis infinite. The stronger intersection property of A guarantees that P has countable chain condition. Lemma7.2P isσ-linked. (In fact, P isσ-centered.) ProofGiven (s,S) and (s,S′), (s,S∩S′) is a condition and is a common extension of them. So the forcing P can be partitioned into countable many pieces, conditions in the same piece have the sames. Definition7.3DenoteX⊆*YifXYis finite. Theorem7.4Martin’s Axiom implies that if A={Aα|α<κ} has strong finite intersection property andκ ProofDefine the local Mathias forcing as above, forα<κ, letDα={(s,S)|Aα⊇S}.Dαis dense. Similarly,En={(s,S):|s|>n} is dense for eachn<ω. By Martin’s Axiom, letGbe generic over theseDα’s andEn’s. Letg=∪{s|∃S, (s,S)∈G}.G∩Enimplies that |g|>n, sogis infinite. Fixα, let (s,S)∈Dα∩G, thenS⊆Aα. We show thatgs⊆S. Ifm∈gs, thenm∈s′ for some (s′,S′)∈G. With out loss of generality, we may assume that (s′,S′)≤(s,S). Thenm∈s′s⊆S. Therefore,gs⊆Aα. 7.2Applications Now we apply the local Mathias forcing to the almost disjointness number a, the tower number t and the splitting number s. Definition7.5Define the almost disjointness number as follows: 1)X,Y∈[ω]ωare almost disjoint, ifX∩Yis finite. 2) An almost disjoint family is some A={Aα|α<κ}⊆[ω]ω, such that any two members are almost disjoint. 3) A maximal almost disjoint family is an almost disjoint family A such that any A′⊃A is not almost disjoint. 4) The almost disjointness number, denoted by a, is the least cardinality of a maximal almost disjoint family. Lemma7.6If A={Aα|α<κ} is an almost disjoint family, then A′={ωAα|α<κ} has strong finite intersection property. Corollary7.7Martin’s Axiom implies that a=c. ProofLet A={Aα|α<κ} be an almost disjoint family, whereκ Definition7.8Define the tower number as follows: 1) A tower is a sequence T=〈Tα:α<γ〉 from [ω]ω, such that ifα<β<γ, thenTβ⊆*Tα. 2) A tower Tis extendible, if there is some tower T′ which properly extends |T|. 3) The tower number, denoted by t, is the least cardinality of a tower which is not extendible. Lemma7.9A tower has strong finite intersection property. ProofLetα1<α2<…<αn<γ. ThenTαn⊆*Tαifor 1≤i is infinite. Corollary7.10Martin’s Axiom implies that t=c. ProofGiven a tower T=〈Tα:α<γ〉 , whereγ Definition7.11Define the splitting number as follows: 1) A splitting family is some A={Aα|α<κ}⊆[ω]ωsuch that for anyB∈[ω]ω, there is someAαwhich splitsB, namely that bothB∩AαandBAαare infinite. 2) The splitting number, denoted by s, is the least cardinality of a splitting family. The following lemma shows that a splitting family will be converted into an unextendible tower with the same length. As a corollary, Martin’s Axiom implies that s=c. Lemma7.12t≤s. ProofGiven a family A={Aα|α<κ}, withκ Hechler forcing[15]is also called dominating forcing, which adds a dominating real in a natural way. 8.1DefinitionandpropertiesHechler forcing P consists of pairs (h,H), whereh∈ω<ω,H∈ωωandHagree withhon the domain ofh. (h′,H′)≤(h,H) ifh′ end extendsh, ∀l∈ω,H′(l)≥H(l) and ∀l∈dom(h′)dom(h),h′(l)≥H(l). Lemma8.1Hechler forcing satisfies countable chain condition. ProofActually, it isσ-centered, for our purpose, we show that it is isσ-linked.P can be divided into countable many piece, each piece has the sameh. Now (h,H) and (h,H′) have a common lower bound (h,max(H,H′)), wheremax(H,H′) is defined pointwisely. 8.2TheunboundingnumberDefine the unbounding number: 1) A family F ⊆ωωis an unbounded family, if ∀g∈ωω∃f∈Ff≤/*g. 2) The unbounding number, denoted by b, is the least cardinality of an unbounded family. Theorem8.3Martin’s Axiom implies that b=c. ProofSuppose F={fα|α<κ} withκ As a result, we can show the following: Corollary8.4Martin’s Axiom implies thatnon(B)=c. Many cardinal invariants have been involved in previous sections, for the purpose of future study, we record known results on connections between cardinal invariants in the following diagram: It was proved in Ref.[5] thatadd(L)=c by applying amoeba forcing in Martin’s Axiom, are there alternative forcing for this statement It was proved in Ref.[16] that by a two-step iteration of Hechler forcing, Martin’s Axiom is able to show thatadd(B)=c. Is there a natural way to prove this statement? What are the correct forcing for the cardinal invariants h, g and e? Is it possible to develop a classification theory of cardinal invariants for the applications of Martin’s Axiom, or other forcing axioms? 接受日期:2018-12-203 Reals on the Baire space
4 The meager ideal and the null ideal
5 Random forcing

6 Stronger properties
7 Local Mathias forcing


8 Hechler Forcing

9 Discussion