高温作业专用服装设计

邱秀亮 俞青清 杨位乾 陈旭

摘   要：本文基于傅立叶定律结合多层平壁热传递模型和干燥热传递模型，构造时间—位置—温度的热传递偏微分方程来解决热防护服装厚度的合理设计问题，然后将偏微分方程进行离散化处理，通过数据预处理发现皮肤表层超过1646s以后温度不再增长，我们认为自此系统处于动态热平衡状态。利用有限差分法在MATLAB上算出动态热平衡之前的温度分布，得到动态热平衡状态时各层交界处的温度。

关键词：热防护服  干燥热传递模型  有限差分法

中图分类号：TS941.2                               文献标识码：A                        文章编号：1674-098X（2019）05（c）-0082-02

现如今人们从事各种高温作业下的安全隐患有增加的趋势，在高温条件下热防护服具备对人体進行安全防护的功能而显得十分重要。比如消防员在火场环境灭火救援时常处于高温高辐射的环境，如果防护服太厚重，经常会导致热应激反应，因此在高温作业时保护人体皮肤不受伤害的前提下，如何减少防护服厚度，是本文讨论的根本问题。

目前急需要解决的问题有：（1）根据已知的服装材料的参数值以及在条件为75℃环境温度、II层厚度为6mm、IV层厚度为5mm、工作时间为90min的情形下，计算温度的分布;（2）当环境温度为65℃时，IV层厚度为5.5mm时，在确保工作60min时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5min的条件下确定II层最优厚度;（3）当环境温度为80℃时，在保证工作30min时，其余条件与上述相同以此来确定II层和IV层的最优厚度。

1  模型的建立与求解

1.1 建立模型

傅立叶定律是通过归纳大量实验结果建立起来的，导热的基本模型如下[1]：

1.3 模型求解

有限差分法[8]数值计算的基本步骤[9]：

（1）区域的离散或子区域的划分;

（2）插值函数的选择;

（3）方程组的建立;

（4）方程组的求解。

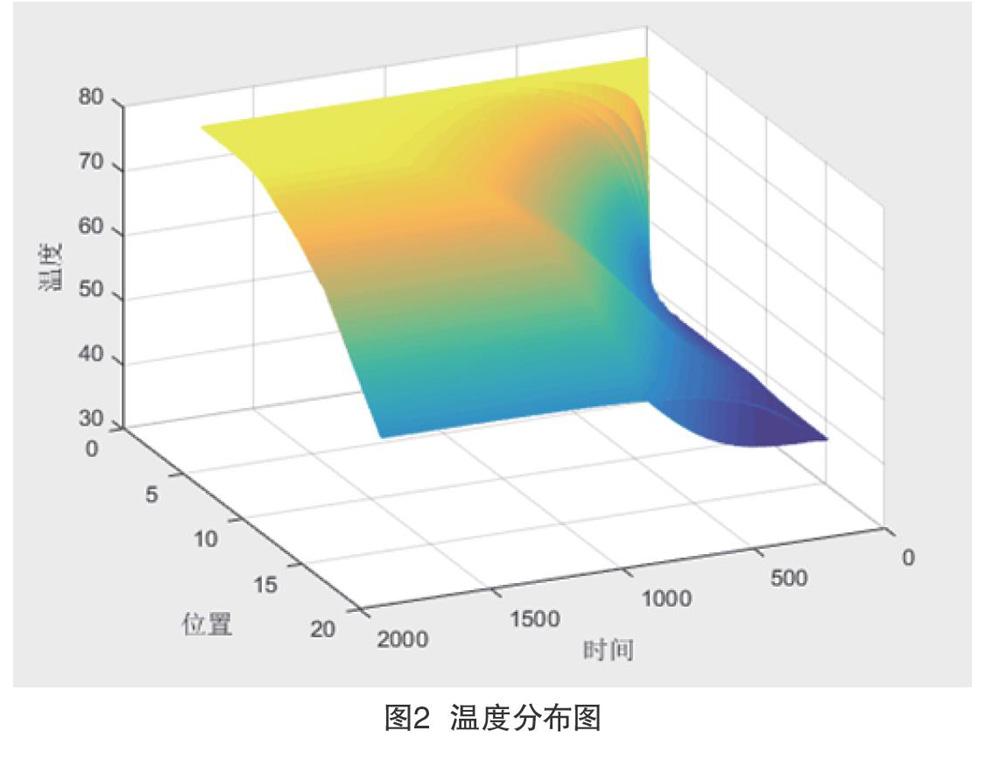
通过matlab绘制出的温度分布如图2所示。

1.4 Ⅱ层的最优厚度

利用问题一的偏微分方程，建立假人皮肤外侧温度与第Ⅱ层厚度和时间的关系。由于第Ⅱ层厚度在0.6～25mm之间，以0.1mm间隔遍历出最优厚度范围在9.2～9.3mm之间，继续细分得到第Ⅱ层最优厚度9.232mm。

1.5 Ⅱ层和Ⅳ层的最优厚度

构造皮肤外侧温度与第Ⅱ层和第Ⅳ层的厚度以及时间的关系T（l2，l4，t），双重循环遍历出最优厚度。得到第Ⅱ层最优厚度为8.7mm，第Ⅳ层最优厚度为6.1mm。

2  模型的评价与优化

2.1 模型的优点

建立的模型能与实际紧密联系，具有坚实可靠的数学基础，所需数据少，可操作性强。

2.2 模型的缺点

（1）考虑的影响因素较少，处理问题时可能存在一些误差;

（2）涉及许多数学以及物理公式，计算量较大。

2.3 模型的优化

用BP神经网络预测模型建立织物的物理性能与热防护性能指标之间的关系，输入向量为外层织物的厚度、面密度、组织结构、经密、纬密、紧度、导热系数、极限氧指数、损毁长度共9个性能指标，输出向量为织物的TPP值，来建立消防服用外层织物的热防护性能预测模型。并进行模型预测能力的验证。

参考文献

[1] 范治新.工程传热原理[M].北京：化学工业出版社，1982.

[2] 李淑芬.计算机软件技术基础[M].北京：机械工业出版社，2013.

[3] 卢琳珍.多层热防护服装的热传递模型及参数最优决定[D].浙江理工大学，2018.

[4] 田苗，李俊.数值模拟在热防护服装性能测评中的应用[J].纺织学报，2015，36（1）：1-6.

[5] 卢琳珍，徐定华，徐映红.应用三层热防护服热传递改进模型的皮肤烧伤度预测[J].纺织学报，2018，39（1）：1-8.

[6] 杨杰.基于人体-服装-环境的高温人体热反应模拟与实验研究[D].工程物理系、核科学与技术，2016.

[7] Fan J T， Luo Z X，Li Y.Heat and moisture transfer with sorption and condensation in porous clothing assemblies and numerical simulation[J].International Journal of Heat and Mass Transfer，2000（43）：2989-2000.

[8] G.W.Song，R.Barker and H.Hamouda.Modeling the thermal protective performance of heat resistant garments in flash fire seposures[J].Textile Research Journal，2004，74（12）：1033-40.

[9] 史策.热传导方程有限差分法的MATLAB实现[J].咸阳师范学院学报，2009，24（4）：1.