找准“概念胚胎”的生长点——以《分数的初步认识》为例

安 蕾

一、课前思考：“分数的初步认识”在教材编排体系中身居何位？

在小学阶段，“分数的初步认识”的教学建立在整数知识和平均分知识的基础之上，是学生与分数的第一次接触。从整数到分数，对学生来讲不仅是知识面的拓展，更是数概念的一次扩充。当前，教材将分数的各种定义分散在各个年级完成，却始终没有明确告知学生：分数是一个数。

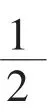
于是，我们思考：站在学生的角度，“分数的初步认识”到底该认识到哪？对于一个概念的“胚胎”而言，它将是后继学习的重要生长点。

二、课中慎思：站在学生的角度，寻找“概念胚胎”的生长点

1.寻找衔接概念经验的生长点。

学生学习新知的时候，如果这个新知是与原来经验吻合的，那么学生就容易接受，反之，如果需要另起炉灶，学生的学习就会相对慢一些。那么，关于分数的初步认识，学生的已有认数经验是什么？学习新知的生长点在哪里？显然，学生在自然数学习中积累的数学活动经验是学习新知的最佳经验生长点。

师：把4 个月饼平均分成2 份，每份是几个？

生：每份是2 个。

师：每份分得同样多就是平均分。这2 个是4 个月饼的？是几个？

生：把4 个月饼，平均分成2 份，每份是它的一半，是2 个。

师：我们用“2”来记录分得的结果。现在有2 个月饼，平均分成2 份，每份是它的多少？是几个？

生：把2 个月饼，平均分成2 份，每份是它的一半，是1 个。

师：我们用“1”来记录分得的结果。如果把1 个月饼平均分成2 份呢？

生：把1 个月饼，平均分成2 份，每份是它的一半，是半个。

师：这半个还能用以前的1、2、3 这样的数来表示吗？

生：不行了。

师：那么，半个可以用一个怎样的数来表示呢？

生：0.5。

师：为什么想到0.5，你在哪里见过它？

生：报纸上，超市里……

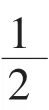
在生活中，学生对物体的“一半”并不陌生，所以将教学的起点建立在“一半”的生活经验基础上，通过“分月饼”找到4 个月饼的“一半”是2 个，2 个月饼的“一半”是1 个，1 个月饼的“一半”是半个。这样的引入，将“经验”与“数学”衔接，“半个”不能用1、2、3……这样的数来表示，需要引入一种新的数表示事物的量，如此，引发认知冲突，让学生感知“分数”产生的实际意义。

这样的教学过程与自然数的学习相吻合，当学生完成内在的数学活动经验衔接后，也就意味着找到了学习分数的“最佳经验生长点”。

2.寻找凸显概念本质的生长点。

分数强调的是部分与整体的关系，如何凸显分数这个概念本质，找到一个最佳生长点？只有将抽象概念与学生已有知识经验建立有层次的联系：引导学生在概念的抽象定义、半抽象模型、具体活动之间寻找意义与数学化的过程，他们才能把握分数本质。

师：我们能不能用一个图形来表示我们要分的物体？

生：正方形、长方形、圆……

生：因为我们都把一个圆平均分成了2 份。

生1：一半。

生：因为是把正方形竖着对折了。

师：把正方形对折也就是把它平均分成了——

生：平均分成2 份。

学生举出下图中的例子。

生：因为都是把正方形进行对折，也就将正方形平均分成了2 份。

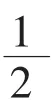
3.寻找深化概念理解的生长点。

要完整准确地把握分数这个概念的本质，最终还是要让其转化成一个对象，即“分数本身是一个数”，要让学生体会分数是可以数的，分数是有大有小的。

片段三：积累经验、深化认知（数一数分数）

师：通过刚才的学习，我们知道了分数是一种数，它可以数，下面就让我们一起数一数吧。

师：竖着看，你发现了什么？

师：你是怎么看出来的呢？

生：我是通过观察图形。

师：你能给它们排排队吗？

师：继续想，你还能想到几分之一？大小怎么样？

…………

师：也就是说，平均分成的份数越多，每一份就越——

生齐呼：越小。

师：我们再横着看，你发现了什么？

师：（课件演示）受此启发，你还想到了什么呢？

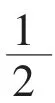
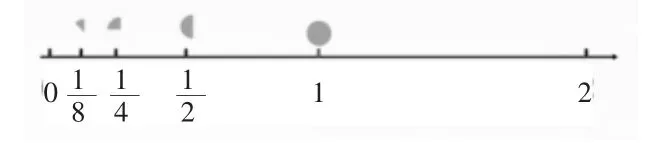
生指，课件演示。

通过数形结合“数一数”，将自然数的数数经验迁移，初步感知，分数也是数单位的累积。将分数通过数形结合数一数，并落到数轴上，充分体现了分数作为数的本质属性，学生的思维得到了进一步的发展。再结合“比一比”“找一找”将分数纳入“数”的知识体系中。最后，学以致用，把生活融于数学，把知识融于生活，体会数学的应用价值。

三、课后反思：“初步认识”还能走得更深更远

张奠宙教授在文章中曾对“分数的初步认识”这一知识点的教学提出两点改进建议：首先要从问题驱动入手，明确为什么要学习分数，并且明白分数是有大小的数；其次是在分数的认识学习历程中应该对分数的大小有适当的描述，这样在比较分数大小时才不显得突兀。笔者在教学中依据这两点建议从学生的角度找准“概念胚胎”的生长点，引导学生一起研究分数的来龙去脉和本质属性。这样的教学，学生对概念的理解不再是单向封闭的，他们会触类旁通地联想与延伸，从而使概念学习走得更深更远。