一种基于网格地图的双A*算法的改进方法
袁川涵
【摘 要】随着科技的发展和技术的提升,机器人在现代社会中的应用越发广泛。在机器人路径规划问题中,传统的Dijkstra和A*算法为带来了在运算速度方面的诸多便利。但是Dijkstra和 A*算法也有着运行效率偏低,找到最优解的准确率不高,路径距离计算不精确等诸多问题。本文提出了基于双A*算法的直线和曲线替代的方法,对在传统网格地图上的路径问题就行了综合的分析与算法上的改进。在不提高算法计算复杂度的前提下,提升了机器人路径规划的空间距离的优化和系统处理的效率,同时节省了处理过程的内存占用。
【关键词】路径规划;空间距离;双A*算法
中图分类号: TP18;TP242文献标识码: A 文章编号: 2095-2457(2019)29-0148-002
DOI:10.19694/j.cnki.issn2095-2457.2019.29.069
0 概述
随着现代科技的发展,人类生活愈发依赖机器人的协作和辅助,机器人路径规划问题成为当前研究的重要方向。人力成本的节约和机器人自身的效率的高低成了判定机器人是否实用的重要指标。在机器人路径规划问题的众多解决方法中,工程师们通常采取的是以Dijkstra算法为基础的A*算法来解决机器人路径问题,但是A*算法自身的局限性和单一性,导致在一些特殊情况中,A*算法求解出的最短路径往往不是最优解,并且具有占用系统内存高,时间耗费大等缺点。故在本文中我们讨论了针对A*算法进行了的优化,并提出了一种新的最短路径方法,能够在减少其响应时间的同时使路径变得更平滑,该优化方法相对于传统的A*算法在效率得到了显著的提升。
1 背景知识/算法介绍
1.1 Dijkstra算法
Dijkstra(迪杰斯特拉算法)算法是由荷兰计算机科学家提出来以贪婪算法为基础的,解决从单点到其余各点的最短路径的计算方法,其主要解决的是有向图的最短路径问题。Dijkstra算法的核心是某个顶点出发向外拓展遍历相邻所有顶点,找到最短解后再进行下一轮的遍历,直至到達所以目标顶点。该算法虽然能得出最短路径的最优解,但是它要计算所有点之间的路径,导致运算效率偏低。Dijkstra算法的具体思路是,采用贪婪策略,建立一个数组Dis来保存起始点到各个顶点的最短距离,然后在建立一个集合T来保存已经找到最短路径的各个顶点。首先,原点A的路径权重被赋为0(Dis(a)=0)。若对于顶点s存在能直接到达的边(a,m),则把Dis(a)设为W(a,m),同时把所有其他顶点的路径长度设为无穷大。当程序开始时集合T只有顶点a。然后,从Dis数组选择最小值,则该值就是源点a到该顶点的最短路径,并且把该点加入到T中。再加入第一个顶点之后,需要判断此顶点是否能够到达其他顶点以及是否比从起点直接到其他顶点路径更短,如果判断有更优解,则保存更优解,再从Dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
1.2 A*算法
A*算法是建立在Dijkstra算法基础上的一种启发式搜索算法,根据一定的启发函数,求解最优路径。其启发函数为
f(n)等于g(n)加h(n)(1)
其中:
f(n)为起始点与节点以及终点的代价函数,g(n)为起点到当前点的最短路径的实际代价值,h(n)为当前点到终点的估计代价值。
在整个函数中起关键性作用是h(n),其决定了A*算法运算效率的高低。如果h(n)为0,那么只是g(n)在式中发挥作用,则A*算法就变为了Dijkstra算法,因此当h(n)变小,则运算量变大导致运行速率降低。若h(n)小于节点到终点的真实代价,那么此刻A*算法依旧能够寻找最短路径目的。若h(n)等于节点到终点的真实代价,则A*算法可以达到更快寻找路径且不向外扩张以此得到效率最大化。若大于或远远大于节点到终点的代价,g(n)基本不发挥作用,则A*算法就会变成BFS(Best-First Search)算法。
A*算法相比于Dijkstra算法,能极大地提高搜索效率与检索速度,并且极大地减少了搜索的区域。但是传统的A*算法由于其搜索速度缓慢,内存占用大等缺点,故在自动寻路问题中,工程师一般采用双A*算法来解决问题。
1.3 双A*算法
由于A*算法的搜索方式属于单向递进搜索,即运行每一步都在选取最优解,当所有的最优解组合在一起则会形成最终的最优路径。双A*算法的基本思想是在起始点和终点出发,沿着正反两个方向同时通过A*算法搜寻路线,当各自方向上拓展出相同的最优节点时停止搜索。其具体步骤如下:
(1)创建两个open和两个close表,open表存储正反方向的拓展点信息,初始和终点也包含在内。
(2)找出各自open表内f(n)最小值select,并存进各自close表格内,并以此点为父节点拓展子节点,其子节点放入open表内。
(3)判断两个select点是否满足终止条件,如不满足则继续进行(2)步骤,如满足则停止程序并遍历父节点存入result表作为最终路径。
尽管A*算法对比Dijkstra等传统算法的时候具有运算效率高,内存占用率低,运行速度快等优点。但是A*算法在面对复杂地形的问题时,特别是起点宽阔和终点被复杂的障碍物包裹的地图,A*算法会自动寻找到离终点最接近的点,但是在寻路过程中因为障碍物无法穿透导致路径围绕障碍物一圈直至到达终点。在此情况中,双A*算法则更加具有实用性。双A*算法在继承了A*算法所有的优点的同时,增加了准确性和寻路效率,减少了运算时间。
2 改进算法
在实际解决问题中,网格地图会经常出现连续折线路径和大量直角转弯的情况。此情况中机器人路径选择缺乏灵活性,且会增加路径的长度和烦琐程度。因此本文在基于双A*算法的基础上,采用直线替代法和短边曲线替代法,以及面对折线过渡直角转弯的特殊情况下,两种方法互相配合以达到最大程度节省路径的目的。
直线替代:本文采用直线替代和短边曲线的方式来进行双A*算法的优化。直线替代法是在路径中出现连续折线,同时检测是否存在障碍物。则系统自动判定优化条件,在连续折线的情况下由连续折线的首端到连续折线的末端画一条直线,以此来作为新的路径。
短边曲线:短边曲线替代法是在路径遇到直角转弯这种情况,且两边长度a和b不同。则通过以短边为半径画圆,其弧线作为路径以便平滑地度过直角。
折线过渡直角转弯:本文着重探讨由折线到直角转弯的过渡情况,这种情况通常以一条短边连续向不同的方向转弯两次。因此会有不同的情况以及优化方案。详细的解决方案在本文的实验分析部分进行详细阐述。
3 实验分析
本文使用边长为1的正方形网格地图来进行测试分析。在连续折线的情况下,通常采用在起点和终点连接一条直线来节省路径。以一个正方形为例,正常情况下机器人寻路程序采取折线法,改进后采取直线替代法由正方形的左上角画一条直线到右下角。网格地图每一边的边长为1,所以折线法的总路程为2。而直线替代法能够有效地将路径长度降低为1.141。相比原始方法降低了42.95%,且随着折线数量的变长,能够节省同样比值的路径,大大地提高小车的工作效率和运算速度。
在直角转弯的情况下,通常寻路程序采取笔直的沿着两条直角边為路径,改进后,以短直角边为半径的弧线作为小车的行驶路线。同样以网格地图为例,两条直角边长度为1,2。以1为半径画弧线,这一条弧线的长度为0.785,改进前的总长度为3,改进后为1.785。相比改进前,路径节省了40.5%。
在直角边长度为2和3时,通过计算得出弧线长度约为3.14,总长度为4.14,相比变长为1和2时,效率降低但仍有一定的节省路径。
但在短边长度大于3的时,此法不具有实用性。通过计算得出,在两边长度为3和4时,总路程为7。而使用短边曲线替代法的时候,总路程为8.065。因此当短边长度大于3的时候,我们采取直线替代法。通过计算得出直线替代法的总路程为5.24,相比原始路径减少了25.1%的路径。
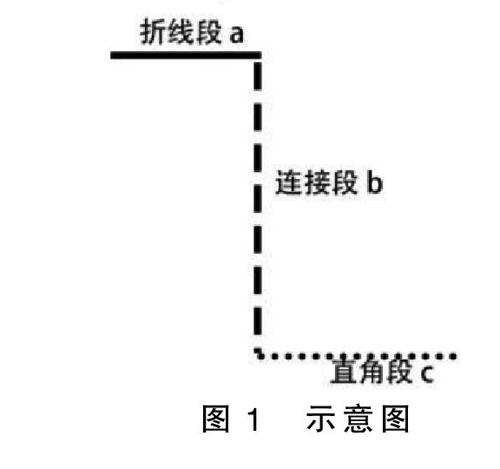
图1 示意图
在连续折线转直角边的特殊情况下,小车的路径问题通常需要考虑几种不同的条件。我们以下图为例,折线边的长度为a,连接段的长度为b,直角段的长度为c。
(1)b大于6。
我们直接采取连接的方式,从连续线段的起点直至线段的终点。
(2)b小于或者等于6,a小于或者等于二分之一个b,b小于或者等于二分之一个b,我们采取短的那条边的长度为半径画弧线。
(3)b小于6,a等于二分之一个b,b等于二分之一个b,我们采取直接画弧线,半径为任意一边的长度。
(4)b小于6,a大于或者等于二分之一个b,b大于或者等于二分之一个b,我们采取以中间线段的1/2为半径向两边画弧线。
(5)b小于或者等于6,a小于或者等于二分之一个b,b大于或者等于二分之一个b或者a大于或者等于二分之一个b,b小于或者等于二分之一个b,我们采取让短边这一侧用短边长度为半径画弧线,而长边则使用中间线段与短边之差的长度为半径画弧线。
4 结论
本文主要研究了在经典网格地图中的路径问题,提出了基于双A*算法的改进方法,在最短路径算法中,使用直线和曲线进行替代,解决传统路径所导致的路径距离过长的问题。通过对地图上空间距离的计算和对多种情况的具体分心,给出了改进方法在路径规划上应用的具体方案,使算法能够得到最优解,让小车的路径变得更加平滑和灵活。通过针对不同的路径情况给出的不同规划策略,使得在复杂的路径问题能够快速地找出最佳路径。
本文实验和算法都是基于传统的A*算法及其扩展,后续将结合智能算法进一步在效率和性能上进行提升。

