含体积型缺陷管道的剩余强度分析

张足斌 王婷婷 焦震

1中国石油大学（华东）山东省油气储运安全省级重点实验室

2中国石油青海油田分公司采油二厂

在我国，随着能源结构的不断优化，“西气东输”“海气登陆”等重大项目正在建设或实施中，大量油气输送管道形成了贯通大江南北、连接海内外的管网，极大地促进了我国经济的发展和国际地位的提高。因此，管道运输作为最为主要的能源运输方式，运输过程中的安全问题得到了广泛的重视。我国油气管道材料以钢管为主，且90%以上管线采用埋地敷设的方式，经过长期运输使用，管道老化严重，加上运输介质的腐蚀现象和施工过程中的不当操作，管道面临风险较多。一旦发生管道泄漏或爆炸，往往会造成火灾、中毒灾难性事故[1]。

剩余强度是判断油气管道可靠性的重要指标，因此各国先后颁布了相关的评价标准[2-4]，如ASME B31G 准则、修正的ASME B31G 准则、API 579、DNV-RP-F101等。这些方法具有一定的可行性，但是与实际情况仍存在一定的偏差，其评价结果较为保守。有限元法是一种高效可靠的评价方法，郭茶秀等[5]对含有裂纹缺陷的直管在复杂组合载荷工况下进行有限元模拟，得到了相对应的极限载荷，对裂纹管的研究起到了较大的推动作用。沈士明等[6-7]采用正交实验设计方法，利用有限元软件对组合载荷作用下的管道进行模拟研究，得出对应的极限载荷，并在此基础上总结出了求解临界工作载荷近似值的方法。张旭昀等[8]使用ANSYS 软件对缺陷长度、宽度和深度等参数不同的含缺陷管道进行模拟计算，得到了管道的剩余强度，分析了平底方形和椭圆形等缺陷不同的模型对失效压力的影响。因此，对于现场的实际问题，应用有限元方法可以得到准确的评价结果。

本文使用ABAQUS软件，建立含体积型缺陷管道的有限元模型，分析缺陷参数变化对管道剩余强度的影响规律，并将响应曲面法与有限元分析相结合，回归出相应的方程，讨论各因素间的相互作用。

1 研究方法

1.1 非线性有限元法

以某气田的实际数据为例，选用的直管段几何尺寸为外径D=0.508 m，设计壁厚t=0.022 2 m，根据圣维南原理，设定管段长度为L=2 m。材料参数依据L360MCS 直缝埋弧焊钢管特性，弹性模量E=210 GPa，泊松比ν=0.3，屈服强度σs=358 MPa，材料服从各向同性和小变形假设。考虑到几何非线性和材料非线性，选用式（1）中Ramberg-Osgood[9]本构模型表示材料的应力、应变关系。

本文主要研究对象为含体积型缺陷的直管段，为贴合实际情况，将缺陷形状简化为三轴不等的椭球体，并通过改变缺陷的长度、宽度、深度和长轴夹角来研究缺陷参数对剩余强度的影响。含单缺陷直管结构如图1所示。

图1 含单缺陷直管示意图Fig.1 Straight pipe with single defect

使用ABAQUS软件建立有限元模型时，重点研究区域为缺陷区域及其周边。为了确保结果的准确性并节省时间，进行网格划分时，将缺陷区域切割成一个单独的部分，再采用自由网格中的C3D10单元对该缺陷区域进行细密划分，而其余区域选用C3D20R 单元进行粗略划分，模型单元总数为174 815左右。划分网格后的管道模型如图2所示。

图2 含缺陷管段网格划分示意图Fig.2 Schematic diagram of grid division of pipe with defects

在不同的工况下，应使用不同的约束条件。因研究对象为埋地管段，考虑到周边土壤的固定效果，所以在管段一端施加六自由度全固定约束，另一端不施加约束。由于研究对象地处山区，管道经过高低起伏较大的地段时，周围土壤可能会发生塌陷，产生弯矩的作用。在模拟过程中，在管道内壁面施加法向压力，同时在自由端创建mpc184单元节点，以构建刚性梁的方式来施加100 kN·m 的弯矩载荷。考虑到由内压引起的轴向作用，需要在弯管的自由端施加一个等效轴向拉应力。

在对含体积型缺陷管道进行分析时，需要建立屈服条件。含体积型缺陷管道是否发生失效，可以通过缺陷区的Von Mises 等效应力来判断。由于L360钢材为低级钢，采用应力失效准则，当缺陷区域最深处沿厚度方向上的Von Mises 应力达到一定的参考值，当参考应力σref=σs（即管道屈服强度）时，管道判定为失效。Von Mises 条件假设是当最大形状改变比能到达极值时，开始发生屈服。单元体的三个主应力按大小顺序分别为σ1、σ2、σ3，其条件表达式为

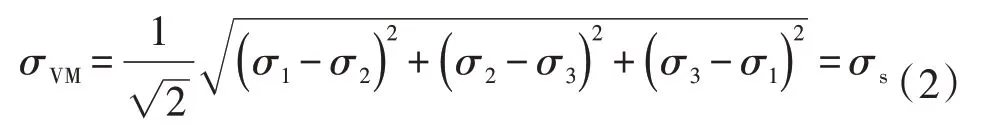
1.2 响应曲面法

响应曲面法[10]适用于需要对非线性数据进行处理的情况，包括实验设计、模型建立、模型校验及显著性分析等步骤。在实验与分析中，通常回归方程的格式为

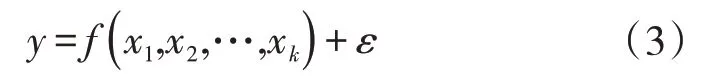
式中：x1、x2,…,xk为自变量，即影响反应值的独立变量；ε为反应变量的误差，通常认为ε服从常态分配且相互间独立，其期望值为0；y为因变量，即受影响的反应值。

在数据收集完之后，一般会通过最小平方法将其回归成一阶线性模型，以确定一个较为适当的函数，回归式为

根据自变量与因变量之间的关系强弱，来判断确定的函数是否合适，若不合适，则应考虑二阶模式，其数学表达式为

按照Box-Behnken 型响应曲面法的设计要求，设计了四因素三水平共27组实验点的分析实验。把缺陷的长度、宽度、深度和长轴夹角四个几何参数作为自变量，管道的剩余强度设为因变量，每个模型的中心点数为3。实验因素和水平的选值如表1所示。

表1 实验因素及取值水平Tab.1 Experiment factors and numeric value

2 结果与分析

2.1 缺陷参数变化时的有限元结果

取体积型缺陷的长、宽、深分别为40、16、8 mm，改变其长轴与管道轴线的夹角，在管道受100 kN·m 弯矩载荷的作用下，对其增大内压直至失效，剩余强度与长轴夹角之间的关系见图3。

图3 长轴夹角变化时的剩余强度Fig.3 Residual strength when the angle between long axis changes

从图3可以看出，长轴夹角逐渐变大时，管道的剩余强度相应地增大，从17.5 MPa 增大到30.9 MPa，增大了76.57%。从断裂力学的角度考虑，可能是因为当长轴夹角变大时，缺陷投影到轴剖面的轴向长度变短，投影到横截面的环向长度变长。初始时，缺陷区域等效应力同时受到长度和宽度尺寸变化的影响，因此变化效果较为明显。而在长轴夹角较大时，投影后的长度尺寸较小，而宽度尺寸较大，尺寸的变化已不能引起较大的应力变化，此时等效应力的变化趋势越来越小，故剩余强度的变化也变得平缓。

取体积型缺陷的宽度和深度分别为16和8 mm，改变其长度，在管道受100 kN·m 弯矩载荷的作用下，对其增大内压直至失效，剩余强度与缺陷长度之间的关系见图4。

图4 长度变化时的剩余强度Fig.4 Residual strength when the length changes

从图4可以看出，在缺陷长度尺寸逐渐增大的过程中，管道缺陷区域的剩余强度呈减小的趋势，且减小的幅度越来越小，曲线最后趋于一个定值，管道的可靠性越来越低。长轴夹角变大时，剩余强度随缺陷长度变化的曲线变得平缓。特别是当长轴夹角为0°、长度为10 mm时，由于宽度取为16 mm，从断裂力学的角度考虑，缺陷投影到轴剖面的轴向长度小于投影到横截面的环向长度。而当长轴夹角变为60°时，投影后的轴向长度大于环向长度，所以长度为10 mm 的缺陷在长轴夹角变大时，其剩余强度不升反降。

取体积型缺陷的长度和深度分别为40和8 mm，改变其宽度，在管道受100 kN·m 弯矩载荷的作用下，对其增大内压直至失效，剩余强度与缺陷宽度之间的关系见图5。从图5可以看出，当缺陷的长度和深度一定时，其宽度尺寸的变化对剩余强度有显著的影响。在缺陷宽度尺寸逐渐增大的过程中，管道缺陷区域的剩余强度呈增大的趋势，且增大的幅度越来越小；在宽度尺寸大于20 mm 时，曲线趋于平缓。总的来说，缺陷宽度变化所引起的剩余强度变化比长度变化所造成的影响要小很多。

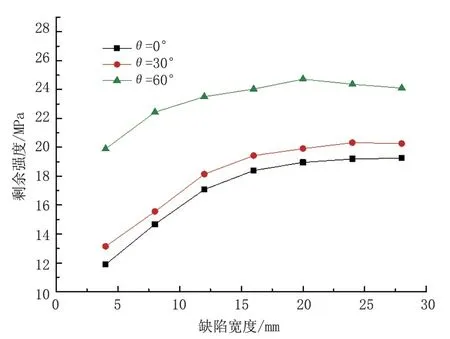
图5 宽度变化时的剩余强度Fig.5 Residual strength when the width changes

取体积型缺陷的长度和宽度分别为40和16 mm，改变其深度，在管道受100 kN·m 弯矩载荷的作用下，对其增大内压直至失效，剩余强度与缺陷深度之间的关系见图6。

从图6可以看出，在缺陷深度尺寸逐渐增大的过程中，管道缺陷区域的剩余强度呈减小的趋势。当长轴夹角变大时，剩余强度曲线下降的坡度变得平缓。总的来说，缺陷深度变化所引起的剩余强度变化比宽度变化所造成的影响要大一些。

2.2 响应方程的建立及显著性分析

根据响应曲面法的设计要求，通过ABAQUS求出27组实验点的值，模拟结果如表2所示。

根据线性模型拟合出线性方程表达式为

根据2FI 模型拟合成的二次交互项方程如式（7）所示

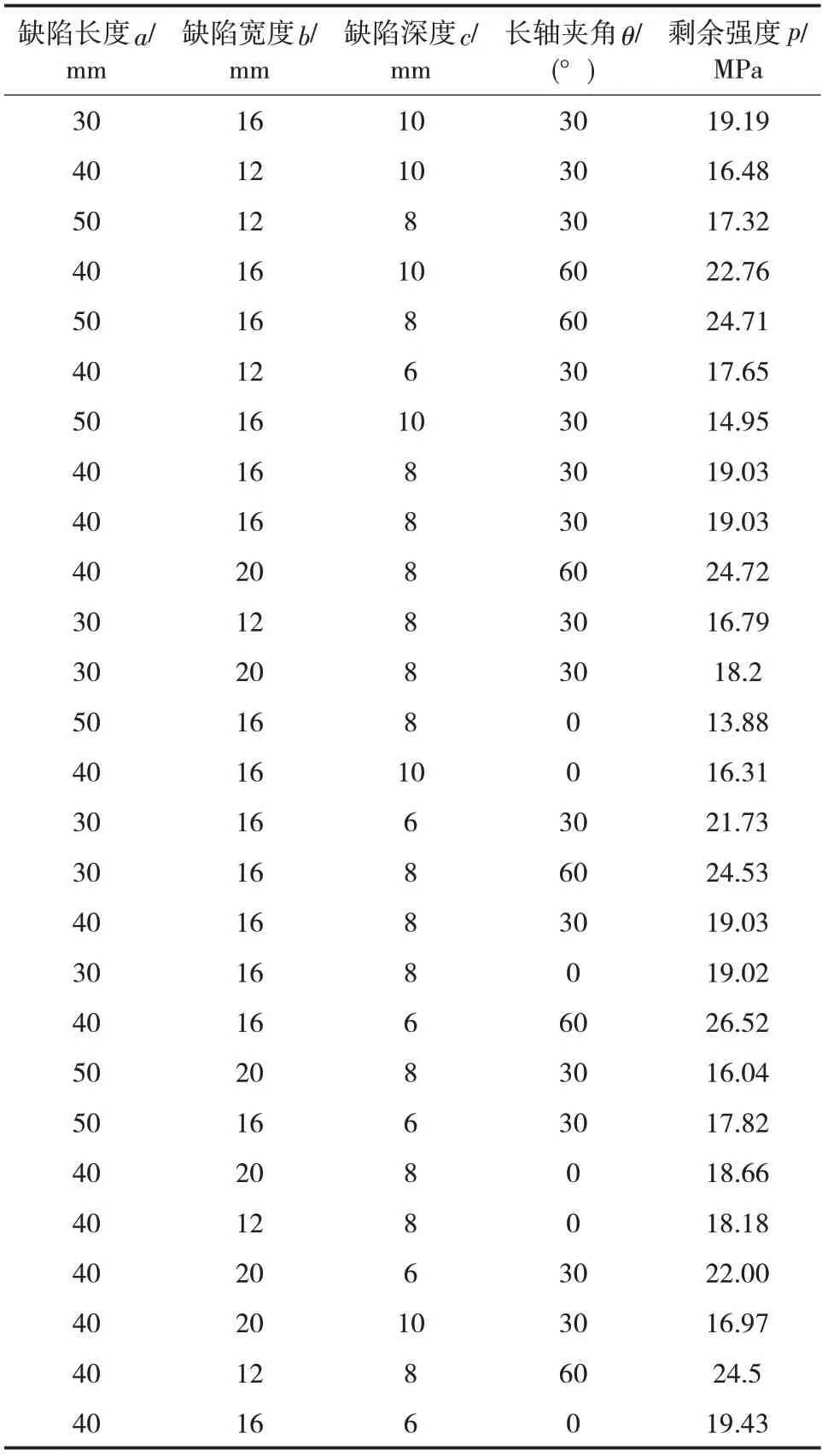
表2 实验设计及结果Tab.2 Experimental design and results

根据二阶模型拟合成的二次多项式方程表达式为

从表3中模型的方差分析可以看出，利用二阶模型拟合实验数据效果较好，P模型＜0.01，说明失拟误差并不显著；其校正决定系数r2为0.952 8，说明仅有不到5%的变异情况不能由此模型来表示，在这三个拟合的模型中，二次多项式模型的拟合度最好。

表3 多种模型分析比较Tab.3 Analysis and comparison of different models

由表4的方差分析可知，就单因素而言，缺陷宽度的影响不显著，其他三个因素的显著性大小关系为：长轴夹角 ＞缺陷深度 ＞缺陷长度。由拟合公式中的回归系数，可以得出缺陷参数对剩余强度的影响。当缺陷长度和深度增大时，含缺陷管道的剩余强度逐渐减小；当缺陷宽度增大时，含缺陷管道的剩余强度变化较小，仅略有增加；当长轴夹角增大时，含缺陷管道的剩余强度逐渐增大，且增大速率较快。这一结论与前文的分析基本一致，因此可以认为本模型的建立是准确的。

表4 二次模型的方差分析Tab.4 Variance analysis of quadratic model

对各因素间的交互作用进行分析可知，ac的P值为0.049 8，aθ的P值为0.028 2，均小于0.05，说明缺陷长度a和缺陷深度c、缺陷长度a和长轴夹角θ的交互影响较为显著，而其他因素间的交互作用对含缺陷管道的剩余强度并没有起到较大的影响。在缺陷深度和长轴夹角一定的情况下，随着缺陷长度的增加，管道的剩余强度也减小，且下降速率较快。各因素显著性所讨论的结果和前文的分析结果一致。

3 结论与建议

以受内压和弯矩联合作用下的含体积型缺陷直管段为分析对象，对其剩余强度进行了分析。针对分析结果，提出以下结论和建议：

（1）在影响含缺陷管道剩余强度的缺陷参数中，就单因素而言，长轴夹角、缺陷深度、缺陷长度的影响效果比较显著，而缺陷宽度的影响较小；就交互作用而言，缺陷长度和缺陷深度、缺陷长度和长轴夹角的影响较为显著。

（2）应用响应曲面法在管道剩余强度研究中回归出精度较高的二次模型，建立了管道剩余强度与各缺陷参数的关系方程。该方法所需实验次数较少，同时全面考虑了各个因素及其之间的交互关系。

（3）后续可对含多个缺陷的直管段进行研究，以增强分析的全面性。