不同干扰程度下土壤有机质空间最优插值法研究
马利芳,熊黑钢,孙 迪,王 宁,叶红云,张 芳
1 新疆大学资源与环境科学学院,绿洲生态教育部重点实验室, 乌鲁木齐 830046 2 北京联合大学应用文理学院, 北京 100083
有机质是土壤必不可少的组成成分,是土壤质量及肥力评价的基础,在土壤发挥功能与碳循环过程中起重要作用[1-2]。明确有机质的空间分布特征是土壤资源与环境科学管理的依据[3-4]。近些年,人类活动所造成的干扰对地表自然状况及生态环境的影响不断加剧[5],不同程度的人为干扰对土壤有机质空间分布的影响有所差异,这在有机质十分匮乏的干旱区更加明显。因此,对干旱区不同人为干扰程度下土壤有机质含量进行空间插值研究,对掌握土壤有机质的空间分布规律以及实现干旱地区农业可持续发展意义重大[6]。
当前,国内外已有大量关于土壤属性空间插值的研究,地统计方法尤其是克里格插值法的应用相对广泛[7-8]。例如:利用普通克里格法分析了克什米尔农业区[9]、尼罗河三角洲地区[10]、意大利耕地和牧场[11]、北京某生态功能区[12]、典型喀斯特峰丛洼地小流域[13]内土壤属性的空间分布特征等,但亦有研究显示普通克里格法并不能够很好地对土壤有机质进行插值分析[14]。与传统的克里格法相比,采用改进土地利用回归法[15]、随机森林法[16]、地理加权法[17]等方法或者借助辅助变量[18]对土壤属性进行空间分布特征分析,会实现提高空间插值精度的目的。已有关于土壤属性空间插值方法精度比较的研究,结论并不一致[19-20],能够适用于所有土壤属性,且精度在任何区域都达到最优的插值方法并不能被确定。现有研究结果最终选择的最优空间插值方法相差迥异。例如,有学者认为径向基函数法能更好地表达土壤属性的空间分布特征[21];亦有研究采用不同插值方法对土壤属性插值精度进行比较,发现反距离加权法的估算效果更佳[22]。还有相关研究表明不同土层深度的有机质含量最优插值方法也有所差异[23]。
现有成果可能是在不同土壤环境背景下的讨论,故有较大的差异。因而,利用反距离加权法、径向基函数法和局部多项式法对不同人类干扰程度下的土壤有机质空间特征进行研究,探讨不同空间插值方法对其估算精度的影响,以期寻求不同人类干扰下土壤有机质的最优空间插值方法,为提高空间估测精度提供价值参考。
1 材料与方法
1.1 研究区概况及样点布设
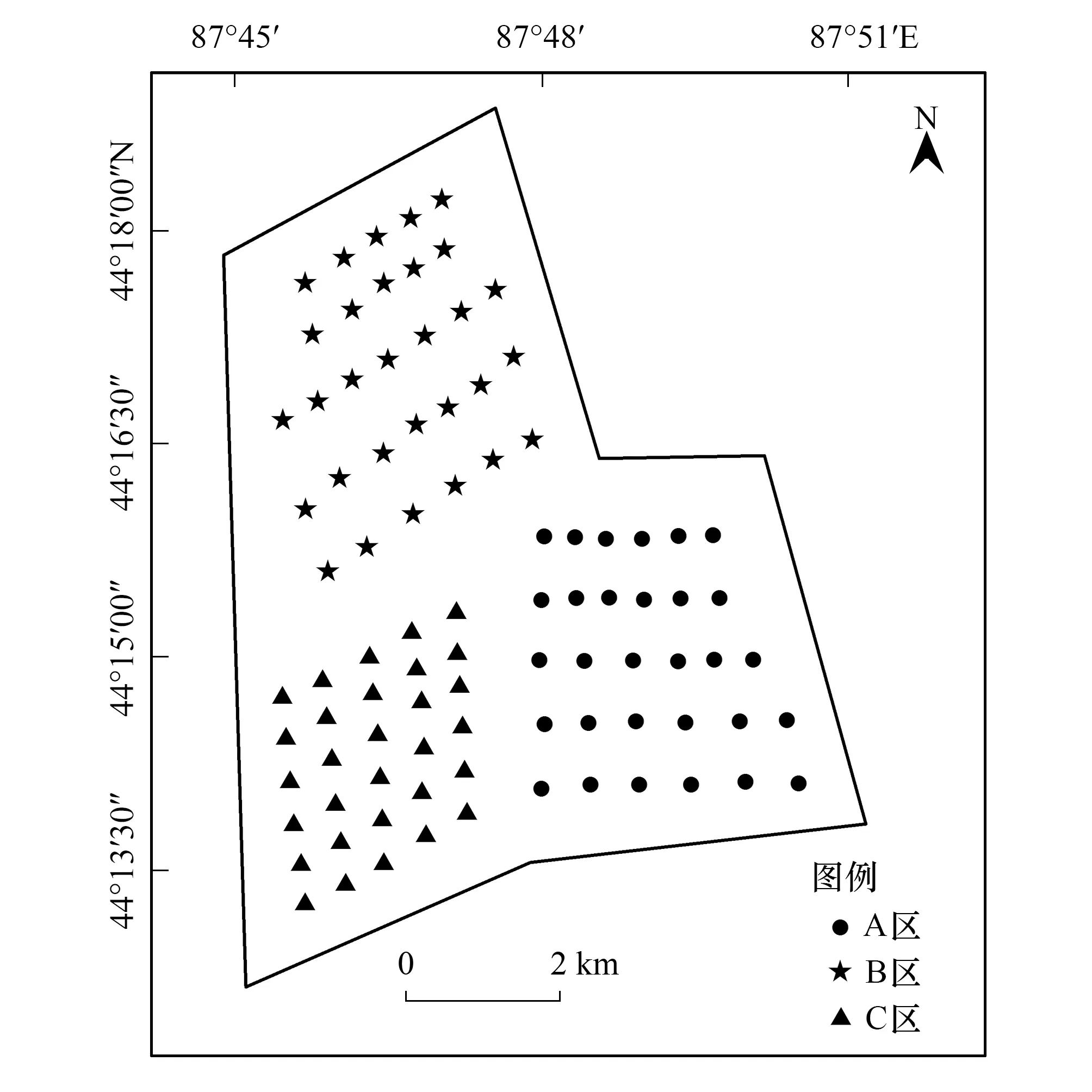
图1 研究区域位置及采样点分布图 Fig.1 Location map of the study area and distribution of the sampling sites
研究区位于天山北坡东段,准噶尔盆地南缘,地理位置为87°44′—88°46′E,43°29′—45°45′N,为典型的干旱荒漠区。该区气候属于中温带大陆性气候,冬季长干冷、严寒多雪,夏季短干热,春秋季节不明显,蒸发强烈,年均气温6.6℃,光照充足,热量丰富,温差大,降水稀少且空间分布不均,年降水量仅186mm,年蒸发潜力2064mm左右。土壤类型为灰漠土。
根据研究区土壤受人类活动的干扰程度,将其划分为3个区域(图1)。无人为干扰区(A区)几乎没有受到人为活动的干扰,基本保持景观的原有风貌,地表植被相对丰富,部分地点盖度更高、植株较大,有梭梭、琵琶柴、盐爪爪、白刺、红柳及成片的盐生杂草等,植被覆盖度约为30%,且整个区域有大量较厚且发育良好的黑色生物结皮;人为干扰区(B区)内主要为弃耕地,地表被犁翻耕且有很明显的骆驼踩踏痕迹。有猪毛菜及少量琵琶柴、梭梭、红柳、盐爪爪等植被,但植被覆盖度相对较低约15%—20%,区内土壤表面生物结皮较少,发育较差,部分地表无生物结皮,人为干扰较强烈;重度人为干扰区(C区)包含两片农场,受到强烈的人为干扰。土地全部被翻耕,人工种植的榆树林行间距均为3.5m,榆树林株距分别为3m和1.2m,平均高度为3m左右,最高的植株约4.3m,冠幅分别为0.5m×0.5m和1.1m×1.0m。3个区域相邻仅以栏网或沟渠相隔,整个研究区位于绿洲下缘的平原区,其地形、土壤属性、光照时长、热量分布、降水量、温度湿度等自然条件基本相似。因此,在干扰等级进行划分时,主要考虑的是土壤受人类活动的干扰程度。
虽然各区面积大小不同,根据野外实地考察情况,使得各区采样线间距设置有所差异,不能将其等分,但各区均采用网格法布设样点(图1)。这样就在各区形成可以全面控制该区土壤有机质变化情况的网格,以保证数据的代表性和合理性。A区位于研究区东部,由南向北布设5条采样线,每条采样线上分布6个样点;C区位于A区西侧,由南向北布设6条采样线,每条采样线上设置5个样点;B区位于C区北部,由南向北布设5条采样线,依据当地实际情况,每条采样线上设定5—7个样点,3个区域均设置30个采样点,每个样点间距保持在300—400m左右,尽可能均匀分布。
1.2 样品采集与处理
以Landsat系列遥感影像数据为参考,于2017年10月进行野外土壤样品采集。根据样点设置,按照一致性、同质性和代表性原则先选择10m×10m范围的植物样方,主要记录每个样方内植被种类、个体数,总盖度、高度以及土壤表层生物结皮生长情况,同时,详细记录每个样点周边环境特征。为使土壤样品代表性更强,先测完植被样方,然后在样点周围2m范围内以梅花桩方式采集5处土样混合均匀后放入密封袋中,封口标记编号,并用GPS定位。
将采集的土壤样品经过预处理之后送至中国科学院新疆生态与地理研究所理化测试中心,进行土壤有机质数据的测定。
1.3 数据处理方法与检验
采用4种方法对不同干扰程度下土壤有机质进行空间插值分析,并对不同插值法进行交叉验证,获得精度评价结果,得到基于最优插值方法的不同干扰程度下土壤有机质含量空间分布图。
1.3.1普通克里格(OK)空间插值法
普通克里格插值法(Ordinary Kriging)的适用条件是区域化变量具有空间相关性[24]。利用半变异函数,选取球状模型和高斯模型,来反映各区域变量的结构性和随机性。
1.3.2反距离加权(IDW)插值法
反距离加权插值(Inverse Distance Weighted)基于相近相似的原理:即两个物体的性质是否相似取决于两者距离的远近,离得越近性质越相似,反之,离得远则相似性小[25]。
1.3.3径向基函数(RBF)插值法
径向基函数(Radial Basis Function)插值法是一种精确的非线性计算工具[26]。每个点都能用几个高斯函数的叠加进行逼近[27],对于距离较远的点,其影响小于距离较近的点,这一特性排除了远距离点的干扰,使训练速度更快。
1.3.4局部多项式(LPI)插值法
局部多项式内插(Local Polynomial Interpolation)基于局部加权最小二乘法对处在特定重叠邻近区域内的多个多项式进行拟合的一种近似插值法[28]。
1.3.5插值结果的精度检验
插值的精度分析采用交叉验证的K折交叉验证(K-fold cross-validation),它是一种能快速评价插值结果质量的方法[29]。为更加准确地评估预测模型精度,采用最常用的十折交叉验证法,即将样本随机分成10份,轮流将其中的9份用于训练,剩余一份用于评估,循环10次后所有数据都会被验证一次,取10次结果的均值为最终预测误差。该方法的特点是可直接进行误差的估算无需任何要求,操作便捷、适用性强;尤其是数据量较小时计算效率会更高,数据的循环使用能更接近原始样本分布且不容易受到随机因素的影响。
评价指标采用决定系数(R2)平均预测误差(ME)和均方根预测误差(RMSE),依据R2越接近1、ME越接近0、RMSE越小其预测精度越高的原则,寻求最优插值方法。各指标计算公式如下:
(1)
(2)
(3)
式中,n为样本数,Xi为实测值,Xj为预测值。
2 结果与分析
2.1 不同干扰程度土壤有机质统计特征
从无人为干扰、人为干扰到重度人为干扰的梯度上,土壤有机质含量最大值、最小值、均值均逐渐减小,而标准差逐渐增大,即有机质含量逐渐减小(表1)。根据全国第二次土壤普查有机质分级标准[30],无人为干扰区处于四级中下等水平,人为干扰及重度人为干扰区均为五级缺乏水平。变异系数(CV)反映数据的离散程度,CV<10%为弱变异;10%≤CV≤100%为中等变异;CV>100%为强变异[31]。即无人为干扰区呈现弱变异,人为干扰及重度人为干扰区为中等变异。
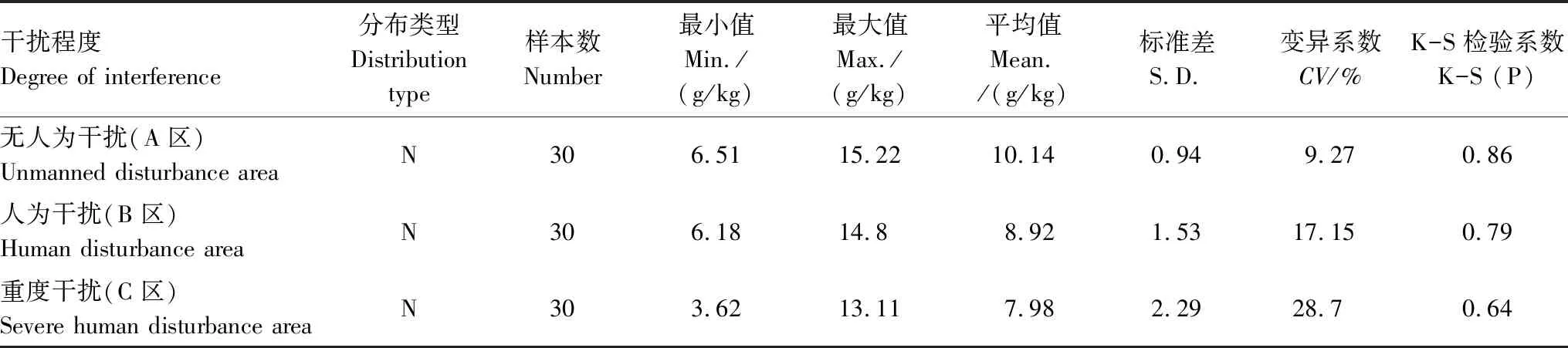
表1 不同干扰程度土壤有机质的描述性统计和K-S检验
N表示符合正态分布检验,标准差S.D.(Standard Deviation),变异系数CV(Coefficient of Variation),K-S检验(Kolmogorov-Smirnov)
2.2 不同干扰程度土壤有机质空间变异特征
利用地统计学方法对研究区不同干扰程度下土壤有机质进行模型拟合,比较各模型的决定系数(R2)和残差平方和(RSS),选取R2更接近1 且RSS较小的最优理论模型,得到模型相关参数值(表2)。随着干扰程度的加剧,R2逐渐减小,由0.932下降到0.764,减小了0.168;RSS逐渐增大,由0.027增大到1.24。无人为干扰区(A区)土壤有机质最优理论模型为球状模型,人为干扰区(B区)和重度人为干扰区(C区)为高斯模型。当块基比C0/(C0+C)<25%则以结构性变异为主,具有强烈的空间相关性;比值>75%表示其空间变异以随机性因素为主,空间相关性很弱;在25%—75%之间,则说明受结构性和随机性因素共同影响[32],空间相关性中等。无人为干扰区有机质块基比为12.26%,空间结构性极强,人为干扰区块基比为35.9%,空间相关性中等,而重度干扰区块基比为76.21%,说明在该区内土壤有机质含量的空间变异受随机性因素影响很大。
变程和分形维数(D)亦可反映区域化变量的空间自相关性大小及空间变异范围尺度,D值越小,由空间自相关部分引起的空间变异性越弱,结构性越好,受随机因素影响越小[33]。从无人为干扰区(A区)、人为干扰区(B区)到重度干扰区(C区),土壤有机质的变程和分形维数均在逐渐增大,说明随着人类活动力度的加大,随机因素对土壤有机质含量作用越来越强,空间自相关部分引起的空间变异性越高。可见,半方差函数充分反映了对不同程度人为干扰下土壤有机质的空间变异特点。

表2 不同干扰程度土壤有机质的半方差理论模型及其参数
S表示球状模型;G表示高斯模型;决定系数R2(Coefficient of determination),残差平方和RSS(Residual sum of squares),分形维数D(Dimension)
2.3 不同干扰程度土壤有机质空间插值结果的交叉验证
不同插值的交叉验证结果知(表3),各方法均有误差存在。A区土壤有机质的4种插值方法中,R2最大、RMSE最小,且ME最接近0的是OK法,其次是IDW法,而后为RBF法,LPI法插值能力相对较弱;而对B区和C区土壤有机质而言,各插值方法的精度分别为RBF法>IDW法>OK法>LPI法,RBF法>IDW法>LPI法>OK法,即RBF法能更精确地对B区及C区内土壤有机质含量进行空间插值分析。不同干扰程度下4种插值方法精度均表现为A区>B区>C区,其中OK法的R2变化范围较大,为0.312—0.625,且其对A区土壤有机质的插值精度最高(RMSE为2.049)。在B区和C区,OK法的插值精度相对变低,与A区相比较RMSE分别升高了0.482和1.033,R2分别下降了0.129和0.313;而RBF法和IDW法的RMSE较A区虽有所增大,R2虽有所减小,但其精度均高于OK法。可见,人为干扰程度的加剧对各插值方法的精度都会产生影响,这是因为不同强度的人类活动对土壤属性造成的干扰不同,使其理化特征发生改变,导致数据的离散程度各异,且各插值方法对不同区域内土壤理化性质变化的适用性有所差异。尤其是OK法的插值效果更易受随机因素左右,在人类干扰强度大,土壤属性变化强烈的区域进行插值是有一定局限的。
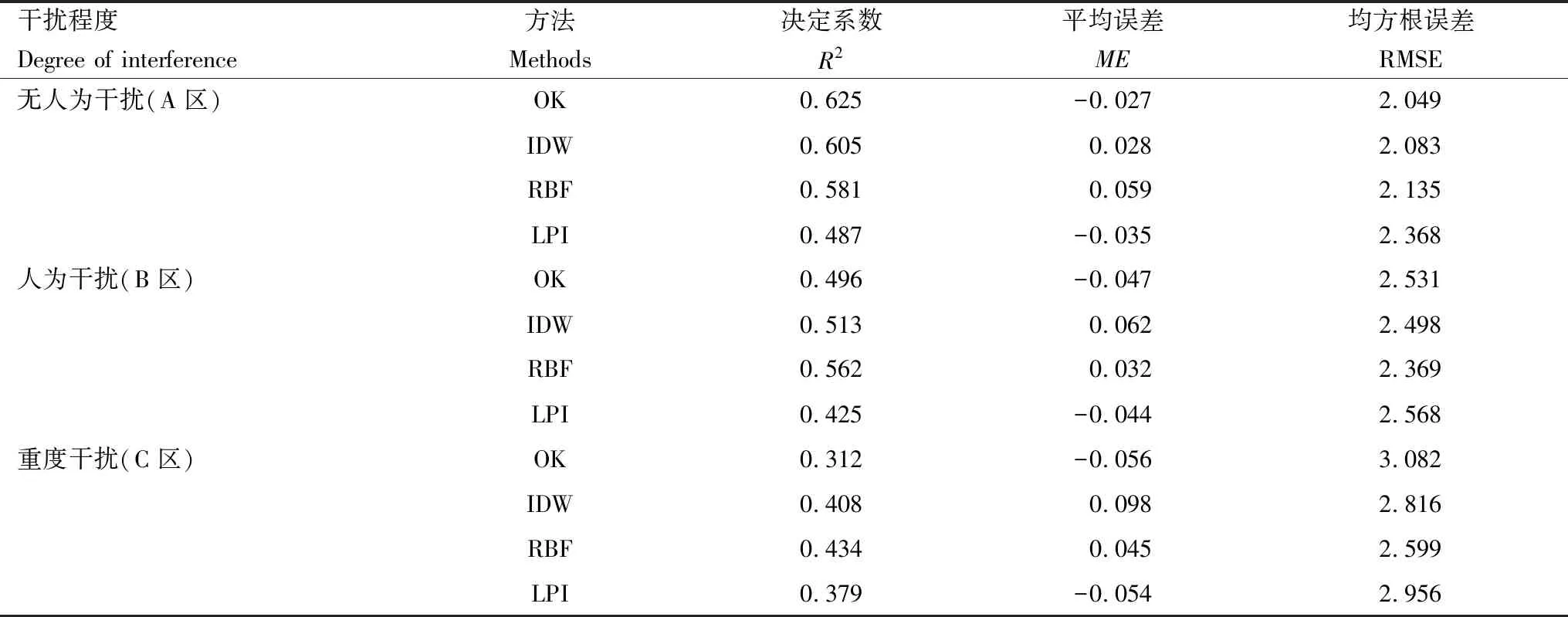
表3 不同干扰程度土壤有机质插值方法精度检验
普通克里金OK,反距离加权IDW,径向基函数RBF,局部多项式LPI,平均误差ME (Mean Error)
2.4 基于最优插值法土壤有机质的空间预测
利用各区域的最适插值方法:A区采用OK法、B区和C区采用RBF法,对不同干扰程度下土壤有机质进行空间预测,分析其空间分布特征(图2)。A区土壤有机质东部及东南部高,西部及东北部较低;B区中部及东部高,南部、西北部较低;C区在北部出现高值,中部及南部较低,且含量极值差距较大。可见,种植、翻耕、灌溉等人为因素对土壤有机质含量的分布格局有很大的影响,与近乎自然状态下的A区相比,B区和C区干扰程度不同,对土壤有机质分布特征产生的影响有所差异。这些分布特点与各区域土地利用类型、植被条件以及人类活动干扰程度等关系密切,A区以荒地为主,地表植被较丰富,几乎没有受到人为活动的干扰,从西至东有机质变化平缓;B区以半荒地、弃耕地为主,覆盖度相对较低,人为干扰具有随机性,有机质变化复杂;C区为弃耕地、人工林地,土壤全部被翻耕,人工林地种有梭梭林和榆树林,受人为干扰最强烈。
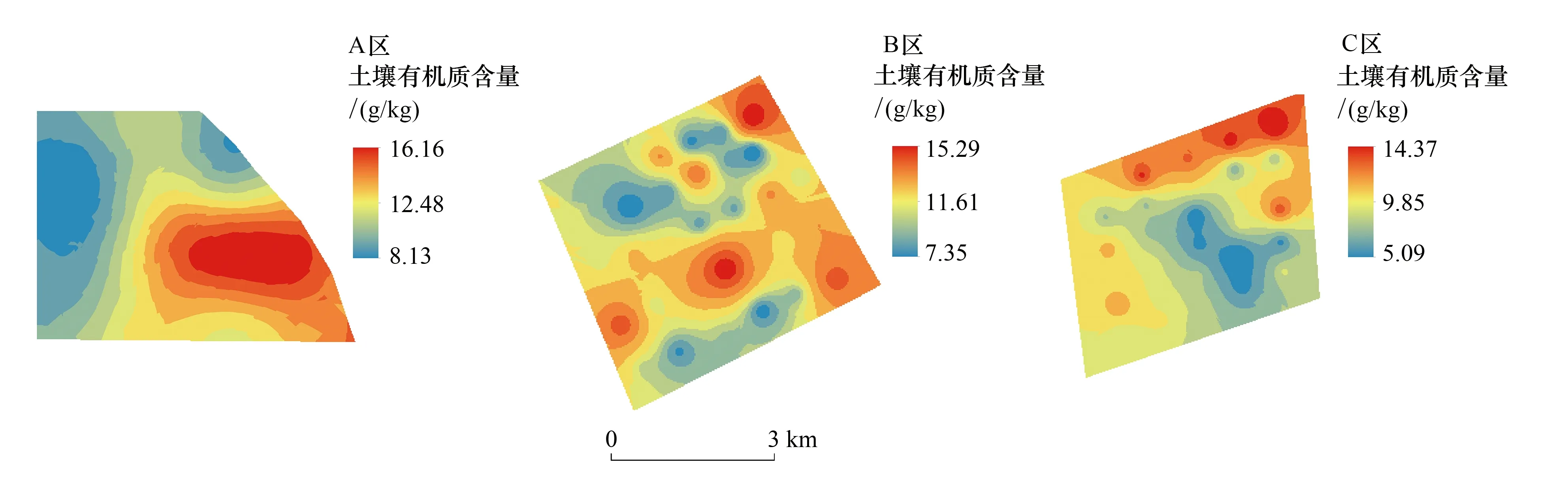
图2 不同干扰程度土壤有机质含量空间分布预测Fig.2 Prediction of spatial distribution of soil organic matter in different disturbance districts
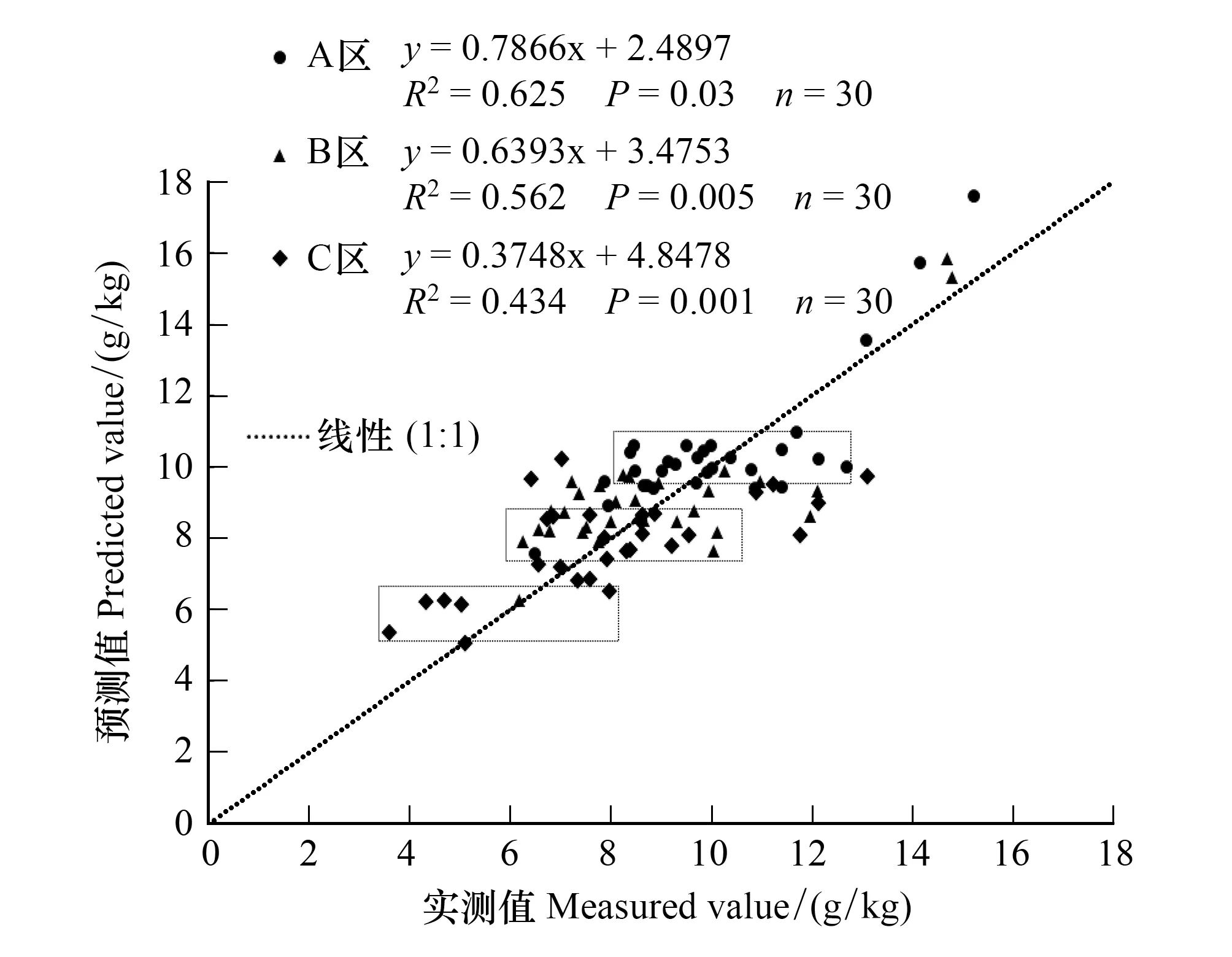
图3 基于最适插值方法土壤有机质预测值和实测值散点图Fig.3 Scatter plot of predicted values and measured values of soil organic matter based on optimal interpolation method
基于各区域最优空间预测模型,绘制出不同干扰程度下土壤有机质预测值和实测值的散点图(图3),分析数据较为均匀地布局在1∶1线的两侧,说明预测值和实测值总体上呈现出相对较好的线性关系。无人为干扰区有机质含量值相对较高,且数据分布较集中,而随人类干扰程度加剧,有机质值越低,且含量变化越大,分布越分散。
3 讨论
对于同一区域,采用不同的插值方法所得结果有所不同,同类插值方法在不同区域产生的效果亦会有差异。空间插值没有一个通用的、普适的模型,而是需要根据不同特征的研究对象来选择相对适宜的插值方法和相关参数[34]。
OK法多适用于具有强烈空间相关性的插值分析中,因为其空间插值精度一定程度上取决于待插值土壤属性的空间变异特征,这与前人研究结果一致[35-36]。OK法虽然取得了较好的成果[37-38],但对不同干扰程度下土壤有机质进行空间插值分析,并比较不同插值方法的精度,发现在样点数量不变的条件下(各区采样点均为30个),OK法仅对空间自相关性较强的、变异性较弱的无人为干扰区土壤有机质插值效果最好,而在人为干扰区插值精度偏低,在重度人为干扰区最低。主要是由于其首先考虑的是空间属性在空间位置上的变异分布,受人为干扰等随机因素导致空间变异性较高,仅依据样点间的地理位置信息对其进行插值必然会使其精度有所下降。因此,在不能充分满足克里格插值前提条件且土壤属性变化强烈的地区进行插值,会导致其精度偏低。同时,其算法较复杂,在选定变异函数时具有主观性。
RBF法适合于需要将样本值和拟合值保持一致的应用中,原因是它一定程度上能克服平滑效应,是一种精确的非线性插值方法,其结果会尽可能地保留元素含量的极值信息[39]。尤其是在数据较少,土壤有机质变异程度相对较大的情况下(人为干扰和重度人为干扰区)进行空间插值效果较好。同时,其最大的特点是能在高维空间中利用高斯函数[40],可以不受任何约束地逼近任意函数,而人为干扰区和重度人为干扰区土壤有机质的空间变异特征均符合高斯模型,因此,RBF法更胜一筹。
IDW法一般应用于对极值不要求度量的插值模型中,其算法相对简单,较易实现,适合分布较均匀且密集的样点。但选择函数幂次时具有敏感性,易受采样集群影响造成“牛眼”现象[41]。与OK法和RBF法相比,它基于相近相似原理,又不能对样本中的极大极小值进行预测,所以此法虽然能实现对各区域土壤有机质插值运算,但精度不如前两者高。而LPI法多适宜于解释小范围的局部变异,且平滑性较好的数据情况,因为它利用最小二乘法拟合元素含量的空间分布趋势,趋向于得到一个平滑的表面[42],且其平滑作用比其他3种方法更加明显。虽然它是一种非参数估计法,能消除异方差的影响[43],但其仅考虑样本局部范围趋势,针对特定空间领域内信息进行分析,所以不论在哪种情况下,LPI法的插值精度均不是最佳,其对各区域土壤有机质含量的插值分析局限性较大。
影响空间插值精度和效果的因素有很多,比如:环境背景、相关参数的选择以及采样点分布密度状况等。今后对土壤有机质的空间特征进行讨论时,应首先区别其是否受到人类活动的干扰,其次应详细区分其受人类干扰的强度,然后再对其分析研究。这样更有利于寻求不同干扰情况下土壤属性的最优插值方法,而后才能更加精准地进行空间分析。
4 结论
不同干扰程度下土壤有机质均呈正态分布,且无人为干扰区有机质具有弱变异性和强烈的空间自相关性,人为干扰区空间变异及相关性均呈中等强度,重度人为干扰区为中等变异,而空间相关性较弱。土壤有机质含量受人为干扰活动等随机因素作用越强,空间自相关部分引起的空间变异性越高。
随着干扰程度加剧,无论采用哪种方法对土壤有机质空间插值分析,其精度均在降低。从无人为干扰区到人为干扰区再至重度干扰区,各种方法的插值精度R2由0.487—0.625降低为0.425—0.562再降至0.312—0.434。其中OK法一定程度上依赖于有机质的空间变异特征,在空间结构性强的无人为干扰区,其插值精度最高;而在人为干扰和重度人为干扰区插值效果最好的是RBF法。

