基于模糊混合退火分布的多目标高斯混合粒子PHD滤波算法*

冉星浩，陶建锋，贺思三

(空军工程大学防空反导学院， 西安 710051)

0 引言

目标跟踪在民用以及军事层面均有普遍性的运用，例如飞机和船舶跟踪等。这其中，多目标跟踪问题更是当前世界上讨论的关键问题[1-2]。然而在杂波环境下，多目标跟踪与单目标跟踪相比难度较大[3]。

2000年Mahler在随机有限集理论的基础上，提出了基于随机有限集的概率假设密度的滤波方法(PHD)来解决多目标跟踪问题[4]，相比于传统的关联算法，PHD算法不仅避免了复杂的数据关联过程，同时跟踪精度和实时性更高。

PHD算法目前可以分为两种：一种是高斯混合PHD(GM-PHD)[5]，这种算法使用的噪声模型为高斯模型，受限于噪声模型，同时会出现计算精度较低的问题；另一种是粒子PHD算法(PF-PHD)，可以适用于非线性非高斯情况下[6]，不受噪声模型限制同时精度较高，但是计算量较大，会出现滤波发散的情况使得跟踪效果往往达不到要求。

为了解决以上问题，文献[7]提出了高斯混合粒子PHD(GMP-PHD)滤波方法，这种方法综合了以上两种PHD算法优点，然而这种方法在进行重要性采样时没有考虑最新的量测信息，使得采样的样本与真实的后验概率所得到的样本偏差较大，影响滤波效果。

针对以上问题，文中在高斯混合粒子PHD基础上，提出基于模糊混合退火分布[8]的改进高斯混合粒子PHD算法 (I-GMP-PHD)。该算法在高斯混合粒子PHD滤波的基础上，采用状态变量分解和通过模糊系统引入退火因子的方法产生最优的建议分布函数，这样得到的重要性密度函数[9]融入了最新的量测信息，同时克服了转移先验概率密度存在的问题。仿真结果表明该算法相比于传统算法，大大提高了滤波精度和系统稳定性。

1 算法原理

1.1 标准粒子滤波算法

粒子滤波算法起源于蒙特卡罗思想，通过粒子集来近似目标的后验概率密度函数，适用于任何形式的状态模型[10]。其实质是通过对重要性密度函数采样得到一组随机样本来近似目标后验概率密度函数，得到的样本称为粒子[11]，然后计算粒子权值，用粒子和权值加权得到样本均值代替贝叶斯估计中的积分运算得到目标状态估计[12]。

1.2 模糊混合退火粒子滤波算法

针对粒子滤波出现的粒子退化问题，混合退火粒子滤波由于分别采用转移先验和融入了最新量测信息的后验概率密度作为建议分布进行采样，融合了两者的优点而受到广泛关注。但是由于是利用先验分布来得到表征状态的粒子，混合建议分布存在与似然分布偏差较大的问题。针对以上问题，再利用状态噪声和量测噪声统计特性之间的关系，引入退火因子[13]来解决。

1.2.1 混合退火建议分布

(1)

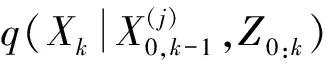
(2)

式(2)详细推导见文献[10]附录。其中退火参数β范围为0≤β≤2，选择原则为：

1) 若Σd<Σv，此时先验分布大部分处于似然函数平坦区外，取0<β<1使得先验函数更为平坦；

2)若Σd≈Σv，此时先验分布与似然函数大部分重合，取β=1，即采用先验分布作为建议分布，滤波性能更好；

3)若Σd>Σv，此时先验分布相比于似然函数尖峰来说较平坦，取1<β<2，使先验分布形状变尖锐，即采用似然函数为建议分布。

1.2.2 模糊推理系统

在传统的混合退火建议分布中，概率密度分布存在不确定性，然而退火参数β的取值固定，从而影响粒子滤波效果。为了解决这个问题，通过引入模糊推理系统FIS(fuzzy inference system)，对传统的混合退火粒子滤波算法进行改进，利用模糊系统依据输入变化特征做出不同的决策，进行输出，得到模糊混合退火粒子滤波算法(FAHAPF)。

定义调节b：

(3)

退火参数β取值由b进行调节。

定义模糊子集equal为在1附近，more代表基本<1，less代表基本>1，β的FIS规则为：

(4)

其中，β和b的隶属度函数如图1和图2所示。

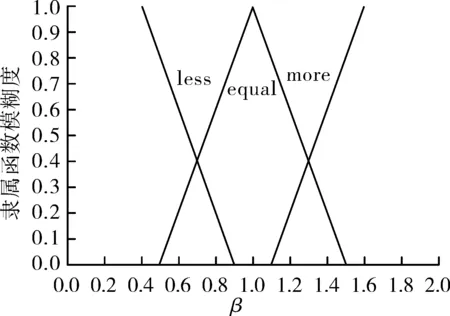
图1 β的隶属度

图2 b的隶属度

1.2.3 模糊混合退火粒子滤波算法

混合退火粒子滤波算法步骤如下：

1)初始化：首先对状态向量进行分解，通过以上FIS确定退火因子β并设计建议分布；

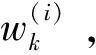
4)状态估计:在已知q(xk|z1,k)的情况下，估计系统状态及误差：

(5)

(6)

(5)令k=k+1，返回步骤2)。

2 PHD滤波算法

2.1 PHD滤波原理

PHD滤波分为预测和更新[14]两步：

1)预测

(7)

2)更新

(8)

式中：βk|k-1(xk|xk-1)为衍生目标的强度，γk(xk)为新出生目标的PHD，ek|k-1(xk-1)fk|k-1(xk|xk-1)为存活目标的强度，ek|k-1(xk-1)为目标存活概率，fk|k-1(xk|xk-1)是目标的状态转移概率；PD(xk)为检测概率，g(z|xk)为目标似然函数，κk(z)为杂波强度。

2.2 GMP-PHD滤波

传统的高斯混合粒子PHD滤波利用一组高斯项相加来近似目标的概率分布[15]，分为预测和更新两步。

1)预测

Dk|k-1(x)=Ds,k|k-1(x)+Dβ,k(x)

(9)

(10)

(11)

对高斯项采样得：

(12)

式中：

(13)

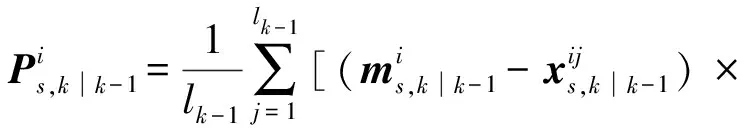
(14)

化简可得：

(15)

2)更新

GMP-PHD滤波中似然函数为：

g(z|x)=N(z;h(x),R)

(16)

更新方程为：

(17)

(18)

(19)

(20)

(21)

GMP-PHD算法综合了两种PHD算法的优点，但是由于在重要性采样过程中没有考虑到量测值，导致与真实值存在偏差从而出现精度不高、滤波发散等问题[16]，这样对于要求比较高的系统，算法达不到预期的要求。因此，提出了改进的I-GMP-PHD(improved GMP-PHD)算法。

2.3 改进I-GMP-PHD算法步骤

结合FAHAPF算法和上述GMP-PHD滤波方法，改进I-GMP-PHD算法的步骤描述如下：

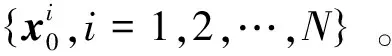
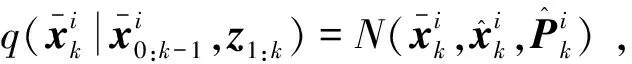
3)粒子的预测和更新：采样后根据样本状态和权值进行预测，再利用量测值对预测值进行更新，步骤如下:

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

4)权值递推：

(32)

(33)

5)PHD的预测与更新：

Dk|k-1(x)=Ds,k|k-1(x)+Dβ,k(x)

(34)

式中：

(35)

(36)

化简可得：

(37)

PHD更新为：

(38)

权值更新为：

(39)

6)目标个数估计和更新：

(40)

(41)

3 仿真结果与分析

为了验证改进算法优越性，分别用GMP-PHD、和I-GMP-PHD算法的性能进行对比分析。

3.1 仿真环境

仿真设定为二维平面区域中，跟踪目标数目未知且变化的多目标跟踪例子。目标跟踪模型为：

xk+1=Fxk+Gwk

(42)

(43)

(44)

(45)

上述式中，xk包括目标的位置与速度。

仿真中共有5个目标，设定初始时刻存在一个目标，初始状态为(-40,3,40,-1),之后有4个目标交替出现。目标以w=0.025 rad/s做曲线运动，各个目标之间运动轨迹有交叉，假设目标存活概率与检测概率均为0.99。wk是标准差方差为0.01的高斯白噪声；vk为量测噪声，方位角误差方差为0.01 rad2，距离误差方差为0.1。采样周期为1 s，仿真时间为100 s。采取最优子模型分配距离(optimal subpattern assignment,OSPA)作为多目标跟踪性能的评价标准。

3.2 仿真结果分析

根据设定的仿真环境，分别用两种算法对5个目标进行跟踪，结果如图3～图7所示。

图3 目标真实航迹

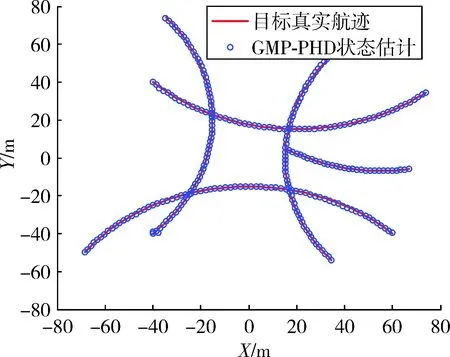
图4 GMP-PHD状态估计图

图5 I-GMP-PHD状态估计图

图3为杂波环境下目标真实轨迹图，图4、图5和图6分别是GMP-PHD算法，I-GMP-PHD算法的跟踪效果对比图与OSPA距离对比图。从图4和图5可以看出两种算法都能较好地跟踪多个目标，但是从图6可以看出I-GMP-PHD跟踪多目标OSPA距离小于GMP-PHD，跟踪精度要高于GMP-PHD。这是因为改进算法采取模糊混合退火分布产生最优的建议分布，充分考虑了量测值，同时引入了退火因子克服了转移先验分布存在的问题，解决了粒子退化问题，滤波效果更佳，大大提高了跟踪精度，跟踪误差更小。

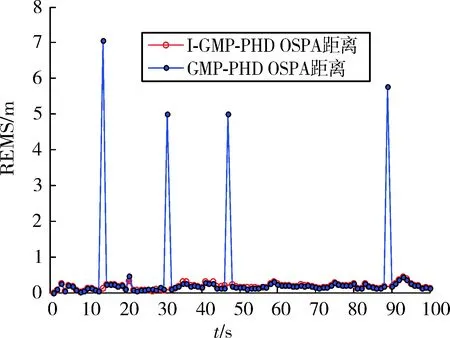
图6 OSPA距离对比图

图7 目标个数估计

同时从图7看出两种算法对目标个数估计与真实的目标个数大致相同，但是GMP-PHD算法对目标个数估计存在较大误差，而I-GMP-PHD算法对目标个数估计更加精确。

4 结论

文中从高斯混合粒子PHD滤波算法中存在的跟踪精度不高和滤波发散问题出发，提出了一种基于模糊混合退火分布的多目标高斯混合粒子PHD算法。首先利用模糊推理系统确定调节因子调节退火系数，然后设计改进的混合退火分布产生重要性密度函数融入GMP-PHD滤波框架中，再进行PHD更新。仿真结果表明，改进算法能够有效地跟踪多个目标，相比于GMP-PHD滤波算法，跟踪精度大大提高，系统稳定性也得到进一步加强。